Keywords

1 Introduction

Coronavirus disease (Covid-19) occurred first in Wuhan city of Hubei province of China in December 2019. The World Health Organization (WHO) has declared the spread or transmission of this virus as a global pandemic [1,2,3,4]. Initially, it has proposed that the transmission of the coronavirus is related to a seafood market (Wuhan Seafood Wholesale Market), and exposure took place whoever visited that market. Coronavirus genomic infection-2019 has been announced as a severe health emergency arising international awareness due to its spread to 201 countries at present. In April of the year 2020, it has undoubtedly been called the pandemic outbreak having approximately 11,16,643 infections confirmed, leading to around 59,170 deaths recorded all over the world. In general, human-affecting coronavirus contagions has some similarities with two Beta coronaviruses: severe-acute-respiratory-syndrome-coronavirus (SARS-CoV) and Middle-East-respiratory-syndrome-coronavirus (MERS-CoV) [5, 6].

In December 2019, the succession of pneumonia cases from an unknown cause appeared across the city of Wuhan, China, and clinical tests detected them as viral pneumonia. Deep-sequencing-analyzers depicted that the lower respiratory-tract samples indicated a novel-coronavirus coined as a 2019 novel coronavirus (2019-nCov). As of now, around 800 confirmed cases found among health-care workers from this genomic viral which exists in Wuhan along with the exported population in other provinces of China, Thailand, Japan, South Korea & the USA. The clinical findings, such as lower and upper respiratory symptoms of the infection, have been reported based on research findings from several countries. The pandemic situation has worsened at the national as well as at the international level. The outbreak of coronavirus (Covid-19) is categorized as incidence representing number of confirmed new cases, number of cases recovered and number of deaths occurred. Looking towards the daily outbreak of this virus and suspecting its transmission through contact of humans, various countermeasures such as social distancing and lockdown implemented to prevent its potential spread. Therefore, tasks about effective control of outbreak motivated us to develop a reasonable and feasible epidemic model for this infectious disease. Infectious disease epidemiology is characterized by the presence of at least one active player in addition to human population, namely, the infectious agent or parasite [7, 8]. The presence of this additional propagating population sets the stage for aspects specific to infectious disease epidemiology. First and foremost is transmission. Transmission from one host to another is fundamental to the survival strategy of the infectious agent, since any host will eventually either clear the infection or die, even if from an unrelated cause. A consequence of transmission is that, unlike non-infectious diseases, the occurrence of infectious diseases in individuals depends on the occurrence of those diseases in other members of the population. Sir Ronald Ross [9] called this dependence of disease events in infectious diseases as “dependent happenings”.

Although most methods used in general epidemiology are applicable to the study of the infectious diseases, additional concepts are needed to describe the phenomena resulting from the dependence of disease events. These include infectiousness, the transmission probability, contact patterns and the basic reproduction number (R0). An intervention in infectious diseases can also have several different kinds of effects, including direct effects on a person receiving the intervention as well as indirect effects on other individuals. These different effects require additional parameters and study designs for their evaluation. Exposure to infection plays a special role because exposure to infection is necessary for infection and disease to occur. The components of exposure to infection, such as the contact and mixing patterns of the infective and susceptible hosts, as well as the degree and duration of the infectiousness, need to be taken into account in infectious disease epidemiology.

Even when conventional epidemiologic concepts are applicable, these should be used in infectious disease studies only after close examination of the underlying assumptions. Because the temporal evolution of the host population and the disease process under study can be quite rapid compared with the time frame of the study, conventional epidemiologic methods that assume stationarity can produce very biased estimates of effects in infectious disease epidemiology. Epidemiology of infectious disease is an extension of ecology and evolution. Since each infectious agent has its own life cycle, immunology, ecology, evolution and molecular biology, thus studies of infectious disease require the understanding of all these aspects [10]. Since present circumstances focus on the possibility of the spread of coronavirus, we have developed an epidemiological model named RD-Covid-19. With the help of the numerical simulation of RD-Covid-19 Model, the outburst for Covid-19 cases in several countries like China, India, Brazil and Russia has been simulated. RD Model provides the knowledge of basic reproduction number, R0, and with the help of R0, the rate of severity of the coronavirus disease in above mentioned countries has explored. Herd immunity computed from R0. Case fatality rate (CFR) is an additional component of the epidemiology of infectious disease [10, 11], which was calculated using the RD-Covid-19 model. Modelling of the novel Coronavirus outbreak using data based transformations for epidemiology has been forecasted [12]. A Multi-risk SIR model with optimally targeted lockdown analyzed for the estimation of the transmission risk of 2019-nCov and its implication on public health interventions [13,14,15]. The corona theorem for differrnt functions analyzed and applied to study the spectral problems for predictive modelling [16, 17]. Predictive models for small molecules that target the severe acute respiratory syndrome human coronavirus nowcasted and forecasted for international spread of 2019-nCov [18, 19]. The clinical implications of Glycopeptide antibiotics that would inhibit Cathepsin L in the Late Endosome/Lysosome, and blocks entry of Ebola virus, MERS-CoV and SARS-CoV-2 discussed [20, 21].

The outburst of Covid-19 studied in detail through data-based modeling & forecast analysis with a detailed explanation of the mathematical perspective to understand the spread of infectious diseases [22, 23]. Estimation and spread of atmospheric pollutants through dynamic indicators, statistical simulations were modeled and analyzed in detail for prediction and forecasting [24,25,26,27,28,29,30]. Coronavirus data analyzed for forecasting and risk assessment [31]. Transmission dynamics using data analysis of the Covid-19 outbreak discussed for government interventaions and tracking the rate of transmission of the epidemic, dynamics of transmission and its control [32,33,34,35,36,37]. For 2019-nCoV pandemic, the efficiency of control strategies towards the reduction of social mixing and complexity with futuristic estimations for China modelled using supervised learning [38]. Time series forecasting of the spread of genomic virus using genetic programming for study of pandemic outbreak based on training testing of multimodal data predicted [39,40,41]. The molecules that enter into host cell and cause acute respiratory syndrome targeting towards coronavirus forecasted impending Covid-19 spread cases for China and some other regions using mathematical & traditional time-series prediction models [42,43,44].

In this chapter, we introduce a few important concepts of infectious disease epidemiology, focusing on the consequences of the dependent structure of disease events for measures of the effect. The detailed structure of RD-Covid-19 model with its numerical simulation also presented. Section 2 presents the various components of epidemiology of infectious disease such as time lines of infection, transmission probability, and secondary attack rate. Section 3 describes the basic reproduction number and its estimation methodologies. Incidence rate as a function of prevalence and contact rate is presented in Sect. 4. Section 5 describes the dynamic epidemic process in a closed population. Section 6 describes our RD-Covid-19 model and its various components (network). Numerical simulation of our model for countries, as mentioned, is presented in Sect. 7. Section 8 concludes the chapter with possible future research in this direction.

2 Infectious Disease Epidemiology Components

Its various components always understand the epidemiology of an infectious disease. These are (1) timelines of infection, (2) transmission probability, and (3) secondary attack rate. This section presents insight into these components.

2.1 Timelines of Infection

The time lines of infection within the host can be best described with reference to the dynamics of infectiousness and of disease (Fig. 1). Both start with the active disease of the vulnerable host by the parasite. The time line of infectiousness includes the latent period, the time interval from infection to development of infectiousness and the period of infectiousness of the host, during which time the host could infect another host. Eventually, the host becomes noninfectious either by recovery from the infection, possibly developing immunity, or by death. The host can also become noninfectious while still alive and still harboring the parasite.

Fig. 1
figure 1

Timeline for infection and disease

Full size image

The time line of disease within the host includes the incubation period, the time from infection to development of symptomatic disease and the symptomatic period. The probability of developing symptoms or disease after becoming infected is the pathogenicity of the interaction of the parasite with the host. Eventually, the host leaves the symptomatic state either by recovering from the symptoms or by death. The host becomes an infectious carrier if he recovers from symptoms but remains infectious. The terminology used in infectious disease epidemiology always differs from that of non-infectious disease epidemiology. The term latent period refers the time corresponding to the period from development of asymptomatic disease to development of symptoms. The incubation period in infectious disease is a combination of what are called the induction and the latent periods in noninfectious diseases. The configuration of the two time lines in Fig. 1 and their relation to one another are specific to each parasite and can have important public health consequences and implications for study design.

2.2 Estimation of Transmission Probability

Transmission probability is an important parameter of infectious disease epidemiology which is defined as the probability that, given contact between two infective source and a susceptible host, successful transfer of the parasite will occur so that the susceptible host becomes infected (Fig. 2). Hence, estimation of transmission probability is very important from the point of knowing the outbreak of infectious disease Covid-19. The transmission probability depends on characteristics of the infective source, the parasite, the susceptible host and the type of definition of contact. The infectious source could be another person, as in Covid-19. The mode of transmission of a parasite determines what type of contact is potentially infectious.

Fig. 2
figure 2

Transmission from an infective to a susceptible host during contact

Full size image

It is worth to know the method of estimating transmission probability. In one method, infectious individuals are identified and the proportion of contacts that they make with susceptible hosts that result in transmission is determined. This approach can be explained further by introducing secondary attack rate.

Secondary Attack rate:

The conventional secondary attack rate (SAR) defined as the probability of the occurrence of disease among known susceptible persons following contact with a primary case:

$$SAR = ~\frac{{n~\left( {number~\,of\,~persons~\,exposed~\,who\,~develop~\,disease} \right)}}{{m~\left( {total~\,number~\,of\,~susceptible~\,exposed\,~persons} \right)}}$$

2.3 The SAR is a Proportion, Not a Rate

In another technique, susceptible hosts are identified and data gathered on the number of contacts they make with infectives and outcomes of their infection. In this method binomial model is used to estimate the transmission probability. The probability of transmission during a contact between a susceptible and an infectious person is denoted by ‘p’ and the probability of a susceptible person’s escaping infection during the contact is ‘q = 1 – p'. The probability of escaping infection from all n potentially infective contacts is \( q^{n} = \left( {1 - p} \right)^{n.} .\) The probability of being infected after n contacts, that is, of not escaping infection from all n contacts is \( 1 - q^{n} = 1 - \left( {1 - p} \right)^{n} .\) The maximum likelihood estimate of the transmission probability under the binomial model can be written as

$$ p = \frac{{number \, of \, susceptibles \, who \, become \, infected}}{{total \, number \, of \, contacts \, with \, infectives}}$$

It is required to note that, in the binomial model, the total number of potentially infectious contacts that susceptible individuals make, while in SAR, each vulnerable person had just one potentially infectious contact with the infective.

3 Estimation of Basic Reproduction Number/ Proliferation Number

Basic reproduction number, R0 is defined as the expected number of new infectious hosts that one infectious host will produce during his or her period of infectiousness in a large population that is completely susceptible. R0 does not include the new cases produced by the secondary cases which do not become infectious. For example, if R0 = 9 for some infectious disease in a population, then one person with that infectious disease introduced to that population would be expected to produce nine new secondary infectious cases before recovering, if the population were completely susceptible. If the person produced two additional cases which did not become infectious, R0 would still be 9. In general, for an epidemic to occur in a susceptible population, R0 must be greater than one. If R0 < 1, an average case will not produce itself, so an epidemic will not spread. Since R0 is an average, it is possible that a particular infectious person will produce more than one infective case, even when R0 < 1, so there may be a small cluster of cases. We would not, however, expect a self-sustaining outbreak.

The basic reproduction number, R0 for infectious disease depends on three parameters, which are: (a) the rate of contacts c, (b) the duration of infectiousness d, and (c) the transmission probability per potentially infective contact p. Mathematical expression of R0 hence can be written as

$$ R_{0} = \frac{{number of contacts }}{{time}} \times \frac{{transmission probability}}{{number of contacts}} \times duration\left( {time} \right) = cpd $$

By definition, R0 assumes that all contacts are with susceptibles. Under these conditions, the expected number of new cases produced by an infectious person is less than R0 and is called the effective reproductive number, R. If x is the proportion of a randomly mixing, homogeneous population that is susceptible, R is the product of R0 times the proportion x of the contacts that are with susceptibles. So, R = R0 x. For example, if R0 = 9 and x = 0.5, then R = 4.5. So an infectious disease would produce on average only 4.5 new secondary cases in this population. We can also write R = R0 (1 – f), where fraction f is immunized before the age of first infection and (1 – f) would be the maximum fraction of the population that is susceptible, disregarding immunity from previous disease. Therefore, to eliminate transmission, we should have, R = R0 (1 – f) < 1. Therefore the fraction that needs to be immunized to eliminate transmission is f > 1 – 1/R0. A higher R0 requires immunization of a higher fraction to eliminate transmission.

Herd immunity [11] describes the collective immunologic status of a population of hosts, as opposed to an individual organism, with respect to a given parasite [9]. Herd immunity of a population may be high if many people have been immunized or have recovered from infection with immunity or may be low if most people are susceptible. As herd immunity increases, R will decrease.

3.1 Estimation of R0

If the average life expectancy, L in a population is known, then R0 can be estimated from the relation, R0 = L/A, where A = 1/I (incidence rate). R0 can be calculated by computing the ratio of the rate of infection (β) to the rate of recovery (γ) for a standard SIR epidemic model. Maximum likelihood method can be the alternate method for estimating R0. In case of a standard compartment epidemic model or networked model, R0 is computed by next generation matrix method, where maximum eigenvalue of the next generation matrix is the value R0.

3.2 Virulence of R0 and the Case Fatality Ratio (CFR)

Virulence is a measure of the spread with which a virus (coronavirus) kills an infected host. Since R0 is a function of the time spent in the infective state, R0 could decrease as virulence increases. The case fatality ratio (CFR) is the probability of dying from a disease (Covid-19) before recovering or dying or something else [11]. Mathematically, CFR is defined as the ratio of number of deaths due to disease to the number of confirmed infectious cases. As virulence increases, the CFR increases.

4 Incidence Rate as a Function of Prevalence and Contact Rate

Apart from R0, transmission probability, the incidence rate, also used in infectious disease epidemiology. Under the assumption of simple random mixing, constant contact rate, c, and the transmission probability p, the incidence rate I(t) expressed as a function of the prevalence P(t) at time t of infectious persons defined as

$$ I \left( t \right) = cpP\left( t \right) = \frac{{R_{0} }}{d}P\left( t \right) $$
(1)

5 Dynamic Epidemic Process in a Closed Population

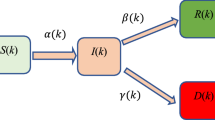
If the population is closed, then there are no births, immigration, deaths, or emigration. In a typical cohort study, we would not necessarily be concerned with how the individual people interact. In any study of infectious disease, the underlying contact and transmission process is essential, so we need to think about these processes in our model. If S is the susceptible population, I, the infected population, and R is the recovered population, we can have a SIR epidemic model [44,45,46,47] governed by following network diagram (Fig. 3) and equations as presented in Eq. (2).

Fig. 3
figure 3

Network diagram of SIR Model

Full size image
$$ \left. {\begin{array}{*{20}c} {\frac{{dS}}{{dt}} = - \beta \frac{{SI}}{N} } \\ { } \\ { \frac{{ dI}}{{dt}} = \beta \frac{{SI}}{N} - \upgamma{\text{I}} } \\ {\frac{{dR}}{{dt}} = \upgamma{\text{I}} } \\ \end{array} } \right\} $$
(2)

where, β denotes the infection rate, γ indicates the rate of recovery and the total population is N = S + I + R.

The dynamics of the epidemic described by Eq. (2) The rate at which people leave the susceptible compartment S and become infected is simply the incidence rate. Prevalence of infectives at time t, P(t) is the number of infectious people I(t) divided by the size of population N, or I(t)/N. The incidence as a function of prevalence is given by

$$ \begin{aligned} Incidence\left( t \right) & = cpP\left( t \right) = cp\frac{{I\left( t \right)}}{N} \\ \frac{{dS}}{{dt}} & = - Incidence\left( t \right)S\left( t \right) = - cp\frac{{I\left( t \right)}}{N}S\left( t \right) = - \beta \frac{{SI}}{N} \\ \end{aligned}$$

Therefore, the infection rate is given by β = c p. A cross-sectional study to estimate prevalence P(t) of current infection would yield an estimate of I(t)/N. We can write the differential equation representing the variation of the infected population for a variety of susceptible population of SIR model (Eq. 2) can be written as

$$\frac{{dI}}{{dS}} = \frac{\gamma }{\beta }\frac{N}{S} - 1$$
(3)

Similarly, we can also write,

$$\frac{{dI}}{{dR}} = \frac{{\beta SI}}{N} - 1$$
(4)

Analytical solution of Eq. (3) with initial condition S(0) = N, I(0) = 0 and R(0) = 0 can be written as

$$I = f\left( S \right) = \frac{{N\gamma }}{\beta }ln\left( {\frac{S}{N}} \right) + \left( {N - S} \right)$$
(5)

Equation (5) utilized to reconstruct the phase of the infected-susceptible population. The epidemic process also depends on population biology. By using definition of R0, for SIR model we can easily express R0 = c p/γ = β/γ. The expected number of new cases per infective host decreases from R0 to R = R0 (S/N). The epidemic peaks begins to decrease when R < 1, so that S(t)/N < 1/R0, that is, when the proportion of the population still susceptible becomes less than the reciprocal of the basic reproductive number. If an intervention (social distancing and lockdown) reduced some aspect of R0, then the intervention would result in the epidemic peaking when a higher proportion of the population was still susceptible, and fewer people would become infected before the epidemic died out.

6 RD-Covid-19 Epidemiological Model

Looking towards the need of an epidemiological forecasting model for knowing the outbreak of coronavirus we have developed a hybrid model RD-Covid-19 which is a networked model of a data-driven logistic model, SIR model, SEIR model [43,44,45,46,47,48] and SEIQRDP (Susceptible, Exposed, Infected, Quarantine, Recovered, Dead, Protected) model. Epidemiological models are generally dynamic model and data dependency. Hence, forecasting the spread of the coronavirus disease (Covid-19) will change with the change or availability of new datasets addressing confirmed, recovered, and death cases. Moreover, every epidemiological model is the compartmental model, and the introduction of a fresh compartment always based on certain assumptions. The assumption based modeling motivates us to develop a data-independent epidemiological model to forecast the coronavirus outbreak optimally. Accordingly, this demands to develop an optimal model to predict the spread or transmission of Covid-19 optimally. Therefore, with a view to this demand, we developed a hybrid model by the networking of logistic Model with SIR, SEIR, and SEIQRDP Model [47, 48]. The fundamental concept behind this networked model is to cascade the output of one model into the input of another model. Every model in this work is calibrated with the help of the available data in a sense, that parameters of the specific model at every stage are estimated using nonlinear least square optimization method.

In the cascade, at first parameters (infection rate and rate of recovery) of a data-driven model (logistic model) are estimated. Estimated values of these parameters used as guess value of the parameters of the SIR model, which calibrated further using the same data set and generate an improved amount of rate of infection and rate of recovery parameters of the SIR model. In the next stage, again, those values are used as input to the SEIR model. It is considered that, at the input stage, values of the parameters of the model accepted as guess value. Finally, the estimated values of the parameters by fitting the SEIR model along with the other parameters of the SEIQRDP model used as a guess value (input) of the SEIQRDP epidemiological model. Finally, the Model SEIQRDP numerically solved with the fitted values of the model parameters. Since the estimated values of the rate of infection and rate of recovery are going through several stages for their improvement, our model provides optimal values of the rate of infection and rate of recovery. These two parameters of a dynamic epidemiological model are data-dependent. Other parameters, such as incubation rate, protection rate, and quarantine period, guessed based on model assumptions. Assumptions of SIR model are:

  1. (1)

    The only way a person can leave the susceptible group is to become infected.

  2. (2)

    The only way a person can leave the infected group is to recover from the disease.

  3. (3)

    Once a person has recovered, the person received immunity.

  4. (4)

    Age, sex, social status, and race do not affect the probability of being infected.

A schematic diagram of RD-Covid-19 model is as shown in Fig. 4.

Fig. 4
figure 4

Schematic Diagram of Networked RD-Covid-19 Model

Full size image

The data-driven model estimates the growth curve of the epidemic by fitting the parameters of the model through the available data (confirmed cases of Covid-19) of the public for any country. As mentioned previously, hereafter, estimated values of the parameters (rate of infection and rate of recovery) from the logistic model fed as guess value of the parameters of the SIR model, and subsequently, similar trend follows for the other three networked model, viz., SEIR and SEIQRDP. Parameters of epidemiological models used in our work estimated by the nonlinear least-square fitting of the available data. Levenberg–Marquardt Algorithm [49] and an optimization technique of min-search (basically quadratic programming) used for fitting the model parameters. At the final stage, the SEIQRDP model is executed to compute the time-dependent profile of seven states of the model.

Let us discuss data-driven models that we have investigated, and finally, we have selected a specific model for the present work.

  1. 1.

    Gompertz Model

    $$Q_{t} = cumulative \, confirmed \, cases = a*exp\left( { - b*\exp \left( { - c*\left( {t - t_{0} } \right)} \right)} \right)$$
    (6)

    where, a = predicted maximum of confirmed, b and c are fitting coefficients, t represents the number of days since the first case, and t0 signifies the time when the first case occurred.

  2. 2.

    Logistic Model

    This model predicts the development and transmission trend of the epidemic. Governing equation of this data-driven model is given by

    $$Q_{t} = \frac{a}{1 + exp\left( b - c\left( t - t_{0} \right) \right)},$$
    (7)

    where a = predicted maximum of confirmed cases, where b and c are the fitting coeffcients, t represents the number of days since the first case, t0 signifies the time when the first case occurred.

    The logistic model is used to explore the risk factors of particular disease and predict the probability of a specific disease according to the risk factors.

  3. 3.

    Bertalanffy Model

    This model represents the growth curve model for a time series (cumulative or daily confirmed cases and death cases in case of Covid-19). It is a special case of generalized logistic function. Governing equation of this model is given by

    $$ Q_{t} = a\left( {1 - exp\left( { - b\left( {t - t_{0} } \right)} \right)} \right)^{c}$$
    (8)

    where the symbols have usual significances, like previous other models as mentioned.

  4. (4)

    Monod Kinetic Growth Model

    This model is used to explore the growth of microorganisms. Form of this model is the same as Michaelis–Menten equation and is given by

    $$ Y_{t} = Y_{{max}} \frac{\theta }{{K_{\theta } + \theta }},$$
    (9)

    \( Y_{t}\) specific growth rate of the microorganisms (in this case, coronavirus) \( Y_{{max}} =\) maximum value of the specific growth rate of microorganism, \( \theta\) = concentration (cases) of the limiting substrate for growth, \(K_{\theta }\) = half velocity constant. The present work follows the logistic model Monod Kinetic Growth model (Eq. 9) to explore the coronavirus outbreak of any country and the corresponding growth rate of the event in the same region.

    The second stage of the networked model is SIR, which has already described in Eq. (2). The third stage of the networked model is SEIR model, where an extra compartment explaining the exposed population (E) introduced. The governing one-dimensional differential equation (ODE) of the SEIR epidemiological model is written (Eq. 10) as:

    $${\begin{array}{*{20}c} {\frac{{dS}}{{dt}} = - \frac{{\beta SI}}{N}} \\ {\frac{{dE}}{{dt}} = \frac{{\beta SI}}{N} - \upomega{E}} \\ {\frac{{dI}}{{dt}} = \upomega{E} - \gamma I} \\ {\frac{{dR}}{{dt}} = \gamma I} \\ \end{array}} $$
    (10)

    where, N = S + E + I + R = total population, β = rate of infection, which modeled as = β0 K explaining β0 as the probability of infection per encounter with an infected individual and K as the number of people encountered per day. The parameter ω is modeled as 1/Te, where Te signifies the latent period (days). The average rate of recovery is denoted by the parameter γ = 1/Ti, where Ti is the average recovery time of infectives.

The last stage of networked RD-Covid-19 model is the SEIQRDP model, which is further networked by seven states. Those seven states are: (a) Susceptible (S), (b) Exposed (E), (c) Infected (I), (d) Quarantined (Q), (e) Recovered (R), (f) Dead (D) and (g) Protected (P) or in-susceptible population. This specific model contains six parameters which are defined as:

α—the protection rate,

β—the infection rate,

γ—the inverse of the average latent time,

δ—the rate at which infectious people enter in quarantine,

λ(t)—a time-dependent coefficient used to describe the recovery rate,

κ(t)—a time-dependent coefficient that describes the mortality rate.

The time-dependent coefficients, λ(t) and κ(t) further assumed in the following form:

$$ \lambda (t) = \lambda_{0} (1 - e^{{( - \lambda_{1} t)}} )\,and\,{\mkern 1mu} {\mkern 1mu} \kappa (t) = \kappa_{0} e^{{( - \kappa_{1} t)}} ,where\,{\mkern 1mu} \lambda_{0} ,\lambda_{1} ,\kappa_{0} ,\kappa_{1}\, are\,{\mkern 1mu} constants. $$

The values of λ(t) and κ(t) based on the empirical fitting of some provinces of China data indicate that the gradual increase of recovery rate and fast decrease of mortality rate. The assumptions are reasonably accepted by nature as pandemic always converges to zero while the recovery rate continues to increase towards a saturation level. The other parameters of the SEIQRDP model are constant because they do not fluctuate on time. The dynamic of each state is characterized mathematically by an ordinary differential equation given by (Eq. 11).

$$ \begin{array}{l}\frac{{dS}}{{dt}} = - \alpha S - \frac{{\beta SI}}{N}\\\frac{{dE}}{{dt}} = \frac{{\beta SI}}{N} - \gamma E\\\frac{{dI}}{{dt}} = \gamma E - \delta I\\\frac{{dQ}}{{dt}} = \delta I - \uplambda{Q} - \upkappa{Q}\\\frac{{dR}}{{dt}} = \uplambda{Q}\\\frac{{dD}}{{dt}} = \upkappa{Q}\\\frac{{dP}}{{dt}} = \alpha S\end{array} $$
(11)

where N represents the total population and is written as N = S + E + I + Q + R + D + P.

The networked RD-Covid-19 model estimates the basic reproduction number R0 at its networked stage. Therefore, in the first stage of the network, the output of data-driven (Monod Kinetic growth) and SIR models and the last stage of a network that is an output of SEIQRDP model-based estimated value of R0 are mentioned, which is sufficient to know about the progress of coronavirus outbreak. The time evolution of reproduction number, R is modeled as \(R_{t} = R_{0} \exp \left( - \gamma t \right), \gamma\) signifies here the rate of recovery. There are many methods to estimate R0. In our present work, we have used the next-generation matrix method for determining R0. In the next-generation matrix method, the estimation of R0 is based on the maximum eigenvalue of the product of two matrices F and V−1, which are generated from the system of the differential equation of the specific model in matrix form.

7 Numerical Simulation of RD-Covid-19 Model

The general strategy of simulation of the infectious disease dynamics model for modeling and predicting the number of Covid-19 cases has carried out. The forecasting of RD-Covid-19 model validated with cases in Wuhan, China. Later on, our model implemented to forecast the coronavirus outbreak and epidemic profile of countries like India, Brazil, and Russia. Utilization of the numerical Model is of incredible managing hugeness to survey the effect of segregation of suggestive cases just as the perception of asymptomatic contact cases and to advance proof-based choices and strategy. We accepted no new transmissions from creatures, no distinctions in singular insusceptibility, the time-size of the pandemic is a lot quicker than trademark times for segment forms (normal birth and death), and no differences in common births and passings.

Numerical simulation of any dynamic model (a system of first-order coupled ODE) can be carried out either by the Runge–Kutta method or by explicit finite difference technique. Here we have adopted the fourth order Runge–Kutta method for simulating each networked node (epidemiological model). In the first stage of the RD-Covid-19 networked model we have fitted the Monod Kinetic Growth data-driven model. Subsequently, parameters of the SIR model fitted by Levenberg Marquardt nonlinear least square method based optimization technique. Data used for mounting the model and corresponding simulation captured from John Hopkins University and WHO dashboard [50]. Dataset preprocessed into three groups like (a) cumulative confirmed cases, (b) cumulative recovered cases, and (c) cumulative deaths. Dataset for daily new cases constructed by computing the forward difference of cumulative confirmed cases per day. Similarly, new deaths per day and new recovered cases per day also computed by following a similar strategy. Active cases per day generated by subtracting the cumulative recovered and cumulative deaths from cumulative confirmed cases.

We have divided numerical simulation of RD-Covid-19 into four parts. Part 1 presents the numerical outcome of India; Part 2 of China; Part 3 of Brazil and Part 4 of Russia.. Numerical simulation of each node of RD-Covid-19 model has been carried out with the fitted parameters at each stage, and finally, the simulated outcome of node ‘SEIQRDP’ of RD-Covid-19 shown in Fig. 11. We have developed computer code for numerical simulation of our RD-Covid-19 Model in R software (version 3.6.2) and MATLAB 2017a. The impact of various control measures (e.g., social distance, wearing a mask, and lockdown) implemented in code. In the process, S assumed to be the population of an individual country.

7.1 PART-1: Numerical Outcome of RD-Covid-19 Model Outcome for INDIA

Time histories profile of various events (confirmed cases, death cases, and recovered cases) and epidemic trend of coronavirus outbreak as the outcome of RD-Covid-19 Model for India during the period from January 22, 2020, to July-5, 2020 are shown in Figs. 5, 6, 7, 8, 9, 10 and 11. The results of the epidemic trend (plot) of coronavirus outbreak is as shown in Fig. 10 with a blue line (cases/day). Blue dots represent the actual infection rate (cases/day). A region with different colours separate the transmition phases of the epidemic like the red-colored zone signifies fast growth phase, yellow colored zone presents the transmition to steady state phase and green colored zone presents the ending phase.

Fig. 5
figure 5

Temporal profile of cumulative confirmed cases in India

Full size image
Fig. 6
figure 6

Temporal profile of daily confirmed cases in India

Full size image
Fig. 7
figure 7

Temporal profile of daily death cases in India

Full size image
Fig. 8
figure 8

Temporal profile of daily recovered cases in India

Full size image
Fig. 9
figure 9

Temporal profile of daily active cases in India

Full size image
Fig. 10
figure 10

Epidemic Trend of Coronavirus outbreak in India

Full size image
Fig. 11
figure 11

Numerical simulation of Node SEIQRDP model of RD-Covid-19 (India)

Full size image

7.2 PART-2: Numerical Outcome of RD-Covid-19 Model Outcome for CHINA

Time histories profile of various events (confirmed cases, death cases, and recovered cases) and epidemic trend of coronavirus outbreak as the outcome of RD-Covid-19 Model for China during the period during the period from January 22, 2020, to July-5, 2020 are shown in Figs. 12, 13, 14, 15, 16, 17 and 18. The result of the epidemic trend (plot) of coronavirus outbreak is as shown in Fig. 17 with a blue line (cases/day). Blue dots represent the actual infection rate (cases/day). A region with different colors separate the transition phases of the epidemic like the red-colored zone signifies fast growth phase, yellow-colored zone presents the transition to steady-state phase, and green colored zone presents the ending phase.

Fig. 12
figure 12

Temporal profile of cumulative confirmed cases

Full size image
Fig. 13
figure 13

Temporal profile of daily confirmed cases

Full size image
Fig. 14
figure 14

Temporal profile of daily death cases

Full size image
Fig. 15
figure 15

Temporal profile of daily recovered cases

Full size image
Fig. 16
figure 16

Temporal profile of daily active cases

Full size image
Fig. 17
figure 17

Epidemic Trend of Coronavirus outbreak in China

Full size image
Fig. 18
figure 18

Numerical simulation of Node SEIQRDP model of RD-Covid-19 (China)

Full size image

7.3 PART-3: Numerical Outcome of RD-Covid-19 Model Outcome for BRAZIL

Time histories profile of various events (confirmed cases, death cases, and recovered cases) and epidemic trend of coronavirus outbreak as the outcome of RD-Covid-19 Model for Brazil during the period during the period from January 22, 2020, to July-5, 2020 are shown in Figs. 19, 20, 21, 22, 23 and 24. The result of the epidemic trend (plot) of coronavirus outbreak is as shown in Fig. 23 with a blue line (cases/day). Blue dots represent the actual infection rate (cases/day). A region with different colors separate the transition phases of the epidemic like the red-colored zone signifies fast growth phase, yellow-colored zone presents the transition to steady-state phase, and green colored zone presents the ending phase.

Fig. 19
figure 19

Temporal profile of Cumulative confirmed cases in Brazil

Full size image
Fig. 20
figure 20

Temporal profile of daily confirmed cases in Brazil

Full size image
Fig. 21
figure 21

Temporal profile of daily death cases in Brazil

Full size image
Fig. 22
figure 22

Temporal profile of daily recovered cases in Brazil

Full size image
Fig. 23
figure 23

Epidemic trend of Coronavirus outbreak in Brazil

Full size image
Fig. 24
figure 24

Numerical simulation of Node SEIQRDP model of RD-Covid-19 (Brazil)

Full size image

7.4 PART-4: Numerical Outcome of RD-Covid-19 Model Outcome for RUSSIA

Time histories profile of various events (confirmed cases, death cases, and recovered cases) and epidemic trend of coronavirus outbreak as the outcome of RD-Covid-19 Model for Russia during the period during the period from January 22, 2020, to July-5, 2020 are shown in Figs. 25, 26, 27, 28, 29 and 30. The result of the epidemic trend (plot) of coronavirus outbreak is as shown in Fig. 29 with a blue line (cases/day). Blue dots represent the actual infection rate (cases/day). A region with different colors separate the transition phases of the epidemic like the red-colored zone signifies fast growth phase, yellow-colored zone presents the transition to steady-state phase, and green colored zone presents the ending phase.

Fig. 25
figure 25

Temporal profile of Cumulative confirmed cases in Russia

Full size image
Fig. 26
figure 26

Temporal profile of daily confirmed cases in Russia

Full size image
Fig. 27
figure 27

Temporal profile of daily death cases in Russia

Full size image
Fig. 28
figure 28

Temporal profile of daily recovered cases in Russia

Full size image
Fig. 29
figure 29

Epidemic Trend of Coronavirus outbreak in Russia

Full size image
Fig. 30
figure 30

Numerical simulation of Node SEIQRDP model of RD-Covid-19 (Russia)

Full size image

Values of the fitted parameters of the last node SEIQRDP of RD-Covid-19 Model for various countries (China, India, Brazil, and Russia) tabulated in Table 1. Basic reproduction number (R0), reproduction number (R), and herd immunity threshold concerning the epidemic curve of China, India, Brazil, and Russia tabulated in Table 2. The estimated duration of different stages of epidemic events presented in Table 3. Estimated datum (Dates) of the epidemic stage of China, India, Brazil, and Russia showed in Table 4. Table 5 presents the statistics of total and daily cases.

Table 1 Fitted Value of Parameters of SEIQRDP node of RD-COVD-19 model
Full size table
Table 2 Basic Reproduction number, Reproduction number and Herd Immunity
Full size table
Table 3 Estimated duration of epidemic stage
Full size table
Table 4 Estimated datum of epidemic stage
Full size table
Table 5 Statistics of total and daily cases
Full size table

8 Conclusions

Epidemiological modeling of infectious diseases like Covid-19 has been discussed in detail in this chapter. The chapter discusses various issues associated with the fundamental aspects of the epidemiology of infectious diseases such as contact rate, attack rate, probability of transmission, basic reproduction number, and dynamic growth. Each traditional epidemiological models in this direction are compartmental model, and their evolution are discussed in the chapter. Here, in this chapter, we have presented the design, development and numerical simulation of an innovative networked RD-Covid-19 model. Various traditional models such as SIR, SEIR, and SEIQRDP are networked or cascaded to develop this RD-Covid-19. In our RD-Covid-19 Model, we have demonstrated the technique of fitting of model parameters using a nonlinear least square optimization method wherein we have used the Levenberg–Marquardt algorithm. Initially, guess the value of the model parameters required for fitting (mainly, infection rate and recovery rate) are guessed and subsequently iterated and improved by a data driven logistic growth model (Monod Kinetic Growth Model). Subsequently, guess values are used as input to the various stages of the network so that parameters have improved at every stage. Hence, the final stage of the system of RD-Covid-19 Model (SEIQRDP) generated the optimal values of the fitted parameter. The profile of various states (infected, quarantined, recovered, etc.) of the model have been created by using the optimal values of the parameters. The severity of the model is presented by estimating the basic reproduction number, R0. The epidemic trend of four countries, viz. India, China, Brazil, and Russia is generated as an outcome of RD-Covid-19 model. Results are in agreement with the result reported in the WHO dashboard. Future perspectives of this kind of study related to dynamic epidemiology will extend to compute risk management, including the cognitive behavior of humans facing this infectious disease under various control measures such as lockdown mainly and also social distance maintenance.