Abstract
Linguistic Pythagorean fuzzy sets (LPFSs), which use linguistic terms to represent membership degree and non-membership degree, have been proved to be effective to deal with uncertainties and vagueness in information and data. However, LPFSs still have drawbacks in depicting fuzzy decision-making information, i.e., they fail to handle multi-attribute group decision-making (MAGDM) situations wherein decision experts are hesitant among some series of linguistic terms when determining the linguistic membership and non-membership degrees. To efficiently and accurately express fuzzy attribute values provided by decision experts, this paper extends LPFSs to dual hesitant linguistic Pythagorean fuzzy sets (DHLPFSs), which allow the possible membership and non-membership degrees to be denoted by a collection of linguistic terms. We further study operational rules, ranking method, and aggregation operators of DHLPFSs, and based on these achievements, we introduce a new MAGDM method. To more comprehensively capture group’s evaluation information, we then generalize DHLPFSs to probabilistic DHLPFSs (PDHLPFSs), by taking probabilistic information of each linguistic term into count. For the sake of usage of PDHLPFSs in MAGDM problems, we continue to investigate their operations, comparison method, and aggregation operators and introduce a novel decision-making method. Finally, illustrative examples are provided to show the effectiveness of the new MAGDM methods.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Linguistic Pythagorean fuzzy sets
- Dual hesitant linguistic Pythagorean fuzzy sets
- Probabilistic dual hesitant linguistic Pythagorean fuzzy sets
- Aggregation operator
- Multi-attribute group decision-making
1 Introduction
In modern decision-making sciences, multi-attribute group decision-making (MAGDM) refers to a series of decision issues where domain decision experts (DEs) are required to provide their evaluations over feasible alternatives under multiple attributes [1,2,3,4,5]. Some techniques or methods are then applied to help DEs to obtain the ranking order of candidate alternatives so that the optimal one(s) is obtained accordingly. However, it is quite difficult to deal with the inherent fuzziness and uncertainties in practical MAGDM problems. Numerous scholars and scientists devoted themselves to discover tools that can effectively handle fuzzy information in data. Intuitionistic fuzzy sets (IFSs) [6], originally generated by Atanassov have the capability of representing uncertain information and they depict fuzzy phenomenon from both positive and negative perspectives. In other words, by simultaneously incorporating membership degree (MD) and non-membership degree (NMD), IFSs can more comprehensively and accurately describe fuzzy and vague decision-making information. Due to this characteristic, IFSs-based MAGDM theory and methods have been active fields, and quite a few new achievements have been made in the past couple of years. For example, in [7] Xu originated the theory of aggregation operators (AOs) for intuitionistic fuzzy numbers (IFNs). After it, some other AOs for IFNs, such as intuitionistic fuzzy Bonferroni mean [8], intuitionistic fuzzy point operators [9], intuitionistic fuzzy Maclaurin symmetric mean [10], intuitionistic fuzzy Muirhead mean [11], intuitionistic fuzzy power average operators [12], intuitionistic fuzzy power Bonferroni mean [13], etc., have been proposed one after another.
MDs and NMDs of IFSs are denoted by crisp numbers, however, which is sometimes difficult to be determined by DEs. As MAGDM problems in practice are becoming more and more complicated, rather than crisp numbers, DEs would like to employ linguistic terms to denote MDs and NMDs to express their assessments. Motivated by this fact, Chen et al. [14] generalized IFSs and proposed linguistic intuitionistic fuzzy sets (LIFSs), which use linguistic terms to denote MD and NMD. Linguistic terms are quite similar to natural language and so that it is more convenient for DEs to use LIFSs to provide their evaluation values. After the appearance of LIFS, Ou et al. [15] introduced the LIFS-TOPSIS method to deal with MAGDM problems. Yuan et al. [16] proposed a series of linguistic intuitionistic fuzzy (LIF) Shapely AOs to handle decision-making issues with LIF numbers (LIFNs). Meng et al. [17] studied preference relations under LIFSs and applied them in decision-making problems. Liu and You [18] proposed a collection of novel LIF Heronian mean AOs under Einstein t-norm and t-conorm. Liu and Qin [19] put forward LIF power average operator in order to reduce the negative influence of unduly high or low aggregated LIFNs on the final results. Liu and Qin [20], and Liu and Liu [21] further presented LIF Maclaurin symmetric mean operators and LIF Hamy mean operators to capture the interrelationship among multiple aggregated LIFNs. To effectively handle heterogeneous interrelationship among LIFNs, Liu and his colleagues [22] defined LIF partitioned Heronian mean operators. Garg and Kumar [23] further introduced novel LIF power average operators and the corresponding decision-making method based on set pair analysis. Zhang et al. [24] proposed the LIF-ELECTRE decision-making method and applied in coal mine safety evaluation problems. Peng and Wang [25] introduced a LIF MAGDM method based on cloud model and studied its application in selecting sustainable energy crop. For more studies on LIFSs-based MAGDM methods, readers are suggested to refer [26,27,28,29,30].
Aforementioned literatures reveal that LIFSs are capable to depict fuzzy evaluation values provided by DEs effectively, however, they still have drawbacks when dealing with some practical decision-making situations. The definition of LIFS is as follows: let \(\tilde{S} = \left\{ {s_{\alpha } \left| {s_{0} \le s_{\alpha } \le s_{t} ,\alpha \in \left[ {0,t} \right]} \right.} \right\}\) be a predefined continuous linguistic term set, then a LIFS defined on \(\tilde{S}\) can be expressed as \(A = \left\{ {\left( {x,s_{\theta } \left( x \right),s_{\sigma } \left( x \right)} \right)\left| {x \in X} \right.} \right\}\). As is known, A should satisfy the constraint that \(\theta +\upsigma \le t\), which cannot be always strictly satisfied in some practical MAGDM problems. For example, an ordered pair \(\left( {s_{3} ,s_{4} } \right)\) is used to depict a DE’s evaluation value, where \(s_{l}\) is a linguistic term and \(l \in \left[ {0,6} \right]\). As \(3 + 4 \le 6\), the evaluation value \(\left( {s_{3} ,s_{4} } \right)\) cannot be handled by LIFSs, which illustrates the weakness of LIFSs. In order to more accurately capture DEs’ complicated and uncertain decision information and handle more difficult decision situations, Garg [31] proposed a new tool, called linguistic Pythagorean fuzzy sets (LPFSs), which are motivated by Pythagorean fuzzy sets (PFSs) that introduced by Yager [32]. As is widely known, the constraint of PFSs is that the square sum of MD and NMD is not greater than one and this characteristic makes PFSs more powerful and flexible than IFSs, gaining great interests from scholars [33,34,35,36,37,38,39,40,41,42]. In LPFSs, MDs and NMDs are denoted by linguistic terms, satisfying the constraint that \(\theta^{2} + \sigma^{2} \le t^{2}\) (\(s_{\theta }\) and \(s_{\sigma }\) denote the MD and NMD, respectively, and \(s_{t}\) is the largest linguistic term of the predefined linguistic term set), and due to this reason, LPFSs can describe lager information span than LIFSs. In [31], Garg proposed basic operational linguistic Pythagorean fuzzy (LPF) values, presented their fundamental AOs, and applied in MAGDM problems. After it, Liu et al. [43] studied LPF operational rules, AOs, and MAGDM method based on Archimedean t-norm and t-conorm. Han et al. [44] introduced distance and entropy measures of LPFSs and based on which, an LPF-TOPSIS decision-making method was originated. To felicitously handle MAGDM issues where interrelationship among attributes is heterogeneous, Lin et al. [45] put forward the LPF partitioned Bonferroni mean operators.
There exists high indeterminacy and hesitancy when providing MDs and NMDs of evaluation values in the most practical MAGDM processes. Hence, the key problem is to effectively deal with the inherent fuzziness and uncertainties of data and DEs’ hesitancy. For instance, Torra [46] proposed the concept of hesitant fuzzy sets (HFSs) by considering multiple possible MDs in an evaluation element. Compared with the classical fuzzy set theory [47], HFSs can better depict DEs’ hesitancy. Similarly, Zhu et al. [48] introduced the dual HFSs (DHFSs) by taking not only multiple MDs but also NMDs into account. DHFSs are regarded as an extension of IFS, as they emphasize multiple values of degrees instead single ones. Another example is dual hesitant Pythagorean fuzzy sets introduced by Wei et al. [49], which consider more than one Pythagorean fuzzy MDs and NMDs in the traditional PFSs. These publications remind scholars and DEs an extensively existing phenomenon that most decisions are made in a hesitant fuzzy environment and DEs’ hesitancy should be taken into consideration before determining the rank of feasible alternatives. In LPF, decision-making environment, we always encounter MAGDM situations wherein DEs are hesitant among a set of linguistic terms when giving the MDs and NMDs an evaluation value. Motivated by DHFSs which allow the existence of multiple MDs and NMDs in a decision evaluation value, this paper extends the traditional LPFSs to a hesitant fuzzy environment and propose dual hesitant linguistic Pythagorean fuzzy sets (DHLPFSs), which permit MDs and NMDs to be denoted by a set of linguistic terms. Compared with LPFSs, DHLPFSs are more flexible and can depict attribute values more accurately. In this chapter. We first give the definition, operational rules, comparison method, and AOs of DHLPFSs and propose a novel MAGDM method with DHLPFSs. We also show the performance of the proposed new method through illustrative examples.
Additionally, to more accurately capture DEs’ evaluation value in hesitant fuzzy decision-making environment, not only each member in an evaluation element but also its probabilistic information should be considered. For example, Zhang et al. [50] capture the probability of each member in HFSs and proposed the probabilistic HFSs (PHFSs). Compared with HFSs, the PHFSs not only depict the hesitant fuzzy MDs but also the corresponding probabilistic information. Afterward, PHFSs have been successfully applied in various fields, such as public company efficiency evaluation [51], hospital evaluation [52], virtual reality project declaration evaluation [53], selection of the most influential teacher [54], etc. Similarly, Hao et al. [55] extended DHFSs to probabilistic DHFSs by taking the probabilities of possible MDs and NMDs into account. The ability of efficiency of probabilistic DHFSs to depict DEs’ evaluation values is further studied in [56,57,58]. Additionally, some other new information representation tools were also proposed, such as probabilistic linguistic terms set [59], probabilistic linguistic dual hesitant fuzzy sets [60], and probabilistic single-valued neutrosophic hesitant fuzzy sets [61]. These publications motivate us to further extend DHLPFSs to a more generalized form, i.e., probabilistic DHLPFSs (PDHLPFSs). The advantages of PDHLPFSs are outstanding. First, they allow the MD and NMD to be denoted by two collections of possible linguistic terms, which can comprehensively describe DEs’ high hesitancy. Second, they also consider the corresponding probabilistic information of each linguistic term, which can more effectively depict group’s evaluation values. For the sake of applications of PDHLPFSs in MAGDM, the basic operational laws, comparison method, and AOs of PDHLPFSs are studied. Finally, the main steps of solving a MAGDM problem under PDHLPFSs are presented.
The main motivations of our works are to propose novel MAGDM methods, that only not more accurately depict DEs’ evaluation information but also help them to appropriately determine the optimal alternatives. The main contributions of this chapter are four-fold. First, two information expression tools were proposed, namely DHLPFSs and PDHLPFSs. These two fuzzy set theories have obvious advantages and superiorities in depicting DEs’ evaluations. Second, we proposed a series of AOs to fuse DHLPFSs and PDHLPFSs, which are potential for introducing novel decision-making methods. Third, we proposed two new MAGDM methods. Finally, real MAGDM problems were employed to prove the validity of our methods. The rest of this chapter is organized as follows. Section 2 recalls basic notions which will be used in the following sections. Section 3 introduces DHLPFSs and the corresponding MAGDM method. Section 4 further proposes DHLPFSs and studies their applications in MAGDM. Conclusion remarks can be found in Sect. 5.
2 Basic Concepts
This section briefly reviews basic notions that will be used in the following sections.
Definition 1
([31]) Let X be a fixed set and \(\tilde{S} = \left\{ {s_{0} ,s_{1} ,s_{2} \ldots ,s_{l} } \right\}\) be a continuous linguistic term set with odd cardinality. A linguistic Pythagorean fuzzy set (LPFS) defined in X is given as
where \(s_{\alpha } \left( x \right),s_{\beta } \left( x \right) \in S_{{\left[ {0,l} \right]}}\), \(s_{\alpha }\), and \(s_{\beta }\) represent the linguistic MD and linguistic NMD, respectively, such that \(0 \le \alpha^{2} + \beta^{2} \le l^{2}\). For convenience, the ordered pair \(\gamma = \left( {s_{\alpha } ,s_{\beta } } \right)\) is called a linguistic Pythagorean fuzzy value (LPFV). The linguistic indeterminacy degree of \(\gamma\) is expressed as \(\uppi \left( x \right) = s_{{\left( {l^{2} - \alpha^{2} - \beta^{2} } \right)^{1/2} }}\).
The basic operational rules of LPFVs are presented as follows.
Definition 2
([31]) Let \(\gamma_{1} = \left( {s_{{\alpha_{1} }} ,s_{{\beta_{1} }} } \right)\), \(\gamma_{2} = \left( {s_{{\alpha_{2} }} ,s_{{\beta_{2} }} } \right)\), and \(\gamma = \left( {s_{\alpha } ,s_{\beta } } \right)\) be LPFVs and \(\lambda\) be a positive real number, then
-
(1)
\(\gamma_{1} \oplus \gamma_{2} = \left( {{\varvec{s}}_{{\left( {\alpha_{1}^{2} + \alpha_{2}^{2} - \alpha_{1}^{2} \alpha_{2}^{2} /l^{2} } \right)^{1/2} }} ,{\varvec{s}}_{{\left( {\beta_{1} \beta_{2} /l} \right)}} } \right)\);
-
(2)
\(\gamma_{1} \otimes \gamma_{2} = \left( {{\varvec{s}}_{{\left( {\alpha_{1} \alpha_{2} /l} \right)}} ,{\varvec{s}}_{{\left( {\beta_{1}^{2} + \beta_{2}^{2} - \beta_{1}^{2} \beta_{2}^{2} /l^{2} } \right)^{1/2} }} } \right)\);
-
(3)
\(\lambda \gamma = \left( {{\varvec{s}}_{{l\left( {1 - \left( {1 - \alpha^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} ,{\varvec{s}}_{{l\left( {\beta /l} \right)^{\lambda } }} } \right)\);
-
(4)
\(\gamma^{\lambda } = \left( {{\varvec{s}}_{{l\left( {\alpha /l} \right)^{\lambda } }} ,{\varvec{s}}_{{l\left( {1 - \left( {1 - \beta^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} } \right)\).
Garg [31] proposed a method to compare any two LPFVs.
Definition 3
([31]) Let \(\gamma = \left( {s_{\alpha } ,s_{\beta } } \right) \in\Gamma _{{\left[ {0,l} \right]}}\) be a LPFV, then the score function \(S\left( \gamma \right)\) of \(\gamma\) is expressed as
and the accuracy function \(H\left( \gamma \right)\) is defined as
where \(S\left( \gamma \right),H\left( \gamma \right) \in S\). Let \(\gamma_{1} = \left( {s_{{\alpha_{1} }} ,s_{{\beta_{1} }} } \right)\) and \(\gamma_{2} = \left( {s_{{\alpha_{2} }} ,s_{{\beta_{2} }} } \right)\) be any two LPFVs, then
-
(1)
If \(S\left( {\gamma_{1} } \right) > S\left( {\gamma_{2} } \right)\), then \(\gamma_{1} > \gamma_{2}\);
-
(2)
If \(S\left( {\gamma_{1} } \right) = S\left( {\gamma_{2} } \right)\), then
-
If \(H\left( {\gamma_{1} } \right) > H\left( {\gamma_{2} } \right)\), then \(\gamma_{1} > \gamma_{2}\);
-
If \(H\left( {\gamma_{1} } \right) = H\left( {\gamma_{2} } \right)\), then \(\gamma_{1} = \gamma_{2}\).
-
3 Dual Hesitant Linguistic Pythagorean Fuzzy Sets and Their Applications in MAGDM
In this section, we introduce the notion of DHLPFSs and study their application in MAGDM problems. For this purpose, we first introduce the motivations to explain why we propose DHLPFSs and why we need them. Afterward, some related notions, such as operational rules, comparison method, and AOs are proposed. Finally, we employ DHLPFSs as well as their AOs to solve MAGDM problems.
3.1 Motivations and Necessity of Proposing DHLPFSs
In LPFSs, MD and NMD are denoted by two linguistic terms. As is known, linguistic terms set and linguistic terms are similar to natural language so that LPFSs provide DEs a convenient and natural manner to express their evaluation values. Due to this reason, LPFSs are more suitable than PFSs to depict DEs’ fuzzy and complex evaluation information. However, the traditional LPFSs still have limitations in some practical MAGDM problems. As real decision-making problems are very complicated, sometimes it is difficult for DEs to provide single linguistic terms for MD and NMD. Actually, DEs are always hesitant among a collection of possible linguistic terms when determining MDs and NMDs of their evaluation values. To better demonstrate this phenomenon, we provide the following example.
Example 1
Suppose there are three professors and they are invited to evaluate the innovativeness of a doctoral student’s research proposal. To more accurately and effectively evaluate the quality and innovation, DEs are permitted to use multiple values to denote MDs and NMDs of their evaluation values. Let S be a given linguistic term set, where S = {s0 = very poor, s1 = poor, s2 = slightly poor, s3 = fair, s4 = slightly good, s5 = good, s6 = slightly good}. the three professors use multiple linguistic terms to express their evaluation information and DEs’ evaluation opinions are listed in Table 1.
Take the first professor as an example, as seen in Table 1, he/she is hesitant between s4 and s5 when giving MD and s1, s2 and s3 when providing MD. It is obvious that in the framework of LPFSs, the overall evaluation values of the decision group cannot be denoted. This is because LPFS theory only allows single MD and NMD, and so that it is insufficient to handle Example 1. In practical MAGDM problems, due to many reasons, such as lacking prior knowledge or time, DEs often hesitate among several values when providing MDs and NMDs and obviously LPFSs are incapable to handle these situations. Therefore, it is necessary to study LPFSs under hesitant fuzzy decision environment.
3.2 Definition of DHLPFSs
Definition 4
Let X be a fixed set and \(\tilde{S} = \left\{ {s_{\alpha } \left| {0 \le \alpha \le l} \right.} \right\}\) be continuous linguistic term set with odd cardinality. A dual hesitant linguistic Pythagorean fuzzy set (DHLPFSs) defined on X is expressed as
where \(h_{A} \left( x \right),g_{A} \left( x \right) \subseteq \tilde{S}\) are two sets of some linguistic terms, denoting the possible linguistic MDs and linguistic NMDs of element \(x \in X\) to the set D, respectively, such that \(\sigma^{2} + \eta^{2} \le l^{2}\), where \(s_{\sigma } \in h_{D} \left( x \right)\), and \(s_{\eta } \in g_{D} \left( x \right)\) for \(x \in X\). For convenience, we call the ordered pair \(d\left( x \right) = \left( {h_{D} \left( x \right), g_{D} \left( x \right)} \right)\) a dual hesitant linguistic Pythagorean fuzzy element (DHLPFE), which can be denoted as \(d = \left( {h, g} \right)\), where \(s_{\sigma } \in h\), \(s_{\eta } \in g\) and \(\sigma^{2} + \eta^{2} \le l^{2}\).
Definition 4 reveals that DHLPFSs can be regarded as a generalized form of LPFSs, by considering situations of the existence of multiple MDs and NMDs. In other words, LPFS is a special case of DHLPFSs. Hence, the proposed DHLPFSs are more suitable to deal with decision-making cases wherein DEs have different opinions and they cannot reach an agreement. In Example 1, if we use DHLPFSs to denote the overall evaluation value, then it should be d = {{s1, s2, s3, s4, s5}, {s0, s1, s2, s3}}, which is obviously a DHLPFE.
3.3 Operations of DHLPFEs
Based on the definition of DHLPFEs and the operations principle of DHFEs, we propose some basic operational rules of DHLPFEs.
Definition 5
Let \(d_{1} = \left( {h_{1} ,g_{1} } \right)\), \(d_{2} = \left( {h_{1} ,g_{2} } \right)\), and \(d = \left( {h,g} \right)\) be any three DHLPFEs and \(\lambda\) be a positive real number, then
-
(1)
\(d_{1} \oplus d_{2} = \bigcup\nolimits_{{\sigma_{1} \in h_{1} ,\sigma_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} {\left\{ {\left\{ {s_{{\left( {\sigma_{1}^{2} + \sigma_{2}^{2} - \sigma_{1}^{2} \sigma_{2}^{2} /l^{2} } \right)^{1/2} }} } \right\},\left\{ {s_{{\left( {\eta_{1} \eta_{2} /l} \right)}} } \right\}} \right\}}\);
-
(2)
\(d_{1} \otimes d_{2} = \bigcup\nolimits_{{\sigma_{1} \in h_{1} ,\sigma_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} {\left\{ {\left\{ {s_{{\left( {\sigma_{1} \sigma_{2} /l} \right)}} } \right\},\left\{ {s_{{\left( {\eta_{1}^{2} + \eta_{2}^{2} - \eta_{1}^{2} \eta_{2}^{2} /l^{2} } \right)^{1/2} }} } \right\}} \right\}}\);
-
(3)
\(\lambda d = \bigcup\nolimits_{\sigma \in h,\eta \in g} {\left\{ {\left\{ {s_{{l\left( {1 - \left( {1 - \sigma^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} } \right\},\left\{ {s_{{l\left( {\eta /l} \right)^{\lambda } }} } \right\}} \right\}}\);
-
(4)
\(d^{\lambda } = \bigcup\nolimits_{\sigma \in h,\eta \in g} {\left\{ {\left\{ {s_{{l\left( {\sigma /l} \right)^{\lambda } }} } \right\},\left\{ {s_{{l\left( {1 - \left( {1 - \eta^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} } \right\}} \right\}}\).
Example 2
Let \(d_{1} = \left\{ {\left\{ {s_{3} ,s_{4} ,s_{5} } \right\},\left\{ {s_{2} ,s_{3} } \right\}} \right\}\) and \(d_{2} = \left\{ {\left\{ {s_{2} ,s_{4} } \right\},\left\{ {s_{4} } \right\}} \right\}\) be two DHLPFEs derived from a pre-defined linguistic term set \(\tilde{S} = \left\{ {s_{\alpha } \left| {0 \le \alpha \le 6} \right.} \right\}\), then
\(d_{1} \oplus d_{2} = \left\{ {\left\{ {s_{3.4641} ,s_{4.5826} ,s_{4.2687} ,s_{4.9889} ,s_{5.1208} ,s_{5.4671} } \right\},\left\{ {s_{1.3333} ,s_{2.0000} } \right\}} \right\}\);
\(d_{1} \otimes d_{2} = \left\{ {\left\{ {s_{1.0000} ,s_{1.333} ,s_{2.6667} ,s_{3.3333} } \right\},\left\{ {s_{4.2687} ,,s_{4.5826} } \right\}} \right\}\);
\(3d_{1} = \left\{ {\left\{ {s_{4.5621} ,,s_{5.4614} ,s_{5.9138} } \right\},\left\{ {s_{0.2222} ,s_{0.7500} } \right\}} \right\}\);
\(d_{1}^{3} = \left\{ {\left\{ {s_{0.7500} ,s_{1.7778} ,s_{3.4722} } \right\},\left\{ {s_{3.2735} ,s_{4.5621} } \right\}} \right\}\).
Theorem 1
Let \(d_{1} = \left( {h_{1} ,g_{1} } \right)\), \(d_{2} = \left( {h_{1} ,g_{2} } \right)\), and \(d = \left( {h,g} \right)\) be any three DHLPFEs, then
-
(1)
\(d_{1} \oplus d_{2} = d_{2} \oplus d_{2}\);
-
(2)
\(d_{1} \otimes d_{2} = d_{2} \otimes d_{1}\);
-
(3)
\(\lambda \left( {d_{1} \oplus d_{2} } \right) = \lambda d_{1} \oplus \lambda d_{2}\);
-
(4)
\(\lambda_{1} d \oplus \lambda_{2} d = \left( {\lambda_{1} + \lambda_{2} } \right)d,\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right)\);
-
(5)
\(d^{{\lambda_{1} }} \otimes d^{{\lambda_{2} }} = d^{{\lambda_{1} + \lambda_{2} }} ,\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right)\);
-
(6)
\(d_{1}^{\lambda } \otimes d_{2}^{\lambda } = \left( {d_{1} \otimes d_{2} } \right)^{\lambda } ,\left( {\lambda \ge 0} \right)\).
Proof It is easy to prove that (1) and (2) hold, in the following we attempt to prove other formulas. According to Definition 5, we have
and
which proves the correctness of (3).
Meanwhile, we can obtain that
and
which proves the validity of (4).
Moreover,
which proves the rightness of (5).
Besides,
In addition,
which demonstrates (6) holds.
3.4 Comparison Method of DHLPFEs
To rank DHLPFEs, we provide the following comparison method.
Definition 6
Let \(d = \left( {h,g} \right)\) be a DHLPFEs, the score function \(\tau \left( d \right)\) of d is expressed as
and the accuracy function \(\varphi \left( d \right)\) is defined as
where #h and #g denote the numbers of elements in h and g. For any two DHLPFEs d1 and d2,
-
(3)
If \(\tau \left( {d_{1} } \right) > \tau \left( {d_{2} } \right)\), then \(d_{1} > d_{2}\);
-
(4)
If \({ }\tau \left( {d_{1} } \right) = \tau \left( {d_{2} } \right)\), then
-
If \(\varphi \left( {d_{1} } \right) > \varphi \left( {d_{2} } \right)\), then \(d_{1} > d_{2}\);
-
If \(\varphi \left( {d_{1} } \right) = \varphi \left( {d_{2} } \right)\), then \(d_{1} = d_{2}\).
-
Example 3
Let \(\tilde{S} = \left\{ {s_{\alpha } |0 \le \alpha \le 6} \right\}\) be a pre-defined continuous linguistic term set, and \(d_{1} = \left\{ {\left\{ {s_{0} ,s_{2} ,s_{3} } \right\},\left\{ {s_{4} ,s_{5} } \right\}} \right\}\) and \(d_{2} = \left\{ {\left\{ {s_{1} ,s_{3} } \right\},\left\{ {s_{2} ,s_{3} ,s_{5} } \right\}} \right\}\) be two DHLPFEs defined on \(\tilde{S}\), then we have
According to Definition 6, we can get \(d_{2} > d_{1}\).
3.5 Some Basic Aggregation Operators of DHLPFEs
To aggregate attribute values under DHLPFSs, we propose a series of weighted AOs for DHLPFEs and discuss their properties.
Definition 7
Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of DHLPFEs, and let \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\) be the weight vector, such that \(0 \le w_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). The dual hesitant linguistic Pythagorean fuzzy weighted average (DHLPFWA) operator is defined as
Based on the operations of DHLPFEs, the following aggregated value can be obtained.
Theorem 2
Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be collection of DHLPFEs, then the aggregation result by using the DHLPFWA operator is also a DHLPFE and
Proof When n = 2, then
and
Then
which implies that Eq. (8) holds for n = 2.
In addition, we assume Eq. (8) holds for n = k, i.e.,
then when n = k + 1, we can obtain
i.e., Eq. (8) holds for n = k + 1. Therefore, (12) holds for all n. The proof of Theorem 2 is completed.
In the following, we investigate some properties of DHLPFWA operator.
Theorem 3
(Monotonicity) Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\) and \(d_{i}^{*} = \left( {h_{i}^{*} ,g_{i}^{*} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be two collections of DHLPFEs, where \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) and \(s_{{\sigma_{i}^{*} }} \in h_{i}^{*}\), \(s_{{\eta_{i}^{*} }} \in g_{i}^{*} .\) For \(\forall i = 1,2, \ldots ,n\), if \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\), then
Proof For any \(i\), there are \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\). For the terms in the aggregated results, we have
According to Definition 6, we can get \(DHLPFWA\left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \le DHLPFWA\left( {d_{1}^{*} ,d_{2}^{*} , \ldots ,d_{n}^{*} } \right) \) with equality if and only if \(s_{{\sigma_{i} }} = s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} = s_{{\eta_{i}^{*} }}\) for all \(i\).
Theorem 4
(Boundedness) Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of DHLPFEs. For each \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) \(\left( {i = 1,2, \ldots ,n} \right)\), let \(d^{ - } = \left( {s_{{{\text{min}}\{ \sigma_{i} \} }} ,s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right)\), \(d^{ + } = \left( {s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}} ,s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right)\). Then
Proof For \(\forall i = 1,2, \ldots ,n\), we have \(s_{{{\text{min}}\{ \sigma_{i} \} }} \le s_{{\sigma_{i} }} \le s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}}\), \(s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} \le s_{{\eta_{i} }} \le s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}}\). Then
Further,
According to Definition 6, we have \(DHLPFWA\left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \ge DHLPFWA\left( {d^{ - } ,d^{ - } , \ldots ,d^{ - } } \right)\) with equality if and only if \(d_{i}\) is same as \(d^{ - }\). Similarly, \(DHLPFWA\left( {d_{1} ,d_{2} , \ldots ,d_{n} } \right) \le DHLPFWA\left( {d^{ + } ,d^{ + } , \ldots ,d^{ + } } \right)\) with equality if and only if \(d_{i}\) is same as \(d^{ + }\) can be obtained. So, the proof of the theorem is completed.
Definition 8
Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of DHLPFEs, and let \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\) be the weight vector, such that \(0 \le w_{i} \le 1\) and \(\mathop \sum \limits_{i = 1}^{n} w_{i} = 1\). The dual hesitant linguistic Pythagorean fuzzy weighted geometric (DHLPFWG) operator is defined as
Theorem 5
Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be collection of DHLPFEs, then the aggregation result by using the DHLPFWG operator is also a DHLPFE and
The proof of Theorem 5 is similar to that of Theorem 2, which is omitted here. In addition, DHLPFWG operator has the following properties and the proofs are similar to those of Theorems 3 and 4.
Theorem 6
(Monotonicity) Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\) and \(d_{i}^{*} = \left( {h_{i}^{*} ,g_{i}^{*} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be two collections of DHLPFEs, where \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) and \(s_{{\sigma_{i}^{*} }} \in h_{i}^{*}\), \(s_{{\eta_{i}^{*} }} \in g_{i}^{*} .\) For \(\forall i = 1,2, \ldots ,n\), if \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\), then
Theorem 7
(Boundedness) Let \(d_{i} = \left( {h_{i} ,g_{i} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of DHLPFEs. For each \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) \(\left( {i = 1,2, \ldots ,n} \right)\), let \(d^{ - } = \left( {s_{{{\text{min}}\{ \sigma_{i} \} }} ,s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right)\), \(d^{ + } = \left( {s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}} |,s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right)\). Then
3.6 A MAGDM Method Based on DHLPFSs
In this section, we study DHLPFSs and their AOs in MAGDM problems and propose a new MAGDM method. We further provide a real decision-making example to illustrate the effectiveness of the new method.
3.6.1 Description of a Typical MAGDM Problem Under DHLPFSs
A typical MAGDM problem under DHLPFSs can be described as follows: Let \(A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{m} } \right\}\) be a set of candidates and \(G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{n} } \right\}\) be set of attributes. The weight vector of attributes is \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\), such that \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\) and \(0 \le w_{j} \le 1\). A group of DEs \(D = \left\{ {D_{1} ,D_{2} , \ldots ,D_{t} } \right\}\) is invited to assess the performance of all the alternatives. The weight vector of DEs is \(\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{t} } \right)^{T}\), such that \(0 \le \lambda_{e} \le 1\) and \(\sum\nolimits_{e = 1}^{t} {\lambda_{e} } = 1\). Let \(\tilde{S} = \left\{ {s_{h} \left| {h \in \left[ {0,l} \right]} \right.} \right\}\) be a pre-defined continuous linguistic term set. To properly evaluate the feasible alternatives, for attribute \(G_{j} \left( {j = 1,2, \ldots ,n} \right)\) of \(A_{i} \left( {i = 1,2, \ldots ,m} \right)\), DE \(D_{e} \left( {e = 1,2, \ldots ,t} \right)\) uses a DHLPFEs \(d_{ij}^{e} = \left( {h_{ij}^{e} ,g_{ij}^{e} } \right)\) defined on \(\tilde{S}\) to express his/her evaluation information. Finally, a series of dual hesitant linguistic Pythagorean fuzzy decision matrices are obtained. In the following, based on the proposed AOs we further present a method to solve this problem.
3.6.2 The Steps of a Novel MAGDM Method Based on DHLPFEs
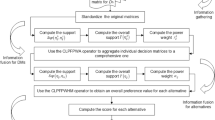
Step 1. Normalize the original decision matrix. In most practical MAGDM problems, there are two types of attributes, i.e., benefit type and cost type. Hence, the original decision matrices should be normalized according to the following formula:
Step 2. Compute the overall decision matrix. For alternative \(X_{i} \left( {i = 1,2, \ldots ,m} \right)\), use DHLPFWA operator
or the DHLPWG operator
to determine the comprehensive evaluation matrix.
Step 3. Compute the final overall evaluation values of alternatives. For alternative \(X_{i} \left( {i = 1,2, \ldots ,m} \right)\), use DHLPFWA operator
or the DHLPWG operator
to compute its comprehensive evaluation value.
Step 4. Calculate the score value \(S\left( {d_{i} } \right)\) and accuracy value \(H\left( {d_{i} } \right)\) of \(d_{i}\).
Step 5. Rank all the alternatives according to the score and accuracy values.
3.6.3 An Illustrative Example
Example 5
In order to improve the accommodation conditions of students, a university plans to install air conditioners in student dormitories. After primary evaluation, there are four suppliers to be select (A1, A2, A3, and A4). In order to choose the optimal air conditioners supplier, the university arranges an expert group composed of students and teachers to evaluate all candidate alternatives. All the five possible candidates are evaluated under four attributes, namely reputation (G1), competitive power (G2), quality of products (G3), and price advantage (G4). The weight vector of attributes is \(w = \left( {0.3,0.1,0.2,0.4} \right)^{T}\). We assume there are three DEs (D1, D2, and D3) whose weight is \(\delta = \left( {0.243,0.514,0.243} \right)^{T}\). Let S = {s0 = extremely poor, s1 = very poor, s2 = poor, s3 = slightly poor, s4 = fair, s5 = slightly good, s6 = good, s7 = very good, s8 = extremely good} be a linguistic term set, and DEs use DHLPFEs to express their evaluation values. The original decision matrices are listed in Tables 2, 3, 4. In the following, we use the proposed MAGDM method to determine the most suitable air conditioners supplier.
Step 1. It is easy to find out that all attributes are benefit types and hence the original decision matrices do not need to be normalized.
Step 2. Use the DHLPFWA operator to compute the comprehensive decision matrix, which is shown in Table 5.
Step 3. Use the DHLPFWA to compute the comprehensive evaluation values of alternatives. As the final overall evaluation values of all the feasible alternatives are too complicated, we omit them here.
Step 4. Compute score values of alternatives according to Definition 6 and we can get the following results:
Step 5. Based on the score values presented in the afore step, we get the ranking order of alternatives, i.e., \(A_{3} \succ A_{1} \succ A_{2} \succ A_{4}\), and A3 is the the best alternative.
In step 2, if the DHLPFWG operator is used to compute the comprehensive decision matrix, then we can get the following results (see Table 6).
Then, we continue to use the DHLPFWG operator to compute the overall values and calculate the score values according to Definition 6, we have
Therefore, the ranking order of alternatives is \(A_{2} \succ A_{3} \succ A_{1} \succ A_{4}\), and A2 is best alternative.
3.6.4 Further Discussion
This section proposes a new MAGDM method wherein DHLPFSs are used to property DEs’ evaluation values. The main advantages of our developed decision-making method are two-fold. First, it allows attribute values or DEs’ evaluation values to be denoted by linguistic terms, which provides DEs a flexible and reliable manner to express their assessments. In actual decision-making situations, DEs usually would like to use linguistic terms numbers to evaluate the performance of possible alternatives. Hence, our MAGDM method provides DEs, scientists, and practitioners a practical approach to make reasonable decisions. Second, our method permits the attribute values by several possible linguistic terms, which effectively handle DEs’ hesitancy. Therefore, our method is more practical and powerful than some existing decision-making methods. First, it is more useful than that proposed by Garg [31] based on LPFSs. Garg’s [31] MAGDM method only allows the MD and NMD of attribute values to be denoted by single linguistic terms, which overlooks DEs’ high hesitancy in complicated MAGDM situations. In addition, our method can solve decision-making problems in which attribute values are in the form of LPFSs. However, the decision-making method introduced by Garg [31] is unable to handle MAGDM problems in DHLPFSs. Additionally, our proposed method is also more powerful than that put forward by Yu et al.’s [62] based on DHFSs. Similar to DHLPFSs, DHFSs can also effectively deal with DEs’ high hesitancy in alternatives’ performance evaluation process. However, in DHFSs the possible MDs and NMDs are represented by crisp numbers while in DHLPFSs all MDs and NMDs are denoted by linguistic terms. In other words, DHFSs can only describe DEs’ quantitative evaluation values, while DHLPFSs depict both DEs’ quantitative and qualitative evaluation information. Hence, our method is also better than Yu et al.’s [62] MAGDM method. We provide Table 7 to better illustrate the advantages of our proposed method.
4 Probabilistic Dual Hesitant Linguistic Pythagorean Fuzzy Sets and Their Applications
In this section, we introduce another new concept, called PDHLPFSs, for depicting DEs’ evaluation information. We first introduce the motivations of proposing PDHLPFSs. Then, the definition of PDHLPFSs, as well as some other notions, such as operational rules, comparison method, and AOs are studied. Based on these notions, a new MAGDM method is proposed and its actual performance in realistic decision-making problems is illustrated through numerical examples.
4.1 Motivations of Proposing PDHLPFSs
As discussed above, DHLPFSs permit multiple linguistic MDs and NMDs, which can more effectively describe DEs’ evaluation values. However, as realistic MAGDM problems and very complicated, there are quite a few situations that cannot be handled by DHLPFSs. In DHLPFSs, all possible values provided by DEs have importance, which is not consistent with real decision-making situations. Actually, each member in DHLPFEs has a different degree of importance. We provide the following examples to better explain the drawbacks of DHLPFSs.
Example 6
A professor is invited to evaluate the innovation of a student’s thesis (which can be denoted as A for convenience). Let S = {s0 = very poor, s1 = poor, s2 = slightly poor, s3 = fair, s4 = slightly good, s5 = good, s6 = slightly good} be a pre-defined linguistic term set. The professor may express that he/she is 30% sure that the MD should be s4, and 70% sure that the MD should be s5. In addition, he/she is 40% sure that the NMD should be s0, 40% and 20% sure that the NMD should be s2 and s3, respectively. Then the evaluation value of the expert can be expressed as
Example 7
There are a hundred teachers and students and they are required to express how they feel about the satisfied degree of the design scheme of new campus (which can be denoted as B convenience). Let S = {s0 = very poor, s1 = poor, s2 = slightly poor, s3 = fair, s4 = slightly good, s5 = good, s6 = slightly good} be a pre-defined linguistic term set. For the MDs, 28 of them state it should be s3, 34 of them argue it should be s4, and the other 38insist it should be s5. For the NMDs, 57 of them state it should be s1 and the other 42 of them insist it should be s3. Then the overall evaluation value can be expressed as
The above examples reveal that in order to more accurately capture DEs’ evaluation values, not only multiple MDs and NMDs but also their corresponding probabilistic information should be taken into account. As a matter of fact, some scholars have noticed this phenomenon and some effective information description tools have been proposed, such as probabilistic linguistic sets, probabilistic hesitant fuzzy sets, and probabilistic dual hesitant fuzzy sets. Motivated by these fuzzy set theories, we genialize DHLPFSs into PDHLPFSs.
4.2 Definition of PDHLPFSs
Definition 9
Let X be a fixed set and \(\tilde{S} = \left\{ {s_{\alpha } \left| {0 \le \alpha \le l} \right.} \right\}\) be continuous linguistic term set with odd cardinality. A probabilistic dual hesitant linguistic Pythagorean fuzzy set (PDHLPFSs) E is expressed as
The component \(h_{E} \left( x \right)|p\left( x \right)\) and \(g_{E} \left( x \right)|t\left( x \right)\) are two sets of some possible values, where \({ }h_{E} \left( x \right),g_{E} \left( x \right) \subseteq \tilde{S}\), denoting the possible linguistic MDs and NMDs of the element \(x \in X\) to the set E, respectively, such that \(\sigma^{q} + \eta^{q} \le l^{q} \left( {q \ge 1} \right)\), where \(s_{\sigma } \in h_{E} \left( x \right)\), and \(s_{\eta } \in g_{E} \left( x \right)\) for \(x \in X\). \(p\left( x \right)\) and t(x) are corresponding probabilistic information of \(h_{E} \left( x \right)\) and \(g_{E} \left( x \right)\), respectively, such that \(0 \le p_{i} \le 1\), \(0 \le t_{j} \le 1\), \(\sum\nolimits_{i = 1}^{\# h} {p_{i} } = 1\), and \(\sum\nolimits_{j = 1}^{\# g} {t_{j} } = 1\). For convenience, we call the ordered paper \(e\left( x \right) = \left( {h_{E} \left( x \right)\left| {p\left( x \right),g_{E} \left( x \right)} \right|t\left( x \right)} \right)\) a probabilistic dual hesitant linguistic Pythagorean fuzzy element (PDHLPFE), which can be denoted as \(e = \left( {h\left| {p,g} \right|t} \right)\) for simplicity.
From Definition 9, it is seen that PDHLPFS is a generalized form of DHLPFS and DHLPFS is a special case of PDHLPFS, where the importance degrees of all members are equal. In the framework of PDHLPFSs, the overall evaluation value of DEs’ in Example 1 can be express as d = {{s1 | 0.125, s2 | 0.250, s3 | 0.125, s4 | 0.375, s5 | 0.125}, {s0 | 0.250, s1 | 0.125, s2 | 0.250, s3 | 0.375}}, which is a PDHLPFE.
4.3 Operation of PDHLPFEs
Definition 10
Let \( e_{1} = \left( {h_{1} \left| {p_{{h_{1} }} ,g_{1} } \right|t_{{g_{1} }} } \right)\), \(e_{2} = \left( {h_{2} \left| {p_{{h_{2} }} ,g_{2} } \right|t_{{g_{2} }} } \right)\), and \(e = \left( {h\left| {p,g} \right|t} \right)\) be any three PDHLPFEs and \(\lambda\) be a positive real number,
-
(5)
\(e_{1} \oplus e_{2} = \bigcup\nolimits_{{\sigma_{1} \in h_{1} ,\sigma_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} {\left\{ {\left\{ {s_{{\left( {\sigma_{1}^{2} + \sigma_{2}^{2} - \sigma_{1}^{2} \sigma_{2}^{2} /l^{2} } \right)^{1/2} }} |p_{{\sigma_{1} }} p_{{\sigma_{2} }} } \right\},\left\{ {s_{{\left( {\eta_{1} \eta_{2} /l} \right)}} |t_{{\eta_{1} }} t_{{\eta_{2} }} } \right\}} \right\}}\);
-
(6)
\(e_{1} \otimes e_{2} = \bigcup\nolimits_{{\sigma_{1} \in h_{1} ,\sigma_{2} \in h_{2} ,\eta_{1} \in g_{1} ,\eta_{2} \in g_{2} }} {\left\{ {\left\{ {s_{{\left( {\sigma_{1} \sigma_{2} /l} \right)}} |p_{{\sigma_{1} }} p_{{\sigma_{2} }} } \right\},\left\{ {s_{{\left( {\eta_{1}^{2} + \eta_{2}^{2} - \eta_{1}^{2} \eta_{2}^{2} /l^{2} } \right)^{1/2} }} |t_{{\eta_{1} }} t_{{\eta_{2} }} } \right\}} \right\}}\);
-
(7)
\(\lambda e = \bigcup\nolimits_{\sigma \in h,\eta \in g} {\left\{ {\left\{ {s_{{l\left( {1 - \left( {1 - \sigma^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} |p_{\sigma } } \right\},\left\{ {s_{{l\left( {\eta /l} \right)^{\lambda } }} |t_{\eta } } \right\}} \right\}}\);
-
(8)
\(e^{\lambda } = \bigcup\nolimits_{\sigma \in h,\eta \in g} {\left\{ {\left\{ {s_{{l\left( {\sigma /l} \right)^{\lambda } }} |p_{\sigma } } \right\},\left\{ {s_{{l\left( {1 - \left( {1 - \eta^{2} /l^{2} } \right)^{\lambda } } \right)^{1/2} }} |t_{\eta } } \right\}} \right\}}\).
Example 8
Let \(e_{1} = \left\{ {\left\{ {s_{3} \left| {0.5,s_{4} } \right|0.2,s_{5} |0.3} \right\},\left\{ {s_{2} \left| {0.6,s_{3} } \right|0.4} \right\}} \right\}\) and \(e_{2} = \left\{ {\left\{ {s_{2} \left| {0.3,s_{4} } \right|0.7} \right\},\left\{ {s_{4} |1} \right\}} \right\}\) be two PDHLPFEs defined on a pre-given continuous linguistic set \(\tilde{S} = \left\{ {s_{\alpha } \left| {0 \le \alpha \le 6} \right.} \right\}\), then
Theorem 8
Let \(e_{1} = \left( {h_{1} \left| {p_{{h_{1} }} ,g_{1} } \right|t_{{g_{1} }} } \right)\) , \(e_{2} = \left( {h_{2} \left| {p_{{h_{2} }} ,g_{2} } \right|t_{{g_{2} }} } \right)\) , and \(e = \left( {h\left| {p,g} \right|t} \right)\) be any three PDHLPFEs, then
-
(1)
\(e_{1} \oplus e_{2} = e_{2} \oplus e_{2}\);
-
(2)
\(e_{1} \otimes e_{2} = e_{2} \otimes e_{1}\);
-
(3)
\(\lambda \left( {e_{1} \oplus e_{2} } \right) = \lambda e_{1} \oplus \lambda e_{2}\);
-
(4)
\(\lambda_{1} e \oplus \lambda_{2} e = \left( {\lambda_{1} + \lambda_{2} } \right)e,\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right)\);
-
(5)
\(e^{{\lambda_{1} }} \otimes e^{{\lambda_{2} }} = e^{{\lambda_{1} + \lambda_{2} }} ,\left( {\lambda_{1} ,\lambda_{2} \ge 0} \right)\);
-
(6)
\(e_{1}^{\lambda } \otimes e_{2}^{\lambda } = \left( {e_{1} \otimes e_{2} } \right)^{\lambda } ,\left( {\lambda \ge 0} \right)\).
Proof It is easy to prove that (1) and (2) hold. In the following, we try to prove the correctness of the following equations. According to the operational rules for PDHLPFEs presented in Definition 10, we have
and
which proves that (3) holds.
Meanwhile, we can obtain that
and
which illustrates the validity of (4).
Moreover,
and
Hence, (5) holds.
Finally,
and
which demonstrates the correctness of (6).
4.4 Comparison Method of PDHLPFEs
Definition 11
Let \( e = \left( {h\left| {p,g} \right|t} \right)\) be a PDHLPFEs, the score function \(\Gamma \left( e \right)\) of e is expressed as
and the accuracy function \(\Omega \left( e \right)\) is defined as
where #h and #g denote the numbers of elements in h and g. For any two PDHLPFEs e1 and e2, then
-
(1)
If \(\Gamma \left( {e_{1} } \right) >\Gamma \left( {e_{2} } \right)\), then \(e_{1} > e_{2}\);
-
(2)
If \(\Gamma \left( {e_{1} } \right) =\Gamma \left( {e_{2} } \right)\), then
If \(\Omega \left( {e_{1} } \right) >\Omega \left( {e_{2} } \right)\), then \(e_{1} > e_{2}\);
If \(\Omega \left( {e_{1} } \right) =\Omega \left( {e_{2} } \right)\), then \(e_{1} = e_{2}\).
Example 9
Let \(\tilde{S} = \left\{ {s_{\alpha } |0 \le \alpha \le 6} \right\}\) be a pre-defined continuous linguistic term set, and \(e_{1} = \left\{ {\left\{ {s_{0} \left| {0.2,s_{2} } \right|0.3,s_{3} |0.5} \right\},\left\{ {s_{4} \left| {0.4,s_{5} } \right|0.6} \right\}} \right\}\) and \(e_{2} = \left\{ {\left\{ {s_{1} \left| {0.5,s_{3} } \right|0.5} \right\},\left\{ {s_{2} \left| {0.2,s_{3} } \right|0.7,s_{5} |0.1} \right\}} \right\}\) be two PDHLPFEs defined on \(\tilde{S}\), then we have
According to Definition 11, we can get \(e_{2} > e_{1}\).
4.5 Aggregation Operators of PDHLPFEs
Definition 12
Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of PDHLPFEs and \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\) be the weight vector, such that \(0 \le w_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). The probabilistic dual hesitant linguistic Pythagorean fuzzy weighted average (PDHLPFWA) operator is expressed as
Theorem 9
Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be collection of PDHLPFEs, then the aggregation result by using the PDHLPFWA operator is also a PDHLPFEs and
Proof We first prove that (24) holds for n = 2. Since
and
Then
which demonstrates that Eq. (24) holds for n = 2.
If Eq. (24) holds for n = k, i.e.,
then when n = k + 1, we can obtain
i.e., Eq. (24) holds for n = k + 1. Therefore, Eq. (24) holds for all n. The proof of Theorem 9 is completed.
Theorem 10
(Monotonicity) Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\) and \(e_{i}^{*} = \left( {h_{i}^{*} \left| {p_{{h_{i}^{*} }} ,g_{i}^{*} } \right|t_{{g_{i}^{*} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be two collections of PDHLPFEs, where \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) and \(s_{{\sigma_{i}^{*} }} \in h_{i}^{*}\), \(s_{{\eta_{i}^{*} }} \in g_{i}^{*} .\) For \(\forall i = 1,2, \ldots ,n\), if \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\), while the probabilities are the same, i.e., \(p_{{\sigma_{i} }} = p_{{\sigma_{i}^{*} }}\),\(t_{{\eta_{i} }} = t_{{\eta_{i}^{*} }}\), then
Proof For any \(i\), there are \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\). For the terms in the aggregated results, we have
According to the score function in Definition 11, we can get \(PDHLPFWA\left( {e_{1} ,e_{2} , \ldots ,e_{n} } \right) \le PDHLPFWA\left( {e_{1}^{*} ,e_{2}^{*} , \ldots ,e_{n}^{*} } \right) \) with equality if and only if \(s_{{\sigma_{i} }} = s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} = s_{{\eta_{i}^{*} }}\) for all \(i\).
Theorem 11
(Boundedness) Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of PDHLPFEs. For each \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\)(\(i = 1,2, \ldots ,n\)), let \(e^{ - } = \left( {s_{{{\text{min}}\{ \sigma_{i} \} }} \left| {p_{{{\text{min}}\left\{ {\sigma_{i} } \right\}}} ,s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right|t_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right)\), \(e^{ + } = \left( {s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}} \left| {p_{{{\text{max}}\{ \sigma_{i} \} }} ,s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right|t_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right)\). Then
Proof For \(\forall i = 1,2, \ldots ,n\), we have \(s_{{{\text{min}}\{ \sigma_{i} \} }} \le s_{{\sigma_{i} }} \le s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}}\), \(s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} \le s_{{\eta_{i} }} \le s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}}\), \(p_{{{\text{min}}\left\{ {\sigma_{i} } \right\}}} \le p_{{\sigma_{i} }} \le p_{{{\text{max}}\{ \sigma_{i} \} }}\), \(t_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} \le t_{{\eta_{i} }} \le t_{{{\text{max}}\left\{ {\eta_{i} } \right\}}}\). Then
For the probabilities:
and
And,
According to the score function in Definition 11, we have \(PDHLPFWA\left( {e_{1} ,e_{2} , \ldots ,e_{n} } \right) \ge PDHLPFWA\left( {e^{ - } ,e^{ - } , \ldots ,e^{ - } } \right)\) with equality if and only if \(e_{i}\) is same as \(e^{ - }\). Similarly, \(PDHLPFWA\left( {e_{1} ,e_{2} , \ldots ,e_{n} } \right) \le PDHLPFWA\left( {e^{ + } ,e^{ + } , \ldots ,e^{ + } } \right)\) with equality if and only if \(e_{i}\) is same as \(e^{ + }\) can be obtained. So, the proof of the theorem is completed.
Definition 13
Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of PDHLPFEs and \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\) be the weight vector, such that \(0 \le w_{i} \le 1\) and \(\sum\nolimits_{i = 1}^{n} {w_{i} } = 1\). The probabilistic dual hesitant linguistic Pythagorean fuzzy weighted geometric (PDHLPFWG) operator is expressed as
Theorem 12
Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be collection of PDHLPFEs, then the aggregation result by using the PDHLPFWG operator is also a PDHLPFEs and
The proof of Theorem 12 is similar to that of Theorem, which is omitted here. In addition, it is easy to prove that PDHLPFWG operator has the following properties.
Theorem 13
(Monotonicity) Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\) and \(e_{i}^{*} = \left( {h_{i}^{*} \left| {p_{{h_{i}^{*} }} ,g_{i}^{*} } \right|t_{{g_{i}^{*} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be two collections of PDHLPFEs, where \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\) and \(s_{{\sigma_{i}^{*} }} \in h_{i}^{*}\), \(s_{{\eta_{i}^{*} }} \in g_{i}^{*} .\) For \(\forall i = 1,2, \ldots ,n\), if \(s_{{\sigma_{i} }} \le s_{{\sigma_{i}^{*} }}\) and \(s_{{\eta_{i} }} \ge s_{{\eta_{i}^{*} }}\), while the probabilities are the same, i.e., \(p_{{\sigma_{i} }} = p_{{\sigma_{i}^{*} }}\),\(t_{{\eta_{i} }} = t_{{\eta_{i}^{*} }}\), then
Theorem 14
(Boundedness) Let \(e_{i} = \left( {h_{i} \left| {p_{{h_{i} }} ,g_{i} } \right|t_{{g_{i} }} } \right)\left( {i = 1,2, \ldots ,n} \right)\) be a collection of PDHLPFEs. For each \(s_{{\sigma_{i} }} \in h_{i}\), \(s_{{\eta_{i} }} \in g_{i}\)(\(i = 1,2, \ldots ,n\)), let \(e^{ - } = \left( {s_{{{\text{min}}\{ \sigma_{i} \} }} \left| {p_{{{\text{min}}\left\{ {\sigma_{i} } \right\}}} ,s_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right|t_{{{\text{max}}\left\{ {\eta_{i} } \right\}}} } \right)\), \(e^{ + } = \left( {s_{{{\text{max}}\left\{ {\sigma_{i} } \right\}}} \left| {p_{{{\text{max}}\{ \sigma_{i} \} }} ,s_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right|t_{{{\text{min}}\left\{ {\eta_{i} } \right\}}} } \right)\). Then,
4.6 MAGDM Based on PDHLPFEs
In this section, we introduce a new MAGDM method under PDHLPFSs based on the proposed AOs. Further, a numerical example is presented to show the effectiveness of our proposed method.
4.6.1 The Main Steps of a MAGDM Approach Under PDHLPFSs
A representative probabilistic dual hesitant linguistic Pythagorean fuzzy MAGDM problem is described as follows: Let \(A = \left\{ {A_{1} ,A_{2} , \ldots ,A_{m} } \right\}\) be a set of candidates and \(G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{n} } \right\}\) be set of attributes. The weight vector of attributes is \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\), such that \(\sum\nolimits_{j = 1}^{n} {w_{j} } = 1\) and \(0 \le w_{j} \le 1\). Several DEs \(D = \left\{ {D_{1} ,D_{2} , \ldots ,D_{t} } \right\}\) are invited to form a group to evaluate the efficiency of all the feasible alternatives. The weight vector of DEs is \(\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{t} } \right)^{T}\), such that \(0 \le \lambda_{e} \le 1\) and \(\sum\nolimits_{e = 1}^{t} {\lambda_{e} } = 1\). Let \(\tilde{S} = \left\{ {s_{h} \left| {h \in \left[ {0,l} \right]} \right.} \right\}\) be a pre-defined continuous linguistic term set. For attribute \(G_{j} \left( {j = 1,2, \ldots ,n} \right)\) of alternative \(A_{i} \left( {i = 1,2, \ldots ,m} \right)\), the DE \(D_{k} \left( {k = 1,2, \ldots ,t} \right)\) uses a PDHLPFE \(e_{ij}^{k} = \left( {h_{ij}^{k} \left| {p_{{h_{ij}^{k} }} } \right.,g_{ij}^{k} \left| {t_{{g_{ij}^{k} }} } \right.} \right)\) to express his/her evaluation. Finally, a set of probabilistic dual hesitant linguistic Pythagorean fuzzy decision matrices are gotten. In the following, we use the proposed AOs to introduce a novel MAGDM method.
4.6.2 The Steps of a Novel MAGDM Method Based on PDHLPFEs
Step 1. Normalize the original decision matrix. In most practical MAGDM problems, there are two types of attributes, i.e., benefit type and cost type. Hence, the original decision matrices should be normalized according to the following formula:
Step 2. Compute the overall decision matrix. For alternative \(A_{i} \left( {i = 1,2, \ldots ,m} \right)\), use the PDHLPFWA operator
or the PDHLPFWG operator
to determine the comprehensive evaluation matrix.
Step 3. Compute the final overall evaluation values of alternatives. For alternative \(A_{i} \left( {i = 1,2, \ldots ,m} \right)\), use the PDHLPFWA operator
or the PDHLPWG operator
to compute its comprehensive evaluation value.
Step 4. Calculate the score value \(S\left( {e_{i} } \right)\) and accuracy value \(H\left( {e_{i} } \right)\) of \(e_{i}\).
Step 5. Rank all the alternatives according to the score and accuracy values.
4.6.3 A Real Application of the Proposed Method
Example 10
In order to stimulate the enthusiasm for research of doctoral students, a college plans to evaluate the quality of doctoral students’ theses and selects the best one and gives the author scholarship. After primary selection, there are five theses authored by five students, and three professors are required to evaluate the five theses. The weight vector of the three professors is \(\lambda = \left( {0.243,0.514,0.243} \right)^{T}.\) The five theses are assessed under four attributes, i.e., the significant degree of the study (G1), the degree of innovation (G2), the degree of compliance with academic norms (G3), and the significant degree methodology (G4). The weight vector of attributes is \(w = \left( {0.3,0.1,0.2,0.4} \right)^{T}\). Let S = {s0 = extremely poor, s1 = very poor, s2 = poor, s3 = slightly poor, s4 = fair, s5 = slightly good, s6 = good, s7 = very good, s8 = extremely good} be a linguistic term set, and DEs use PDHLPFEs to express their evaluation values. The original decision matrices are presented in Tables 8, 9, 10.
Step 1. As the original decision matrices are benefit types, the original decision matrices do not need to be normalized.
Step 2. Use the PDHLPFWA operator to determine the comprehensive decision matrix, and the result is listed in Table 11.
Step 3. Use the PDHLPFWA operator to calculate the overall evaluation values of alternatives. As the comprehensive evaluations are too complicated, we omit them here.
Step 4. Calculate the score values of alternatives, we can obtain
Step 5. Rank the alternatives and we can get \(A_{2} \succ A_{4} \succ A_{1} \succ A_{3}\), which implies A2 is the optimal alternative.
If we calculate the comprehensive decision matrix and overall evaluation values by the PDHLPFWG operator, then the score values of alternatives are \(\Gamma \left( {e_{1} } \right) = s_{5.6266}\), \(\Gamma \left( {e_{2} } \right) = s_{5.6583}\), \(\Gamma \left( {e_{3} } \right) = s_{5.5646}\), and \(\Gamma \left( {e_{4} } \right) = s_{5.6453}\), and the ranking order is \(A_{2} \succ A_{4} \succ A_{1} \succ A_{3}\), which indicates A2 is the best alternative.
4.6.4 Further Discussion
This section proposes a novel MAGDM method wherein DEs’ evaluation information or attribute values are expressed by PDHLPFSs. To sum up, the main advantages of our proposed decision-making method have three aspects. First, it employs linguistic terms to denote the possible MDs and NMDs, which makes it easy to denote DEs’ assessment information both quantificationally and qualitatively. Second, it allows the existence of multiple MDs and NMDs, which is more capable of describing DEs’ high hesitancy in realistic complex decision-making problems. Third, it can also describe probabilistic information of each linguistic term, making it smoother to describe a decision-making group’s overall evaluation information. These three merits make our decision-making method more flexible and powerful. In addition, our MAGDM method is also more powerful than some existing decision-making approaches. First, compared with aforementioned decision-making method based on DHLPFSs, the newly developed MAGDM method under PDHLPFSs can more accurately depict DEs’ evaluation information, as it not only considers multiple MDs and NMDs but also take the probabilistic values of MDs and NMDs into consideration. Second, it is also more powerful than the method introduced by Hao et al. [55]. It is noted that the method proposed by Hao et al. [55] is based on PDHFSs, which use crisp numbers to denote the possible MDs and NMDs. Hence, Hao et al.’s [55] method only consider DEs’ quantitative evaluation values. In our proposed PDHLPFSs, the possible MDs and NMDs are denoted by linguistic terms, and hence our method can describe DEs’ evaluation values both quantificationally and qualitatively. We provide Table 12 to better demonstrate the advantages of our developed MAGDM method.
5 Conclusion Remarks
The LPFSs can effectively describe DEs’ evaluation values in complicated decision-making situations. However, the main drawbacks of LPFSs are they overlook multiple MDs and NMDs as well as their corresponding probabilistic information. The aim is to overcome the two shortcomings by probing extensions of LPFSs. We first proposed the DHLPFSs, which have the ability of effectively dealing with multiple MDs and NMDs. After it, we proposed AOs for DHLPFSs and applied in MAGDM method. we continued to consider the fact that members in DHLPFSs may have different frequencies, occurrences, and degrees of importance, we further generalize DHLPFSs to PDHLPFSs by considering not multiple MDs and NMDs but also their probabilities. We further showed how to use to PDHLPFSs to solve practical MAGDM problems. Numerical examples have demonstrated the effectiveness of our proposed novel MAGDM methods. In future research, we shall continue our study from two aspects. First, we are studying applications of our methods in more actual-life MAGDM methods. Second, we will study more extensions of LPFSs, such as cubic LPFSs, hesitant LPFSs, uncertain LPFSs, etc., to accommodate more complex decision-making environments and propose novel MAGDM methods to aid practitioners to make wise decisions.
References
Garai T, Dalapati S, Garg H, Roy TK (2020) Possibility mean, variance and standard deviation of single-valued neutrosophic numbers and its applications to multi-attribute decision-making problems. Soft Comput. https://doi.org/10.1007/s00500-020-05112-2
Garg H, Ali Z, Mahmood T (2020) Algorithms for complex interval-valued q-rung orthopair fuzzy sets in decision making based on aggregation operators, AHP and TOPSIS. Expert Syst. https://doi.org/10.1111/exsy.12609
Riaz M, Davvaz B, Fakhar A, Firdous A (2020) Hesitant fuzzy soft topology and its applications to multi-attribute group decision-making. Soft Comput. https://doi.org/10.1007/s00500-020-04938-0
Naeem K, Riaz M, Peng XD, Afzal D (2019) Pythagorean fuzzy soft MCGDM methods based on TOPSIS, VIKOR and aggregation operators. J Intell Fuzzy Syst 37:6937–6957. https://doi.org/10.3233/JIFS-190905
Riaz M, Hashmi MR (2019) Linear Diophantine fuzzy set and its applications towards multi-attribute decision making problems J. Intell. Intell Fuzzy Syst 37:5417–5439. https://doi.org/10.3233/JIFS-190550
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96. https://doi.org/10.1016/S0165-0114(86)80034-3
Xu Z (2007) Intuitionistic fuzzy aggregation operators. IEEE T Fuzzy Syst 15:1179–1187. https://doi.org/10.1109/TFUZZ.2006.890678
Xu Z, Yager RR (2011) Intuitionistic fuzzy Bonferroni means. IEEE T Syst Man Cy-s 41:568–578. https://doi.org/10.1109/TSMCB.2010.2072918
Xia M, Xu Z (2010) Generalized point operators for aggregating intuitionistic fuzzy information. J Intel Syst 25:1061–1080. https://doi.org/10.1002/int.20439
Qin J, Liu X (2014) An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J Intel Fuzzy Syst 27:2177–2190. https://doi.org/10.3233/IFS-141182
Liu P, Li D (2017) Some Muirhead mean operators for intuitionistic fuzzy numbers and their applications to group decision making. PLOS ONE 12(1). https://doi.org/10.1371/journal.pone.0168767
Xu Z (2011) Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators. Knowl-Based Syst 24:749–760. https://doi.org/10.1016/j.knosys.2011.01.011
He Y, He Z, Deng Y, Zhou P (2016) IFPBMS and their application to multiple attribute group decision making. J Oper Res Soc 67:127–147. https://doi.org/10.1057/jors.2015.66
Chen ZC, Liu PH, Pei Z (2015) An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int J Comput Int Syst 8:747–760. https://doi.org/10.1080/18756891.2015.1061394
Ou Y, Yi L, Zou B, Pei Z (2018) The linguistic intuitionistic fuzzy set TOPSIS method for linguistic multi-criteria decision makings. Int J Comput Int Syst 11:120–132. https://doi.org/10.2991/ijcis.11.1.10
Yuan R, Tang J, Meng F (2019) Linguistic intuitionistic fuzzy group decision making based on aggregation operators. Int J Fuzzy Syst 21:407–420. https://doi.org/10.1007/s40815-018-0582-4
Meng F, Tang J, Fujita H (2019) Linguistic intuitionistic fuzzy preference relations and their application to multi-criteria decision making. Inform Fusion 46:77–90. https://doi.org/10.1016/j.inffus.2018.05.001
Liu P, You X (2018) Some linguistic intuitionistic fuzzy Heronian mean operators based on Einstein T-norm and T-conorm and their application to decision-making. J Intell Fuzzy Syst 35:2433–2445. https://doi.org/10.3233/jifs-18032
Liu P, Qin X (2017) Power average operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision making. J Intell Fuzzy Syst 32:1029–1043. https://doi.org/10.3233/JIFS-16231
Liu P, Qin X (2017) Maclaurin symmetric mean operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision-making. J Exp Theor Artif 29:1173–1202. https://doi.org/10.1080/0952813X.2017.1310309
Liu P, Liu X (2019) Linguistic intuitionistic fuzzy hamy mean operators and their application to multiple-attribute group decision making. IEEE Access, 127728–127744. https://doi.org/10.1109/access.2019.2937854
Liu P, Liu J, Merigo JM (2018) Partitioned Heronian means based on linguistic intuitionistic fuzzy numbers for dealing with multi-attribute group decision making. Appl Soft Comput 62:395–422. https://doi.org/10.1016/j.asoc.2017.10.017
Garg H, Kumar K (2019) Multiattribute decision making based on power operators for linguistic intuitionistic fuzzy set using set pair analysis. Expert Syst 36. https://doi.org/10.1111/exsy.12428
Zhang H, Peng H, Wang J, Wang J (2017) An extended outranking approach for multi-criteria decision-making problems with linguistic intuitionistic fuzzy numbers. Appl Soft Comput 59:462–474. https://doi.org/10.1016/j.asoc.2017.06.013
Peng H, Wang J (2017) Cloud decision model for selecting sustainable energy crop based on linguistic intuitionistic information. Int J Syst Sci 48:3316–3333. https://doi.org/10.1080/00207721.2017.1367433
Garg H, Kumar K (2018) Group decision making approach based on possibility degree measures and the linguistic intuitionistic fuzzy aggregation operators using Einstein norm operations. Soft Comput 31:175–209
Rong Y, Liu Y, Pei Z (2020) Novel multiple attribute group decision-making methods based on linguistic intuitionistic fuzzy information. Mathematics. https://doi.org/10.3390/math8030322
Liu P, Liu X, Ma G, Liang Z, Wang C, Alsaadi FE (2020) A multi-attribute group decision-making method based on linguistic intuitionistic fuzzy numbers and Dempster-Shafer evidence theory. Int. J. Inf. Tech. Decis. https://doi.org/10.1142/s0219622020500042
Arora R, Garg H (2019) Group decision-making method based on prioritized linguistic intuitionistic fuzzy aggregation operators and its fundamental properties. Comput Appl Math 38:36. https://doi.org/10.1007/s40314-019-0764-1
Garg H, Kumar K (2018) Some aggregation operators for linguistic intuitionistic fuzzy set and its application to group decision-making process using the set pair analysis. Arab J Sci Eng 43:3213–3227. https://doi.org/10.1007/s13369-017-2986-0
Garg H (2018) Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int J Intel Syst 33:1234–1263. https://doi.org/10.1002/int.21979
Yager RR (2014) Pythagorean membership grades in multi-criteria decision making. IEEE T Fuzzy Syst 22:958–965. https://doi.org/10.1109/TFUZZ.2013.2278989
Akram M, Garg H, Zahid K (2020) Extensions of ELECTRE-I and TOPSIS methods for group decision-making under complex Pythagorean fuzzy environment. Iran J Fuzzy Syst. https://doi.org/10.22111/IJFS.2020.5363
Jan N, Aslam M, Ullah K, Mahmood T, Wang J (2019) An approach towards decision making and shortest path problems using the concepts of interval-valued Pythagorean fuzzy information. Int J Intel Syst 34: 2403–2428. https://doi.org/10.1002/int.22154
Garg H (2019) Neutrality operations-based Pythagorean fuzzy aggregation operators and its applications to multiple attribute group decision-making process. J Amb Intel Hum Comp 11:1–21. https://doi.org/10.1007/s12652-019-01448-2
Zhu X, Bai K, Wang J, Zhang R, Xing Y (2019) Pythagorean fuzzy interaction power partitioned Bonferroni means with applications to multi-attribute group decision making. J Intel Fuzzy Syst 36:3423–3438. https://doi.org/10.3233/jifs-181171
Garg H (2019) Novel neutrality operation–based Pythagorean fuzzy geometric aggregation operators for multiple attribute group decision analysis. Int J Intel Syst 34:2459–2489. https://doi.org/10.1002/int.22157
Xing Y, Zhang R, Wang J, Zhu X (2018) Some new Pythagorean fuzzy Choquet-Frank aggregation operators for multi-attribute decision making. Int J Intel Syst 33:2189–2215. https://doi.org/10.1002/int.22025
Akram M, Ilyas F, Garg H (2020) Multi-criteria group decision making based on ELECTRE I method in Pythagorean fuzzy information. Soft Comput 24:3425–3453. https://doi.org/10.1007/s00500-019-04105-0
Li L, Zhang R, Wang J, Zhu X, Xing Y (2018) Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J Intel Fuzzy Syst 35:2035–2050. https://doi.org/10.3233/jifs-171907
Garg H (2019) Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision-making process. Int J Intel Syst 34:601–626. https://doi.org/10.1002/int.22067
Ma X, Akram M, Zahid K, Alcantud JCR (2020) Group decision-making framework using complex Pythagorean fuzzy information. Neural Comput. Appl. https://doi.org/10.1007/s00521-020-05100-5
Liu Y, Qin Y, Xu L, Liu H, Liu J (2019) Multiattribute group decision-making approach with linguistic Pythagorean fuzzy information. IEEE Access 7:143412–143430. https://doi.org/10.1109/access.2019.2945005
Han Q, Li W, Lu Y, Zhang M, Quan Q, Song Y (2020) TOPSIS method based on novel entropy and distance measure for linguistic pythagorean fuzzy sets with their application in multiple attribute decision making. IEEE Access 8:14401–14412. https://doi.org/10.1109/access.2019.2963261
Lin M, Wei J, Xu Z, Chen R (2018) Multiattribute group decision-making based on linguistic Pythagorean fuzzy interaction partitioned Bonferroni mean aggregation operators. Complexity 2018:1–24. https://doi.org/10.1155/2018/9531064
Torra V (2010) Hesitant fuzzy sets. J Intel Syst 25:529–539. https://doi.org/10.1002/int.20418
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zhu B, Xu Z, Xia M (2012) Dual hesitant fuzzy sets. J Appl Math 2012:1–13. https://doi.org/10.1155/2012/879629
Wei G, Lu M (2017) Dual hesitant Pythagorean fuzzy Hamacher aggregation operators in multiple attribute decision making. Arch Control Sci 27:365–395. https://doi.org/10.1515/acsc-2017-0024
Zhang S, Xu Z, He Y (2017) Operations and integrations of probabilistic hesitant fuzzy information in decision making. Inform Fusion 38:1–11. https://doi.org/10.1016/j.inffus.2017.02.001
Jiang F, Ma Q (2018) Multi-attribute group decision making under probabilistic hesitant fuzzy environment with application to evaluate the transformation efficiency. Appl Intel 48:953–965. https://doi.org/10.1007/s10489-017-1041-x
Song C, Xu Z, Zhao H (2018) A novel comparison of probabilistic hesitant fuzzy elements in multi-criteria decision making. Symmetry 10:177. https://doi.org/10.3390/sym10050177
Ding J, Xu Z, Zhao N (2017) An interactive approach to probabilistic hesitant fuzzy multi-attribute group decision making with incomplete weight information. J Intel Fuzzy Syst 32(3):2523–2536. https://doi.org/10.3233/JIFS-16503
Li J, Chen Q (2020) An outranking method for multicriteria decision making with probabilistic hesitant information. Expert Syst. https://doi.org/10.1111/exsy.12513
Hao Z, Xu Z, Zhao H, Zhan S (2017) Probabilistic dual hesitant fuzzy set and its application in risk evaluation. Knowl Based Syst 127:16–28. https://doi.org/10.1016/j.knosys.2017.02.033
Ren Z, Xu Z, Wang H (2019) The strategy selection problem on artificial intelligence with an integrated VIKOR and AHP method under probabilistic dual hesitant fuzzy information. IEEE Access 7:103979–103999. https://doi.org/10.1109/access.2019.2931405
Garg H, Kaur G (2018) Algorithm for probabilistic dual hesitant fuzzy multi-criteria decision-making based on aggregation operators with new distance measures. Mathematics. https://doi.org/10.3390/math6120280
Garg H, Kaur G (2020) Quantifying gesture information in brain hemorrhage patients using probabilistic dual hesitant fuzzy sets with unknown probability information. Comput Ind Eng 140: 106211. https://doi.org/10.1016/j.cie.2019.106211
Pang Q, Wang H, Xu Z (2016) Probabilistic linguistic term sets in multi-attribute group decision making. Inform Sci 369:128–143. https://doi.org/10.1016/j.ins.2016.06.021
Gong K, Chen C (2019) Multiple-attribute decision making based on equivalence consistency under probabilistic linguistic dual hesitant fuzzy environment. Eng Appl Artif Intel 85:393–401. https://doi.org/10.1016/j.engappai.2019.05.008
Şahin R, Altun F (2020) Decision making with MABAC method under probabilistic single-valued neutrosophic hesitant fuzzy environment. J Amb Intel Hum Comp 11:4195–4212. https://doi.org/10.1007/s12652-020-01699-4
Yu DJ, Zhang WY, Huang G (2016) Dual hesitant fuzzy aggregation operators. Technol Econ Dev Eco 22:194–209. https://doi.org/10.3846/20294913.2015.1012657
Acknowledgments
This work was supported by Funds for First-class Discipline Construction (XK1802-5).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
We declare that there is no conflict of interest with regard to the publication of this chapter.
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Wang, J., Shang, X., Xu, W., Ji, C., Feng, X. (2021). Extensions of Linguistic Pythagorean Fuzzy Sets and Their Applications in Multi-attribute Group Decision-Making. In: Garg, H. (eds) Pythagorean Fuzzy Sets. Springer, Singapore. https://doi.org/10.1007/978-981-16-1989-2_15
Download citation
DOI: https://doi.org/10.1007/978-981-16-1989-2_15
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-16-1988-5
Online ISBN: 978-981-16-1989-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)