Keywords

1 Introduction

Robotics is getting more and more popular in industrial field as it reduces manpower required for doing heavy jobs. Main types of robots used in industrial applications are “multiple-link manipulators” with different degrees of freedom. These kinds of robots can move according to their DOF and complete many tasks. Single-link manipulator model is made out of one fixed base, on which the whole system resides, a revolute joint and an arm, which can move freely on the x–y plane. DC motor or servomotors are mainly used to rotate the arms of manipulators. Here, a simple DC motor with high torque constant is used to move the arm of the manipulator. First, the dynamic model of that motor is designed [1]. Then, control logic is applied on the motor to move the arm to a specific angular position [2,3,4]. For tuning control parameters, simple tuning method is used [5]. Nowadays, in many industrial applications, rigid link manipulators cannot satisfy the needs. So, “Flexible link manipulators” have become an option. In comparison with rigid body manipulators, flexible manipulators have many advantages including higher efficiency, more flexibility, high load capacity, low energy consumption and larger application field. Flexible link manipulators have wide applications in aerospace engineering, precision instrument production, construction and many other fields [6]. With every practical system, there remains some uncertainty with the parameter values of that system. So, the control model needs to be more accurate to induce its controllability on those uncertain models. There are various control methods like “Robust control” or “Fractional control” methods to deal with parameter uncertainty or external disturbances [7] which are available for controlling these types of manipulators [8,9,10]. This paper also presents results of controlling an uncertain model of rigid body single-link manipulator. The stability of the system has been taken in account at the time of testing uncertain models.

This paper presents simulations of dynamic behavior of a rigid body single-link manipulator controlled by simple PID logic. PID control is a very popular control method applicable for controlling linear systems. By tuning its parameters, desired controlled output can be generated.

2 Mathematical Modeling of Single-Link Manipulator

The physical system consists of a fixed base, a DC motor and an arm. The arm is movable in x–y plane. Here, the arm acts as the “mechanical load” of the motor. The mathematical modeling of a single-link manipulator can be constructed by modeling the motor part, which is giving driving torque to the manipulator and then the arm part.

2.1 Transfer Function Model of the System

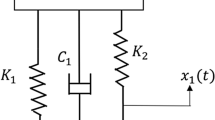
DC motor converts electrical energy into mechanical energy. It has a permanent magnet that produces magnetic field around the armature circuit. According to “Fleming’s Left-hand rule” that magnetic field along with the electric field of the armature inductance creates rotary motion of the rotor. When the motor spins with its full speed, a “Back EMF” is generated that decreases the applied armature voltage, which decreases the current flowing in the armature circuit. At points M1 and M2, mechanical load is connected. Figures 1 and 2 represent the armature circuit of DC motor and diagram of single link manipulator respectively.

Fig. 1
figure 1

DC motor armature circuit

Full size image

Parameters:

  • $$ m = {\text{Mass}}\,{\text{of}}\,{\text{the}}\,{\text{arm}} $$
  • $$ g = {\text{Gravitational}}\,{\text{acceleration}} $$
  • $$ l = {\text{Length}}\,{\text{of}}\,{\text{the}}\,{\text{arm}} $$
  • $$ V = {\text{Applied}}\,{\text{armature}}\,{\text{voltage}}, $$
  • $$ i_{m} = {\text{Armature}}\,{\text{current}}, $$
  • $$ R_{m} = {\text{Armature}}\,{\text{resistance}}, $$
  • $$ L_{m} = {\text{Armature}}\,{\text{inductance}}, $$
  • $$ K_{b} = {\text{Back}}\,{\text{emf}}\,{\text{constant}}, $$
  • $$ \theta = {\text{Angular}}\,{\text{position}}\,{\text{of}}\,{\text{rotor}}, $$
  • $$ \dot{\theta } = {\text{Angular}}\,{\text{velocity}}\,{\text{of}}\,{\text{rotor}}, $$
  • $$ J = {\text{Rotor}}\,{\text{inertia}}, $$
  • $$ b = {\text{Motor}}\,{\text{friction}}\,{\text{constant}}, $$
  • $$ K_{T} = {\text{Motor}}\,{\text{torque}}\,{\text{constant}}, $$
  • $$ T_{m} = {\text{Torque}}\,{\text{produced}}\,{\text{by}}\,{\text{motor}} $$

Applying KVL to the armature circuit,

$$ V = L_{m} \frac{{di_{m} }}{dt} + K_{b} \dot{\theta } + R_{m} i_{m} $$
(1)

Taking Laplace transform of Eq. (1),

$$ \begin{aligned} V\left( s \right) & = L_{m} s.I_{m} \left( s \right) + K_{b} s.\theta \left( s \right) + R_{m} .I_{m} \left( s \right) \\ & = > V\left( s \right) = I_{m} \left( s \right)\left[ {R_{m} + L_{m} s} \right] + K_{b} s.\theta \left( s \right) \\ \end{aligned} $$

So,

$$ I_{m} \left( s \right) = \frac{{V\left( s \right) - K_{b} s.\theta \left( s \right)}}{{\left( {R_{m} + L_{m} s} \right)}} $$
(2)

Torque produced by rotor,

$$ T_{m} = K_{T} . i_{m} $$

Taking Laplace transform of it,

$$ T_{m} \left( s \right) = K_{T} . I_{m} \left( s \right) $$

Kinematics:

For the arm in Fig. 2,

$$ x = \frac{l}{2} \cos \theta $$
$$ y = \frac{l}{2} \sin \theta $$
Fig. 2
figure 2

Single-link manipulator

Full size image

Velocity along x and y axis is, respectively,

$$ v_{x} = \dot{x} = - \frac{l}{2}\dot{\theta }\sin \theta $$
$$ v_{y} = \dot{y} = \frac{l}{2}\dot{\theta }\cos \theta $$

Overall velocity of the arm is,

$$ v = \sqrt {v_{x}^{2} + v_{y}^{2} } = \frac{l}{2}\dot{\theta } $$

Now, the kinetic energy of the system,

$$ E_{k} = \frac{1}{2}\left( {mv^{2} + I\dot{\theta }^{2} } \right) = \frac{1}{6}ml^{2} \dot{\theta }^{2} $$

Potential energy of the system,

$$ E_{p} = \frac{1}{2}{\text{mgl}}\sin \theta $$

So, Lagrangian of the system is,

$$ {\mathcal{L}} = E_{k} - E_{p} = \frac{1}{6}{\text{ml}}^{2} \dot{\theta }^{2} - \frac{1}{2}{\text{mgl}}\sin \theta $$

From Lagrange equation for torque,

$$ \frac{d}{dt}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{\theta }}}} \right) - \frac{{\partial {\mathcal{L}}}}{\partial \theta } = T_{m} $$
$$ \frac{1}{3}ml^{2} \ddot{\theta } + \frac{1}{2}{\text{mlg}}\cos \theta = T_{m} $$
(3)

For linearization, assuming \(\theta\) is very small, \(\cos \theta \approx 1\).

So, Eq. (3) becomes,

$$ \begin{aligned} & \frac{1}{3}{\text{ml}}^{2} \ddot{\theta } + \frac{1}{2}{\text{mlg}}\theta + b\dot{\theta } = T_{m} \\ & \quad = > 2{\text{ml}}^{2} \ddot{\theta } + 6b\dot{\theta } + 3{\text{mlg}}\theta = 6T_{m} \\ \end{aligned} $$

where \(b\dot{\theta }\) = damping part from the driving motor.

Dynamic equation of the arm can be expressed as,

$$ J\ddot{\theta } + 6b\dot{\theta } + p\theta = 6T_{m} $$
(4)

where, \( J = 2{\text{ml}}^{2}\), \(p = 3{\text{mlg}}\).

Taking Laplace transform of Eq. (4),

$$ \begin{aligned} & \left\{ {Js^{2} \theta \left( s \right) - \theta \left( 0 \right) - \dot{\theta }\left( 0 \right)} \right\} + 6bs. \theta \left( s \right) + p\theta \left( s \right) \\ & \quad = 6T_{m} \left( s \right) = 6K_{T} .I_{m} \left( s \right) \\ & \quad = > \theta \left( s \right)\left[ {Js^{2} + 6bs + p} \right] = 6K_{T} .I_{m} \left( s \right) \\ & \quad = > I_{m} \left( s \right) = \frac{{\theta \left( s \right).\left[ {Js^{2} + 6bs + p} \right]}}{{6K_{T} }} \\ \end{aligned} $$
(5)

Comparing (2) and (5), transfer function \(Y\left( s \right)\) can be obtained,

$$ Y\left( s \right) = \frac{\theta \left( s \right)}{{V\left( s \right)}} = \frac{{6K_{T} }}{{\left[ {\left( {R_{m} + L_{m} s} \right)\left( {Js^{2} + 6bs + p} \right) + s.K_{b} .K_{T} } \right]}} $$
(6)

State-space form of the above system has been obtained as,

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \\ {i_{m} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ { - \frac{p}{J}} & {\frac{ - 6b}{J}} & {\frac{{6K_{T} }}{J}} \\ 0 & {\frac{{ - K_{b} }}{J}} & {\frac{{ - R_{m} }}{{L_{m} }}} \\ \end{array} } \right).\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \\ {i_{m} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\frac{1}{{L_{m} }}} \\ \end{array} } \right).V $$
(7)
$$ y = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right) \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \\ {i_{m} } \\ \end{array} } \right) $$

2.2 Uncertainty Modeling of the System

The system represented by the transfer function \(Y\left( s \right)\) cannot be considered as the practical system. Practical systems can have different uncertainties which can deviate the nature of the practical system from the ideal one. Such uncertainties come mainly from external disturbances or real parameter variations. Here, the components of the system have some variation or uncertainty in their parameter values. So, parameters like m, Rm and Lm contributing to the transfer function \(Y\left( s \right)\) have some uncertainty in their value. The practical parameters of the system can be written as:

\(m_{p} = m + \Delta_{m} ,\) \(R_{mp} = R_{m} + \Delta_{{R_{m} }}\), \(L_{mp} = L_{m} + \Delta_{{L_{m} }}\), \(b_{p} = b + \Delta_{b}\) where \(\Delta_{r}\) = uncertainty of the parameter “r” and \(r_{p}\) = practical value of the parameter “r.” So the explicit form of state-space equation of the uncertain single-link manipulator model becomes:

Finally, the transfer function of the system with uncertainty is given by,

$$ Y_{U} \left( s \right) = \frac{{6K_{T} }}{{\left[ {\left( {R_{{mp}} + L_{{mp}} s} \right)\left( {2m_{p} l^{2} s^{2} + 6bs + 3m_{p} gl} \right) + s.K_{b} .K_{T} } \right]}} $$
(8)

3 Controller Design

3.1 Block Diagram of Single-Link Manipulator Angular Position Closed-Loop System

The closed loop angular position control system for single link manipulator is shown in Fig. 3.

Fig. 3
figure 3

Single-link manipulator angular position closed-loop block diagram

Full size image

3.2 Implementing PID Control to the Nominal Manipulator System

The term PID stands for “Proportional Integral Derivative.” PID controllers are flexible, simple and easy to implement. By using proper optimization, PID controller can control and regulate time-domain response of wide range of processes. The time-domain equation of PID controller is as follows:

$$ {\varvec{u}}\left( {\varvec{t}} \right) = {\varvec{u}}_{{{\mathbf{bias}}}} + {\varvec{K}}_{{\varvec{p}}} {\varvec{e}}\left( {\varvec{t}} \right) + {\varvec{K}}_{{\varvec{i}}} \int {{\varvec{e}}\left( {\varvec{t}} \right)} {\varvec{dt}} + {\varvec{K}}_{{\varvec{d}}} \frac{{{\varvec{de}}\left( {\varvec{t}} \right)}}{{{\varvec{dt}}}} $$
(9)

where \(u\left( t \right)\) = controller output, \(u_{{{\text{bias}}}}\) = initial value of controlled output (let \( u_{{{\text{bias}}}}\) = 0 for this case), \(e\left( t \right)\) = error term, i.e., difference between set point (SP) and process variable (PV), \(K_{p}\) = proportional gain, \(K_{i} = \frac{{K_{p} }}{{\tau_{i} }}\) (\(\tau_{i}\) is integral time constant), and \(K_{d} = K_{p} \tau_{d}\) (\(\tau_{d}\) is derivative time constant). Figure 4 shows the closed loop angular position control system with PID controller.

Laplace transforming (8),

$$ U\left( s \right) = E\left( s \right)\left[ {K_{p} + \frac{{K_{i} }}{{\text{s}}} + K_{d} {\text{s}}} \right] $$

Control transfer function,

$$ C\left( s \right) = \frac{U\left( s \right)}{{E\left( s \right)}} = K_{p} + \frac{{K_{i} }}{{\text{s}}} + K_{d} {\text{s}} $$

So, the overall open-loop transfer function of the controlled model becomes (Fig. 4),

$$ G\left( s \right) = Y\left( s \right).C\left( s \right) $$
Fig. 4
figure 4

Block diagram of PID control in single-link manipulator for controlling angular position

Full size image

Tuning PID parameters: To get desired response, the control parameters like \(K_{p}\), \(K_{i}\) and \(K_{d} \) should be tuned properly. By checking the output response plot, it can be pointed out values of which parameters should be increased or decreased. Table 1 shows the same.

Table 1 Tuning PID parameters
Full size table

4 Implementation of Proposed Controller in Python

Python, as an object-oriented programming language, is simple and versatile. All the simulations presented in this paper have been done in Python language. For simulating system response in different control environments, Python’s dedicated control system library is used [11]. For some mathematical purposes, different available modules are used. All the programming has been done using “Anaconda Navigator” and “Jupyter Notebook.”

Anaconda is an open-source software which directly comes with different Python and R language IDEs or platforms preinstalled. Anaconda is best used for machine learning and data analysis tasks. The software also comes with common modules and libraries installed but Anaconda’s Python package does not include control system library by default, so that it is need to be installed first using “Anaconda Prompt.” By writing “pip install control” command in the prompt, the library can be installed easily as shown in Fig. 5.

Fig. 5
figure 5

Installing control system library in Anaconda

Full size image

Then, after opening Anaconda Navigator, Jupyter notebook is to be selected, and it will automatically open Jupyter notebook in the browser at predefined path. There is also another Python IDE “Spyder” is available. Anaconda makes Jupyter notebook and Spyder databases interconnected, so anyone can easily switch in between them. The following figure shows the Anaconda Navigator and Jupyter notebook interface. Figures 6 and 7 show the navigator and editor interface respectively.

Fig. 6
figure 6

Launching Jupyter notebook from Anaconda Navigator

Full size image
Fig. 7
figure 7

Jupyter notebook interface

Full size image

Jupyter notebook is preferable for testing programs as it allows users to run different sections of program at any time. So, it is easy to find errors in the code.

Python control systems library is a Python package that emulates maximum functions from MATLAB’s control system toolbox and implements techniques for analyzing any control system object.

4.1 Flowchart of the Simulation Program

4.2 Programming for Simulating Uncertain Model

For simulating the uncertain model in Python, following steps have been taken for developing the program:

  1. 1.

    A constant variation is applied to every uncertain parameter. As an example, values of all uncertain parameters would vary within \(\pm\) 5% of their nominal value.

  2. 2.

    As stated in point 1, a function is created to produce an array consisting five different values of each uncertain parameter within that range. By implementing multiprocessing, the number of values in those arrays can be increased.

  3. 3.

    A for loop is built to run the simulation program described in the above flowchart using single values from those arrays in each iteration.

  4. 4.

    Outside the for loop two null arrays, one for MSE and another for settling time is created. For each iteration, MSE and settling time are added to those arrays, respectively.

  5. 5.

    During each iteration, plots of control signal or frequency response are plotted as per requirement.

  6. 6.

    Average MSE and average settling time for that constant variation are calculated.

  7. 7.

    At last, a small code snippet is created for evaluating stability of the system for those values of uncertain parameters. The flowchart in Fig. 8 describes the same.

    Fig. 8
    figure 8

    Flowchart of program for evaluating stability of the system

    Full size image

5 Stability Analysis of the Overall Closed Loop System

Stability of an LTI system can be defined by calculating the eigenvalues of the “state matrix” of that system. For any bounded initial condition and zero input, an LTI system is called “Lyapunov stable” if the state remains bounded. For any bounded initial condition and zero input, an LTI system is called “Asymptotically stable” if the state converges to zero.

For evaluating stability of the single-link manipulator model, nominal values of the system parameters are listed in Table 2.

Table 2 Nominal values of parameters
Full size table

Substituting these values in the state-space model (7),

$$ \frac{d}{dt}\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \\ {i_{m} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ { - 14.7} & { - 3.4884} & {97.674} \\ 0 & { - 16.279} & { - 20} \\ \end{array} } \right).\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} \theta \\ {\dot{\theta }} \\ \end{array} } \\ {i_{m} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ 2 \\ \end{array} } \right).V $$

Here, state matrix \(A = \left( {\begin{array}{*{20}c} 0 & 1 & 0 \\ { - 14.7} & { - 3.4884} & {97.674} \\ 0 & { - 16.279} & { - 20} \\ \end{array} } \right)\).

Calculated eigenvalues of A are:

\(\lambda_{1} = - 11.6562 + 39.1731i, \lambda_{2} = - 11.6562 - 39.1731i \) and

$$ \lambda_{3} = - 0.176006 $$

So,

  1. 1.

    Two eigenvalues \(\lambda_{1}\) and \(\lambda_{2}\) are complex conjugates, and \(\lambda_{3}\) is a negative real number.

  2. 2.

    \(Re\left( {\lambda_{1} } \right) = Re\left( {\lambda_{2} } \right) < 0\) and \(Re\left( {\lambda_{3} } \right) < 0\).

The negative real part of the eigenvalues implies the asymptotic stability of the overall closed-loop system.

6 Simulation Results

6.1 Plot of Closed-Loop Step Response of the System (Without Any Controller)

In open-loop condition, the arm rotates without stopping, and the angular position of the arm increases as long as the electrical energy is provided, as it can be seen from the Fig. 9. Due to arm’s weight, the curve is slightly bent (Fig. 9).

Fig. 9
figure 9

Open-loop step response of the system

Full size image

6.2 Plot of PID Controlled Step Response of the Nominal System

In case of choosing PID gains, “Manual tuning” has been taken into account. Such a case study with the values of PID parameters is used for simulating; MSE and settling time are presented in Table 3.

Table 3 Values of PID parameters, MSE and settling time for nominal system
Full size table
Fig. 10
figure 10

PID controlled step response of the system

Full size image

Figure 10 shows how perfectly the implemented PID controller fixes the angular position of the arm according to the set point.

6.3 Plot of Squared Error with Time of the Controlled Response

Figure 11 shows how the squared error of the PID controlled system (i.e., SP-PV) is made zero with time.

Fig. 11
figure 11

Squared error versus time plot

Full size image

6.4 Plot of Angular Velocity with Time

In Fig. 12, the change of angular velocity while PID controller is fixing the desired angular position is shown. At around 1.7 to 1.8 s, the angular velocity goes slightly negative and then settles to 0 as angular position is fixed.

Fig. 12
figure 12

Angular velocity versus time plot

Full size image

6.5 Frequency Response of the Uncertain Model

For simulation, two different values for Δ are taken:

Different case studies for these values of uncertainties are shown in Tables 4 and 5 for considering different values of Δ. Figure 13 depicts the frequency response of the uncertain system.

Table 4 Values of PID parameters, MSE and Settling time for uncertainty, Δ = ± 5%
Full size table
Table 5 Values of PID parameters, MSE and Settling time for uncertainty, Δ = ± 7%
Full size table
Fig. 13
figure 13

Bode plot of the uncertain model (Δ = \(\pm\) 5%, Kp = 100, Ki = 50 and Kd = 1)

Full size image

For Δ =  \(\pm\) 5%

For Δ =  \(\pm\) 7%

From the obtained results, it can be said that parameter uncertainty within \(\pm\) 7% of their value is permeable for the model, the model remains stable, and the angular position reference command is tracked within allowable range of mean square error.

7 Conclusion

In this paper, PID controller is designed and implemented to control the angular position of a single-link manipulator system which is a very popular robotic application. The manipulator system has been modeled considering additive uncertainty which makes the system closer to practical system. Simulation experimentation is performed for different values of uncertain parameters. Mean square error is calculated as performance metric along with settling time. As the closed-loop system stability is a major concern, the calculated eigenvalues containing negative real part assures the same for this present work. Application of control system toolbox in Jupyter notebook is another important feature of this work. This work can be further easily extended to embed the simulated controller on a Linux-based system for standalone application.