Keywords

1 Introduction

The relevance of the semiconductor crystal growth using the floating zone technique is motivating the researchers for the past few decades. Steered by the recent developments in the area of micro and nano technologies, thermo-capillary convection (TC) in liquid bridges (LB) has achieved increased attention. The generation of surface tension gradients due to the temperature gradients at the liquid-liquid interface results in a surface flow called as TC from high-temperature region to the low-temperature region [1]. It is well established that beyond a particular Marangoni number (\(Ma_{\text{cr}}\)) corresponding to the applied temperature difference (\(\Delta T_{\text{cr}}\)), the convection undergoes a transition to a time-dependent and 3D state which is commonly referred to as oscillatory TC. This onset of super criticality in the liquid zones is distinguished by the spatiotemporal convective structures such as standing or traveling waves. Experiments conducted under microgravity conditions demonstrated that this spatiotemporal elements of the convective flow can be analyzed in detail in the framework of hydrothermal wave (HTW) instability [2]. The toroidal convection roll inside the LB is reported to be disturbed and displaced circumferentially along the free surface like a sinusoidal wave.

2 Problem Description and Numerical Methodology

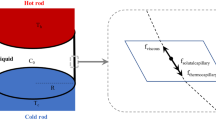
A LB consisting of a high \(Pr\) liquid (\(Pr\) = 39.3) of 5 cSt silicone oil suspended in between two cylindrical rods which are heated differentially is considered for the present investigation as illustrated in Fig. 1.

Fig. 1
figure 1

Configuration of half floating zone (HFZ)

Full size image

The dimensions of the present LB geometry and the properties of the working liquid are taken from the published experimental results of [3]. The modeling and the analysis of the computed oscillatory flow regimes of the present LB problem are performed with the help of a commercially available CFD package ANSYS Fluent 18.1 which is based on finite volume method (FVM). The pressure-velocity coupling is handled using semi-implicit method for pressure-linked equations (SIMPLE) scheme. The dynamics of the LB problem is characterized by thermal convection equations given by continuity, Navier–Stokes, and energy equations as mentioned below.

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {ru_{r} } \right) + \frac{1}{r}\frac{\partial }{\partial \varphi }\left( {u_{\varphi } } \right) + \frac{\partial }{\partial z}\left( {u_{z} } \right) = 0$$
(1)
$$\frac{{\partial u_{r} }}{\partial t} + u_{r} \frac{{\partial u_{r} }}{\partial r} + \frac{1}{r}u_{\varphi } \frac{{\partial u_{r} }}{\partial \varphi } + u_{z} \frac{{\partial u_{r} }}{\partial z} = - \frac{1}{\rho }\frac{\partial P}{\partial r} + \upsilon \left( {\nabla^{2} u_{r} - \frac{{u_{r} }}{{r^{2} }} - \frac{2}{{r^{2} }}\frac{{\partial u_{\varphi } }}{\partial \varphi }} \right)$$
(2)
$$\frac{{\partial u_{\varphi } }}{\partial t} + u_{r} \frac{{\partial u_{\varphi } }}{\partial r} + \frac{1}{r}u_{\varphi } \frac{{\partial u_{\varphi } }}{\partial \varphi } + u_{z} \frac{{\partial u_{\varphi } }}{\partial z} = - \frac{1}{\rho r}\frac{\partial P}{\partial \varphi } + \upsilon \left( {\nabla^{2} u_{\varphi } - \frac{{u_{\varphi } }}{{r^{2} }} + \frac{2}{{r^{2} }}\frac{{\partial u_{r} }}{\partial \varphi }} \right)$$
(3)
$$\frac{{\partial u_{z} }}{\partial t} + u_{r} \frac{{\partial u_{z} }}{\partial r} + \frac{1}{r}u_{\varphi } \frac{{\partial u_{z} }}{\partial \varphi } + u_{z} \frac{{\partial u_{z} }}{\partial z} = - \frac{1}{\rho }\frac{\partial P}{\partial z} + \upsilon \nabla^{2} u_{z} \quad$$
(4)
$$\frac{\partial T}{\partial t} + u_{r} \frac{\partial T}{\partial r} + \frac{1}{r}u_{\varphi } \frac{\partial T}{\partial \varphi } + u_{z} \frac{\partial T}{\partial z} = \alpha \nabla^{2} T\quad$$
(5)

The hot and cold ends of the rods in contact with the working liquid have no-slip, impermeable, and isothermal boundary conditions. Meanwhile, tangential shear stress balance [4] and the heat flux balance at the free surface of the LB are represented as shown below.

$$\begin{aligned} & 2\mu \frac{{{\text{d}}R}}{{{\text{d}}z}}\left( {\frac{{\partial u_{r} }}{\partial r} - \frac{{\partial u_{z} }}{\partial z}} \right) + \mu \left[ {1 - \left( {\frac{{{\text{d}}R}}{{{\text{d}}z}}} \right)^{2} } \right]\left( {\frac{{\partial u_{z} }}{\partial r} + \frac{{\partial u_{r} }}{\partial z}} \right) \\ & = \sigma_{T} \left[ {1 + \left( {\frac{{{\text{d}}R}}{{{\text{d}}z}}} \right)^{2} } \right]^{1/2} \left( {\frac{{{\text{d}}R}}{{{\text{d}}z}}\frac{\partial T}{\partial r} + \frac{\partial T}{\partial z}} \right) \\ \end{aligned}$$
(6)
$$- k\left( {\frac{\partial T}{\partial r} - \frac{{{\text{d}}R}}{{{\text{d}}z}}\frac{\partial T}{\partial z}} \right) = h\left( {T_{{}} - T_{\text{amb}} } \right)$$
(7)

A non-uniform grid mesh which is well refined near the free surface and the solid walls is adopted to resolve the velocity and thermal boundary layers. Grid and time independence study is performed by computing the value of \(\Delta T_{\text{cr}}\) and the corresponding amplitude of liquid temperature fluctuations. Eventually, a grid of size 60 \(\times\) 140 \(\times\) 60) and a time step of dt = 0.0025 are selected as the optimum one. Figure 2 shows the grid mesh employed for the present numerical investigation.

Fig. 2
figure 2

3D grid mesh near the free surface of LB

Full size image

3 Results and Discussion

The critical values deciding the onset of instability \(\Delta T_{cr}\) and \(Ma_{cr}\) have been numerically validated with the experimental results of [3] and were found to be 50 K and 27136, respectively, which is corresponding to a specific ambient temperature of 300 K. The emerging spatiotemporal flow structures observed in the present case are due to the occurrence of a pulsating or standing waveform.

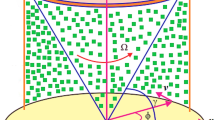
The pulsation of the disturbances is observed to form at particular azimuthal locations of the LB free surface. The critical azimuthal wave number of the present spatiotemporal mode of convection is found to be m = 2 such that 2 m number of thermal spots can be noticed along the free surface and along the generic sections perpendicular to z-axis [5] as shown in Fig. 3. The instantaneous disturbance temperature field shows that the disturbances are pulsating at fixed azimuthal positions instead of rotating. The hot and cold thermal spots are observed to grow or shrink in the axial direction of the LB. The intensity of thermal spots is also found to change with respect to time.

Fig. 3
figure 3

Disturbance temperature field in the cross section at z = 0.5 at different time intervals a t = τ b t = τ/4 c t = τ/2 d t = 3τ/4

Full size image

The azimuthal convective cells in the generic section orthogonal to the z-axis show a periodic variation of their direction of rotation which is a characteristic of the SW, i.e., a particular convective cell which is oriented in the clockwise direction in the first half period of oscillation will change to the anti-clockwise direction in the second half period as presented in Fig. 4. The variation in the oscillatory flow structure at various instants of time is more apparent from the above-shown distribution of the streamlines.

Fig. 4
figure 4

Disturbance flow field in the cross section at a location z = 0.5 at different time intervals a t = τ b t = τ/4 c t = τ/2 d t = 3τ/4

Full size image

The hydrothermal mechanism for the onset of instability can get initiated due to the random occurrence of a hot or cold temperature disturbance on the free surface of the LB. Generation of a hot disturbance results in a thermo-capillary flow in the azimuthal direction, thereby creating two counter-propagating hydrothermal waves away from the disturbance. A radial flow from the cold bulk to the free surface occurs to satisfy the continuity which consequently causes the initial hot disturbance to get cooled. Thus, the disturbances convect along the free surface and replace each other and finally resulting in a pulsating structure as shown in the instantaneous velocity and temperature fields. Moreover, the observed transition to the supercritical state is due to the HTW instability due to the intercoupling between the velocity and temperature fields. It is reported to be Hopf bifurcation which is responsible for the consequent dynamic evolution of the system. The peculiarity of this pulsating mode m = 2 is the divisibility of the oscillatory convective flow structure into four regions about a plane of symmetry. The free surface flows from hot rod to the cold rod created due to the surface temperature gradients, and the corresponding return flow of the bulk fluid inside the liquid zone can be clearly understood from Fig. 5a.

Fig. 5
figure 5

a Flow and temperature fields and b disturbance flow and temperature fields in the meridional plane of the liquid bridge

Full size image

As the present class of critical mode is observed to be the symmetric mode (m = 2), the flow and temperature fields in the meridional section of the LB show a mirror symmetry with respect to the z-axis as shown. Figure 5b illustrates the corresponding disturbance temperature and velocity fields in the same section which is also found to be symmetric about the axis of the LB. The presence of two hot thermal spots on the free surface results in two HTW to generate in the azimuthal direction, each gets split into two counter-propagating partial HTWs. The distribution of the disturbance velocity field shows that the crests of the generated HTWs are oriented in the axial direction of the LB as presented in Fig. 6. A close observation of the orientation of the core region of the azimuthal convective cells in the generic cross section at different axial positions reveals that the generated waveform is an oblique HTW. Hence, these waves exhibit an angle of propagation with respect to the direction of basic free surface flow, having two distinct components along both the directions.

Fig. 6
figure 6

Disturbance flow fields in the cross section at different axial locations

Full size image

The critical azimuthal wave number decides the extension of thermal spots appearing along the azimuthal direction. Generally, the azimuthal extension of temperature spots can be calculated as (360/2 m) [5]. Hence, for m = 2, eight temperature probes are supposed to be necessary to analyze the spatiotemporal flow structure in the liquid. Stabilized liquid temperature fluctuations show that the phase shift between any of the observed temperature fluctuations located in azimuthal direction measure the values 0 and 180 only which is a characteristic of the pulsating behavior as shown in Fig. 7. Furthermore, the amplitudes of the fluctuations are also found to be changing with respect to the spatial locations unlike that of a TW.

Fig. 7
figure 7

Temperature monitor measured at a point on the free surface

Full size image

The analysis of the oscillation frequency of liquid temperature fluctuations on the free surface is carried out using fast Fourier transform (FFT) and presented in Fig. 8. The frequency and amplitude of liquid temperature oscillations in the present case are observed to be 1.6 Hz and 0.21 K, respectively.

Fig. 8
figure 8

Fourier spectrum for liquid temperature oscillations

Full size image

4 Conclusions

A numerical investigation of spatiotemporal flow structures of oscillatory thermo-capillary convection in LBs of a high \(Pr\) liquid is carried out under microgravity conditions. The spatiotemporal mode of convection in the present case is observed to be a pulsating pattern which changes the flow and thermal fields in the liquid zone periodically. The critical azimuthal wave number is found out be equal to 2 which causes four thermal spots to generate on the free surface and on the generic section orthogonal to the z-axis. The dynamic evolution of the flow system has been studied with the help of an analysis of the amplitude and phase shift between the liquid temperature fluctuations.