Keywords

15.1 Introduction

Nowadays, electric vehicles and autonomous photovoltaic systems are widely spread share and their usage increasing with the development of energy storage systems. Safe and durable batteries are the fundamental part of this sort of systems, for this reason battery management system (BMS) is widely used [1].

SOC is defined as the remains power in the battery, due to this reason a strong necessity growth for developing strategies and techniques to accurately estimate the SOC. Therefore, methods are divided in three mains families. The first category consists of the Coulomb counting method [2], which is the well know approach as ampere-hour (Ah). It is based on the integration of the discharge or charge current.

The second categories are based on artificial intelligence, such as artificial neural network (ANN) and fuzzy logic [3]. The rest of methods are generally closed loop techniques such as Kalman filters [3, 4] and sliding mode observers [5, 6] or based on the chemical of the battery such as spectroscopy and the open circuit voltage method (OCV) [7]. Therefore, these two strategies; Kalman filters and the sliding mode observers have high accuracy and their option of performing better under unknown conditions is proved. This paper presents a comparison study of checking performance of the EKF and SMO, an ECM based on first order Thevenin circuit has been established and its parameters determined by using the least square method.

The rest of this paper is organized as follows, in section two an ECM is presented and the process of extracting its parameters is discussed. Follows by the design process of SMO and EKF processes. In section four, the simulation results are elaborated. The manuscript is ended with conclusions and summary.

15.2 Battery Modeling

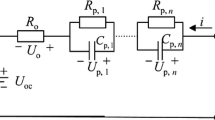
Both EKF and SMO estimators are model-based requires an earlier information of the battery model, the first-order Thevenin model is selected, where the model depicted in Fig. 15.1. It composed of a shunt resistor \({R}_{s}\), an RC parallel branch to characterize the polarization and a nonlinear controlled voltage represent the mapped OCV with SOC.

Fig. 15.1
figure 1

First-order Thevenin battery model

Full size image

In order to map the relationship between OCV and SOC, the OCV-SOC mapping process consists of discharging the battery 10% of its nominal capacity, which reduce the SOC 10%. So, it consists of a pulse current with 10 sequences of a current 1 C-rate and the experiment data stored into a PC host. The final relationship OCV-SOC is presented in Fig. 15.2a. Where the terminal voltage of the battery \({V}_{L}\) captured is depicted in Fig. 15.2b, which shows the battery response under current pulse profile.

Fig. 15.2
figure 2

a The OCV-SOC relationship curve at 25 °C. b Experiment The terminal voltage of the battery

Full size image

The OCV presents the terminal voltage of the battery while no load connected, and the cell achieved the equilibrium steady state after a sequence of pulse current. A magnified view of the terminal voltage under a pulse discharge is presented in Fig. 15.3.

Fig. 15.3
figure 3

A zoomed pulse of the terminal voltage

Full size image

The series resistor presents the internal impedance, which is voltage captured in the moment the load is connected or disconnected. From the drop and jump voltage captured, the series resistor can be computed as follows:

$$R_{{\text{s}}} = {\text{moy}}\left( {\left| {\frac{{U_{1} - U_{2} }}{{I_{L} }}} \right| + \left| {\frac{{U_{3} - U_{4} }}{{I_{L} }}} \right|} \right)$$
(15.1)

where: \({U}_{1}-{U}_{2}\) and \({U}_{3}-{U}_{4}\) represent the drop and jump in tension for each vector respectively, \({I}_{\mathrm{L}}\) is the flows current of the connected load. Therefore, the transient behavior can be exploited to determine the RC branches’ parameters. By applying Matlab curve fitting tool in Fig. 15.3, the terminal voltage and time can present respectively as follows:

$${V}_{t}=U5-{U}_{4}\mathrm{exp}\left(-\frac{t}{T}_{1}\right)$$
(15.2)
$${C}_{1}=\frac{{U}_{4}}{{I}_{L}(1-e\frac{-t0}{{T}_{1}})}$$
(15.3)

where \({t}_{0}\) is the instant time of jumping voltage at voltage (\({U}_{4}\)). The final parameters of the model were identified are given in Table 15.1.

Table 15.1 First order Thevenin model parameters
Full size table

15.3 State of Charge Estimation

15.3.1 Kalman Filters

EKF is considered as an optimal mean to predict and correct time-varying system in a way that minimizes the mean of the squared error. The EKF stat space algorithm is summarized below:

$$\left\{\begin{array}{c}{x}_{k+1}=f\left({x}_{k},{u}_{k}\right)+{w}_{k}\\ {y}_{k}=g\left({x}_{k},{u}_{k}\right)+{v}_{k}\end{array}\right.$$
(15.4)

The terms \({v}_{k}\) and \({w}_{k}\) are random distributions Gaussian representing the error theirs covariances respectively \({Q}_{k}\) and \({R}_{k}\) and the system can be presented as follows:

$${x}_{k}=\{ {V}_{1,k}\,\,\, {SOC}_{k}{\}}^{T}$$
(15.5)
$$\left\{ {\begin{array}{*{20}c} {x_{k + 1} = \left[ {{ }\begin{array}{*{20}c} {e^{{ - \frac{T}{{{\text{T}}_{1} }}}} } \\ 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]x_{k} + \left[ {\begin{array}{*{20}c} {R_{1} \left( {1 - e^{{ - \frac{T}{{T_{1} }}}} } \right)} \\ { - \frac{T}{{C_{n} }}} \\ \end{array} } \right]I_{L,k} + \left[ {\begin{array}{*{20}c} {w_{1,k} } \\ {w_{2,k} } \\ \end{array} } \right]} \\ {y_{{\text{k}}} = \left[ { - 1{ }\frac{\partial OCV}{{\partial SOC}}} \right]x_{{\text{k}}} + \left[ { - {\text{Rs}}} \right] I_{L,k} + v_{k} } \\ \end{array} } \right.$$
(15.6)

where \(T\) is the sampling time, \({T}_{1}={C}_{1}{R}_{1}\) is the polarization time, \({C}_{n}\) is the nominal capacity of the battery.

Step 1: Initialization:

$${\widehat{x}}_{0}^{+}=E\left[{x}_{0}\right]$$
(15.7)
$${P}_{0}= E\left[{(x}_{0}-{x}_{0}^{+}\right){({x}_{0}-{x}_{0}^{+})}^{T}]$$
(15.8)

Step 2: State prediction: and estimation the covariance error matrix:

$${\widehat{x}}_{k+1}^{-}={A}_{k}*{\widehat{x}}_{k}+{B}_{k}*{I}_{L,k}$$
(15.9)
$${P}_{k}^{-}={A}_{k}{P}_{k}{\mathrm{A}}_{\mathrm{k}}^{\mathrm{T}}+{R}_{k}$$
(15.10)

Step 4: Calculating the Kalman coefficient:

$${K}_{k}={P}_{k}^{-}{\mathrm{C}}_{\mathrm{k}}^{\mathrm{T}}{\left[{C}_{k}{P}_{k}^{-}{\mathrm{C}}_{\mathrm{k}}^{\mathrm{T}}+{Q}_{k}\right]}^{-1}$$
(15.11)

Step 5: Update the estimate state and covariance error matrix:

$${\widehat{x}}_{k}={\widehat{x}}_{k+1}^{-}+{K}_{k}({V}_{L,k}-{\widehat{V}}_{t,k})$$
(15.12)
$${P}_{k}=(I-{K}_{k}{C}_{k}){P}_{k}^{-}$$
(15.13)

where \(I\) is an identity matrix, \({\widehat{x}}_{k}\) is the update state estimated from the previous step.

15.3.2 Sliding Mode Observer

The SMO observer has the same structure as the conventional, which is relies on determination of an appropriate feedback switching gain linked with system uncertainty bound. Therefore, the error of the sliding surfaces is defined as:

$$\left\{ {\begin{array}{*{20}l} {e_{VL} = V_{L} - \widehat{V}_{L} } \hfill \\ {e_{z} = z - \hat{z}} \hfill \\ {e_{V1} = V_{1} - \widehat{V}_{1} } \hfill \\ \end{array} } \right.$$
(15.14)

Based on Fig. 15.1, the dynamic state model can be presented by the below equation:

$$\left\{ {\begin{array}{*{20}l} {\dot{V}_{L} = - a_{1} V_{L} + a_{1} V_{ocv} - b_{1} I_{L} } \hfill \\ {\dot{z} = a_{2} V_{L} - a_{2} V_{ocv} + a_{2} V_{1} } \hfill \\ {\dot{V}_{1} = - a_{1} V_{1} + b_{2} I_{L} } \hfill \\ \end{array} } \right.$$
(15.15)

where \({\mathrm{a}}_{1}=1/{\mathrm{R}}_{1}{\mathrm{C}}_{1}\), \({\mathrm{a}}_{2}=1/{\mathrm{R}}_{\mathrm{s}}{\mathrm{C}}_{\mathrm{n}}\), \({\mathrm{b}}_{1}=\frac{{\mathrm{K}}_{1}}{{\mathrm{C}}_{\mathrm{n}}}+\frac{{\mathrm{R}}_{\mathrm{s}}}{{\mathrm{R}}_{1}{\mathrm{C}}_{1}}+\frac{1}{{\mathrm{C}}_{1}}\) and \({\mathrm{b}}_{2}=1/{\mathrm{C}}_{1}\). And the modified SMO can be presented as:

$$\left\{ {\begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {\dot{V}_{L} } \\ {\dot{\hat{z}}} \\ {\dot{V}_{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - a_{1} } & {a_{1} K_{1} } & 0 \\ {a_{2} } & { - a_{2} K_{1} } & {a_{2} } \\ 0 & 0 & { - a_{1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{L} } \\ z \\ {V_{1} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} { - b_{1} } \\ 0 \\ {b_{2} } \\ \end{array} } \right]u + \left[ {\begin{array}{*{20}c} {a_{1} K_{2} } \\ { - a_{2} K_{2} } \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {g_{1} sgn\left( {e_{VL} } \right)} \\ {g_{2} sgn\left( {e_{z} } \right)} \\ {g_{3} sgn\left( {e_{V1} } \right)} \\ \end{array} } \right]} \\ {y = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {V_{L} } \\ z \\ {V_{1} } \\ \end{array} } \right]} \\ \end{array} } \right.$$
(15.16)

where \({g}_{1}\), \({g}_{2}\) and \({g}_{3}\) are the switching gains. The error dynamics of the terminal voltage \({e}_{VL}\) is computed by:

$$\left\{ {\begin{array}{*{20}l} {\dot{e}_{VL} = - a_{1} e_{VL} + a_{1} K_{1} e_{z} + a_{1} K_{2} + d_{1} - g_{1} sgn\left( {e_{VL} } \right)} \hfill \\ {\dot{e}_{z} = a_{2} e_{VL} - a_{2} K_{1} e_{z} - a_{2} K_{2} + a_{2} e_{V1 } + d_{2} - g_{2} sgn\left( {e_{z} } \right)} \hfill \\ {\dot{e}_{V1} = - a_{1} e_{V1} + d_{3} - g_{3} sgn\left( {e_{V1} } \right)} \hfill \\ \end{array} } \right.$$
(15.17)

where \({d}_{1}\), \({d}_{2}\) and \({d}_{3}\) represent the error of modeling. Therefore, based on the Lyapunov stability theory, the choosing candidate of Lyapunov function.

$${V}_{r}(e)=0.5{ e}_{VL}^{2}$$
(15.18)

To ensure the existence of the sliding regime, the derivative of the candidate Lyapunov function has to be negative. So, after developing the following \(\dot{{V}_{r}}\), the value of \({g}_{1}\) that guarantee \(\dot{{V}_{r}} < 0\) is \({g}_{1}\gg \left|{d}_{1}\right|\). Since the \({\dot{e}}_{VL}={e}_{VL}=0\).

Thereby, the signum function replaced by the saturation function as depicted in Fig. 15.4, to reduce the chattering phenomenon which has the equation expressed as:

$$sat\left( {e_{VL} } \right) = \left\{ {\begin{array}{*{20}l} {sgn\left( {e_{VL} } \right)} \hfill & {if\;\left| {e_{VL} } \right| > M} \hfill \\ {\frac{{e_{VL} }}{M}} \hfill & {if\;\left| {e_{VL} } \right| < M} \hfill \\ \end{array} } \right.$$
(15.19)
Fig. 15.4
figure 4

The saturation function

Full size image

With \(M\) is the boundary of width.

15.4 Simulation and Results Discussion

In order to investigate the two estimators, the SMO and EKF were tested and simulated under Matlab/Simulink platform for a lithium-ion battery of 10 Ah nominal capacity. The simulation results are depicted in Fig. 15.5a for continuous discharge and followed by error committed by both estimators in Fig. 15.5b for discharge current of 1 C. Then the results of pulse discharge are presented in Fig. 15.6a, the comparison error between them is illustrated in Fig. 15.6b.

Fig. 15.5
figure 5

a SOC estimation using SMO and EKF for 1 C-rate. b SOC estimation error for both observatory algorithms

Full size image
Fig. 15.6
figure 6

a SOC estimation using SMO and EKF for pulse current. b SOC estimation error for both algorithms

Full size image

And the statistics of the simulation are summarized in Table 15.2. From the above simulation results, it is clear that the two methods perform better in SOC estimation, despite that the SMO is marginally more robust than EKF as shown in Table 15.2. The SMO is really robust and deal with uncertainties. Besides, it has high convergence and small time of execution.

Table 15.2 Simulations statistics
Full size table

15.5 Conclusion

Estimating the SOC with high efficiency is the key factor for managing the batteries and guarantee of its long-life cycle and avoids a harmful usage. This paper selects a simple ECM and mapped OCV-SOC relationship. Therefore, a comparative study of SMO and EKF observers.

The designed estimators were investigated in term of robustness and accuracy in accordance with the battery and figure out the time execution of each estimator technique. It can be concluded that both strategies are competitive in term of precision but the SMO is more robust against uncertainties and modeling errors, converges rapidly, and easy to implement.