Keywords

1 Review of the Theoretical Background

1.1 Bearing Capacity of Shallow Foundations

The ultimate bearing capacity and failure of a shallow foundation has been defined in a variety of ways. Defining ultimate bearing capacity with a critical state seems the most reasonable; however, this state is not often achieved as many soils will continue to increase capacity while loading (strain hardening), or when the soil strength/foundation size is large enough such that the critical state cannot be reached. In this case, a criterion for peak strength must be set. In this work, ultimate bearing capacity will be defined by either a peak strength, or the asymptote of a fitted hyperbolic curve as proposed by Kondner [1].

Terzaghi [2] proposed the original ultimate bearing capacity for plane-strain failure of a strip (continuous) footing. This equation has been subsequently modified by researchers to account for other factors including embedment depth and variation in footing shape, or to modify the original bearing capacity factors [3,4,5,6,7]. Vesić [6] proposed Eq. (1) for the calculation of ultimate bearing capacity:

$$q_{ult} = c^{\prime}N_{c} s_{c} d_{c} + \sigma^{\prime}_{zD} N_{q} s_{q} d_{q} + 0.5\gamma^{\prime}BN_{\gamma } s_{\gamma } d_{\gamma }$$
(1)

where \(c'\) is effective cohesion, \(\sigma_{zD}^{'}\) is the effective stress at the depth of embedment, \(\gamma '\) is the effective soil unit weight, B is the footing width, Nc, Nq, and \(N_{\gamma }\) are bearing capacity factors, Sc, Nq, and \(s_{\gamma }\) are shape factors, and dc, dq, and \(d_{\gamma }\) are depth factors. The bearing capacity, shape, and depth, factors used in this work may be found in any standard textbook on the topic. The shape factors are those proposed by Hansen [4] whereas Nc and Nq are the original bearing capacity factors from Prandtl [8].

1.2 Suction, Stress, and Strength in Unsaturated Soils

Soil water characteristic curves (also known as soil water retention curves) describe the relationship between suction and water content in soils [9] and other porous media [10, 11]. Several models have been proposed to fit discrete laboratory data and to continuously describe the soil water characteristic curve [12,13,14]. Van Genuchten [13] proposed Eq. (2) as a model for the soil water characteristic curve (SWCC):

$$S_{e} = \frac{{\theta - \theta_{r} }}{{\theta_{s} - \theta_{r} }} = \left[ {\frac{1}{{1 + \left( {\alpha \psi } \right)^{n} }}} \right]^{{1 - \frac{1}{n}}}$$
(2)

where Se is effective saturation, \(\theta\) is the volumetric water content (i.e., \(V_{w} /V_{t}\)), \(\theta_{s}\) is the saturated water content (numerically equal to the porosity), \(\psi\) is matric suction (i.e., \(\psi = u_{a} - u_{w}\)), and \(\theta_{r}\) is the residual water content, and \(\alpha\), m and n are fitting parameters; however, both \(\alpha\) and \(n\) do have physical correlations. Soils above the groundwater table are partially saturated, where nonlinearity in stress arises due to the existence of both a gas and liquid phase in the pores. Bishop [15] proposed an effective stress parameter \(\chi\) which is a function of suction and physical soil properties, into Terzaghi’s effective stress equation:

$$\sigma^{\prime} = \sigma - u_{a} + \chi \left( {u_{a} - u_{w} } \right)$$
(3)

\(\chi = 1\) at saturation and \(\chi = 0\) when dry. The last term in Eq. (3) is the suction stress, \(\sigma_{s}\) [9, 16]:

$$\sigma_{s} = \chi \left( {u_{a} - u_{w} } \right)$$
(4)

where \(\chi\) is often approximated as equal to effective saturation, Se. Using Bishop’s definition of effective stress, the Mohr-Coulomb failure criterion can be modified such that it includes the effects of matric suction and partial saturation:

$$\tau_{f} = c^{\prime} + \left( {\sigma - u_{a} } \right)\tan \phi^{\prime} + \chi \psi \tan \phi^{\prime}$$
(5)

where, \(\tau_{f}\) is the shear stress at failure.

To account for the effects of partial saturation on soil response in situ, it is necessary to know the matric suction profile. Using the Gardner [17] conductivity function, Lu and Griffiths [18] derive an equation to calculate matric suction as a function of permeability, infiltration/evaporation rates, and height above the groundwater table:

$$\psi = - \frac{1}{\alpha }\ln \left[ {\left( {1 + \frac{q}{{k_{s} }}} \right)e^{{ - \alpha \gamma_{w} z}} - \frac{q}{{k_{s} }}} \right]$$
(6)

where q is the flux rate (evaporation is positive and infiltration negative), ks is the saturated hydraulic conductivity, z is the distance above the ground water table, and \(\alpha\) is the fitting parameter used in the van Genuchten equation (assumed to be the inverse of the air-entry suction). When there is no net flow, the equation reduces to the hydrostatic case, \(\psi = \gamma_{w} z\).

1.3 Shallow Foundations Emplaced in Unsaturated Soils

More recently, researchers have studied the effects of partial saturation and suction stress in foundation performance through foundation load tests in partially saturated soils [19,20,21,22,23,24] and by continued modification of the conventional bearing capacity equation [25,26,27]. These studies have shown that partially saturated soils, especially silts and clays, often have bearing capacities greater than the predicted bearing capacity for a completely dry or completely saturated soil. To account for partial saturation, the cohesion term is typically modified within the bearing capacity equation to account for apparent cohesion caused by suction stresses [25, 27, 28].

2 Theoretical Development and Numerical Example

In traditional foundation design, resistance is derived from three primary components: cohesion, unit weight, and surcharge loads. These three components are directly influenced by the value of the friction angle through bearing capacity factors. The shape of the failure surface is understood to be a function of friction angle [8]. Here we assume that the shape of the failure surface does not change as a function of varying suction stresses and soil unit weights. We further assume that the mean apparent cohesion (\(\overline{{c^{\prime\prime}}}\)) defined in Eq. (7) can be directly implemented into the bearing capacity equation:

$$\overline{{c^{\prime\prime}}} = \frac{1}{\ell }\int\limits_{\ell } {c^{\prime\prime}ds} = \frac{1}{\ell }\int\limits_{\ell } {\sigma_{s} \tan \phi^{\prime}ds} = \frac{1}{\ell }\int\limits_{\ell } {\psi \chi \tan \phi^{\prime}ds}$$
(7)

where \(\ell\) is the length of the failure surface. This is appropriate since failure in the shallow foundation bearing capacity framework is defined by the Mohr-Coulomb (M-C) failure criterion and apparent cohesion due to suction stress shifts the failure envelope upward in M-C space. The general bearing capacity equation is thus modified as shown in Eq. (8):

$$q_{ult} = (c^{\prime} + \overline{{c^{\prime\prime}}} )N_{c} s_{c} d_{c} + q_{s} N_{q} s_{q} d_{q} + 0.5\overline{{\gamma^{\prime}}} BN_{\gamma } s_{\gamma } d$$
(8)

where \(c'\) is the soil effective cohesion,, \(q_{s}\) is the overburden stress at the base of the footing (including the suction stress), and \(\overline{{\gamma^{\prime}}}\) is the average effective soil unit weight within the log spiral failure surface. The modified overburden and effective unit weight terms in Eq. (8) are defined in Eqs. (9) and (10), respectively:

$$q_{s} = \left\{ \begin{aligned} \sigma_{zD} + \sigma_{s,D} = \sigma_{zD} + \left( {\psi \chi } \right)_{D} \,if\,D < z_{w} \hfill \\ \sigma_{zD} - u\,if\,D \ge z_{w} \hfill \\ \end{aligned} \right.$$
(9)
$$\overline{{\gamma^{\prime}}} = \frac{1}{A}\int\limits_{A} {\gamma^{\prime}\left( \psi \right)dA}$$
(10)

where \(\sigma_{zD}\) is the net normal vertical stress at the depth of embedment, \(\sigma_{s,D}\) is the suction stress at the depth of embedment, zw is the depth of the groundwater table, u is porewater pressure, \(A\) is the total area contained by the failure surface.

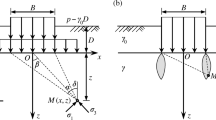
To demonstrate how this approach is implemented, an example strip footing embedded in partially saturated soil is considered. The following example includes soil with hydraulic properties selected such that the majority of suction stresses exist within 3 m of the groundwater table \(\left( {\left\{ {\theta_{s} ,\,\theta_{r} ,\,\alpha ,\,n} \right\} = \left\{ {0.385, \,0.0385, \,0.175 \,{\text{kPa}}^{ - 1} ,\,2.5} \right\}} \right)\); shear strength (\(\phi^{\prime} = 20^\circ\)) was selected such that the failure surface extends to a depth of nearly 3 m (for a 2 m wide footing embedded 0.5 m). The failure surface extends to just above the groundwater table, as shown in Fig. 1. In this example, the failure surface extends to a depth of 2.85 m. This foundation is considered loaded to the ultimate limit state, where continuous plastic flow occurs.

Fig. 1
figure 1

Contours of degree of saturation in the soil profile for the numerical example. The groundwater table is at the base of the figure and total profile height is 3 m. Only one side of the failure surface is shown for clarity

Full size image

The saturation profile of the soil can be defined by the proximity of the layer to the depth of the groundwater table. For hydrostatic conditions in a homogenous soil, matric suction increases linearly above the groundwater table; this results in nonlinear variation of water content, Bishop’s \(\chi\), and suction stress (Eq. 4). Using this approach, the saturation of the soil can be determined at any point along the failure surface. This enables the calculation of average suction stress acting along the failure surface. Figure 2 shows the saturation and corresponding apparent cohesion \(c^{\prime\prime} = \sigma_{s} \tan \phi '\), across the failure surface according to its proximity from the groundwater table.

Fig. 2
figure 2

Failure surface of the shallow foundation colored by the saturation profile. Lines of demarcation indicate apparent cohesion at that location

Full size image

The averaged unit weight in the failure wedge is used directly in the modified framework. The moist unit weight profile is calculated with Eq. (11):

$$\gamma_{m} = \left( {G_{s} \left( {1 - \theta_{s} } \right) + \theta_{s} S_{e} } \right)\gamma_{w}$$
(11)

where \(\gamma_{m}\) is the moist unit weight, \(G_{s}\) is the specific gravity, \(\gamma_{w}\) is the unit weight of water, and all other terms are as previously defined. From Eq. (11), the average unit weight is \(\overline{\gamma '} = 17.3 \,{\text{kN}}/{\text{m}}^{3}\). The conventional approach assumes that the average unit weight varies between the buoyant unit weight when the groundwater table is above the depth of embedment and a dry/moist unit weight when the groundwater table is greater than the depth of embedment plus the footing width (D + B). For this particular soil, the unit weight using the conventional approach is estimated to be 16.4 kN/m3, a difference of 0.9 kN/m3.

The third term in Vesić’s bearing capacity equation is overburden—the effective stress at the base of the footing. In unsaturated soils, this effective stress will include the effects of suction stress. Overburden is the simplest consideration in the Vesić equation, requiring only knowledge of the soil unit weight above the footing and the suction stress at the embedment depth. In this example, the suction stress at the depth of embedment is 2.7 kPa. The net normal (total) stress can be calculated as the integral of the soil unit weight from the surface to the depth of embedment as shown in Eq. (12):

$$q_{s} = \left( {\psi \chi } \right)_{zD} + \mathop \smallint \limits_{0}^{D} \gamma \left( z \right)dz = \sigma_{s} + \sigma_{t}$$
(12)

where all terms are previously defined. The calculated surcharge in this example is qs = 11.1 kPa. The conventional approach would use the estimated soil unit weight of 16.4 kN/m3, as calculated previously, multiplied by the depth of embedment (0.5 m), resulting in an 8.2 kPa overburden.

Combining these considerations, the modified inputs can be used with the Vesić equation. The bearing capacity is calculated to be 187 kPa. If the unmodified approach was used, the bearing capacity would be calculated as 144 kPa. Thus, the modified approach predicts a 30% increase in bearing capacity relative to the conventional approach.

3 Comparison to Measured Results

In this section, we compare the measured responses of shallow foundation load tests from the literature and the calculated bearing capacity from the modified approach considering the effects of partial saturation. This section is important in assessing the ability of the proposed approach to reasonably predict bearing capacity for shallow foundations in partially saturated soils.

There are many works in the literature concerning the bearing capacity of shallow foundation, but there are very few that include soil water characteristic curve (SWCC) and permeability data. This information is crucial for implementation in this work, thus the SWCC must be either predicted or provided. The grain size distribution and soil classification can be used to predict unsaturated soil properties using, e.g., pedotransfer functions. In this work, if the SWCC is not provided, it is estimated in one of two ways: (1) using the values presented by Carsel and Parrish [29] based on USDA soil classifications; or (2) by use of an unsaturated soil database/pedotransfer application, SoilVision (Fredlund 2011), if the grain size distribution curve is provided. Carsel and Parrish [30] collected unsaturated properties for over 15,000 soil samples and calculated mean values of van Genuchten [13] parameters according to the USDA textural classification. Average values were reported for each classification, organizing \(\alpha\), \(n\), \(\theta_{s}\), \(\theta_{r}\), and \(k_{s}\) based on percent clays, silts, and sands. The SoilVision software (Fredlund [30]) can be used to categorize unsaturated soil based on soil type and grain size distribution either by pedotransfer functions or by comparison to an existing soil database. Through this process, unsaturated parameters can be predicted for implementation in this work.

Another requirement for the literature used in this comparative study is that either an ultimate bearing capacity was achieved in the load test or the ultimate bearing capacity can be calculated from the load displacement curve. If the ultimate state was not achieved, the Kondner [1] hyperbolic equation was fitted to the load displacement curve and \(q_{ult}\) taken as the hyperbolic asymptote. Table 1 lists the seven sources used for comparison. The modified bearing capacity was compared to the measured bearing capacity from the load tests presented in these works. Results from Vanapalli and Mohamed [25] and Vanapalli and Mohamed [23] are presented in Figs. 3, 4, and  5 to compare the bearing capacity equation proposed by Vanapalli and Mohamed and the modified approach proposed in this work. In these figures, matric suction is plotted against bearing capacity.

Table 1 Literature van Genuchten [13] parameters used in the comparative study
Full size table
Fig. 3
figure 3

Bearing capacity versus variation in average matric suction for a 100 × 100 mm plate loaded on the surface

Full size image
Fig. 4
figure 4

Bearing capacity versus variation in average matric suction for a 150 × 150 mm plate loaded on the surface

Full size image
Fig. 5
figure 5

Bearing capacity versus variation in average matric suction for a 150 × 150 mm plate embedded 150 mm

Full size image

The predicted bearing capacity calculated using the modified approach proposed herein and the measured bearing capacities from Vanapalli and Mohamed [23, 25] show close agreement. For all three load tests, the bearing capacity predicted in this work quickly reduces after suctions of 5–6 kPa to the conventional bearing capacity equation. This is quite different to the work of Vanapalli and Mohamed [23, 25], who predict a more gradual decline in bearing capacity with increasing suction. The solution proposed by Vanapalli and Mohamed does not decrease to the conventional bearing capacity equation.

The soil used for the tests presented in Figs. 4, 5, and 6 has an air-entry suction around 4–5 kPa and a high van Genuchten n fitting parameter (i.e., relatively uniform pore size), so saturation decreases quickly as the matric suction is increased beyond the air-entry suction. The results from the proposed approach capture this rapid desaturation (and corresponding decrease in suction stress) in an organic way—it simply follows the trend dictated by the SWCC and the suction stress profile. The proposed method also shows better agreement with the conventional bearing capacity for dry (high matric suction) and saturated soils (zero matric suction) where suction stress should be very close to zero. The proposed approach does not require any assumption of fitting parameters, but is completely dependent on the soil water characteristic curve. In Fig. 5, Vanapalli and Mohamed [23] suggest that a friction angle of ϕ′ = 35.3° be used for embedded foundations, while 39° (1.1ϕ′) be used for surface foundations to account for dilation. This work shows that friction angles of 39° and 35.3° bracket the measured bearing capacity. This may imply that dilation cannot be ignored for embedded foundations, but rather, that dilation is merely partially suppressed, which is consistent with conventional shear strength theory.

Fig. 6
figure 6

Measured bearing capacity versus predicted bearing capacity for database of load tests

Full size image

Figure 6 presents a comparison between the measured bearing capacity and the predicted bearing capacity using the proposed and conventional approaches for the load tests listed in Table 1. Lines were fit to the data for comparison against the 1:1 line. The line fit to the modified approach shows closer agreement to the 1:1 line than the conventional approach. The conventional bearing capacity equation will generally underpredict bearing capacity. The slope of the best-fit line for the modified approach is 0.93 while the slope for the conventional approach is 0.43. Using linear regression against the 1:1 line gives a coefficient of determination of R2 = 0.806 (versus 0.811 for the best-fit line). Figure 6 shows that the modified approach gives close agreement with measured data, implying that it is potentially a viable approach for calculating shallow foundation bearing capacity in unsaturated soils.

4 Summary and Conclusions

The purpose of this work was to develop a theoretical framework for calculating ultimate bearing capacity for shallow foundations in partially saturated soils. We have proposed a modification to the conventional Vesić shallow foundation bearing capacity equation to incorporate recent literature on unsaturated soil mechanics. Implementation of concepts from unsaturated soil mechanics included the consideration of apparent cohesion and soil unit weight as they vary with suction and water content, respectively, and the inclusion of suction stress on in calculating overburden stress.

The proposed modifications have been evaluated relative to load tests reported in the literature for shallow foundations in partially saturated soils. The modified bearing capacity equation shows closer agreement with measured bearing capacities than the conventional bearing capacity equation. This implies that the proposed theoretical model for bearing capacity is worthy of additional directed study for use in shallow foundation design. Based on the load tests considered, the conventional method underpredicts bearing capacities in unsaturated soils.