Keywords

1 Introduction

Reliability and risk data analysis are especially important when the risks are high. Accordingly, modern approach aims to give protection when the risks are felt to be high via probability based analysis [1, 2]. Probabilistic design techniques are being used in a wide spectrum of application areas in industry including aerospace, automotive, mechanical, civil, chemical, electrical, and manufacturing industries.[1,2,3].

In general, the reliability of a product is directly related to many factors like the type of manufacturing process, environment, external load, cost etc. which must be considered in design [4, 5]. Today during especially vehicle development process, engineering based effort is spent [6, 7]. Probabilistic design, on the other hand, provides an alternative approach to these studies.

Naturally there are many uncertainties which have to be considered in design. Hence, it is necessary to use safety factors in a deterministic design. However, in probabilistic design, statistical methods are used [7,8,9].

Being a design parameter, the fatigue phenomenon is a slow process, so it introduces numerous uncertainties [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37]. Therefore, as it is explained, in addition to the numerical and experimental analysis, a probabilistic analysis is also necessary to treat the problem completely.

For spot welded structures fatigue analysis is done using different fatigue life prediction models—the nominal stress, the notch stress, the notch strain, the fracture mechanics, and volumetric fatigue approaches etc. Since most of the existing numerical analyses are still limited [38], reliability analysis is also necessary for reliable failure predictions. Hence in this study, in addition to experimental study, a reliability analysis was also done.

2 Materials and Methods

2.1 Comparison of Probabilistic and Deterministic Design Methodologies

Deterministic approaches to the engineering problems may result in inconsistent products especially in the future because of the limitations in design, service, material, manufacturing etc. [38, 39]. On the other hand, there is no single method available for solving all engineering problems efficiently. As a result, many probabilistic design methods have been created for solving engineering problems [3, 39, 40].

In deterministic design it is necessary to use Factor of Safety (FS) to consider afore mentioned uncertainties. Selection of factor of safety generally depends upon the engineer’s knowledge or experience [3, 39, 40].

In the probabilistic design, on the other hand, the performance function which originated from the limit state theory is expressed mathematically as [39]

$$g\left( x \right) = R - P$$
(1)

where R and P represent resistance and load, respectively; x is the vector of basic random variables, \(g\left( x \right) < 0\) and \(g\left( x \right) > 0\) are the failure region and the safe region, respectively. The Probability of Failure (POF) can be evaluated via Eq. (2) [3]

$${\text{POF}}\, = \,\int\limits_{g\left( x \right)\,\langle \,0} {...\int {f_{x} \left( x \right)dx} }$$
(2)

If the limit state function combines more than two statistically independent variables, \(x_{i}\) the variance of response \(g\left( {x_{i} } \right)\) can be approximated by Taylor expansion with eliminating higher order terms. In this case, the variance for a function, \(\sigma_{g}\), can be expressed analytically via Eq. (3), where \(\sigma\) and \(\mu\) are the variable standard deviation and its mean, respectively [39]

$$\sigma_{g}^{2} \approx \,\sum {\left( {\frac{\delta g}{{\delta x_{i} }}} \right)}^{2} \sigma_{{x_{i} }}^{2}$$
(3)

The standard normal variant—which is known as First Order Reliability Method (FORM)—and then The Probability of Failure (POF) can be calculated by Eqs. (4), and (5), respectively [39]

$$z = \, - \frac{{\mu_{R} - \mu_{P} }}{{\sigma_{g} }}$$
(4)
$${\text{POF}} = \,\phi \left( z \right)$$
(5)

In the standard normal variant method, the limit state is linearized around the “design point”. Accordingly, The POF is given by Eq. (6) [39]

$${\text{POF}} = \,\varphi \left( { - \beta } \right)$$
(6)

2.2 A Probabilistic Study on Fatigue Strength of Spot Weld Joints

Reliability of a machine component is very important. Because depending on the reliability, a component will be unsafe under certain circumstances. Hence reliability linked to probability can be defined as the probability that failure will not occur [7,8,9].

The probabilistic fatigue analysis used here is based on the work of Pan [4] and Ertas [3]. In this type of analysis, the variability of the material yield strengths, which are DQSK and HSLA steels, is taken into account via using nearly normal distribution. In many cases, because the loading exhibits sinusoidal behavior it is necessary to use plus or minus tolerance, \(L\), and the standard deviation, \(\sigma\), shown in Eqs. (7) and (8), respectively [10, 41] which are valid for all normal distribution:

$$L = 3\sigma$$
(7)
$$\sigma = L/3$$
(8)

There are many mathematics of random variables for different mathematical expressions which can be found in text books [10, 41]. Table 1, for instance, shows the fundamental formulas. In this table, “X” and “Y” represent independent random variables, on the other hand, “Z” and “\(a\)” represent the result and any constant, respectively.

Table 1 Fundamental formulas
Full size table

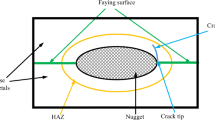
Case 1: Fatigue Life Analysis: In this case, simply an attempt is made to solve the problem using conventional solution technique. For a typical spot welded Modified Tensile Shear (MTS) specimen shown in Fig. 1, the calculation was done.

Fig. 1
figure 1

A typical geometry of the two spot-welded modified tensile shear (MTS) type specimen (top and side views)

Full size image

Conventionally fatigue life of a spot welded plate can be calculated using the following formula which is called as “Morrow’s mean stress equation”.

$$\frac{\Delta \varepsilon }{2} = \varepsilon_{a} = \frac{{\Delta \varepsilon_{e} }}{2} + \frac{{\Delta \varepsilon_{p} }}{2} = \frac{{\sigma^{\prime}_{f} - \sigma_{m} }}{E}\left( {2N_{f} } \right)^{b} + \varepsilon^{\prime}_{f} \left( {2N_{f} } \right)^{c}$$
(9)

where \(\Delta \varepsilon\), \(\sigma_{m}\), \(N_{f}\), \(c\), \(E\), \(\sigma_{f}^{{\prime}}\), \(\varepsilon_{f}^{{\prime}}\), \(b\), \(\Delta \varepsilon_{e}\), \(\Delta \varepsilon_{p}\) represent local strain at the notch, mean stress, cyclic life of the specimen, material constant determined experimentally, modulus of elasticity, the fatigue strength coefficient, the fatigue ductility coefficient, material constant determined experimentally, alternating true elastic strain and alternating true plastic strain, respectively.

In this case shown in Fig. 1 let’s assume that the spot welds have to carry 9700 lb. In addition, the spot weld diameters, actually the heat affected zone (HAZ) diameters, change between 0.926–0.928 in. for the outer diameter and 0.850–0.852 in. for the inner diameter. Here it is known that spot welds consist of two different parts which are spot weld oneself (the center of spot weld) and heat affected zone (HAZ). Because the deformation occurs inside of the HAZ, it is necessary to examine HAZ instead of spot weld itself. So we choose the diameters according to HAZ and because of welding mechanism it was chosen the diameters with tolerance values.

Under this loading case, a tensile stress occurs and this stress value can be calculated using Eq. (10):

$$S\, = \,\frac{P}{{\left( {{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}} \right)\left( {D^{2} - d^{2} } \right)}}$$
(10)

where \(D\), \(d\), \(S\), \(P\) represent mean outside diameter (inches, random variable), mean inside diameter (inches, random variable), unit stress (psi), and applied force (lb).

Using aforementioned data, unit stress is calculated and found as 91,396 psi. Assuming tensile yield strength as 130,000 psi and ultimate tensile strength as 135,000 psi, the safety factors can be calculated by using Eq. (11):

$$S\, = \,\frac{9700}{{\left( {{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}} \right)(Z)}}\, = \,\frac{12350,\!4}{Z}$$
(11)

where \(Z = \left( {D^{2} - d^{2} } \right)\) is a random variable. In this application, the outer diameter and inner diameters are 0.927 \(\pm\) 0.001 inches and 0.851 \(\pm\) 0.001 inches, respectively. Standard deviation is taken as tolerance/3. Random variables of outer and inner diameters are:

$$D = \left( {\mu_{D} , \sigma_{D} } \right){ } = { }\left( {0.927,{ }0.00033} \right){\text{ in}}{.}$$
$$D = \left( {\mu_{d} , \sigma_{d} } \right){ } = { }\left( {0.851,{ }0.00033} \right){\text{ in}}{.}$$

The mean value and standard deviation of \(Z\) can be found easily and summarized as the following,

$$Z = \left( {\mu_{Z} , \sigma_{Z} } \right) = { }\left( {0.13513,{ }0.000831} \right){\text{ in}}{.}^{2}$$

Hence, stress value became;

$$S = { }\left( {12350.4/{\text{Z}}} \right){ } = { }\left( {12350.4/\left( {0.13513,{ }0.000831} \right)} \right)$$
(12)

Likewise, the mean value and standard deviation can be found as follows;

$$\mu_{S} { } = { }\left( {12350.4/\mu_{Z} } \right){ } = { }91396{\text{ psi}}$$
$$\sigma_{S} = \left( {12350.4} \right)\frac{{\sigma_{Z} }}{{\mu_{Z}^{2} }} = 562 {\text{ psi}}$$
$$S = \left( {\mu_{S} , \sigma_{S} } \right) = { }\left( {91396,{ }562} \right){\text{ psi}}$$

If difference distribution, \(W = T - S\), is taken into account, the following values are obtained. Here:

$$T = {\text{ tensile yield strength }} = \left( {\mu_{T} , \sigma_{T} } \right) = { }\left( {130000,{ }7500} \right){\text{ psi}},{ }$$
$$S{ } = {\text{ calculated stress }} = { }\left( {\mu_{S} , \sigma_{S} } \right)$$
$$\mu_{W} = { }130000 - 91396{ } = { }38604{\text{ psi and}}$$
$$\sigma_{W} = \sqrt {7500^{2} + 562^{2} } = 7521{\text{ psi}}$$

Hence difference distribution become;

$$W = \left( {\mu_{W} , \sigma_{W} } \right) = { }\left( {38604,{ }7521} \right)$$

In order to apply W to standard distribution, N = (0, 1), the following formula can be used:

$$X = \frac{{0 - \mu_{W} }}{{\sigma_{W} }}{ } = { }\left( {\left( {0 - 38,604} \right) - 7521} \right){ } = { } - 5.133$$

where 0 and \(X\) represent the horizontal coordinate in the difference distribution and corresponding coordinate in the standard distribution table, respectively.

Using a suitably expanded table of standard normal distribution, it can be found that the area to the right of this \(X\) coordinate is equal to 0.9999 or probability of failure equal to 0.0001. The corresponding reliability of 0.9999 can be designated by the shorthand expression as:

$$R = { }0.9999$$

Here using the given function (tensile stress formula, that is Eq. (10)) and NESSUS the probability of failure and corresponding reliability are seen the same as found by hand calculation.

Secondly let’s look at the effect of variable load, which results in fatigue failure in components. Hence, the loading, that is the mean value, and the corresponding standard deviation will be as follows:

$$P = \left( {9700, 9700*10\% of 9700} \right) = { }\left( {9700,{ }970} \right){\text{ lbs}},$$

Hence tensile stress equation (our “G” function) became;

$$S = \frac{{\left( {\frac{4}{\pi }} \right)P}}{Z}$$
(13)

where

$$Z = D^{2} - d^{2} = \left( {0.13513,{ }0.000831} \right){\text{ in}}^{2}$$

Using Table 1,

$$\left( {\frac{4}{\pi }} \right)P = \left( {12350.4,{ }1235} \right){\text{ lb and}}$$
$$S = { }\left( {\left( {12350.4,{ }1235} \right)/\left( {0.13513,{ }0.000831} \right)} \right){ } = { }\left( {91396,{ }9159} \right){\text{ psi}}$$

For this new situation:

$$T = \left( {130000,{ }7500} \right),{\text{ given}}$$
$$\mu_{W} = 130000 - 91396{ } = { }38604{\text{ psi}},{\text{ unchanged}}$$
$$\sigma_{W} = \sqrt {7500^{2} + 9159^{2} } = 11838{\text{ psi}},{\text{ changed:}}{\text{ so}}$$
$$W = \left( {\mu_{W} , \sigma_{W} } \right) = \left( {38,604,{ }11,838} \right){\text{ psi}},$$

Finally to apply \(W\) to standard normal distribution, \(N = (0,1)\), it can be used the following formula,

$$X = \frac{{0 - \mu_{W} }}{{\sigma_{W} }}{ } = { }\left( {\left( {0 - 38,604} \right)/11,838} \right){ } = { } - 3.26$$

Using a suitably expanded table of standard normal distribution, it can be found that the area to the right of this \(X\) coordinate to be equal to 0.99944 or probability of failure equal to 0.00056. The corresponding reliability of 0.99944 can be designated by the shorthand expression as:

$$R{ } = { }0.99944$$

Here using the given function (tensile stress formula, that is Eq. (10)) and NESSUS the probability of failure and corresponding reliability are seen the same as found by hand calculation.

This steps can be expanded and used for calculation of the probability of failure for fatigue life, that is for the load applications of \(N_{f}\), using Eq. (9). For this case the reliability function is defined as [42]:

$$L_{N} \left( n \right)\, = \,P\left( {N\rangle \,n} \right)$$
(14)

and the probability of failure in the interval (from first to the nth application of load) [1, n] is [42]:

$$F_{N} \left( n \right)\, = \,1 - L_{N} \left( n \right)\, = \,P\left( {N \le n} \right)$$
(15)

Finally let’s look at the fatigue behavior of spot welded TS specimen overall considering Eq. (9). There are some constants and material properties. The so called values for a material (DQSK or DIN 1623 steel material) and loading case (cycling between 3700 and 200 N) using previous studies, [20, 21], can be summarized as the following:

$$\sigma_{m} = \left( {\mu_{{\sigma_{m} }} ,\sigma_{{\sigma_{m} }} } \right) = \left( {159.7,{ }22.933} \right){\text{ MPa}}$$

\(N_{f}\) = for life it was wanted 1,000,000 (infinite life) with an anticipated normal distribution over the fatigue life of the spot welded TS specimen such that its standard deviation is 10% of its mean value, then the mean value and standard deviation, that is the case, for \(N_{f}\) will be:

$$N_{f} = \left( {\mu_{{N_{f} }} ,\sigma_{{N_{f} }} } \right) = { }\left( {1000000,{ }100000} \right),$$
$$c = { } - 0.4,$$
$$E = 207000{\text{ MPa}},$$
$$\sigma_{f}^{^{\prime}} = { }499{\text{ MPa}},$$
$$\varepsilon_{f}^{^{\prime}} = { }0.104,$$
$$b = { } - 0.06,$$
$$\varepsilon_{a} = \left( {\mu_{{\varepsilon_{a} }} ,\sigma_{{\varepsilon_{a} }} } \right) = { }\left( {0.000684,{ }0.00075} \right),$$

Using Eq. (9) with the aforementioned values, the value of the function becomes;

$$G\, = \,\frac{{\sigma^{\prime}_{f} - \sigma_{m} }}{E}\left( {2N_{f} } \right)^{b} + \varepsilon^{\prime}_{f} \left( {2N_{f} } \right)^{c} - \varepsilon_{a}$$
$$G\, = \,\frac{{499 - \sigma_{m} }}{207,000}\left( {2N_{f} } \right)^{ - 0.06} + 0.104\left( {2N_{f} } \right)^{ - 0.4} - \varepsilon_{a}$$
(16)

where

$$N_{f} = \left( {\mu_{{N_{f} }} ,\sigma_{{N_{f} }} } \right) = { }\left( {1,500,000,{ }150,000} \right),$$
$$\sigma_{m} = \left( {\mu_{{\sigma_{m} }} ,\sigma_{{\sigma_{m} }} } \right) = { }\left( {159.7,{ }22.933} \right),{\text{ and}}$$
$$\varepsilon_{a} = \left( {\mu_{{\varepsilon_{a} }} ,\sigma_{{\varepsilon_{a} }} } \right) = { }\left( {0.000684,{ }0.00075} \right).$$

It is clear that the probability of failure or the corresponding reliability of the spot welded MTS specimen obtained by using the last formula (Eq. (16)) will be much lower than the computed values, since the resulting mean value and standard deviation is taken into account along with each component with their mean values and standard deviations. Here it was considered only one component of the loading and in this single load two cases, which are the tensile load itself and diameter of the HAZ, was examined as an example. In short, using the “G” function, that is Eq. (16) with NESSUS, it is found that the probability of failure is 0.337, which is an expected value.

Case 2: Correlations among applied load and experimental fatigue life data: In fatigue analysis, the uncertainty is originated from two main subjects. The first one is physical properties based uncertainties and the second one is modeling uncertainty which is related to analysis assumptions for models used. In order to figure out whether the stress versus fatigue life (S–N) curve of fatigue tests have a considerable scatter, the Coefficient of Variation (COV) of fatigue life (N) can be checked. Typically fatigue life data used to define fatigue strength of welded joint is characterized by a COV equals to 0.50 [43]. In this study, the experimental fatigue life data for every loading case have lower COV values as seen in Table 2 [14] which shows the reliability of the data, in other words the uncertainty of the experimental fatigue life data have a considerable scatter.

Table 2 The reliability data for MTS type spot welded specimens [14]
Full size table

In addition to checking COV value, it can also be looked at the regression coefficients values via the regression analysis, or scatter diagram, of the experimental data. Table 3 shows the coefficient of determination (\(R^{2}\)) values of the regression analysis or the scatter diagrams of MTS type spot weld data.

Table 3 Regression analysis (scatter diagram) results for MTS type spot welded specimens
Full size table

The result of the regression analysis (scatter diagram), which is the estimated coefficient of determination, given in Table 3 indicate that the predictability of the regression is quite high and the general applicability of the experimental fatigue life data are good.

Secondly, to find a distribution from observed (experimental) data, as an example for selected loading case (3700–200 N), and then whether the assumed distribution is acceptable for a significance level (α), i.e. for α = 1%, Kolmogorov–Smirnov (K-S) statistical test was used. Before doing K-S test, the plots, experimental fatigue life data versus Cumulative Distribution Function (CDF) and Probability Density Function (PDF) values were obtained using a commercial software, NESSUS (Southwest Research Institute) [44], and shown in Fig. 2.

Fig. 2
figure 2

CDF and PDF values for experimental fatigue life data of MTS type spot welded specimen under 3700–200 N loading case

Full size image

The maximum difference between CDFs of the ordered data can be estimated using Eq. (17) [45]:

$$D_{n} \, = \,\max \,\left| {F_{X} \left( {x_{i} } \right) - S_{n} \left( {x_{i} } \right)} \right|$$
(17)

\(F_{X} \left( {x_{i} } \right)\) and \(S_{n} \left( {x_{i} } \right)\) can be estimated via Eq. (18) [45]:

$$F_{X} (x_{i} )\, = \,\Phi \left[ {\frac{{\ln \,x_{i} \, - \lambda }}{\xi }} \right]$$
(18)

where \(\lambda\) and ξ are the two parameters of the lognormal distribution.

$$S_{n} \left( {x_{i} } \right)\, = \,\left\{ \begin{gathered} 0,\,\,\,\,\,x\,\langle \,x_{1} \hfill \\ \frac{m}{n},\,\,\,x_{m} \, \le \,x\, \le \,x_{m + 1} \hfill \\ 1,\,\,\,\,\,\,x\, \ge \,x_{n} \hfill \\ \end{gathered} \right\}$$
(19)

The CDF of \(D_{n}^{\alpha }\) can be related to the significance level α as [45];

$$P\left( {D_{n} \, \le \,D_{n}^{\alpha } } \right)\, = \,1 - \alpha$$
(20)

and \(D_{n}^{\alpha }\) values at various significance levels α can be obtained from a standard mathematical table as shown in reference [45]. Table 4 shows the K-S test results of the experimental fatigue life data for MTS type spot welded specimen taking into account the loading case of 3700–200 N.

Table 4 K-S test results for experimental results of MTS type spot welded specimens under the loading of 3700–200 N
Full size table

Using 1% significance level \(D_{n}^{\alpha } = D_{5}^{0.01}\) can be obtained from a standard mathematical table [45], which is K-S test, as 0.669. Because all the \(D_{n}\) values founded are less than from \(D_{n}^{\alpha } = D_{5}^{0.01} =\) 0.669, the assumed lognormal distribution is acceptable for 1% significance level and K-S test and this shows the reliability of the data.

3 Conclusions

In this work, the fatigue failure behavior of MTS specimens was investigated probabilistically and the following points were determined:

The anticipated failure probability, for the function of Eq. (11), of “one in ten million” indicates a very safe design; this is the case in spite of the comparatively low safety factor of 1.42, based on the mean values of yield strength and stress.

The stress-strength reliability value of 0.9994 (for the function of Eq. (13)) corresponds to 6 failures per 10,000. This is a relatively lower reliability than that obtained in first case (from Eq. (11)) for the constant load condition, and would be considered unacceptable in most applications.

For the final case (for the function of Eq. (16)), the reliability of the spot welded MTS specimen under fluctuating loading condition, that is in terms of fatigue loading, is low because the system was considered overall and it is clear that failure will occur. This value also shows why fatigue loading is one of the most important deformation mechanisms.