Mathematical Modeling for an Optimal Order Inventory with Demand Dependent Selling Price, Nonlinear Stock, and Nonlinear Holding Cost

Abstract

In the present paper an EOQ model has been developed with nonlinear holding cost, where demand is found to be linearly dependent on selling price and nonlinearly on inventory level. In this model the prevailing assumption of zero ending inventory level has been changed into a nonzero ending inventory level. Here an inventory model with shortages is analyzed which is partially backlogged. The main purpose of the inventory model is to find out the optimal order quantity along with ending inventory level so as to maximize retailer’s total profit per unit time and also to determine the best-selling price of a given product. The trade credit policy is also introduced in the model. To demonstrate our model a numerical example has been presented and a sensitivity analysis is incorporated to highlight the findings of the suggested inventory model.

1 Introduction

From past few years, a lot of attention has been paid towards the inventory management policy. Price is an important factor on which the demand of a product depends. A common question is what should be the selling price of a product? Although the ability to vary price in an inventory cycle is appreciable but sometimes the retailer may choose to keep constant price for administrative convenience. A system of inventory for non-instantaneous deteriorating items with price-dependent demand was formulated. According to many researchers, it has been observed that a display of large quantities of a product increases the product demand within the customers. Demand is also found to be dependent on the stock in hand. An inventory production model in an imperfect production process where demand rate is dependent on both selling price as well as time was developed by Sarkar et al. [7]. A deteriorating item inventory model was formulated by Hsieh and Dye [4] considering the displayed stock level and sales price-dependent demand. Leopoldo Eduardo Cárdenas—Barrón et al. [8] formulated an EOQ inventory model considering nonlinear demand dependent on stock level, nonlinear stock dependent holding cost, and trade credit. In this paper, an inventory model has been proposed taking shortages into consideration. This paper demonstrates an inventory model where demand is nonlinear with nonlinear holding cost along with trade credit policy. Demand is considered to be a function of the amount of stock in hand and price, when the stock is nonzero, whereas demand is considered constant during the backlog period. A nonzero ending inventory level instead of zero ending inventory level has been developed. Backlogging gives an idea about the quantity of product to be ordered. Backlogging is useful for the retailer to have an idea of the order quantity on one side but it also comes with loss of sales due to shortage on the other side. In this paper we are calculating the optimal selling price, order quantity as well as the ending inventory level.

This paper is sorted out as follows. Section 2 states the assumptions and describes the notations which are necessary to depict the proposed inventory model. Section 3 builds up the inventory model considering nonlinear demand, nonlinear holding cost, along with trade credit policy. Section 4 presents theoretical results and optimization methods for optimizing the total profit. Section 5 solves few numerical examples. Section 6 depicts sensitivity analysis as well as discusses few observations. At the end, Sect. 7 provides future research directions and few conclusions.

2 Notation and Assumptions

The following notations and assumptions have been used as described below.

2.1 Assumptions

Demand is considered to be the function of price and stock level, given by

$$\begin{array}{*{20}l} {{\text{D}}({\text{t}}) = \alpha \left( {a - bp} \right)\left[ {q(t)} \right]^{ \beta } } \hfill & {{\text{when}}\;q(t) > 0} \hfill \\ {\quad \quad\,\,= \alpha } \hfill & {{\text{when}}\;q(t) \le 0 } \hfill \\ \end{array}$$

It is deterministic in nature and a > 0, b > 0.

• 1. Holding cost of the inventory is considered to be a nonlinear function of stock level formulated as

  $$H(t) = c_{h} \left[ {q\left( t \right)} \right]^{\gamma } \quad {\text{where}}\;\gamma > 0$$

  With the decline of stock level, it is found that holding cost also decreases. For $\gamma =1$ we obtain an inventory model where holding cost is linearly dependent on stock.

• 2. Instantaneous replenishment rate, with negligible lead time.

• 3. Inventory system planning horizon is considered to be infinite.

• 4. In this case we have considered a single-level policy of trade credit where the retailer/manufacturer/supplier grants a credit policy to his or her customers for a given slot of time with well-defined terms and conditions.

• 5. Shortages are permitted in this model, and it is partially backlogged with backlogging parameter δ.

2.2 Notation

Notation	Description
Parameters
c o	Replenishment price per order
c	Cost of purchasing per unit
c h	Holding cost per unit per unit time
c b	Shortage cost per unit per unit time
c l	Cost of lost sale per unit
γ	Holding cost elasticity; γ > 0
	Elasticity of demand; 0 ≤ β < 1
δ	Partial backlogging parameter;
	Fraction of the demand within the
	Stock out period which is backlogged,
	ϵ [0,1]
α	Demand rate scale parameter
t 1	Time at which inventory level position
	Reaches to zero
T	Length of the replenishment cycle
M	Trade credit period granted by the
	Supplier to the retailer
I e	Interest percentage per unit time
	Gained by the retailer
I p	Interest percentage per unit time paid
	By the retailer
Functions
q(t)	Inventory level at a given time t where
	0 ≤ t ≤ T
TP (Q, B, p)	Total profit per unit time
Decision Variables
Q	Lot size per cycle
B	Ending inventory level at time T
p	Selling price per unit

3 Mathematical Modeling of the Inventory Model with Nonlinear Stock Dependent Holding Cost and Nonlinear Demand with Trade Credit

Inventory model having a nonzero ending level of inventory has been developed where holding cost is found to have a nonlinear dependence on stock, demand is a function of selling price and nonlinear stock level. Initially in the beginning of the inventory cycle Q units of a product exist. A replenishment order is placed when the level of inventory reaches to B units, then an order quantity of Q − B units is placed which brings back the stock level again to the height of Q units at the beginning of the next cycle. The supplier grants a trade credit period M to his or her retailer additionally. For the inventory model with shortage (B ≤ 0), the total profit per unit time has been derived.

3.1 An Inventory Model with Shortage

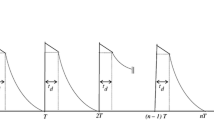
Initially Q units of an item are purchased by the retailer. After that the lot size of Q units decreases due to demand during the interval [0, T]. At t = t₁ the level of inventory reaches to zero. After that shortages occur and it is partially backlogged at the rate δ, the inventory level drops further down than zero. The inventory situation can be best explained by the following differential equations:

$$\frac{dq\left( t \right)}{{dt}} = - \alpha \left( {a - bp} \right)\left[ {q\left( t \right)} \right]^{\beta } ,\quad 0 < t \le t_{1}$$

(1)

$$\frac{dq\left( t \right)}{{dt}} = - \alpha \delta ,\quad t_{1} < t \le T$$

(2)

With the following boundary conditions: q(T) = B ≤ 0, q(0) = Q.

Solving the differential Eqs. (1) and (2) we get

$$q(t) = [Q^{1 - \beta } - \alpha \left( {a - bp} \right)\left( {1 - \beta } \right)t]^{{\frac{1}{1 - \beta }}} \quad 0 < t \le t_{1}$$

(3)

$$q(t) = B + \alpha \delta \left( {T - t} \right)\quad t_{1} < t \le T$$

(4)

Using the condition q(t₁) = 0 in Eq. (4) we get

$${t}_{1}=T+\frac{B}{\alpha \delta }$$

(5)

Using the continuity conditions from Eqs. (4) and (3) at the point t = t₁, the cycle time is determined as follows:

$$T=\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }$$

(6)

Different costs associated with this inventory model with shortage are as follows:

• 1. Ordering cost of the item per order

  $$= C_{0}$$

  (7)

• 2. Inventory holding cost per cycle $({\text{C}}_{{{\text{hol}}}} ) = c_{h} \int_{0}^{{t_{1} }} {\left[ {q(t)} \right]^{\gamma } dt}$

  $$\begin{aligned} C_{{{\text{hol}}}} = & \int\limits_{0}^{{t_{1} }} {[Q^{1 - \beta } - \alpha \left( {a - bp} \right)\left( {1 - \beta } \right)t]^{{\frac{\gamma }{1 - \beta }}} dt} \\ C_{{{\text{hol}}}} = & \frac{{c_{h} }}{{\alpha \left( {a - bp} \right)\left( {\gamma + 1 - \beta } \right)}}\\&\left\lceil {Q^{\gamma + 1 - \beta } - \left\{ {Q^{1 - \beta } - \alpha \left( {a - bp} \right)\left( {1 - \beta } \right)t_{1} } \right\}^{{\frac{\gamma + 1 - \beta }{{1 - \beta }}}} } \right\rceil \\ \end{aligned}$$

  (8)

  Substituting the value of t₁ from Eq. (5) into the above expression we get.

  $${\text{C}}_{{{\text{hol}}}} = \frac{{c_{h} }}{{\alpha \left( {a - bp} \right)\left( {\gamma + 1 - \beta } \right)}}Q^{\gamma + 1 - \beta }$$

  (9)

• 3. Cost of purchasing

  $$= c(Q - B)$$

  (10)

• 4. Revenue collected from sales during the given period (SR)

  $$= p(Q - B)$$

  (11)

• 5. Shortage cost (C_sho) during the inventory cycle $= c_{b} \int_{{t_{1} }}^{T} {\left[ { - q(t)} \right]dt}$

  $$\begin{aligned} C_{sho} = & - c_{b } \int\limits_{{t_{1} }}^{T} {\left[ {B + \alpha \delta \left( {T - t} \right)} \right]dt} \\ = & - c_{b} \left[ {B\left( {T - t_{1} } \right) + \frac{\alpha \delta }{2}(T - t_{1} )^{2} } \right] \\ \end{aligned}$$

  (12)

  Putting the value of t₁ and T in the above expression shortage cost reduces to

  $${\text{C}}_{{{\text{sho}}}} = \frac{{c_{b} B^{2} }}{2\alpha \delta }$$

  (13)

• 6. The opportunity cost (OC_ls) due to loss of sales during the inventory cycle

  $$\begin{aligned} & = c_{l } \int\limits_{{t_{1} }}^{T} {\alpha \left( {1 - \delta } \right)dt} \\ & = c_{l } \alpha \left( {1 - \delta } \right)(T - t_{1} ) \\ \end{aligned}$$

  Substituting the value of t₁ and T from Eqs. (5) and (6) into the above expression, the cost of opportunity further simplifies to

  $${\text{OC}}_{{{\text{ls}}}} = - \frac{{c_{l} \left( {1 - \delta } \right)B}}{\delta }$$

  (14)

In accordance with the policy of granting trade credit, the manufacturer/supplier offers a specific time period (M) to his/her retailer. Depending on the trade credit period the following cases occur:

CASE-1: $0 < M \le t_{1}$

CASE-2: $t_{1} < M \le T$

CASE-3: M > T

Case-1:

Trade credit period is less than or equal to the time period when the inventory level reaches to zero.

Here the supplier provides a trade credit period to his or her retailer but it is less than or equal to t₁. It is to be observed that at the end of credit time M, the retailer faces interest charges and he or she must pay the interest during the time interval [M, T]. Therefore, the interest paid is determined as follows:

$${\text{IP}} = cI_{p} \left[ {\frac{{[Q^{1 - \beta } - \alpha \left( {a - bp} \right)\left( {1 - \beta } \right)M]^{{\frac{2 - \beta }{{1 - \beta }}}} }}{{\alpha \left( {a - bp} \right)\left( {2 - \beta } \right)}}} \right]$$

(15)

Since the retailer has a credit time period M, the retailer earns interest up to time t = M. Therefore, the interest earned (IE) is calculated as shown below:

$$\begin{aligned} {\text{IE}} = & pI_{e} \int\limits_{0}^{M} {\int\limits_{0}^{t} {\alpha \left( {a - bp} \right)\left[ {q\left( u \right)} \right]^{\beta } dudt} + pI_{e} \int\limits_{0}^{M} {\left[ { - B} \right]dt} } \\ = & pI_{e} \left[ {\left( {Q - B} \right)M + \frac{{[Q^{1 - \beta } - \alpha \left( {a - bp} \right)\left( {1 - \beta } \right)M]^{{\frac{2 - \beta }{{1 - \beta }}}} - Q^{2 - \beta } }}{{\alpha \left( {a - bp} \right)\left( {2 - \beta } \right)}}} \right] \\ \end{aligned}$$

(16)

Total profit per unit time, 

$$TP_{1}{(Q,B,p)}=\frac{{X}_{1}}{T}$$

(17)

X₁ = revenue collected from sales + interest earned − interest paid−cost of lost sales − shortage cost − ordering cost − holding cost − cost of purchasing

$$\begin{aligned} X_{1} & = {\text{SR}} + {\text{IE}} - c(Q - B) - c_{o} - {\text{C}}_{{{\text{hol}}}} - {\text{C}}_{{{\text{sho}}}} \\ & \quad - {\text{IP}} - {\text{OC}}_{{{\text{ls}}}} \\ \end{aligned}$$

(18)

Problem 1

$$\begin{aligned} & {\text{Maximize}}\;TP_{1} (Q,B,p) = \frac{{X_{1} }}{T} \\ & {\text{Subject to}}\quad 0 < M \le t_{1} \\ \end{aligned}$$

(19)

Case-2:

Trade credit time is greater than the time at which inventory level reaches to zero but it is less than or equal to the cycle length.

In this case, the trade credit time period M is greater than t₁ but less than or equal to T. Here the retailer does not need to pay interest since the trade credit period M is found to be greater than t₁.

$${\text{IP}} = 0$$

(20)

The retailer does not need to pay interest but earns interest. The interest earned is calculated as shown below:

$$\begin{aligned} {\text{IE}} & = pI_{e} \left[ {\int_{0}^{M} { - Bdt } + \int_{0}^{{t_{1} }} {\int_{0}^{t} {\alpha \left( {a - bp} \right)\left( {q\left( u \right)} \right)^{\beta } dudt} } } \right] \\&\quad+ \int\limits_{0}^{{t_{1} }} {\left( { \alpha \left( {a - bp} \right)\left( {q\left( t \right)} \right)^{\beta } dt} \right)\left[ {M - t_{1} } \right]} \\ & = pI_{e} \left[ { - BM + \left[ {\frac{{Q^{2 - \beta } }}{{\alpha \left( {a - bp} \right)\left( {1 - \beta } \right)\left( {2 - \beta } \right)}}} \right] + Q\left[ {M - \frac{{Q^{1 - \beta } }}{{\alpha \left( {a - bp} \right)\left( {1 - \beta } \right)}}} \right]} \right] \\ \end{aligned}$$

(21)

The total profit per unit time is given by

$$TP_{2} \left( {Q,B,p} \right) = \frac{{X_{2} }}{T}$$

(22)

X₂ = revenue collected from sales + interest earned − cost of lost sales − ordering cost − cost of purchasing − shortage cost − holding cost − interest paid

$$\begin{aligned} X_{2} & = {\text{SR}} + {\text{IE}} - {\text{C}}_{{{\text{hol}}}} - c_{o} - {\text{C}}_{{{\text{sho}}}} - {\text{IP}} - {\text{OC}}_{{{\text{ls}}}} \\ & \quad - c(Q - B) \\ \end{aligned}$$

(23)

Problem 2

$$\begin{aligned} & {\text{Maximize}}\;TP_{2} \left( {Q,B,p} \right) = \frac{{X_{2} }}{T} \\ & {\text{Subject to}}\quad t_{1} < M \le T \\ \end{aligned}$$

(24)

Case-3:

Trade credit time is greater than the cycle time.

Here, the trade credit period M is greater than T. In this case the retailer does not need to pay interest since the trade credit period M is greater than T.

$${\text{IP}} = 0$$

(25)

There is no requirement of paying interest by the retailer but he earns interest in this phase. The interest earned is given by

$$\begin{aligned} &{\text{IE}}\\ & \,\,= pI_{e} \left[ \int\limits_{0}^{M} - Bdt + \int\limits_{0}^{{t_{1} }} \int\limits_{0}^{t} \alpha \left( {a - bp} \right)\left( {q\left( u \right)} \right)^{\beta } dudt\right.\\&\left. \quad+ \int\limits_{0}^{{t_{1} }} {\left( { \alpha \left( {a - bp} \right)\left( {q\left( t \right)} \right)^{\beta } dt} \right)\left[ {M - t_{1} } \right]} \right] \\ &\,\, = pI_{e} \left[ { - BM + \left[ {\frac{{Q^{2 - \beta } }}{{\alpha \left( {a - bp} \right)\left( {1 - \beta } \right)\left( {2 - \beta } \right)}}} \right] + Q\left[ {M - \frac{{Q^{1 - \beta } }}{{\alpha \left( {a - bp} \right)\left( {1 - \beta } \right)}}} \right]} \right] \\ \end{aligned}$$

(26)

Total profit per unit time is given by

$$TP_{3} \left( {Q,B,p} \right) = \frac{{X_{3} }}{T}$$

(27)

X₃ = interest earned + revenue collected from sales − cost of lost sales − ordering cost − cost of purchasing − shortage cost − holding cost − interest paid

$$\begin{aligned} X_{3} & = {\text{SR}} + {\text{IE}} - {\text{C}}_{{{\text{hol}}}} - c_{o} - {\text{C}}_{{{\text{sho}}}} - {\text{IP}} - {\text{OC}}_{{{\text{ls}}}} \\ & \quad - c(Q - B) \\ \end{aligned}$$

(28)

Problem 3

$$\begin{aligned} & {\text{Maximize}}\;TP_{3} \left( {Q,B,p} \right) = \frac{{X_{3} }}{T} \\ & {\text{Subject to}}\quad T < M \\ \end{aligned}$$

(29)

4 Theoretical Results and Optimization Procedures

The total profit functions formulated below are very complex in nature. It is not always easy to find out a closed form solution of the decision variables. Additionally, mathematically sometimes it is hard to present the concavity property of the total profit gained per unit time. So, in order to optimize the total profit earned per unit time, a search algorithm is used.

4.1 An Inventory Model with Shortage

Case-1:

$$\begin{aligned}&{TP}_{1}\left(Q, B, p\right)=\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\right]\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\ &\left.\quad+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.\quad-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]\end{aligned}$$

(30)

Differentiating partially Eq. (30) with respect to Q we get

$$\begin{aligned}{H}_{1}&=\frac{\partial {TP}_{1}(Q, B, p)}{\partial Q}\\&= \left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left\{\left(p-c\right)-\frac{{c}_{h}{Q}^{\gamma -\beta }}{\alpha \left(a-bp\right)}\right.\right.\\&\left.\left.\quad-\frac{c{I}_{p}{Q}^{-\beta }{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{1}{1-\beta }}}{\alpha \left(a-bp\right)}+p{I}_{e}M\right.\right. \\&\left.\left.\quad+\frac{p{I}_{e}\left\{\left\{{Q}^{-\beta }({{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M)}^{\frac{1}{1-\beta }}\right\}-{Q}^{1-\beta }\right\}}{\alpha (a-bp)}\right\}\right]\\&\quad-\frac{{Q}^{-\beta }}{\alpha \left(a-bp\right){\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.\quad-\frac{c{I}_{P}}{\alpha \left(a-bp\right)\left(2-\beta \right)} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]=0\end{aligned}$$

(31)

Next differentiating Eq. (30) partially with respect to B we get

$$\begin{aligned}{H}_{2}&=\frac{\partial {TP}_{1}(Q, B, p)}{\partial B}\\&=\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\right]\left[c-p-\frac{{c}_{b}B}{\alpha \delta }+\frac{{C}_{l}\left(1-\delta \right)}{\delta }-pM{I}_{e}\right]\\&\quad+\frac{1}{\alpha \delta {\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }\right.\\&\left.\quad+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.\quad-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]\end{aligned}$$

(32)

Differentiating Eq. (30) with respect to p we get

$$\begin{aligned}{H}_{3}&=\frac{\partial {TP}_{1}(Q, B, p)}{\partial p}\\&=\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left[Q-B-\frac{bc{I}_{p}M{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}}{a-bp}\right.\right.\\&\left.\left.+p{I}_{e}\left\{\frac{bM{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}}{a-bp}\right.\right.\right.\\&\left.\left.\left.+\frac{b\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right)}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)}\right\}\right.\right.\\&\left.\left.+{I}_{e}\left\{\left(Q-B\right)M+\frac{\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right)}{\alpha \left(a-bp\right)\left(1-\beta \right)}\right\}\right.\right.\\&\left.\left.-\frac{bc{I}_{p}\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}\right)}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)}-\frac{b{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{2}(\gamma +1-\beta )}\right]\right]\\&-\frac{b{Q}^{1-\beta }}{\alpha {\left(a-bp\right)}^{2}(1-\beta ){\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]\end{aligned}$$

(33)

Differentiating Eq. (31) with respect to Q we get

$$\begin{aligned}\frac{\partial {H}_{1}}{\partial Q}&= \frac{-2{Q}^{-\beta }}{\alpha (a-bp)){\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\left[\left(p-c\right)-{c}_{o}-\frac{{c}_{h}{Q}^{\gamma -\beta }}{\alpha \left(a-bp\right)}\right.\\&\left.\,\,+p{I}_{e}\left[M+\frac{\left[{Q}^{-\beta }{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{1}{1-\beta }}-{Q}^{1-\beta }\right]}{\alpha \left(a-bp\right)}\right]\right.\\&\left.-\frac{c{I}_{P}{Q}^{-\beta }}{\alpha (a-bp)} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{1}{1-\beta }}\right]\\&+\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left[-\frac{c{I}_{p}({Q}^{-2\beta }{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{\beta }{1-\beta }}}{a-bp}\right.\right.\\&\left.\left.+\frac{\beta {Q}^{-1-\beta }{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}}{a-bp}\right.\right.\\&\left.\left.+\frac{p{I}_{e}}{\alpha (a-bp)}\left\{-{Q}^{-\beta }\left(1-\beta \right)+{Q}^{-2\beta }{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{\beta }{1-\beta }}\right.\right.\right.\\&\left.\left.\left.-{Q}^{-1-\beta }{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}\right\}-\frac{b{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{2}(\gamma +1-\beta )}\right]\right]\\&+\left[\frac{2{Q}^{-2\beta }}{{\alpha }^{2}{(a-bp)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}+\frac{\beta {Q}^{-1-\beta }}{\alpha (a-bp){\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\,\,\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }} \right]\end{aligned}$$

Differentiating Eq. (32) with respect to B we get

$$\begin{aligned}\frac{\partial {H}_{2}}{\partial B}&= \left[\frac{2}{{\alpha }^{2}{\delta }^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}\right]\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.\quad-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]\\&\quad-\frac{{c}_{b}}{\alpha \delta \left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}+\frac{2}{\alpha \delta {\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\quad\left[c-p-pM{I}_{e}-\frac{B{c}_{b}}{\alpha \delta }+\frac{{Bc}_{l}(1-\delta )}{\delta }\right]\end{aligned}$$

(35)

Differentiating Eq. (33) with respect to p, we get

$$\begin{aligned}\frac{\partial {H}_{3}}{\partial p}&= \frac{2b{Q}^{1-\beta }}{\alpha (1-\beta ){(a-bp)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\quad\left[Q-B-\frac{bc{I}_{p}M{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}}{\alpha \left(a-bp\right)}\right.\\&\left.\quad+p{I}_{e}\left[\frac{bM{{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}}{a-bp}\right.\right.\\&\left.\left.\quad+\frac{b\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right)}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)}\right]\right.\\&\left.\quad+{I}_{e}\left[M\left(Q-B\right)+\frac{\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right)}{\alpha \left(a-bp\right)\left(1-\beta \right)}\right]\right.\\&\left.\quad-\frac{bc{I}_{P}\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{2-\beta }{1-\beta }}\right)}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)}-\frac{b{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{2}(\gamma +1-\beta )}\right]\\&\quad+\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left[-\frac{2{b}^{2}c{I}_{p}M\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}\right)}{{\left(a-bp\right)}^{2}}\right.\right.\\&\left.\left.\quad+p{I}_{e}\left[\frac{2{b}^{2}M\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{1}{1-\beta }}\right)}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)}\right.\right.\right.\\&\left.\left.\left.\quad+\frac{{b}^{2}{M}^{2}\alpha \left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{\beta }{1-\beta }}\right)}{\left(a-bp\right)}\right.\right.\right.\\&\left.\left.\left.\quad+\frac{2{b}^{2}\left({\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta } \right)}{\alpha {\left(a-bp\right)}^{3}\left(2-\beta \right)}\right]\right.\right.\\&\left.\left.\quad+2{I}_{e}\left[\frac{bM\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{\beta }{1-\beta }}\right)}{\left(a-bp\right)}\right.\right.\right.\\&\left.\left.\left.\quad+\frac{b\left({\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta } \right)}{\alpha {\left(a-bp\right)}^{2}\left(2-\beta \right)}\right]\right.\right.\\&\left.\left.\quad-\frac{{b}^{2}{M}^{2}\alpha c{I}_{p}\left({{(Q}^{1-\beta }-\alpha M(a-bp)(1-\beta ))}^{\frac{\beta }{1-\beta }}\right)}{\left(a-bp\right)}\right.\right.\\&\left.\left.\quad-\frac{2{b}^{2}c{I}_{p}\left({\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }} \right)}{\alpha {\left(a-bp\right)}^{3}\left(2-\beta \right)}-\frac{2{b}^{2}{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{3}(\gamma +1-\beta )}\right]\right]\\&\quad-\left[\frac{2{b}^{2}{Q}^{2-2\beta }}{{\alpha }^{2}{\left(a-bp\right)}^{4}{\left(1-\beta \right)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}\right.\\&\left.\quad-\frac{2{b}^{2}{Q}^{1-\beta }}{\alpha {\left(a-bp\right)}^{3}(1-\beta ){\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[\left(Q-B\right)M+\frac{\left[{\left\{{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right\}}^{\frac{2-\beta }{1-\beta }}-{Q}^{2-\beta }\right]}{\alpha \left(a-bp\right)\left(2-\beta \right)}\right]\right.\\&\left.\quad-\frac{c{I}_{P}}{\alpha (a-bp)(2-\beta )} {\left[{Q}^{1-\beta }-\alpha \left(a-bp\right)\left(1-\beta \right)M\right]}^{\frac{2-\beta }{1-\beta }}\right]\end{aligned}$$

(36)

Case-2:

$$\begin{aligned}&{TP}_{2}\left(Q, B, p\right)\\&\quad=\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\right]\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]\end{aligned}$$

(37)

Differentiating partially Eq. (37) with respect to Q we get

$$\begin{aligned}{G}_{1}&=\frac{\partial {TP}_{2}(Q, B, p)}{\partial Q}\\&= \left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left\{\left(p-c\right)-\frac{{c}_{h}{Q}^{\gamma -\beta }}{\alpha \left(a-bp\right)}+p{I}_{e}\left(M-\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)}\right)\right\}\right]\\&\quad-\frac{{Q}^{-\beta }}{\alpha \left(a-bp\right){\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\quad-\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}\right)\right]\right]=0\end{aligned}$$

(38)

Next differentiating Eq. (37) partially with respect to B we get

$$\begin{aligned}{G}_{2}&=\frac{\partial {TP}_{2}(Q, B, p)}{\partial B}\\&= \left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\right]\left[c-p-\frac{{c}_{b}B}{\alpha \delta }+\frac{{C}_{l}\left(1-\delta \right)}{\delta }-pM{I}_{e}\right]\\&\quad+\frac{1}{\alpha \delta {\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }\right.\\&\left.\quad+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]=0\end{aligned}$$

(39)

Differentiating Eq. (37) with respect to p we get

$$\begin{aligned}{G}_{3}&=\frac{\partial {TP}_{2}(Q, B, p)}{\partial p}\\&=\left[\frac{1}{\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }}\left[Q-B-p{I}_{e}\left(\frac{b{Q}^{2-\beta }}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right)(2-\beta )}\right)\right.\right.\\&\left.\left.\quad+{I}_{e}\left\{-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right\}\right.\right.\\&\left.\left.\quad-\frac{b{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{2}(\gamma +1-\beta )}\right]\right]-\frac{b{Q}^{1-\beta }}{\alpha {\left(a-bp\right)}^{2}\left(1-\beta \right){\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}\right)\right]\right]=0\end{aligned}$$

(40)

Differentiating Eq. (38) with respect to Q we get

$$\begin{aligned}\frac{\partial {G}_{1} }{\partial Q}&=\left[\frac{-2{Q}^{-\beta }}{\alpha (a-bp){\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\quad\left[\left(p-c\right)-\frac{{c}_{h}{Q}^{\gamma -\beta }}{\alpha \left(a-bp\right)}+p{I}_{e}\left(M-\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)}\right)\right]\\&\quad+\left[\frac{1}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}\left[-p{I}_{e}\left\{\frac{(1-\beta ){Q}^{-\beta }}{\alpha (a-bp)}\right\}-\frac{{c}_{h}{(\gamma -\beta )Q}^{\gamma -\beta }}{\alpha \left(a-bp\right)}\right]\right]\\&\quad+\left[\frac{2{Q}^{-2\beta }}{{\alpha }^{2}{(a-bp)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}+\frac{\beta {Q}^{-1-\beta }}{\alpha (a-bp){\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\quad\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]\end{aligned}$$

(41)

Differentiating Eq. (39) with respect to B we get

$$\begin{aligned}\frac{\partial {G}_{2}}{\partial B}&= \left[-\frac{{c}_{b}}{\alpha \delta \left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}\right]\\&\quad+\frac{2}{\alpha \delta {\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{2}}\left[c-p-pM{I}_{e}-\frac{B{c}_{b}}{\alpha \delta }+\frac{{c}_{l}(1-\delta )}{\delta }\right]\\&\quad+\left[\frac{2}{{\alpha }^{2}{\delta }^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}\right]\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }\right.\\&\left.\quad+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]\end{aligned}$$

(42)

Differentiating Eq. (40) with respect to p we get

$$\begin{aligned}\frac{\partial {G}_{3}}{\partial p}&=\left[-\frac{2b{Q}^{1-\beta }}{\alpha \left(1-\beta \right){\left(a-bp\right)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\quad\left[Q-B-p{I}_{e}\left[\frac{b{Q}^{2-\beta }}{\alpha {\left(a-bp\right)}^{2}\left(2-\beta \right)}\right]\right.\\&\left.\quad+{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}\right)\right]-\frac{b{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{2}\left(\gamma +1-\beta \right)}\right]\\&\quad+\left[\frac{1}{\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}\left[p{I}_{e}\left[\frac{-{2{b}^{2}Q}^{2-\beta }}{\alpha {\left(a-bp\right)}^{3}\left(2-\beta \right)}\right]\right.\right.\\&\left.\left.\quad+{2I}_{e}\left[-\frac{b{Q}^{2-\beta }}{\alpha {\left(a-bp\right)}^{2}\left(2-\beta \right)}\right]-\frac{2{b}^{2}{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha {\left(a-bp\right)}^{3}\left(\gamma +1-\beta \right)}\right]\right]\\&\quad+\left[\frac{2{b}^{2}{Q}^{2-2\beta }}{{\alpha }^{2}{\left(a-bp\right)}^{4}{\left(1-\beta \right)}^{2}{\left(\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}-\frac{B}{\alpha \delta }\right)}^{3}}\right.\\&\left.\quad-\frac{2{b}^{2}{Q}^{1-\beta }}{\alpha {\left(a-bp\right)}^{3}(1-\beta ){\left(\frac{{Q}^{1-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)}-\frac{B}{\alpha \delta }\right)}^{2}}\right]\\&\quad*\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }\right.\\&\left.\quad-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]\end{aligned}$$

(43)

Case-3:

$$\begin{aligned}{TP}_{3}(Q, B, p)&=\left[\left(p-c\right)\left(Q-B\right)-{c}_{o}-\frac{{B}^{2}{c}_{b}}{2\alpha \delta }\right.\\&\left.\quad+\frac{{c}_{l }\left(1-\delta \right)B}{\delta }-\frac{{c}_{h}{Q}^{\gamma +1-\beta }}{\alpha \left(a-bp\right)\left(\gamma +1-\beta \right)}\right.\\&\left.\quad+p{I}_{e}\left[-BM+\left(\frac{{Q}^{2-\beta }}{\alpha \left(a-bp\right)\left(1-\beta \right)\left(2-\beta \right)}\right)\right.\right.\\&\left.\left.\quad+Q\left(M-\frac{{Q}^{1-\beta }}{\alpha (a-bp)(1-\beta )}\right)\right]\right]\end{aligned}$$

(44)

The total profit function is same as Case-2; therefore, all the derivatives and corresponding results will be the same.

5 Numerical Example

The following values has been considered for the input parameters: c_o = $ 40/order, c = $ 58/unit, c_h = $ 11/unit/year, γ = 1.1, β = 0.4, $\alpha = 120$, δ = 0.83, I_p = 12%/year, I_e = 10%/year, M = 0.04 year, c_b = $ 20/unit/year, c_l = $ 6/unit/year, a = 200, b = 3.

The optimal solution is given by t₁^* = 0.0324315, T^* = 0.985543, Q^* = 3.27527, B^* = −65.8583, p^* = $66.6564/unit.

It corresponds to case-2, therefore, TP (Q^*, B^*, p^*) = $ 25.184.

6 Sensitivity Analysis

This section does an analysis of the preceding numerical example to study the effect of underestimation or overestimation of the input parameters on the optimal values of Q, p, t₁, B, T and the total profit TP (Q, B, p). It is done by varying the parametric values between 20% and −20%. The following results are drawn from the table mentioned below:

• 1. It is clear from the data that with the increasing vales of $\alpha$, the optimal order quantity (Q) increases and the ending level of inventory quantity (B) decreases. The total profit decreases.

• 2. It is observed that with the increase in value of (c_o), optimal order quantity decreases. Optimal ending level of inventory (B), t₁, T, and optimal price (p) increases. Hence, total profit increases.

• 3. It is to be pointed that with the increment in values of holding cost (c_h), the optimal order quantity (Q) decreases whereas the ending inventory level (B) increases. Optimal price (p) does not vary much but total profit increases.

• 4. With the increasing values of (c_l), it is observed that the optimal order quantity (Q) increases for some time and then start decreasing. Optimal ending inventory level (B), optimal price (p), and total profit start decreasing in the beginning and then start rising up.

• 5. With the increment in value of γ, ending inventory level (B) increases. Optimal stock (Q) decreases but total profit increases (Table 1).

  Table. 1 Sensitivity analysis by changing the input parameters

7 Conclusion

This paper highlights the following important facts: (i) display of product in large quantities enhances its demand within the customers, (ii) price is also an important factor on which demand of a product depends, (iii) holding cost is not always linearly dependent on stock. The retailer’s optimal strategy is examined in this paper based on nonlinear demand and nonlinear holding cost of his or her product when the supplier uses a policy of trade credit for its customers. An inventory model is portrayed with nonlinear demand as well as nonlinear holding cost relaxing the ending-zero inventory level condition, in which shortages occur and demand during that time is partially backlogged which helps the retailer in running his or her business. The main objective is to determine the optimal order quantity (Q), ending level of inventory (B), and optimal rice (p) in order to maximize the total profit earned per unit time by the retailer.