15.1 Introduction

Hypernuclei are many body systems consisting of ordinary nucleons and one or more strange hyperons. Recently a large number of hypernuclei are produced experimentally and the studies on hypernuclei have received a lot of attention. Hyperons are strange baryons. One of the characteristic features of the hyperon is that it is free from Pauli’s exclusion principle, which makes it easy to deeply penetrate into the nuclear interior.

The observation of first hypernuclear fragment was made by Danysz and Pniewski [1] in 1952, which was a boron nucleus in which a neutron was replaced by a \( \Lambda \) hyperon. Various properties of hypernuclei have been studied since its first evidence [2,3,4,5,6,7,8]. The stability of hypernuclei can be understood by studying its binding and separation energies. Different theoretical methods are proposed for studying the binding and separation energies of hypernuclei [9,10,11,12,13,14,15,16,17]. The decay studies of hypernuclei suggest that within the nuclear environment because of Pauli’s blocking effect, non-mesonic decay modes are dominant over the mesonic decay modes. The possibilities of decays of excited hypernuclei triggered by strong interactions [18,19,20,21] have also been a subject of study.

An extended BWMF for finding the binding energies of \( \Lambda \) hypernuclei and a new formula for obtaining the separation energies are presented. The alpha and cluster decays from hyper Po, hyper Ra, and hyper Ac nuclei are performed using the Coulomb and proximity potential model (CPPM) [22] with the inclusion of a \( \Lambda \)-nucleus potential.

Since the superheavy elements up to Z \(=\) 118 have been confirmed in the laboratory, the study of SHE with Z > 118 now becomes an important topic in the nuclear physics research. SHEs were synthesized via two methods; hot fusion reaction at JINR-FLNR, Dubna for Z \(=\) 114−118 [23,24,25,26,27,28] and cold-fusion reaction at GSI, Darmstadt and at RIKEN, Japan for Z \(=\) 102−112 [29, 30]. The element Z \(=\) 113 was synthesized successfully by hot fusion reaction using \( ^{48} \)Ca \(+\) \( ^{237} \)Np by Oganessian et al. [31] and by cold-fusion reaction using \( ^{70} \)Zn\(+\) \( ^{209} \)Bi by Morita et al. [32]. However, it is difficult to produce SHE with Z \(=\) 113 in cold-fusion reactions because of the smaller production cross sections. The discovery of superheavy nuclei in the fusion reactions of \( ^{48} \)Ca \(+\) \( ^{238} \)U \( \rightarrow \) \( ^{249} \)Cf were reviewed by Oganessian and Utyonkov in 2015 [33]. Recently Khuyagbaatar et al. [34] predicted the ER cross section for the isotope of Ts (Z \(=\) 117) for which the experiment was performed at the gas-filled recoil separator TASCA and confirmed the previous findings at the Dubna Gas-Filled Recoil Separator [25, 26, 35].

The ER residue cross section depends on the projectile-target pair, center-of-mass energy which in turn depends on probability of CN formation, excitation energy, fission barrier of CN, and survival probability. Hence, the predictions of the favorable reactions and beam energy are very important for the synthesis of superheavy elements. In the present paper, we have studied the decay modes and production cross section for the SHE with Z \(=\) 121. The evidence for the synthesis of Z \(=\) 121 is not reported yet and this study may helpful for future experimental investigations.

15.2 Theory

15.2.1 Methodology to Study the Properties of Hypernuclei

The lambda–nucleon (\( \Lambda \)N) interaction inside a hypernucleus can be understood by studying its binding and separation energies. Different formalisms are there for studying the properties of hypernuclei. One among them is the use of semi-empirical methods for evaluating the binding and separation energies.

In a recent study [36], we have proposed a new semi-empirical formula, by extending the Bethe–Weizsäcker mass formula (BWMF), for calculating the binding energy of singe \( \Lambda \) hypernuclei, which is given by

$$\begin{aligned} B(N,Z, \Lambda ) = a_{v}A_{c}-a_{s}A_{c}^{2/3}-a_{c}\frac{Z(Z-1)}{A_{c}^{1/3}}-a_{sym}\frac{(N-Z)^{2}}{A_{c}}+\delta -\frac{b_{0}}{A^{2/3}}\left[ 1-\frac{b_{1}}{A^{2/3}}\right] +b_{2}. \end{aligned}$$
(15.1)

Here A is the mass number of the hypernucleus, given by, A \(=\) Z \(+\) N \(+\) \( \Lambda \), and \( A_{c} \) is the mass number of core nucleus, \( A_{c}= Z + N \), where Z and N are the number of protons and number of neutrons. \( a_{v} \), \( a_{s} \), \( a_{c} \) and \( a_{sym} \) are the usual BWMF constants, given by, \( a_{v} =\) 15.79 MeV, \( a_{s} =\) 18.34 MeV, \( a_{c} =\) 0.71 MeV, \( a_{sym} =\) 23.21 MeV. \( \delta \) is the pairing term, which is \( 12A_{c}^{-1/2} \) for even N even Z nuclei, \( -12A_{c}^{-1/2} \) for odd N odd Z nuclei and 0 otherwise. \( b_{0} \), \( b_{1} \) and \( b_{2} \) are given as, \( b_{0} =\) 119.445 MeV, \( b_{1} =\) 1.119 MeV, \( b_{2} =\) 33.047 MeV.

A new formula is also suggested [36] using the least square regression to the updated experimental data of single \( \Lambda \) hypernuclei, given as

$$\begin{aligned} S_{\Lambda }=a_{0}+\frac{a_{1}}{A^{2/3}}+\frac{a_{2}}{A^{4/3}}. \end{aligned}$$
(15.2)

Here \( a_{0} = 28.442\) MeV, \( a_{1} = -119.445\) MeV and \( a_{2} =133.651\) MeV.

These two new formulae for the binding and separation energies of \( \Lambda \) hypernuclei are found to be more suitable for obtaining the experimental results as well as for making theoretical predictions [36].

Another important part in the studies of hypernuclei is the decay of hypernuclei. Even though many studies have been put forward for studying the weak decay of hypernuclei, only a few numbers of studies [18,19,20,21] have been performed on the hypernuclear decay triggered by strong interaction, such as alpha and cluster emission. We have modified the Coulomb and proximity potential model (CPPM) proposed by Santhosh et al. [22] with the inclusion of a \( \Lambda \)-nucleus potential, for studying the alpha and cluster emissions from hypernuclei. In CPPM, the interacting potential between two nuclei is taken as the sum of Coulomb potential, proximity potential, and centrifugal potential. It is given by

$$\begin{aligned} V=\frac{Z_{1}Z_{2}e^{2}}{r}+V_{p}(z)+\frac{\hbar ^{2}l(l+1)}{2\mu r^{2}}, \quad for \; z>0. \end{aligned}$$
(15.3)

Here \( Z_{1} \) and \( Z_{2} \) are the atomic numbers of the daughter and emitted cluster, r is the distance between fragment centers, z is the distance between the near surfaces of the fragments, l represents the angular momentum and \( \mu \) the reduced mass. \( V_{p} \) is the proximity potential given by Blocki et al. [37, 38] as

$$\begin{aligned} V_{p}(z)=4\pi \gamma b\left[ \frac{C_{1}C_{2}}{C_{1}+C_{2}} \right] \Phi \left( \frac{z}{b} \right) \end{aligned}$$
(15.4)

with the nuclear surface tension coefficient,

$$\begin{aligned} \gamma = 0.9517 \left[ 1-1.7826\frac{(N-Z)^{2}}{A^{2}}\right] MeV/fm^{2}. \end{aligned}$$
(15.5)

Here N, Z, and A represent the neutron, proton, and mass number of the parent nuclei. \( \Phi \) represents the universal proximity potential [38] and \( C_{i} \) is the Süsmann central radii of the fragments.

The potential for the internal part (overlap region) of the barrier is given as

$$\begin{aligned} V=a_{0} (L-L_{0})^{n},\quad for\; z<0, \end{aligned}$$
(15.6)

where \( L=z+2C_{1}+C_{2}\) fm and \( L_{0} =2\) C fm. The constants \( a_{0} \) and n are determined by the smooth matching of the two potentials at the touching point.

The barrier penetrability P using the one dimensional Wentzel–Kramers–Brillouin approximation, is given as

$$\begin{aligned} P=exp\left\{ -\frac{2}{\hbar }\int _{a}^{b}\sqrt{2\mu (V-Q)}dz\right\} . \end{aligned}$$
(15.7)

Here the mass parameter is replaced by \( \mu = \frac{mA_{1}A_{2}}{A} \), where m is the nucleon mass and \( A_{1} \), \( A_{2} \) are the mass numbers of daughter and emitted cluster, respectively. The turning points ‘a’ and ‘b’ are determined from the equation,\( V (a) = V (b) = Q \), where Q is the energy released. The half-life time is given by

$$\begin{aligned} T_{1/2}=\left( \frac{ln 2}{\lambda } \right) =\left( \frac{ln 2}{\nu P} \right) . \end{aligned}$$
(15.8)

Here \( \lambda \) is the decay constant and \( \nu \) is the assault frequency. The empirical vibration energy \( E_{\nu } \), is given as [39]

$$\begin{aligned} E_{\nu }=Q\left\{ 0.056+0.039 exp\left[ \frac{\left( 4-A_{2} \right) }{2.5} \right] \right\} , for \, A_{2} \ge 4 \end{aligned}$$
(15.9)

To incorporate the changes in potential due to \( \Lambda \) particle, we have included the potential, \( V_{\Lambda } \) between the non-strange normal fragment and the fragment that contains lambda particle, in the expression for the interacting potential (15.3). That is, as the alpha particle penetrates the potential produced by the Coulomb force, nuclear force, and centrifugal force, it also feels the potential generated by the \( \Lambda \) hyperon. The potential, \( V_{\Lambda } \) between the non-strange and strange fragments is given by

$$\begin{aligned} V_{\Lambda }=\int \rho _{\Lambda }(r_{1})V_{\Lambda N}\left( r_{1} - r\right) d^{3}r_{1}, \end{aligned}$$
(15.10)

where \( \rho _{\Lambda }(r_{1}) \) is the density distribution of \( \Lambda \) particle. The density distribution of \( \Lambda \) particle is taken from the [40, 41] and has the form,

$$\begin{aligned} \rho _{\Lambda }(r)=\left( \pi b_{\Lambda }^{2}\right) ^{-3/2} e^{-r^{2}/b_{\Lambda }^{2}}. \end{aligned}$$
(15.11)

Here \( b_{\Lambda }=\sqrt{\frac{4M_{N}+M_{\Lambda }}{4M_{\Lambda }b_{\alpha }}} \), where \( M_{N} \) and \( M_{\Lambda } \) are the mass of the nucleon and \( \Lambda \) particle, respectively, and \( b_{\alpha } = 1.358\) fm. The lambda-nucleon force is short range and the strength of lambda-nucleus potential \( V_{\Lambda N} \) is smaller than the nucleon-nucleus potential. The lambda-nucleus potential, \( V_{\Lambda N} \), is taken from [42] and is given by,

$$\begin{aligned} V_{\Lambda N}=\frac{V_{0}}{1+exp \left[ \frac{r-c}{a} \right] }. \end{aligned}$$
(15.12)

Here the constants \( V_{0} = -27.4\) MeV, \( a = 0.6\) fm and \( c = 1.08A^{1/3} \). By including the lambda-nucleus potential in (15.3), the half-lives for the hypernuclei can also be determined using (15.8).

15.2.2 Methodology to Find Decay Modes and Production Cross Section of SHE

The cross section of SHE production in a heavy-ion fusion reaction with subsequent emission of x neutrons is given by

$$\begin{aligned} \sigma _{ER}^{xn}=\frac{\pi }{k^{2}}\sum _{l=0}^{\infty } \left( 2l+1 \right) T(E,l) P_{CN}(E,l)W_{sur}^{xn}(E^{*},l). \end{aligned}$$
(15.13)

The probability of compound nucleus formation [43,44,45] is given as

$$\begin{aligned} P_{CN}\left( E, l \right) = \frac{exp\left\{ -c \left( x_{eff}-x_{thr}\right) \right\} }{1+exp\left\{ \frac{E_{B}^{*}-E^{*}}{\Delta } \right\} }, \end{aligned}$$
(15.14)

where \( E^{*}=E_{cm}-Q-\frac{l(l+1)}{2\mu r^{2}} \) is the excitation energy of the compound nucleus, \( E_{B}^{*} \) denotes the excitation energy of the CN when the center-of-mass beam energy \( (E_{cm}) \) is equal to the Coulomb and proximity barrier, \( \Delta \) is an adjustable parameter (\(\Delta = 4\) MeV) and \( x_{eff} \) is the effective fissility defined as

$$\begin{aligned} x_{eff}=\left[ \frac{(Z^{2}/A)}{(Z^{2}/A)_{crit}}\right] \left( 1-\alpha +\alpha f(K) \right) . \end{aligned}$$
(15.15)

With \( (Z^{2}/A)_{crit} \), f(K) and K are given by

$$\begin{aligned} (Z^{2}/A)_{crit}=50.883\left[ 1- 1.7286 \left( \frac{(N-Z)}{A} \right) ^{2} \right] \end{aligned}$$
(15.16)
$$\begin{aligned} f(K)=\frac{4}{K^{2}+K+\frac{1}{K}+\frac{1}{K^{2}}} \end{aligned}$$
(15.17)
$$\begin{aligned} K=\left( \frac{A_{1}}{A_{2}} \right) ^{1/3}, \end{aligned}$$
(15.18)

where Z, N and A represent the atomic number, neutron number, and mass number, respectively. \( A_{1} \) and \( A_{2} \) are mass number of projectile and target, respectively. \( x_{thr} \), c are adjustable parameters and \( \alpha =1/3 \). The best fit to the cold-fusion reaction, the values of c and \( x_{eff} \) are 136.5 and 0.79, respectively. For hot fusion reaction, the best fit for \( x_{eff} \le 0.8 \) is \( c=104 \) and \( x_{thr} =0.69 \); while \( x_{eff}\ge 0.8 \), the values are \( c = 82 \) and \( x_{thr} = 0.69 \). These constants are suggested by Loveland [44].

The survival probability \( W_{sur} \) is the probability for the compound nucleus to decay to the ground state of the final residual nucleus via evaporation of light particles and gamma ray for avoiding fission process. The survival probability under the evaporation of x neutrons is

$$\begin{aligned} W_{sur}=P_{xn}(E_{CN}^{*})\prod _{i=1}^{i_{max}=x}\left( \frac{\Gamma _{n}}{\Gamma _{n}+\Gamma _{f}}\right) _{i, E^{*}} , \end{aligned}$$
(15.19)

where the index i is equal to the number of emitted neutrons, \( P_{xn} \) is the probability of emitting exactly xn neutrons [46], \( E^{*} \) is the excitation energy of the compound nucleus, \( \Gamma _{n} \) and \( \Gamma _{f} \) represent the decay width of neutron evaporation and fission, respectively. To calculate \( \Gamma _{n}/\Gamma _{f} \), Vandenbosch and Huizenga [47] have suggested a classical formalism:

$$\begin{aligned} \frac{\Gamma _{n}}{\Gamma _{f}} = \frac{4A^{2/3}a_{f}\left( E^{*}-B_{n} \right) }{K_{0}a_{n}\left[ 2a_{f}^{1/2} \left( E^{*}-B_{f} \right) ^{1/2}-1 \right] } exp \left[ 2a_{n}^{1/2}\left( E^{*}-B_{n} \right) ^{1/2} -2a_{f}^{1/2} \left( E^{*}-B_{f} \right) ^{1/2} \right] , \end{aligned}$$
(15.20)

where A is the mass number of the nucleus considered, \( E^{*} \) is the excitation energy, and \( B_{n} \) is the neutron separation energy. The constant \( K_{0} \) is taken as 10 MeV. \( a_{n}=A/10 \) and \( a_{f}=1.1a_{n}\), are the level density parameters of the daughter nucleus and the fissioning nucleus at the ground state and saddle configurations, respectively, and \( B_{f} \) is the fission barrier. The alpha decay half-lives are calculated using the modified generalized liquid drop model (MGLDM) [48] of our group and spontaneous fission half-lives are calculated using the formula of Santhosh et al. [49]

$$\begin{aligned} log\left( T_{1/2} / yr\right) = a \frac{Z^{2}}{A}+b\left( \frac{Z^{2}}{A}\right) ^{2} + c\left( \frac{N-Z}{N+Z}\right) +d \left( \frac{N-Z}{N+Z}\right) ^{2}+eE_{shell}+f, \end{aligned}$$
(15.21)
Fig. 15.1
figure 1

Plot of BE/A versus mass number for all the experimentally synthesized \( \Lambda \) hypernuclei

Full size image

where \( a = -43.25203 \), \( b = 0.49192 \), \( c = 3674.3927 \), \( d = -9360.6 \), \( e = 0.8930 \), and \( f = 578.56058 \). \( E_{shell} \) is the shell correction energy.

15.3 Results and Discussion

The BWMF for hypernuclei is an extension of BWMF of normal nuclei to the hypernuclear sector. The formula was developed by studying the variation of binding energy for all the experimentally identified \( \Lambda \) hypernuclei with \( A^{-2/3} \). It was seen that there exists an asymptotic relation between the binding energy and the hypernuclear surface term, which is proportional to \( A^{2/3} \). The performance of the newly proposed mass formula (15.1) has been demonstrated by evaluating the binding energies of all the thirty-five experimentally synthesized \( \Lambda \) hypernuclei from \( _{\Lambda }^{4} H \) to \( _{\Lambda }^{208} Pb \) [50,51,52,53,54,55]. The predictive power of the new formula has been revealed by evaluating the standard deviation. As compared to other theoretical formalisms, the new formula gives the minimum standard deviation. Figure 15.1 shows the variation of BE/A using (15.1) with the mass number for the experimentally synthesized \( \Lambda \) hypernuclei. A comparison with the experimental results is also given. The formula proposed for finding the separation energy (15.2) also gives better agreement with experimental data as compared to other theoretical formalisms. Figure 15.2 shows the plot of separation energy obtained using (15.2) versus mass number of \( \Lambda \) hypernuclei. The agreement between theoretical predictions and the experimental observations can be seen from the figure.

Fig. 15.2
figure 2

Plot of separation energy versus mass number for all the experimentally synthesized \( \Lambda \) hypernuclei

Full size image

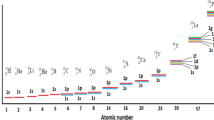
Considering to the decay of hypernuclei triggered by strong interaction, we have studied alpha emission from hyper Po nuclei, alpha, and cluster emission from hyper Ra nuclei and hyper Ac nuclei using CPPM with the inclusion of a \( \Lambda \)-nucleus potential. The elements Po, Ra, and Ac are well-known members of natural radioactive series. Since many isotopes of these elements are good alpha emitters, their corresponding hypernuclei may also exhibit alpha decay. The half-lives of alpha emission from hyper \( ^{187-224}{_{\Lambda }Po} \) are calculated. It was found that the isotopes \( ^{187-224} {_{\Lambda }Po} \) exhibit alpha decay. Similarly, while studying the alpha emission from \( ^{202-235} {_{\Lambda }Ra} \) nuclei, it was seen that the alpha half-lives of \( ^{202-231} {_{\Lambda } Ra} \) are within the experimental limit. Also the half-lives for \( ^{14}C \) emission from \( ^{217-229} {_{\Lambda }Ra} \) are favorable for measurement. Studies on hyper Ac nuclei showed that \( ^{207-234} {_{\Lambda }Ac} \) nuclei are unstable against alpha decay. It is also seen that \( ^{14}C \) emission from \( ^{218-229} {_{\Lambda }Ac} \) are favorable for measurement. Figure 15.3 gives the plot for neutron number versus \( log_{10}T_{1/2} \) of various alpha emitting isotopes of hyper Po, hyper Ra, and hyper Ac. The \( ^{14}C \) emission from various isotopes of hyper Ra and hyper Ac is depicted in Fig. 15.4. The proton and neutron shell closures at Z \(=\) 82 and N \(=\) 126 are revealed through the hypernuclear decay studies.

Fig. 15.3
figure 3

Plot of \( log_{10}T_{1/2} \) versus neutron number of parent for various alpha emitting isotopes of hyper Po, hyper Ra, and hyper Ac

Full size image
Fig. 15.4
figure 4

Plot of \( log_{10}T_{1/2} \) versus neutron number of parent for various \( ^{14}C \) emitting isotopes of hyper Ra and hyper Ac

Full size image

The decay modes of SHE \( ^{302-304,306}121 \) are investigated by comparing the \( \alpha \)-decay half-lives with the spontaneous fission half-lives and the calculated values are shown in Table 15.1. The \( \alpha \)-decay half-lives are calculated using MGLDM [48] and SF half-lives calculated using semi-empirical relation given by Santhosh et al. [49]. The nuclei with \( \alpha \)-decay half-lives shorter than spontaneous fission half-lives will survive fission and hence decay through \( \alpha \) emission. It is found that isotopes \( ^{306,304-302}121 \) exhibit 3 alpha chains followed by SF.

Table 15.1 Decay modes of SHEs \( ^{302-304,306}121.\) Half − lives are in seconds
Full size table
Fig. 15.5
figure 5

ER cross section in 2n, 3n, 4n and 5n evaporation channel

Full size image

The ER cross section in 2n, 3n, 4n, and 5n evaporation channel for the synthesis of isotopes \( ^{302-304,306}121 \) using the reactions, \( ^{50}Ti+^{252}Es\rightarrow ^{302}121 \), \( ^{54}Cr+^{249}Bk\rightarrow ^{303}121 \),\( ^{50}Ti+^{254}Es\rightarrow ^{304}121 \), and \( ^{48}Ca+^{258}Md \rightarrow ^{306}121 \) are studied. The corresponding figures representing ER cross section in each evaporation channel is presented in Fig. 15.5. The largest ER cross section obtained in each evaporation channel is listed in Table 15.2. It is found that, the 2n and 3n channel cross section is more for the reaction \( ^{50}Ti+^{252}Es\rightarrow ^{302}121 \), and 4n channel cross section is more for the reaction \( ^{50}Ti+^{254}Es\rightarrow ^{304}121 \).

Table 15.2 Maximum value of ER cross section obtained in each evaporation channel
Full size table

15.4 Conclusion

The binding and separation energies of \( \Lambda \) hypernuclei are predicted using two new formalisms. The values predicted using the new formulae are in good agreement with the experimental results. These two simple formulae provide a reliable method for finding the two important quantities of hypernuclei, that is, the binding energy and the separation energy. The hypernuclear decay triggered by strong interactions, particularly the alpha and the cluster emissions are studied using CPPM with the inclusion of a \( \Lambda \)-nucleus potential for the isotopes of hyper Po, hyper Ra, and hyper Ac. The study shows that the alpha and cluster decay half-lives of many of the isotopes of these hyper elements are within the experimental limit. The proton and neutron shell closure at Z \(=\) 82 and N \(=\) 126 in the hypernuclear region is also revealed from the study.

We have predicted the alpha decay half-lives and SF half-lives of the isotope SHE \( ^{302-304,306}121 \). The isotopes \( ^{302-304,306}121 \) shows 3 alpha chains followed by SF and hence these isotopes can be synthesized and detected in the laboratory. The studies on ER cross section for the synthesis of these isotopes using the reactions, \( ^{50}Ti+^{252}Es \rightarrow ^{302}121 \), \( ^{54}Cr+^{249}Bk \rightarrow ^{303}121 \),\( ^{50}Ti+^{254}Es \rightarrow ^{304}121 \) and \( ^{48}Ca+^{258}Md \rightarrow ^{306}121 \) are performed and it is clear that the reactions \( ^{50}Ti+^{254}Es \rightarrow {}^{304}121 \), and \( ^{50}Ti+^{252}Es \rightarrow ^{302}121 \) have maximum probability in 3n and 4n channel, respectively.We hope that our studies on hypernuclei and superheavy elements will be a guide line for further investigations in these fields.