Sequencing of Practice Examples for Mathematical Reasoning: A Case of a Singapore Secondary School Teacher’s Practice

Abstract

Variation of examples is a common technique some teachers use in the design of their instructional materials. It is, however, not clear how mathematical reasoning can be supported through teachers’ carefully selected examples. Through a case study of an experienced and competent Singapore secondary school mathematics teachers who emphasised “reasoning” as a specific goal of his instructional practice, we examine how practice examples were designed to target reasoning in the teaching of mathematics. In particular, the study unpacks how mathematical reasoning can be utilised as a glue in advancing a canonical technique alongside the development of supportive lesson routines. The findings showed the following four design principles (i) Deliberate use of examples to advance technique (ii) Advance technique through comparing, inferring and justifying (iii) Special cases to expose and target students’ faulty reasoning undergirding the techniques they used (iv) Consolidate and formalise the reasoning in standard written form through whole class instructional segment.

1 Introduction

We are part of the project team (see Chapter 2) that aims to distil the distinctive features of mathematics teaching in Singapore classrooms. In the course of our data collection, the manner in which examples were used by Teacher 13 particularly caught our attention. Teacher 13’s use of examples was not merely for achieving fluency of technique; his other ostensible goal was to use the examples to “advance” (a term he used) mathematical “reasoning”—a term he used very often in his interviews with us and in his classroom teaching. As we studied the numerous instances in which the examples were used to encourage students’ reasoning, we found that Teacher 13’s conception of these examples and how they were utilised in his classroom work presented aspects that are still unreported in the current literature.

2 Use of Examples

Before we examine the case of Teacher 13’s use of examples to advance reasoning, we turn to the literature that relates to this focus of study. In particular, we review literature on task design, variation theory in the sequencing of tasks and practice examples.

2.1 Task Design

Mathematical tasks are important vehicles for building student capacity for mathematical thinking and reasoning (Stein, Grover, & Henningsen, 1996). The recently published ICMI Study 22 on Task design in mathematics education presents an up-to-date summary of relevant research about task design in mathematics education. While there are advances in knowledge in areas, such as multiple frameworks and sets of principles on task design—the design and implementation of task sequences is one of the key areas identified as still needing further research (Watson & Ohtani, 2015). In this study, we limit the discussion on tasks with the ostensible goal of students’ reasoning. Smith and Stein’s (1998) categorisation of tasks to different levels of cognitive demands where the extent to which students engage in thinking and reasoning differ in each level is relevant and influential. However, there is yet little research on how tasks or a sequence of tasks can be employed to help students advance their reasoning in the process of working through these tasks.

2.2 Sequences of Tasks and Variation Theory

In the design principles behind the design of task sequences, there is major contribution in the literature from Variation Theory (VT). In the design of task sequences, “VT focuses task designers on what varies and what remains invariant in a series of tasks in order to enable learners to experience and grasp the intended object of learning” (Kieran, Doorman, & Ohtani, 2015, p. 45). Watson and Mason (2006) claimed that “tasks that carefully display constrained variation are generally likely to result in progress in ways that unstructured sets of tasks do not, as long as learners are working within mathematically supportive learning environments” (p. 92). Their paper illustrates how differently controlled variations can help students make different generalisations and abstractions—generalisations as “sensing the possible variation in a relationship” and abstractions as “shifting from seeing relationships as specific to the situation, to seeing them as potential properties of similar situations” (p. 94).

Watson and Mason’s (2006) study reported a rare venture within the tradition of VT-focusing on the mathematical content as the only “object of learning”- and they explain “generalisations” that are afforded by a particular way of sequencing tasks. This shift to “generalisations” brings this branch of VT-related research closer to our inquiry on mathematical reasoning. In fact, we do not find mathematical reasoning an explicit goal in much of the research reported under the banner of VT. Another recent rare connection of reasoning to VT was reported by Vale, Widjaja, Herbert, Bragg, and Loong (2017). They showed how justification or logical argument fits into this sequence of learning experiences by mapping the variation in children’s reasoning (e.g., comparing and contrasting to generalise and identifies verifying) in number commonality problems. Their findings reiterated the importance of designing the task so that the action of comparing and contrasting guides student awareness of features that matter. Their paper, however, does not unpack the deliberate task sequencing for the purpose of advancing students’ mathematical reasoning.

For the purpose of this study, instead of using “task” which is a very board category, we employ Teacher 13’s use of “examples” which we take to be a special type of tasks. We think that examples are tools to provide variation to aid students’ reasoning. Examples, especially “combination of several similar examples and further not-quite similar examples” are necessary for students “to work on a higher level” that leads to conceptual learning, fluency and accuracy (Watson & Mason, 2006, p. 97).

2.3 Practice Examples

From a mathematical perspective, an example is often considered an object satisfying certain conditions (e.g., Alcock & Inglis, 2008; Watson & Mason, 2005), or a representative of a class (e.g., Mills, 2014; Zazkis & Leikin, 2007). Zaslavsky (2014) adds a requirement that the person using the example should be able to answer the question: “What is this an example of?” (Zaslavsky, 2019, p. 246)

Zodik and Zaslavsky (2008, p. 165) referred to examples as “a particular case of a larger class, from which one can reason and generalise”. Their treatment of examples included non-examples that are “associated with conceptualisation and definitions, and serve to highlight critical features of a concept; as well as counter-examples that are associated with claims and their refutations” (p. 165). “Mathematical objects only become examples when they are perceived as examples of something: conjectures and concepts, application of techniques or methods …” (Goldenberg & Mason, 2008, p. 184). That is, examples may differ in their nature. An example of a concept such as rational number is different in nature from an example of how to carry out a procedure (Zodik & Zaslavsky, 2008). Examples can also differ in their purpose such as to illustrate how to find a common denominator of two proper fractions for adding fractions, or to illustrate it so as to generalise the procedure to algebraic fractions to solve more advanced equations (Zodik & Zaslavsky, 2008). Rowland (2008)’s work informed us of possible considerations in the choice and selection of examples; variation to be experienced by the learners in accordance to Marton and colleagues’ (2004) Theory of Variation. Zodik and Zaslavsky (2008) also suggested some considerations when teachers select or generate examples.

Two different use of examples in teaching were reported by Rowland (2008). The first use is inductive—providing examples of something and the examples are “particular instances of the generality” (Rowland, 2008, p. 150). The second use is not inductive, but for the purpose of practice and is often referred to as “exercises”. To illustrate this use: students learnt the procedures to find equivalent fractions and then rehearsed and worked on the “exercise” so that they could remember it through repetition and eventually developed fluency of the procedures. Examples used in this way was “for practice”, also known as practice examples in that they are “vehicle for [students] to gain fluency with the algorithm” (Rowland, 2008, p. 158).

In this chapter, we define Teacher 13’s sequence of practice examples as a carefully selected set of examples meant to fulfil his instructional goals. Reminded by Zaslavsky (2019), we specify or define practice examples by referring to the goals, “what is it an example of?”. In Teacher 13’s case, his practice examples were

• 1. For the purpose of practice to gain fluency by an underlying technique;

• 2. They are thus examples of the technique; and

• 3. As a set of vehicles to advance reasoning (This will be detailed in the analysis later).

3 Method

3.1 Context

Teacher 13 was identified as an experienced and competent teacher. An “experienced” teacher is one who has taught the same mathematics course at the same level for a minimum of five years; and “competent” selection is based on recognition by the local professional community as a teacher who is effective in teaching mathematics. Below, we summarise a number of factors about Teacher 13’s practices that lends itself to an unpacking of his reasoning work:

• 1. Teacher 13’s repeated reference to “reasoning” in interviews articulating comprehensively his goals for the tasks in his instructional materials and his classroom discourse determined our choice of Teacher 13 as a case study of mathematical reasoning—a characteristic feature of case study.

• 2. A full set of handouts (instructional material) for students use in class (hereafter referred to as “Notes”) was developed with his colleagues before the start of the module.

• 3. He constantly made references between his goals, his actual activity in class, and his use of instructional materials. This enables us to study the interactions among these major pieces of his instructional processes.

3.2 Teacher 13’s Class and Students

The class in which we recorded his teaching consisted of 20 students aged between 14 and 16. They were in their third year—akin to Year 9—of a six-year Integrated Programme (IP). In Singapore, there are various education paths students can choose to take after they complete six years of elementary school. Of which, students in the IP pursues a six-year course which integrates the four-year secondary and two-year pre-university education programmes.

3.3 Topic

The module that Teacher 13 taught was “Quadratic Graphs and Inequalities” over 10 lessons. The coverage includes from Ministry of Education (2012):

• 1. Solve quadratic equations in one variable using: (i) the general formula, (ii) completing the square and (iii) graphical method;

• 2. State the conditions for a quadratic equation to have: (i) two real roots, (ii) two equal roots and (iii) no real roots;

• 3. State the conditions for $ax^{2} + bx + c$ to be always positive (or always negative); and

• 4. Solve quadratic inequalities, and represent the solution: (i) using a graph, and (ii) on the number line.

4 Data and Analysis

4.1 Data

The instructional materials used by Teacher 13 were mainly the Notes and questions from the textbooks (Yeo, Teh, Loh, & Chow, 2013; Yeo et al., 2015) (as homework) for the students. These instructional materials form the primary source of data. The next data source are the interviews conducted with Teacher 13—one pre-module interview before his lessons and three post-lesson interviews after three lessons he selected (Lessons 3, 6 and 8). All interviews were video recorded. The pre-module interview was conducted to mainly find out Teacher 13’s instructional goals and how he designed and planned to utilise his instructional materials to fulfil his goals. Examples of the pre-module interview questions were:

• Please share with us some of the goals for this series of lessons. You can include both content and non-content goals.

• Are there any specific difficulties you anticipate that some of your students may have with some of the instructional materials?

The post-lesson interviews were conducted to find out if he had met his instructional objectives with the instructional materials he designed and planned to use. Examples of the questions were:

• What were the design principles you used in the instructional materials?

• What do you have in mind when you designed this/these item(s)? What learning experience(s) do you want your students to go through?

The third source of data is Teacher 13’s enactment of his lessons in the module. We adopted non-participant observer roles during the course of our study—one researcher sat at the back of the class to observe Teacher 13’s lessons—for the researcher to make relevant and specific references to his teaching actions when pursuing certain threads during the post-lesson interviews. A video camera is also placed at the back of the class to record Teacher 13’s actions. A total of 10 lessons were video recorded for Teacher 13.

4.2 Analysis

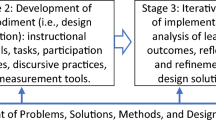
We proceeded with our analysis illustrated in Fig. 13.1.

Fig. 13.1

Analysis procedure

Stage 1: Identification of Units of Analysis of the Notes

From Teacher 13’s lessons, we noticed that the tasks, in the form of Examples, he utilised from the Notes could be grouped into units according to the method applied to solve them. In this paper we present detailed analysis of two units which contained Teacher 13’s most references to reasoning goals. They are:

• Unit 1: Examples and Practice Examples 5, 6(a), 6(b), 6(c) and 6(d)

• Unit 2: Examples and Practice Examples 10, 11 and 12

We coded Teacher 13’s classroom vignettes of the respective lessons and the responses he gave in the relevant interviews for these units of analysis. Some of the initial codes were “reasoning”, “deducing”, “comparing” and “thinking”—words Teacher 13 used often in his interviews and lessons. We then referred to Jeanotte and Kieran’s (2017) conceptual model of mathematical reasoning in which they defined mathematical reasoning as “a process of communication with others or with oneself that allows inferring mathematical utterances from other mathematical utterances” (p. 7). Eventually, we consolidated our coded data into three categories, “comparing”, “justifying” and “inferring”. Comparing and justifying were taken from Jeannotte and Kieran. We included inferring as a third category, by this we mean a conscious guessing of another step in the deductive reasoning process. In other contexts, this is equivalent to “deducing”; we avoid this latter term as it has a more restrictive use in Jeanotte and Kieran (2017). These three categories will be elaborated in the findings section to support our claim that Teacher 13 utilised his tasks to develop his students’ mathematical reasoning.

Stage 2: Composition of Chronological Narratives

For some of these selected units with related data on Teacher 13’s enactment and interview comments, we crafted chronological narratives (CN), i.e. according to timeline for each of them. In each CN, we integrated pre-module interview transcriptions, post-lesson interview transcriptions, tasks in his Notes and his classroom vignettes. The process for the composition of CN for Unit 1, for instance, began when we examined his responses in a post-lesson interview. He commented that Example 6(d) was specifically selected so that students could apply some reasoning skills; and Example 6(c) was one that required students to be able to deduce from the graph they would sketch. Hence, we studied the video clip of the corresponding lesson segments carefully for the surrounding context. We noticed that the tasks—Examples 6(c) and Example 6(d)—that required reasoning were similar to Example 5 which Teacher 13 demonstrated to his students earlier in Lesson 5. This led us to re-examine Lessons 5 and 6 with a view of Teacher 13’s agenda in helping students learn reasoning skills along the categories of comparing, inferring and justifying. We consolidated the evidence and organised them chronologically in a table. Table 13.1 shows the CN for Unit 1.

Table 13.1 Overview of the Chronological Narrative (CN) of Unit 1

Stage 3: Formation of Preliminary Design Principles related to Mathematical Reasoning

We begin our intensive source of analysis to identify themes related to how Teacher 13 embedded reasoning in Unit 1. The themes were confirmed after several rounds of discussions with several members of the research team and that the uncovered design principles were supported by the data sources.

Stage 4: Testing of Preliminary Design Principles

In the final stage of analysis, we brought the design principles we conjectured in Stage 3 and checked it against all the other CNs. Through this process, we managed to refine the initial design principles into a form that contributes to theory generalisation. In the next section, we present our findings on the processes of analysis under Stages 3 and 4 by first detailing the CN on Unit 1, followed by another CN on Unit 2. Evidences in support of these refined design principles are presented summarily in a third unit.

5 Results

5.1 Analysis of Unit 1: Researchers’ Formation of Conjectures

Conjecture 1: Advance one more

In Unit 1, the technique that Teacher 13 taught the students can be summarised into these two steps:

• Step 1: Obtain the (type of) roots (e.g., factorisation, quadratic formula, completing the square method)

• Step 2: Use graphs to visualise the region that satisfy the inequalities

The technique was applied to Examples 3 and 4 (see Fig. 13.2).

Fig. 13.2

Examples 3 and 4 in the Notes

To Teacher 13, Step 1 was merely a recall of the method of factorisation for all these items; his focus was on Step 2, how the roots of the quadratic equation were represented graphically as a visual to obtain the required regions that satisfy the required inequalities. From Teacher 13’s post-lesson interview after Lesson 6,

The first section [Example 3 & Example 4(a), (b), (c) as shown in Fig. 13.2] is easy to factorise [Step 1], just focus on using graphical method [Step 2]. Then advance one more … in Example 5. Right, what happens if we cannot factorise properly [Step 1] … (Post-Lesson Interview 2, 08:53)

Teacher 13’s “advance one more” caught our attention. Since he mentioned that “advance one more” occurred first in Example 5, we studied the example and contrasted it against earlier examples. Figure 13.3 shows Examples 5 and 6.

Fig. 13.3

Examples 5 and 6 in the Notes

On the surface, it seemed that advance one more refers to the development of the method (from factorisation to the quadratic formula) to find the roots to the quadratic equations in Step 1. Step 2 where students use graphs to visualise the regions of the solution sets remains intact. Teacher 13’s Notes pointed out explicitly that the expression given in Example 5 is not easily factorised (see Fig. 13.3).

Our analysis of Teacher 13’s enactment of this portion of the notes shows that he carefully pointed out to students that Example 5 “is the case where you cannot factorise very nicely” (Lesson 5, 25:59). Hence, an adjustment of the method to solve the quadratic equation was needed which he demonstrated using the quadratic formula. After finding the roots of the quadratic equation, he reverted back to Step 2 and emphasised, “… then you can do the usual [Step 2]. Everything else will follow the previous procedure” (Lesson 5, 28:25). Our analysis of Teacher 13’s lesson showed that the suite of examples in Example 6 was designed for students to practice their technique to solve the quadratic inequalities. He said “Example 6 gives you time to practice what to do when your quadratic expression is not very friendly - it doesn’t factorise nicely. OK? So for simple ones, can you just try 6(a)”. (Lesson 05, 34:00).

It becomes clear to us that Teacher 13’s “advance one more” carried on to the “special cases” of Examples 6(c) and 6 (d), “… 6(c) and 6(d) are special cases as I said. … Example 4, they will say, Okay, I’m quite comfortable with the method [technique], now these are all the unusual cases …” (Post-Lesson Interview 2, 10:04). The special cases were situations when students usually conclude that there are no solutions to the inequalities because Step 1 results in either no real roots (Example 6(c)) or equal roots (Example 6(d)).

Question 6(c) is a rather unusual question… your first instinct is to try to find x-intercepts, alright? And then you realise that it doesn’t work … Now, if you are doing a quadratic equation, and you use the formula and you see this you say, No solution. … But that’s not the case for this inequality …. (Lesson 6, 21:51).

Through Examples 6(c) and 6(d), he expected his students to modify their technique to solve quadratic inequalities by examining their incorrect conclusion—“no real roots” means no solution to the inequalities—by referring them back to the graphical representation. In other words, Teacher 13’s “advance one more”—in the case of Example 6(c)—meant that the task required students to modify the learnt technique further to accommodate the “no real roots” situation. In particular, the conclusion “no real roots” in Step 1 does not prevent the use of graphical representation in Step 2 to obtain the required solution set for the inequalities.

Similarly, Example 6(d) presented yet another “special case” of “equal roots” which required yet another modification in the way students should use the technique, in this case, the graphical interpretation of 3(x - 5)² ≤ 0. Figure 13.4 gives a brief outline of how Teacher 13 “advance one more” in between examples:

Fig. 13.4

Whiteboard work of Teacher 13 for Example 6(a) to 6(b) to 6(c) to 6(d)

• 6(a) → 6(b): included alternative method to solve equation

• 6(b) → 6(c): no solution in equation does not imply no solution for inequality

• 6(c) → 6(d): graphical representation for “equal roots” case

We noted that there was careful design of Examples 5 and 6. Teacher 13 was not just using examples merely to repeat practice the same procedures; he deliberately used the sequence of examples to “advance one more”. By this, he meant that, where appropriate, the next example provides the technique refinement/modification: “one more” step in the direction of a more comprehensive applicability of the technique to cases where students would normally not consider by themselves. Thus, our first conjecture is that Teacher 13 designed the sequence of his notes in such a way to achieve the design principle: (1) advance the technique.

Conjecture 2: Advance more through reasoning

Our analysis of Teacher 13’s intention through his carefully selected examples in the Notes showed that he wanted his students to see each shift in the solution strategy through the examples and to learn to “think flexibly”.

Alright, there are different ways to actually solve this [writes on board as he speaks]. But ‘cause yesterday’s example [Example 5 & 6(a)] is [to] use quadratic [formula], then you just use quadratic formula, right? Have to be a little bit more flexible than that. (Lesson 6, 11:36)

… if they keep using the same method, it indicates that they are not quite thinking about what they are doing, alright. … So I want to break them out of that mode… (Post-Lesson Interview 2, 14:23)

In particular, from Teacher 13’s interview, we learn that the development of reasoning was intentionally built into the Notes: “we purposely build in a lot of reasoning type of steps for them to do”. Teacher 13 elaborated this during an interview,

… today the focus is on the non-standard examples [step 1 cannot be factorised] … So here is to promote reasoning in general, because here the-the basic idea they want to learn is if I can get the sketch of the graph [Step 2], I can use the graph to deduce a solution, […] This way we make sure that they know the thinking behind the particular graphical method [Step 2], and we put in all these parts to make sure that they are actually applying the reasoning behind the graphical method [Step 2]. (Post-Lesson Interview 2, 22:16)

In other words, “advance one more” was done through reasoning. We observed that for Example 5, in Teacher 13’s Lesson 6, two methods were used to identify the roots of the quadratic expression 2x² + x – 4 = 0 in Step 1. Figure 13.5 shows the two methods, namely, Method 1 (quadratic formula) and Method 2 (complete the square).

Fig. 13.5

Comparing methods in Example 5

He encouraged his students to think and choose the method they prefer. This act was intentional and engineered into the design of the Notes as shared by Teacher 13 during the interview,

So again we give them the options, we don’t tell the students, we try not to tell the students which way to do… This way, both ways are fine for us. So we give them option—you choose the option that you think you prefer, that you think you are more likely to succeed in. So that’s the design principle. (Post-Lesson Interview 2, 11:10)

The comparison of methods was also seen in Fig. 13.4, Example 6(b) and Example 6(c). From Teacher 13’s interview “[Example 6(b)] they [are] used to illustrate that there are other methods [Step 1] we can use.” He expected his students to compare the various methods to find the roots in Step 1 and decide on the easier method (see Figure 13.4). Clearly, the reasoning process of comparing was intentionally built into some of the examples.

In the vignette for Example 6(c) presented in Table 13.2, we unpack two other reasoning processes used by Teacher 13: justifying and inferring for students in Group A during their seatwork.

Table 13.2 Justifying and inferring with students in Group A for Example 6 (c) Lesson 6

In Line 11, Teacher 13 wanted the students in Group A to infer what it meant when there were no x-intercepts. Student 1 claimed that the graph did not touch the x-axis in Line 12. Student 2 inferred and claimed that “x is more than 0” in Line 16. Student 2 made another claim that the graph “is above 0” in Line 18. The engagement with reasoning does not stop here as Teacher 13 required Student 2 to justify her claim, “Is that true?” in Line 23.

Table 13.3 presents another vignette for Example 6(c) where the two reasoning processes, justifying and inferring, were unpacked with another group (Group B) of students.

Table 13.3 Justifying and inferring with students in Group B for Example 6 (c) Lesson 6

Here we noted that Teacher 13’s other design principle is: (2) the technique was advanced through comparing, inferring and justifying. In the next two sections, we present the evidence for the next two uncovered design principles.

Conjecture 3: Expose and target students’ faculty reasoning through carefully designed examples

One of the reasons why Teacher 13 built-in reasoning opportunities through the carefully selected examples in Example 6 was to deal with anticipated students’ misconceptions (e.g., no solution in equation implies no solution for inequality).

… or if there’s a misconception that keeps popping up, I’ll also bring them up. … Just now this question, the one where the solution is all real values [Example 6(c)], so many of them … will say, “Oh, no answer; cannot; no roots, because it’s square root negative 40”, and then they want to stop there. So I have to address that point … (Post-Lesson Interview 2, 15:47)

Revisiting the vignette in Table 13.2, from Line 3, we noticed that Teacher 13 picked up Student 2’s faulty reasoning in Example 6(c). In Line 4–6 he had Student 2 confront the faulty reasoning, and in Line 6–19 Teacher 13 addressed and corrected Student 2’s faulty reasoning. From Table 13.2, we see that Teacher 13 was not merely correcting wrong technique but also the faulty reasoning underlying it. Hence, in the design of his Notes, he incorporated examples where he could expose the faulty reasoning behind the wrong techniques. We therefore state that Teacher 13 utilised a third design principle: (3) special cases to expose and target students’ faulty reasoning undergirding the techniques they used.

Conjecture 4: Presentation of solutions to reflect reasoning

Teacher 13 was concerned about presentations of the written reasoning in a way that is acceptable to the mathematical community and he required the students to present their solutions very clearly. He emphasised to his students that “you have to be very specific in your presentation so people understand what you are doing”. (Lesson 5, 25:59). For example, in Fig. 13.6, Teacher 13 showed his reasoning in arriving at the correct solution on the whiteboard and pointed out the incorrect way of presenting the solution for Example 5.

Fig. 13.6

Formal reasoning in the written form

The working looks almost the same. [writes on board] But this is just so that you make it very clear that, [here, in the italicised text, the teacher is telling the students how they can write their justification] I’m not trying to solve the inequality, here. I’m only considering what happens when it is equals to 0. So that I can draw my graph. So that statement is to justify this set of working. So there’s no confusion. (Lesson 5, 28:49)

Reflecting on our analysis of the first unit of analysis, we noticed that the white board appeared to be central in stringing together all the intended objectives by the teacher as expressed in earlier stated preliminary design principle:

• (4) The whole class instructional segment was used to consolidate and formalise the reasoning in standard written form.

Figure 13.7 presents our provisional diagrammatic representational this stage of our analyses.

Fig. 13.7

An example of technique and reasoning applied within and across Examples 5 and 6

5.2 Analysis of Unit 2: Further Examination of the Conjectures

For Unit 2, the description is deliberately brief as we zoom straight into providing evidence on how the design principles in the previous section are supported or refined. The technique in Unit 2 involves the following steps:

• 1. Obtain the (expected) roots (same as Unit 1)

• 2. Algebraic deduction together with graphs to solve the inequality

5.3 Advance the Technique

Figure 13.8 shows the sequence of examples in this second unit of analysis. The preamble in the Notes shows that Unit 2 was intended to continue to develop students’ techniques in solving quadratic inequalities using “algebraic approach”.

Fig. 13.8

Examples 10, 11 and 12 in the instructional materials

In Step 2, Example 10 (see Fig. 13.8), students “use the algebraic deduction to solve the inequality” by considering two cases for $\left({2x - 3} \right)\left({x - 2} \right) > 0$.

• Case 1: Make logical connections between $\left({2x - 3} \right) > 0$ and $\left({x - 2} \right) > 0$ and with the aid of number line conclude that x > 2.

• Case 2: Make logical connections between $\left({2x - 3} \right) < 0$ and $\left({x - 2} \right) < 0$ and with the aid of number line conclude that x < $\frac{3}{2}$.

Putting the conclusions of the two cases together, x > 2 and x < $\frac{3}{2}$, and with the aid of number line, students solve the inequality $2x^{2} - 7x + 6 > 0$ when x < $\frac{3}{2}$or x > 2. As indicated in the Notes, the inequality stated in Example 10 is identical to Example 1. The cubic expression in Example 11 required the students to extend the method of factorisation (Step 1) into products of linear and quadratic expression

$$x^{3} {-}x^{2} + x{-}{1} = x^{2} \left({x{-}{1}} \right) \, + \, \left({x{-}{1}} \right) \, = \, \left({x{-}{1}} \right)\left({x^{2} + {1}} \right)$$

and subsequently apply a similar argument as Example 10 for Step 2. For Example 12, in Step 1, the numerator 3$x^{2} + 2x - 1$ can be factorised easily into (3x – 1)(x + 1) but the denominator cannot be factorised into linear factors with rational coefficients. Hence, flexibility in thinking in the use of the method is required - completing the square was used instead. For Step 2, applying the algebraic approach, the numerators and denominators of $\frac{{3x^{2} + 2x - 1}}{{4x - x^{2} - 7}}$ need to be considered separately (refinement and development of algebraic method).

• 10 → 11: extend technique to cubic inequalities

• 11 → 12: extend technique to rational inequalities

Examples 10, 11 and 12 thus supports Conjecture 1.

5.4 Advance Technique Through Comparing, Inferring and Justifying

As reflected in the instructions for Example 10 (see Fig. 13.8), the reasoning process of comparing was intentionally built into Example 10 for students to compare and contrast the graphical and the algebraic method. Teacher 13’s video Lesson 8 showed him comparing the two methods (see Fig. 13.9).

Fig. 13.9

Comparing methods in Example 10

We also observed his use of inferring to develop the algebraic method through Example 10 (see Table 13.4).

Table 13.4 Inferring for Example 10 in Lesson 8

It is clear that Teacher 13 had reasoning in mind for Examples 11 and 12:

Yeah so, I brought them to the algebraic reasoning for this, showed them how to obtain a solution and main thrust of the message is that we try not to use this method [Step 2] for basic quadratic inequalities,… But why we are talking about these kind of reasoning is because of certain questions leading to these two [referred to Examples 11 and 12]. So these are considered special cases. So, here… After they factorise one of these factors it’s like, ‘x² + 1’ I think. Ah, so have to guide them through the reasoning of if ‘x² + 1’ is positive, therefore the other factor has to be negative and so on. … (Post-Lesson Interview 3, 05:21)

Examples 11 and 12 were the examples in the Notes that served as vehicles to pull along the development of mathematical reasoning as the technique was advanced.

Inferring was observed during the discussion of Example 11 in Teacher 13’s Lesson 8. For example, during the class seatwork, Teacher 13 led his students to express the cubic expression in Example 11 as $\left({x - 1} \right)(x^{2} + 1)$. Next, he asked “… Then what can you deduce about those two factors?” so that his students can infer the polarity of the two factors for the cubic expression to be non-positive.

Inferring as well as justifying were observed in the discussion of Example 12 in Lesson 8. For example, in Table 13.5, Teacher 13 required his students to justify that 4x−x²−7 (the denominator) is negative. He also required his students to infer how knowing the denominator to be negative for all real values of x contribute to the overall polarity of $\frac{{3x^{2} + 2x - 1}}{{4x - x^{2} - 7}}$.

Table 13.5 Justifying and inferring for Example 12 in Lesson 8

Other incidents of justifying were also observed in Example 12, e.g., as Teacher 13 interacted with a group of students (Group C). Teacher 13 said to the group, “What makes that for sure negative—may not be, right?… must have a stronger argument than that” (Lesson 8, 21:54). And again with students in Group C, “so how do you justify this, no matter what must be negative?” (22:38).

The built-in reasoning features of comparing, justifying and inferring to advance the technique were evident in Examples 10, 11 and 12, thus supporting, Conjecture 2.

5.5 Expose and Target Students’ Faulty Reasoning Through Carefully Designed Examples

During the whole class discussion in Lesson 8, we observed Teacher 13 exposing and addressing students’ faulty reasoning undergirding the technique they used for Example 11, thus supporting Conjecture 3 (see Table 13.6).

Table 13.6 Example 11 in Lesson 8

5.6 Consolidate and Formalise Reasoning in Written Form Through Whole Class Instructional Segment

When the students had difficulty writing the justification for Example 12, Teacher 13 referred students to his written justification on the board at the end of each example—thus, the importance of whole class discussion and Teacher 13’s formal written reasoning on the board work to consolidate and support the development of method and reasoning through the sequence of examples. This supports Conjecture 4. In the last post-lesson interview, Teacher 13 said that “we need to train them how to write, how to justify that x² + 1 was positive [Example 11]” (25:04) and “I try to guide them how to write the justification”. Teacher 13 was also seen to emphasise the importance of communicating written reasoning clearly for Example 12 “and present properly” (Lesson 8, 20:49).

Figure 13.10 summarises the technique and reasoning applied within and across Examples 10, 11 and 12 from our analysis of Unit 2.

Fig. 13.10

An example of technique and reasoning applied within and across Examples 10, 11 & 12

We present the findings of the third unit in summary form in Appendix A. Figure 13.11 summarises the four design principles presented in this paper.

Fig. 13.11

Summary of the four design principles

6 Discussion

As shown in the analyses, the design of practice examples involves a complex interaction among the sequence of practice examples, reasoning and explication of the reasoning in Teacher 13’s lessons. Reasoning was not merely an afterthought or add-on to the sequencing of examples in Teacher 13’s Notes. He arranged his sequence of examples in such a way so that not only the technique of solving inequalities was developed; it was also amenable to reasoning moves supporting each tweak of the technique. He wanted students to reason along the whole trajectory of “twists and turns” from one example to the next. They were intended for students to advance the technique to increase their flexibility and mathematical reasoning as they practised the 2 steps in the technique.

Repeatedly, Teacher 13 mentioned that helping the students to think flexibly was his explicit goal of instruction. By this, he meant that as the students work through the examples, they would learn beyond a direct application of technique. Instead, they were expected to attend to necessary modifications to the technique and thus adapt flexibly through reasoning to suit the change in each proceeding example.

But reasoning was not merely embedded implicitly with the design of the Notes; it was also explicated overtly as an instructional goal for the students during the lessons. When they worked on the examples during seatwork, Teacher 13 repeatedly pressed students to reason out their steps. He drew on students’ “raw reasoning”—including faulty reasoning—as he led whole class discussions following the seatwork to demonstrate sound mathematical reasoning in final written form. In the process of completing the examples, students were expected to develop their ability to attend to alternative solutions and utilise them flexibly in subsequent examples, in accordance to Watson and Mason (2006). Comparison of strategies were also encouraged both within an example and across examples. What came through strongly in the case of Teacher 13 was his use of reasoning as a kind of glue to provide adhesive in these ways:

• 1. Form the undergirding fallback to link the story of technique-tweaking across the examples he designed in his Notes;

• 2. Link the seatwork component of his classroom practice to the whole class discussion segment. In particular, he used students’ raw reasoning attempts during seatwork as ingredients to present (and correct) reasoning in a way that sets the standard of reasoning norms that is acceptable to the community;

• 3. Binds the instructional materials closely with the actual classroom enactment—interaction between task design and pedagogies (Sullivan, Knott, & Yang, 2015).

For Point 3, we noted that it is not uncommon in actual classroom teaching of mathematics to find incoherence between the design of instructional materials and classroom enactment. For example, it is conceivable that the designed instructional materials and classroom enactment are driven by divergent goals so that classroom work goes down a different path from the intended trajectory embedded in the materials. In the case of Teacher 13, as his central focus was on reasoning, both the Notes and the classroom practices are drawn together to build around the central coherence of the reasoning process. The result was a tight materials–classroom link that was strengthened through a heavy emphasis on rigorous reasoning. Evidence of this tight link can be found in almost every “movement” across adjacent pairs of examples (e.g., Example 5 → Example 6(a)). When we combine the insights with the findings (they are also represented in Figs. 13.7, 13.10 and 13.11), we construct a visual depiction of Teacher 13’s design work as shown in Fig. 13.12.

Fig. 13.12

An illustration of technique and reasoning applied across sequence of examples

The centrality of mathematical reasoning in Teacher 13’s plan and action serve as an organising frame to tie the various instructional pieces together. In other words, the model as illustrated in Fig. 13.12 has the potential of depicting teachers’ ways of organising and connecting instructional components that matter to them—in the case of Teacher 13, it demonstrated his organisation around mathematical reasoning. In identifying the “glue” and the key adherents around it, we can begin to characterise teacher’s fundamental instructional methods. A discussion of alternative models—around different glues and adherents—can be a productive way forward in teachers’ inquiry towards quality mathematics teaching.

7 Conclusion

Developing students’ mathematical reasoning is a core aspect of teaching and learning the mathematics classrooms (Ball & Bass, 2003; Boaler, 2010). To promote students’ mathematical reasoning, students need to be provided challenging learning environments instead of lessons where students just solve exercises using well-known procedures (Mata-Pereira & Ponte, 2017). However, suitable tasks are not enough to ensure that students develop mathematical reasoning (Ball & Bass, 2003). It can thus be challenging to design tasks that place reasoning as its ostensible goal where the task must be just right to ensure that students develop reasoning. It is therefore, important to know the explicit task design moves which lead students to engage and advance in mathematical reasoning, and in what ways they may be used in the classroom. Teacher 13’s case places reasoning as the centre piece (Fig. 13.12), as such, it illuminates how sequences of practice examples could be designed and enacted through careful and informed decisions to develop and advance students’ reasoning. This paper, therefore, can provide the mathematics education research community another perspective at designing tasks.

Appendix A

Third Unit of Analysis