Keywords

Introduction

Nowadays, flexible AC transmission systems (FACTS) have found an extensive application in the power transmission system. With the advancement in power electronics-based controller technology, the FACTS controller damped system oscillation by improving stability [1, 2]. Among the FACTS devices static VAR compensator (SVC) [3, 4] has popular for its instantaneous response to voltage change. The thyristor controlled series capacitor (TCSC) [5, 6] of the FACTS family damped electromechanical oscillations, regulate transmission voltage, limit short circuit currents and mitigate the power system oscillation. The second-generation FACTS device static synchronous compensator (STATCOM) has quicker response compare to conventional SVC to system abnormality. The STATCOM controls the reactive power flow in the transmission line [7,8,9]. The SSSC is a second-order FACTS device that has several advantages among other FACTS devices due to its storage element [10, 11]. Most of these devices utilize IGBT and GTOs based voltage source converter (VSC). The SSSC controller directly controls the current flow in the transmission line by regulating the reactive power requirement of the power system. This controller does not change the transmission line impedance like TCSC controller, hence does not suffer from resonance issue [12,13,14,15].

In previous literature, several population based optimization algorithm (POA) have been adopted to estimate the controller parameter for the optimal operation of the controller. In [16] a comparative study is carried out between GA and PSO based SSSC controller parameter design. Even though GA can effectively find the global optimal result but takes a very long run time. The PSO suffers from slow convergence with weak local search ability [17]. In [18], the bacteria forging (BF) algorithm has been addressed for power system stability controller design. The main disadvantage in the BF algorithm that it searches the global solution in random directions which may cause long run time. Various new algorithms have been adopted recently for the design of an SSSC controller in recent times like whale optimization algorithm (WOA) [19, 20], modified WOA [21] and hybrid DE-PSO [22] etc.

SCA is a newly developed optimization algorithm which uses sine/cosine functions during algorithm formulation [23]. This approach efficiently transfers from the exploration phase to the exploitation phase by using sine/cosine functions. However, the optimization algorithm suffers from slow convergences and the consequences due to unbalanced distribution among the exploration and exploitation phase. So, the conventional SCA algorithm fails to achieve the solution with better convergence. In this paper FO PD structured SSSC controller is designed using modified SCA (MSCA) algorithm which can overcome the discussed issues of conventional SCA.

The following objectives are carried out in this present study.

  1. 1.

    This chapter primarily focuses on the modeling of an SSSC controller with FO PD damping.

  2. 2.

    The proposed controller provides extra freedom in controller tuning.

  3. 3.

    Finally, for optimum tuning of the FO PD parameters of the SSSC controller, MSCA is applied.

SCA and Its Modification

Sine Cosine Algorithm is a POA first proposed in [23], which uses sine/cosine function in the algorithm to update the position. Generally, POA starts with a randomly selected solution set. Then the iterative process evaluates the selected solution set in formulated objective function with certain system constraints to obtain the global solution. Hence a sufficient number of the solution set with more number of iteration increase the probability of getting an optimal solution. The optimization process in the SCA algorithm progresses its search for an optimal solution in exploitation and exploration phases. The SCA algorithm search for a promising region in the search space in the exploration phase and gradually changes the value of random solutions in exploitation phase to get an optimal solution. During both phases, the position updating formulation is presented below.

$$\begin{aligned} X_j^{n+1} = {\left\{ \begin{array}{ll} X_j^n+r_1 \times \sin (r_2)\times \mid (r_3 \times pos_j^n)-X_j^n\mid &{} r_4<0.5\\ X_j^n+r_1 \times \sin (r_2)\times \mid (r_3 \times pos_j^n)-X_{jj}^n\mid &{} r_4 \ge 0.5 \end{array}\right. } \end{aligned}$$
(1)

In (1) \(X_j^n\) represents jth-dimension current solution after nth-iteration. The term \(pos_j\) defines the destination point position in jth dimension. The random variables in (1) are the main parameters of the SCA algorithm whose values ranges in between [0, 1]. The random parameter \(r_1\) decides the direction of the next position either inside the solution and destination or away from it. \(r_2\) decides the distance travel during movement in the direction of the destination or far away from the destination. As shown in (1), \(r_3\) add weight to the position \(pos_j\) to emphasize or de-emphasize impact of the destination in order to define the distance. Whenever \(r_3 > 1\) SCA gives emphasis to the effect of destination and for \(r_3 < 1\) SCA does not give emphasis to the effect of destination. Finally, \(r_4\) value decides the sine or cosine function be selected to update the position as given in (1).

Fig. 11.1
figure 1

Process flow chart of the MSCA

Full size image

To converge towards the global solution, the optimization algorithm should able to find a promising region in the search space. To achieve this objective, the optimization algorithm should maintain a proper equilibrium among the phase of exploration and exploitation. To maintain equilibrium between these two phases, the SCA estimate the range of sine and cosine in (1) by changing the value of adaptively as given below:

$$\begin{aligned} r_1=a-n\left( \frac{a}{N}\right) \end{aligned}$$
(2)

where n define the current state of iteration with N being the maximum number of iteration. The variable a is a constant maintain equilibrium between two phases. By linearly increasing the \(r_1\) with respect to the iteration count, the number of iteration needed is high which increases the algorithm’s computation time. Furthermore, the convergence rate also decreases. This paper presents modified SCA (MSCA) by varying \(r_1\) as given in (3) to boost the convergence and get the optimal global solution.

$$\begin{aligned} r_1=a-n^{1.5}\left( \frac{a}{N^{1.5}}\right) \end{aligned}$$
(3)

The constant a in (3) is set to be 1.6 and the value \(r_1\) is varying non-linearly with the iteration count as in (3) to attain the optimal solution with high convergence. Here, the iteration n is changed to its fractional power of 1.5, the maximum number of iteration N is changed to its fractional power value of 1.5. The comprehensive process flow chart MSCA presented in Fig. 11.1.

System Modeling and Controller Design

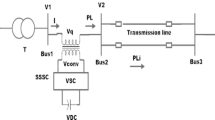
SSSC Based System Modeling

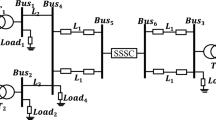
It is necessary to evaluate the performance of any damping controller based upon SSSC along with their proper design. Therefore, a SMIB system is being considered as shown in Fig. 11.2, comprising of a synchronous generator that is linked to an infinite-bus with the help of a transformer and an SSSC.

Fig. 11.2
figure 2

SMIB system with FACTS controller

Full size image

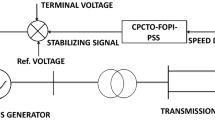
The Proposed Controller

Recently, the key emphasis is to update the traditional PID controllers using the Fractional Calculus initiative. A thorough explanation of the FO PD type controller is elaborated in [21]. The designed controller in this chapter consisted of FO PD structured lead-lag components as given in Fig. 11.3. The FO PD type design consists of a fractional integrator, proportional gain, derivative gain and a filter. The lead-lag structure components are discussed in [21].

Fig. 11.3
figure 3

Controller structure of FO PD type SSSC

Full size image

Problem Formulation

In this chapter, First order derivative filter \(K =100\) [21] and \(t_{WS}\) = 10 s is used. \(K_{PS}\), \(K_{DS}\) are the gains of the controller, \(\lambda _S\) is the fractional integrator and the time constants to be measured. For the damping of the power system oscillations, the voltage of the injected series is balanced, and the effective \(V_q\) is given by:

$$\begin{aligned} V_q = V_{qref}+\Delta V_{q1} \end{aligned}$$
(4)

To achieve improved device performance, the MSCA is used to adjust the controller parameters. Objective function description is a first stage prerequisite for controller purposes using the latest heuristic optimizations. The objective function for the speed deviation for the SMIB system is expressed in (5).

$$\begin{aligned} J= \int \limits _{0}^{t} \mid \Delta \omega \mid t dt \end{aligned}$$
(5)

where, t is the range of simulation time is the change is speed. The performance indices named ITAE are selected as an objective function to be minimized. However, Minimizing objective function J is subject to controller parameter restriction.

$$\begin{aligned} {\text {Minimize}} J \end{aligned}$$
(6)

Subject to

$$\begin{aligned} \begin{aligned} K_{PS}^{\text {Min}} \le K_{PS} \le K_{PS}^{\text {Max}} \qquad K_{DS}^{\text {Min}} \le K_{DS} \le K_{DS}^{\text {Max}}\\ \lambda _S^{\text {Min}} \le \lambda _S \le \lambda _S^{\text {Max}} \qquad t_{1S}^{\text {Min}} \le t_{1S} \le t_{1S}^{\text {Max}}\\ t_{2S}^{\text {Min}} \le t_{2S} \le t_{2S}^{\text {Max}} \qquad t_{3S}^{\text {Min}} \le t_{3S} \le t_{3S}^{\text {Max}}\\ t_{4S}^{\text {Min}} \le t_{4S} \le t_{4S}^{\text {Max}}\\ \end{aligned} \end{aligned}$$
(7)

It is to be noted that two gains, one fractional integrator and four time constant parameters are needed to be optimized for a SMIB system.

Result and Analysis

A toolbox called Sim Power Systems (SPS) has been used exclusively for all the simulations and designing of the damping controller. Engineers are capable of simulating these Power Systems using the MATLAB-based design tool SPS that helps them design and build models with ease.

Application to SMIB System

For the implementation and efficient performance of the MSCA algorithm, the selection of various parameter values has to be done carefully. The various cases selected are as follows.

Case A: Nominal Loading Condition

In this case, the suggested controller performance is demonstrated at \(P_e\) = 0.8 p.u loading conditions for nominal loading with respect to the occurrence of a severe disturbance in the system. At time t = 1s, a 3-cycles, 3-phase fault is applied at the mid-section of the transmission line. Figures 11.4, 11.5, 11.6 and 11.7 depicts the various responses of the system which leads to the conclusion that the MSCA optimized proposed controller gives improved dynamic response as compared with PSO, GA and original SCA optimized proposed controller.

Fig. 11.4
figure 4

Nominal loading speed deviation response

Full size image
Fig. 11.5
figure 5

Power angle response

Full size image
Fig. 11.6
figure 6

Nominal loading tie-line power

Full size image
Fig. 11.7
figure 7

SSSC injected voltage

Full size image

Case B: Light Loading Condition

To look at the superiority of the planned SSSC controller, its performance is evaluated under light load condition. In this case,\(P_e\) = 0.55 p.u is set for the generator load and a 100 ms 3-phase fault is applied close to bus-3 at t = 1 s. The system response under this possibility which explains the efficacy of the suggested SSSC controller under different working conditions and sort of disruption has appeared in Fig. 11.8. Also, the proposed MSCA method provides enhanced transient response with PSO, GA and original SCA optimized proposed controller.

Fig. 11.8
figure 8

Light loading speed deviation response

Full size image
Fig. 11.9
figure 9

Heavy loading speed deviation response

Full size image

Case C: Heavy Loading Condition

The performance of the suggested SSSC controller is also tested by generator heavy loading i.e., \(P_e\) = 1.0 p.u. In this case at t = 1 s, at the midpoint of the transmission line near bus 4, a 100 ms 3-phase fault is applied. The speed deviation responses are tested in heavy loading condition is displayed in Fig. 11.9. Figure 11.9 shows the MSCA optimized SSSC controller gives more stable performance contrast with PSO, GA and SCA optimized controller.

The optimized parameters of the suggested controller are presented in Table 11.1 for the SMIB system. Table 11.2 shows that the least ITAE values are observed with MSCA methods that take into account different instances compared to PSO, GA and SCA methods.

Table 11.1 PSO, GA, SCA, and MSCA optimized FO PD type SSSC controller parameters
Full size table
Table 11.2 SMIB system ITAE values considering PSO, GA, SCA and MSCA techniques
Full size table

To improve stability, the existing work can be applied to an integrated power system by means of a wind farm [24].

Conclusions

In this present work, a modified SCA tuned FO PD based SSSC controller is designed to improve power system stability. For the suggested controller design issue, a time-domain objective function is used to reduce the oscillations of the power system. In addition, modified SCA is used to tune the FO PD type FACTS controller. The efficacy of the controller configuration is determined by the use of the SMIB system under different serious disturbances. To reveal the effectiveness of the proposed system, the results of the proposed modified SCA tuned FO PD type SSSC structure are compared with the PSO, GA and original SCA.