Keywords

1 Introduction

Nowadays, with the rapid development of science and technology, human society has stepped into the era of the integration of realistic space and cyberspace. The information superhighway has become the basis of economic development. Thus, how to effectively ensure the security of information is of extreme significance.

Classical cryptography is an important tool to ensure the information security. Unfortunately, quantum algorithms cause them to be broken through in polynomial time. Thereupon, quantum cryptography, which is proven to be unconditionally secure over an insecure channel, has attracted more and more attention from both industry and academia. As a result, so far all kinds of quantum secure communication protocols have been proposed by the researchers such as quantum key distribution (QKD) [1,2,3,4,5], quantum secure direct communication (QSDC) [6,7,8], quantum teleportation (QT) [9, 10], remote state preparation (RSP) [11, 12], quantum signature (QS) [13, 14], quantum private query (QPQ) [15, 16], quantum private comparison [17] and so on.

Quantum secret sharing (QSS) is a significant branch of quantum secure communication, which is deemed to be the quantum counterpart of classical secret sharing. In fact, QSS combines quantum mechanics and the kernel idea contained in classical secret sharing to split either a classical secret (bit string) or a quantum state (unknown quantum state) into several shadows, a specific quantity of shadows can reconstruct the secret but every shadow alone cannot. The quantum secret sharing schemes were firstly proposed by Hillery et al. and Karlsson et al. at the same year [18, 19]. Since then, a great many of QSS schemes have been put forward by experts and scholars in both theory and experiment.

In 2008, Deng et al. presented an efficient high-capacity QSS protocol based on the ideas of quantum dense coding [20]. In 2010, Gu et al. proposed two robust three-party QSS protocols to be against both collective-dephasing noise and collective rotation noise with logical Bell states [21]. In 2012, Yang et al. not only summarized how to construct a verifiable quantum (k, n) threshold protocol, but also designed a specific scheme by means of Lagrange Interpolation formula and post-verification mechanisms [22]. In 2013, Hsu et al. put forward a dynamic QSS protocol with the entanglement swapping of EPR pairs to deal with the volatility of agents [23]. In 2015, Rahaman et al. elaborately devised the first QSS scheme by utilizing the local distinguishability of orthogonal multipartite entangled states [24]. In 2017, Wang et al. designed a multi-layer QSS protocol based on GHZ state and generalized Bell-basis measurement [25]. In the same year, Chen et al. came up with a QSS scheme using the Borras-Plastino-Batle (BPB) state, in which the module division and coupling of quantum communication protocols was investigated [26]. In addition, Wang et al. attempted to make use of the local distinguishability of orthogonal Dicke states and multi-qudit entangled states to construct the QSS schemes, respectively [27, 28]. In 2019, a new multi-party QSS model was built by Zhang et al. by analyzing the property of multi-qubit entangled states [29]. In the same year, a novel rational non-hierarchical quantum secret sharing protocol emerged, which is widely applicable [30].

It is easy to discover that each of aforementioned QSS schemes is deem to be a representative of one kind of QSS. Aiming at the fact that it is difficult to prepare multi-particle entangled states, based on layered structure, we put forward a multi-layer QSS protocol with five-particle GHZ states which can be created in laboratory. In our scheme, the secret, carried by one quantum state, is distributed to the multiple agent nodes in the network layer by layer from root to layered agents. Only if all agents at the last layer cooperate together, the secret can be reconstructed.

The structure of this paper is organized as follows. In Sect. 2, we come up with a multi-layer quantum secret sharing protocol by means of five-particle GHZ states. In Sect. 3, we design two iterative algorithms under the guidance of computational thinking. One is to calculate the multi-qubit entangled states carrying the secret in the last layer, while the other is to compute the recovery operations performed by the designated agent in the last layer. Finally, this paper ends up with a discussion in Sect. 4.

2 Multi-layer Quantum Secret Sharing Protocols

In this section, we design a multi-layer QSS protocol with five-particle GHZ states by using Bell-basis measurement. We take into account that the agent’s number in each layer is a geometric sequence with common ratio 4. The workflow of this QSS protocol can be depicted as follows.

2.1 The Secret Sharing Process of the First Layer

Suppose that there are five participants, one sender Alice and four agents \( {\text{Bob}}_{\text{i}} \left( {{\text{i }} = 1, \cdots , 4} \right) \) in the first layer. Alice holds a secret carried by the one-qubit quantum state and wants to distribute this secret to the agents \( {\text{Bob}}_{\text{i}} \left( {{\text{i }} = 1, \cdots , 4} \right) \). The one-qubit state corresponding to this secret can be written as.

$$ \left|\uppsi \right._{1} \rangle =\upalpha\left| 0 \right.\rangle +\upbeta\left| 1 \right.\rangle , $$
(1)

where \( \upalpha \) and \( \upbeta \) are complex numbers, which satisfy the normalization condition \( \upalpha^{2} +\upbeta^{2} = 1. \)

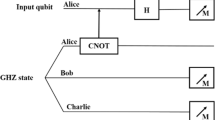
For sharing the one-qubit state with four agents, Alice first prepares a five-particle GHZ state, as shown in the Fig. 1(a), which can be expressed in

Fig. 1.
figure 1

The secret sharing process of the first layer

Full size image
$$ \left|\uppsi \right.\rangle_{{1^{\prime}2345}} = \frac{1}{\sqrt 2 }\left( {\left| {00000} \right.\rangle + \left| {11111} \right.\rangle } \right) $$
(2)

This five-particle GHZ state can be created in laboratory conditions. To set up the quantum channel, Alice sends the particle 2 to \( {\text{Bob}}_{1} \), the particle 3 to \( {\text{Bob}}_{2} \), the particle 4 to \( {\text{Bob}}_{3} \) and the particle 5 to \( {\text{Bob}}_{4} \). Therefore, the state of the whole six-particle system can be described as

$$ \begin{aligned} \left|\uppsi \right.\rangle_{1} \otimes \left|\uppsi \right.\rangle_{{1^{\prime}2345}} = & \frac{1}{\sqrt 2 }\left( {\upalpha |000000} \right.\rangle +\upalpha\left| {011111} \right.\rangle +\upbeta\left| {100000} \right.\rangle \\ & + \,\upbeta|111111\rangle ) \\ \end{aligned} $$
(3)

In order to transfer the secret to four agents, Alice performs a Bell-basis measurement on the particles 1 and 2 as depicted in the Fig. 1(b). This measurement basis is made up of four Bell states

$$ \begin{aligned} \left| {{\upvarphi }_{1} } \right.\rangle = \frac{1}{\sqrt 2 }\left( {\left| {00\rangle + } \right|11\rangle } \right),\left| {{\upvarphi}_{2} } \right.\rangle = \frac{1}{\sqrt 2 }\left( {\left| {00\rangle - } \right|11\rangle } \right) \hfill \\ \left| {{\upvarphi}_{3} } \right.\rangle = \frac{1}{\sqrt 2 }\left( {\left| {01\rangle + } \right|10\rangle } \right),\left| {{\upvarphi}_{4} } \right.\rangle = \frac{1}{\sqrt 2 }\left( {\left| {01\rangle - } \right|10\rangle } \right) \hfill \\ \end{aligned} $$
(4)

As a result, the state of the whole quantum system, which is composed of six particles, can be rewritten as

$$ \begin{aligned} \left|\uppsi \right.\rangle_{{11^{'} 2345}} = & \frac{1}{\sqrt 2 }[\left| {{\upvarphi}_{1} } \right.\rangle_{{11^{'} }} \left( {\upalpha\left| {0000\rangle +\upbeta} \right|1111\rangle } \right)_{2345} \\ & + \,\left| {{\upvarphi}_{2} } \right.\rangle_{{11^{'} }} \left( {\upalpha\left| {0000\rangle -\upbeta} \right|1111\rangle } \right)_{2345} \\ & + \,|{\upvarphi}_{3} \rangle_{{11^{'} }} \left( {\upalpha\left| {1111\rangle +\upbeta} \right|0000\rangle } \right)_{2345} \\ & + \,|{\upvarphi}_{4} \rangle_{{11^{'} }} \left( {\upalpha\left| {1111\rangle -\upbeta} \right|0000\rangle } \right)_{2345} ] \\ \end{aligned} $$
(5)

It is obvious that the whole system will collapse to a term of Eq. (5) with the probability of 1/4, after Alice implements the Bell-basis measurement.

That is to say, as shown in the Fig. 1(c), the secret carried by the particle 1 is transferred to the quantum system composed of four particles 2, 3, 4 and 5. As a result, this secret is shared by four agents \( {\text{Bob}}_{1} \), \( {\text{Bob}}_{2} \), \( {\text{Bob}}_{3} \) and \( {\text{Bob}}_{4} \) through one time distribution. Only if these four agents collaborate with each other, they can recover the secret.

If Alice decides that the protocol only works in the first layer, she will announce her measurement results and designate one agent to recover the secret at random. Assume she empowers \( {\text{Bob}}_{1} \) to recover the secret, \( {\text{Bob}}_{2} \), \( {\text{Bob}}_{3} \) and \( {\text{Bob}}_{4} \) should carry out a single-qubit measurement in the basis \( |{\text{X}}^{ \pm } \rangle = \frac{1}{\sqrt 2 }\left( {\left| {0\rangle \pm } \right|1\rangle } \right) \) on their own particles respectively and publish their measurement outcomes to \( {\text{Bob}}_{1} \) via a classical channel. According to the measurement outcomes from both Alice and \( {\text{Bob}}_{2} \)–\( {\text{Bob}}_{4} \), \( {\text{Bob}}_{1} \) can recover the original secret by applying a suitable unitary transformation on his particle 2. As illuminated in Table 1, when Alice’s measurement result is \( |{\upvarphi}_{1} \rangle \), \( {\text{Bob}}_{1} \) should carry out the corresponding unitary transformations.

Table 1. Corresponding relationship between the measurement outcomes of \( {\text{Bob}}_{2} \)–\( {\text{Bob}}_{4} \) and the unitary operations performed by \( {\text{Bob}}_{1} \)
Full size table

If Alice wishes to make more agents share this secret, she does not publish her measurement results and not designate any agent to reconstruct it. \( {\text{Bob}}_{1} \), \( {\text{Bob}}_{2} \), \( {\text{Bob}}_{3} \) and \( {\text{Bob}}_{4} \) will continue to distribute this secret to the second layer. Obviously, these four agents are not able to recover the secret accurately, because they are ignorant of Alice’s measurement results.

2.2 The Secret Sharing Process of the Second Layer

After the first distribution, the entangled state, carrying the secret, shared among \( {\text{Bob}}_{1} \), \( {\text{Bob}}_{2} \), \( {\text{Bob}}_{3} \) and \( {\text{Bob}}_{4} \) can be written as Eq. (5). The target is to share this secret among sixteen agents \( {\text{Charlie}}_{\text{i}} \left( {{\text{i }} = 1, \cdots , 16} \right) \) in the second layer.

As shown in the Fig. 2(a), \( {\text{Bob}}_{1} \)–\( {\text{Bob}}_{4} \) should prepare a five-particle GHZ state respectively,

Fig. 2.
figure 2

The secret sharing process of the second layer

Full size image
$$ \begin{aligned} & \quad \;\left|\uppsi \right.\rangle_{{2^{\prime}6789}} = \frac{1}{\sqrt 2 }\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{2^{\prime}6789}} \\ & |\uppsi\rangle_{{3^{\prime}10111213}} = \frac{1}{\sqrt 2 }\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{3^{\prime}10111213}} \\ & |\uppsi\rangle_{{4^{\prime}14151617}} = \frac{1}{\sqrt 2 }\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{4^{\prime}14151617}} \\ & |\uppsi\rangle_{{5^{\prime}18192021}} = \frac{1}{\sqrt 2 }\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{5^{\prime}18192021}} \\ \end{aligned} $$
(6)

For simplicity, the numbers 6, 7, 8, 9 are written as 6–9, the numbers 10, 11, 12, 13 are written as 10–13, the numbers 14, 15, 16, 17 are written as 14–17, and the numbers 18, 19, 20, 21 are written as 18–21.

\( {\text{Bob}}_{1} \) respectively sends the particles 6–9 to \( {\text{Charlie}}_{1} \)–\( {\text{Charlie}}_{4} \) with the help of decoy photons, \( {\text{Bob}}_{2} \) respectively sends the particles 10–13 to \( {\text{Charlie}}_{5} \)–\( {\text{Charlie}}_{8} \) with the help of decoy photons, \( {\text{Bob}}_{3} \) respectively sends the particles 14–17 to \( {\text{Charlie}}_{9} \)–\( {\text{Charlie}}_{12} \) with the help of decoy photons, and \( {\text{Bob}}_{4} \) respectively sends the particles 18–21 to \( {\text{Charlie}}_{13} \)–\( {\text{Charlie}}_{16} \) with the help of decoy photons.

Suppose Alice’s measurement result is \( |{\upvarphi}_{2} \rangle \), the state of the whole quantum system, which is composed of twenty-four particles, can be described as

$$ \begin{aligned} \left| {\uppsi\rangle } \right. & = \left|\uppsi \right.\rangle_{2345} \otimes \left|\uppsi \right.\rangle_{{2^{\prime}6 - 9}} \otimes \left|\uppsi \right.\rangle_{{3^{\prime}10 - 13}} \otimes \left|\uppsi \right.\rangle_{{4^{\prime}14 - 17}} \otimes \left|\uppsi \right.\rangle_{{5^{\prime}18 - 21}} \\ & = \frac{1}{4}\left( {\upalpha\left| {0000\rangle -\upbeta} \right|1111\rangle } \right)_{2345} \otimes \left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{2^{\prime}6 - 9}} \\ & \quad \otimes \left( {\left| {00000} \right\rangle + \left| {11111} \right\rangle } \right)_{{3^{\prime}10 - 13}} \otimes \left( {\left| {00000} \right\rangle + \left| {11111} \right\rangle } \right)_{{4^{\prime}14 - 17}} \\ & \quad \otimes \left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{5^{\prime}18 - 21}} \\ \end{aligned} $$
(7)

After \( {\text{Bob}}_{1} \) completes his measurement work, the state of the whole quantum system will collapse into

$$ \begin{aligned} |\uppsi\rangle = & \frac{1}{4\sqrt 2 }[\left| {{\upvarphi}_{1} } \right.\rangle_{{22^{\prime}}} \left( {\upalpha\left| {0000000\rangle -\upbeta} \right|1111111\rangle } \right)_{3 - 9} \\ & + \,\left| {{\upvarphi}_{2} } \right.\rangle_{{22^{\prime}}} \left( {\upalpha\left| {0000000\rangle +\upbeta} \right|1111111\rangle } \right)_{3 - 9} \\ & + \,|{\upvarphi}_{3} \rangle_{{22^{\prime}}} \left( { -\upbeta\left| {1111000\rangle +\upalpha} \right|0000111\rangle } \right)_{3 - 9} \\ & + \,|{\upvarphi}_{4} \rangle_{{22^{\prime}}} \left( {\upbeta\left| {1111000\rangle +\upalpha} \right|0000111\rangle } \right)_{3 - 9} ] \\ & \otimes \,\left( {\left| {00000} \right\rangle + \left| {11111} \right\rangle } \right)_{{3^{\prime}10 - 13}} \otimes \left( {\left| {00000} \right\rangle + \left| {11111} \right\rangle } \right)_{{4^{\prime}14 - 17}} \\ & \otimes \,\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{5^{\prime}18 - 21}} \\ \end{aligned} $$
(8)

Assume \( {\text{Bob}}_{1} \)’s measurement result is \( |{\upvarphi}_{1} \rangle \), after \( {\text{Bob}}_{2} \) implements a Bell-basis measurement on particles 3 and 3\( ' \), the state of the whole quantum system can be written as

$$ \begin{aligned} |\uppsi\rangle = & \frac{1}{8}[\left| {{\upvarphi}_{1} } \right.\rangle_{{33^{\prime}}} \left( {\upalpha\left| {0000000000} \right\rangle -\upbeta\left| {1111111111} \right\rangle } \right)_{4 - 13} \\ & + \,\left| {{\upvarphi}_{2} } \right.\rangle_{{33^{\prime}}} \left( {\upalpha\left| {0000000000\rangle +\upbeta} \right|1111111111\rangle } \right)_{4 - 13} \\ & + \,\left| {{\upvarphi}_{3} } \right.\rangle_{{33^{\prime}}} \left( { -\upbeta\left| {1111110000\rangle +\upalpha} \right|0000001111\rangle } \right)_{4 - 13} \\ & + \,\left| {{\upvarphi}_{4} } \right.\rangle_{{33^{\prime}}} \left( {\upbeta\left| {1111110000\rangle +\upalpha} \right|0000001111\rangle } \right)_{4 - 13} ] \\ & \otimes \,\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{4^{\prime}14 - 17}} \otimes \left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{5^{\prime}18 - 21}} \\ \end{aligned} $$
(9)

Assume \( {\text{Bob}}_{2} \)’s measurement result is \( |{\upvarphi}_{1} \rangle \), after \( {\text{Bob}}_{3} \) carries out a Bell-basis measurement on particles 4 and 4′, the state of the whole quantum system can be expressed as

$$ \begin{aligned} |\uppsi\rangle = & \frac{1}{8\sqrt 2 }[\left| {{\upvarphi}_{1} } \right.\rangle_{{44^{\prime}}} \left( {\upalpha\left| {0000000000000\rangle -\upbeta} \right|1111111111111\rangle } \right)_{5 - 17} \\ & + \,\left| {{\upvarphi}_{2} } \right.\rangle_{{44^{\prime}}} \left( {\upalpha\left| {0000000000000\rangle +\upbeta} \right|1111111111111\rangle } \right)_{5 - 17} \\ & + \,\left| {{\upvarphi}_{3} } \right.\rangle_{{44^{\prime}}} \left( { -\upbeta\left| {1111111110000\rangle +\upalpha} \right|0000000001111\rangle } \right)_{5 - 17} \\ & + \,\left| {{\upvarphi}_{4} } \right.\rangle_{{44^{\prime}}} \left( {\upbeta\left| {1111111110000\rangle +\upalpha} \right|0000000001111\rangle } \right)_{5 - 17} ] \\ & \otimes \,\left( {\left| {00000\rangle + } \right|11111\rangle } \right)_{{5^{\prime}18 - 21}} \\ \end{aligned} $$
(10)

Assume \( {\text{Bob}}_{3} \)’s measurement result is \( |{\upvarphi}_{1} \rangle \), after \( {\text{Bob}}_{4} \) executes a Bell-basis measurement on particles 5 and 5′, the state of the whole quantum system can be depicted as

$$ \begin{aligned} |\uppsi\rangle = & \frac{1}{16}[\left| {{\upvarphi}_{1} } \right.\rangle_{{55^{\prime}}} \left( {\upalpha |0000000000000000} \right. -\upbeta|1111111111111111\rangle )_{6 - 21} \\ & + \,\left| {{\upvarphi}_{2} } \right.\rangle_{{55^{\prime}}} \left( {\upalpha\left| {0000000000000000\rangle +\upbeta} \right|1111111111111111\rangle } \right)_{6 - 21} \\ & + \,\left| {{\upvarphi}_{3} } \right.\rangle_{{55^{\prime}}} \left( { -\upbeta\left| {1111111111110000\rangle +\upalpha} \right|0000000000001111\rangle } \right)_{6 - 21} \\ & + \,\left| {{\upvarphi}_{4} } \right.\rangle_{{55^{\prime}}} \left( {\upbeta\left| {1111111111110000\rangle +\upalpha} \right|0000000000001111\rangle } \right)_{6 - 21} \\ \end{aligned} $$
(11)

If Alice empowers \( {\text{Charlie}}_{1} \) to recover the secret, she will announce her measurement results. \( {\text{Charlie}}_{\text{i}} \left( {{\text{i}} = 2, \cdots ,16} \right) \) should respectively carry out a single-qubit measurement in the basis \( |{\text{X}}^{ \pm } \rangle = \frac{1}{\sqrt 2 }\left( {\left| {0\rangle \pm } \right|1\rangle } \right) \) on their own particles and publish their measurement outcomes to \( {\text{Charlie}}_{1} \) via classical channels. In the light of the measurement outcomes from \( {\text{Charlie}}_{\text{i}} \left( {{\text{i}} = 2, \cdots ,16} \right) \), \( {\text{Charlie}}_{1} \) can recover the original secret by applying a corresponding unitary transformation on his particle 6.

If Alice wishes to make more agents share this secret, she does not publish her measurement results and not designate any agent to reconstruct it. \( {\text{Charlie}}_{\text{i}} \left( {{\text{i}} = 2, \cdots ,16} \right) \) will continue to distribute the secret to the third layer. To be apparent, \( {\text{Charlie}}_{i} \) cannot recover the secret accurately, since they are unaware of Alice’s measurement results.

2.3 The Secret Sharing of Higher Layer

As shown in Fig. 3, we can achieve the secret sharing of higher layer in the same way described in Subsect. 2.2. Take the third layer as an example, \( {\text{Charlie}}_{\text{i}} \) needs to prepare one five-particle maximally entangled GHZ states, sends four particles to four agents in the fourth layer with the help of decoy photons, leaves one particle in her own hand, and performs a Bell-basis measurements on two particles in her own hands. Finally, the secret can be shared with \( 4^{3} \) agents in the third layer. Repeat this work again and again, we are able to realize that the number of each layer of agents is a geometric sequence with common ratio 4. With the increase of layer number, the secret can be shared with more and more agents. It is worth noting that no matter how many agents the secret is shared with, our proposed protocol only needs five-particle GHZ states.

Fig. 3.
figure 3

The secret sharing process of higher layer

Full size image

3 Iterative Algorithms

In this section, we make every endeavor to look for an appropriate manner to clearly exhibit the whole evolution process of multi-layer quantum secret sharing protocols. The core work is how to calculate the collapsed states and recovery operations quickly and accurately. In view of the fact, we design two iterative algorithms to quickly calculate the collapsed states as well as recovery operations. Algorithm 1 is helpful to quickly calculate the final collapsed states in each layer, while Algorithm 2 is capable of obtaining the specific recovery operation performed by the designated agent in the last layer.

3.1 Algorithm 1

figure a

Before describing this algorithm, we needs to do some preparation work. To be specific, we must create a reference table called Table 2 in accordance with Eq. (5), which plays an important role during calculation. Table 2 presents the corresponding relationship between measurement results and collapsed states in the first layer, it will be called to calculate the collapsed states in next layers. Table 2 is described as follows.

Table 2. Corresponding relationship between Alice’s measurement results and the collapsed states in \( {\text{Bob}}_{1} \)–\( {\text{Bob}}_{4} \)’s hands in the first layer
Full size table

3.2 Algorithm 2

In the last layer, the secret from Alice must be carried by the multi-particle entangled states. The function of Algorithm 2 is able to help the researchers to effectively acquire the recovery operations. For simplicity, in the following algorithm we assume Alice empowers the first agent in the last layer to recover the secret.

figure b

4 Conclusion

This paper puts forward a multi-layer QSS protocol based on five-particle GHZ stats by adopting the layered construction. The number of each layer of agents is a geometric sequence with common ratio 4. There exist two bright spots in this paper. The first bright spot is that sharing the quantum secret in multi-party agents only needs GHZ states with less particles which can be easily prepared in the laboratory. The second bright spot is that we design two iterative algorithms for quickly calculating the collapsed states and recovery operations. The ideas of these two algorithms can make a variety of entangled states to be utilized to design multi-layer QSS protocols and wireless communication protocols.