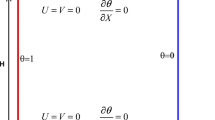Abstract
This work describes the analysis being carried out to find out the diffusion of heat and mass because of multiple sources of heat placed in the medium. A small heating strip is placed centrally apart from regular heating at the left surface. The height of the strip is varied to understand its effect on double diffusion in the medium. The mass diffusion occurs between the vertical surfaces of the cavity under the influence of concentration gradient as well as the thermal gradient. Finite element method (FEM) has been employed for solving the equations. Solution is obtained through an in-house code that works on FEM. The elements of the domain are selected such that they have triangular shape with three nodes. Solution of the equations is obtained following an iterative process, and the results are described using contour plots of concentration, isotherms, and streamlines.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Most of the engineering and scientific problems cannot be experimentally determined due to various restrictions imposed. Among those restrictions are the cost of experimentation as well as the time required to conduct such experiments. This is also true for the study of porous medium where many researchers have relied on the numerical investigation of different phenomenon such as natural convection [1,2,3,4,5], mixed convection [6,7,8], viscous dissipation [9, 10], and non-equilibrium [11, 12] to name but a few. Among such phenomenon, the double diffusion is also an important case where the heat and mass diffusion take place simultaneously due to gradients created by applied heat and mass concentration at different surfaces in the domain. The diffusion of mass can depend on its own variables such as Lewis number and buoyancy ratio apart from the parameters which are common for the heat transfer [13,14,15,16,17]. The mass transfer behavior is studied extensively for the cases where the single heat source in regular form exists. However, the effect of multiple heat sources on the behavior of especially mass transfer is yet to be reported. The current article is a step in that direction to know the scenario when the heat source is present at two places, i.e., one at the outside surface of the domain and another at the internal section of the porous medium. The high concentration exists at left surface and low concentration at right surface.
2 Analysis
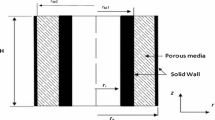
This work comprises the study of double diffusion due to multiple heat sources as shown in Fig. 1.
The related equations in porous domain can be derived from [18,19,20,21,22]
Expanding T 4 [23,24,25,26,27,28]
Boundary conditions are
At the strip
Finite element method as employed in references [29,30,31,32,33,34,35] is used to solve the equations.
3 Results and Discussion
Figure 2 depicts heat and mass diffusion with the help of the contours of temperature, concentration, and stream functions at Rd = 0.5, Ra = 100, Le = 5. N = 0.1, The left column shows the heating strip having the height 1/4th of cavity height and that of right column as ½ cavity height. The heat transfer should reduce from hot surface to the medium due to increase in the strip height which can be very much understood from the fact that the isotherm line with non-dimensional temperature of 0.95 has moved deep into the cavity. This ensures that the temperature gradient between two vertical surfaces and the cavity reduces, that in turn reduces the heat transfer. The mass transfer too is affected due to changing the strip height from 1/4th to ½ of cavity height. For the case of small strip height, the mass diffusion is more at the bottom of the cavity which can be observed through high concentration gradient at the lower part of the left surface and it decreases as the height of the left surface increases. This means that the mass transfer decreases from bottom of left surface until the top. However, the increase in the height of inside heater changes this scenario and the mass transfer across the left vertical surface remains almost constant which is indicated by almost straight concentration lines along that surface. There is large variation in concentration gradient in upper part of cavity due to increased strip height as compared to its smaller height. The streamlines mainly flow between the hot strip and the cold surface when strip height is more in comparison with lower height.
Figure 3 depicts buoyancy ratio (N) at Ra = 100, Rd = 0.5, St = 1/3, Le = 5, which is one of the important parameter to determine mass transfer. Heat transfer slightly decreases with increase in N which can be inferred from the isotherms. However, the concentration lines are seen to be aligned more closely to the left surface when the value of buoyancy ratio is increased as shown by the iso-concentration on right column of Fig. 3. The fluid movement changes the direction to more on left to right from being top to bottom surface when the buoyancy ratio is increased.
Figure 4 depicts another important parameter from mass transfer perspective, i.e., Lewis number (Le) at Ra = 100, Rd = 0.5, N = 0.3, St = 1/3. The left column of figure corresponds to Le = 1 and that of right column to Le = 10. The isotherms are not much affected though it comes slightly closer to hot surface when Le is increased. However, there is drastic change in the shape of iso-concentration lines when Le is increased from 1 to 10. At Le = 1, the concentration lines are highly spread out from each other that shows that the concentration gradient is smaller at Le = 1. The concentration lines come very close to the left surface at increased Le (Le = 10) which create high concentration gradient. This leads to substantially enhanced mass transfer as compared to the case of Le = 1. The fluid flow pattern is also affected when Le is changed. At higher values of Le, the fluid cell flows from top to bottom, whereas its orientation is more toward left to right surface at Le = 1.
4 Conclusion
This study aims to know multiple heating effects on double diffusion in a porous material. The study evaluates the effect of hot strip, the Lewis number, buoyancy ratio. It is noted that the
-
Heat transfer decreased when height of the strip is increased.
-
The mass transfer attains almost constant value all along the vertical surface when strip is elongated.
-
Fluid orientation changes due to increased strip height.
-
Mass transfer is highly sensitive to the Lewis number.
References
Badruddin IA, Zainal ZA, Narayana PAA, Seetharamu KN (2006) Heat transfer by radiation and natural convection through a vertical annulus embedded in porous medium. Int Commun Heat Mass Transf 33(4):500–507
Badruddin IA, Zainal ZA, Khan ZA, Mallick Z (2007) Effect of viscous dissipation and radiation on natural convection in a porous medium embedded within vertical annulus. Int J Therm Sci 46(3):221–227
Ahamad NA, Athani A, Badruddin IA (2018) Heat transfer prediction in a square porous medium using artificial neural network. AIP Conf Proc 1953:140017. https://doi.org/10.1063/1.5033192
Athani A, Ahamad NA, Badruddin IA (2018) Application of artificial neural network for heat transfer in porous cone. AIP Conf Proc 1953:140016. https://doi.org/10.1063/1.5033191
Badruddin IA, Al-Rashed AAAA, Ahmed NJS, Kamangar S, Jeevan K (2012) Natural convection in a square porous annulus. Int J Heat Mass Transf 55(23–24):7175–7187
Ahmed NJS, Badruddin IA, Kanesan J, Zainal ZA, Ahamed KSN (2011) Study of mixed convection in an annular vertical cylinder filled with saturated porous medium, using thermal non-equilibrium model. Int J Heat Mass Transf 54(17–18):3822–3825
Baig MAA, Salman Ahmed NJ, Ameer Ahamad N, Kamangar S, Reddy AR, Badruddin UA (2019) Discrete heating at bottom of annulus in case of mixed convection: aiding flow. AIP Conf Proc 2200:020051. https://doi.org/10.1063/1.5141221
Baig MAA, Salman Ahmed NJ, Ameer Ahamad N, Reddy AR, Badruddin IA, Mangesh L (2019) Discrete heating of opposing mixed convection heated at bottom of annulus. AIP Conf Proc 2200:020050. https://doi.org/10.1063/1.5141220
Khan TMY, Baig MAA, Azeem NA, Ahamad IA, Badruddin (2019) Heat and mass transfer with viscous dissipation in porous medium: FEM based methodology. AIP Conf Proc 2104(1):030058. https://doi.org/10.1063/1.5100485
Kamangar S, Baig MAA, Azeem NA, Ahamad IA Badruddin (2019) Finite element solution strategy for viscous dissipation in porous medium. AIP Conf Proc 2104(1):030057. https://doi.org/10.1063/1.5100484
Badruddin IA (2020) Thermal non-equilibrium in porous annulus: a new finite element solution technique. Arab J Sci Eng 45(2):1279–1292. https://doi.org/10.1007/s13369-019-04298-4
Badruddin IA (2019a) Numerical analysis of thermal non-equilibrium in porous medium subjected to internal heating. Mathematics 7(11):1085. https://doi.org/10.3390/math7111085
Baig MAA, Azeem NJ, Ahmed S, Kamangar S, Yunus Khan TM, Badruddin IA, Reddy AR, Khaleed HMT (2020) Finite element formulation of conjugate double diffusion in porous annulus. AIP Conf Proc 2204:040017. https://doi.org/10.1063/1.5141590
Badruddin IA, Ahmed NJS, Anqi AE, Kamangar S (2019) Conjugate heat and mass transfer in a vertical porous cylinder. J Thermophys Heat Transf 33(2):548–558. https://doi.org/10.2514/1.T5488
Badruddin IA, Ahmed NJS, Al-Rashed AAAA, Kanesan J, Kamangar S, Khaleed HMT (2012) Analysis of heat and mass transfer in a vertical annular porous cylinder using FEM. Transp Porous Media 91(2):697–715
Ahmed NJS, Badruddin IA, Zainal ZA, Khaleed HMT, Kanesan J (2009) Heat transfer in a conical cylinder with porous medium. Int J Heat Mass Transf 52(13–14):3070–3078
Badruddin IA, Azeem K, Idris MYI, Nik-Ghazali N, Ahmed NJS, Abdullah AAA, Al-Rashed (2017) Simplified finite element algorithm to solve conjugate heat and mass transfer in porous medium. Int J Numer Methods Heat Fluid Flow 27(11):481–2507
Azeem MEM, Soudagar NJS, Ahmed IA, Badruddin (2017) Fem formulation for heat and mass transfer in porous medium. In: IOP conference series: materials science and engineering 225:012022. https://doi.org/10.1088/1757-899X/225/1/012022
Azeem, Badruddin IA, Idris MYI, Nik-Ghazali N, Ahmed NJS, Al-Rashed A (2016) Conjugate heat and mass transfer in square porous cavity. Indian J Pure Appl Phys 54:777–786
Badruddin IA (2019b) Heat and mass transfer with soret/dufour effect in irregular porous cavity. J Thermophys Heat Transf 33(3):647–662. https://doi.org/10.2514/1.T5666
Badruddin IA, Abdullah AAAA, Ahmed NJS, Kamangar S (2012) Investigation of heat transfer in square porous-annulus. Int J Heat Mass Transf 55(7–8):2184–2192
Nik-Ghazali N, Badruddin IA, Badarudin A, Tabatabaeikia S (2014) Dufour and Soret effects on square porous annulus. Adv Mech Eng 6:209753
Ahamad NA, Kamangar S, Badruddin IA (2019) Heat transfer in a porous cavity in presence of square solid block. Int J Numer Meth Heat Fluid Flow 29(2):640–656. https://doi.org/10.1108/HFF-05-2017-0193
Badruddin IA, Khan IA (2017) Heat transfer in an l shaped porous medium using FEM. In: IOP conference series: materials science and engineering, vol 225, p 012012. https://doi.org/10.1088/1757-899X/225/1/012012
Badruddin IA (2019c) Investigation of heat transfer in irregular porous cavity subjected to various boundary conditions. Int J Numer Meth Heat Fluid Flow 29(1):418–447. https://doi.org/10.1108/HFF-04-2018-0132
Azeem MEM, Soudagar, Badruddin IA (2017) Investigation of heat transfer due to isothermal heater in irregular porous cavity: part I. AIP Conf Proc 1859:020044. https://doi.org/10.1063/1.4990197
Azeem IA, Badruddin N, Nik-Ghazali, Idris MYI, Anqi AE, Ahmed NJS, Kamangar S, Al-Rashed (2018) Effect of size and location of solid on conjugate heat transfer in porous cavity. Indian J Pure Appl Phys 56:792–801
Ahamad NA, Baig MAA, Ahmed NJS, Kamangar S, Khan TMY, Badruddin IA, Reddy AR, Khaleed HMT (2020) Finite element formulation of conjugate heat transfer in porous annulus. AIP Conf Proc 2204:040016. https://doi.org/10.1063/1.5141589
Yunus Khan TM, Badruddin IA, Quadir GA (2016) Heat transfer in a conical porous cylinder with partial heating. In: IOP conference series: materials science and engineering, vol 149, p 012211
Ahamad NA, Baig MAA, Kamangar S, Khan TMY, Badruddin IA (2019) Partial heating at upper section of annulus subjected to conjugate heat transfer in porous annulus. AIP Conf Proc 2105(1):020021. https://doi.org/10.1063/1.5100706
Ahamad NA, Baig MAA, Kamangar S, Khan TMY, Badruddin IA (2019) Conjugate heat transfer due to partial isothermal heating at center of annuls with two solids in porous annulus: part I. AIP Conf Proc 2105(1):020020. https://doi.org/10.1063/1.5100705
Azeem, Baig MAA, Khaleed HMT, Kamangar S, Badruddin IA (2019) Partial heating at lower section of annulus subjected to conjugate heat transfer in porous annulus. AIP Conf Proc 2105(1):020019. https://doi.org/10.1063/1.5100704
Ahmed NJS, Kamangar S, Badruddin IA, Al-Rashed AAAA, Quadir GA, Khaleed HMT, Khan TMY (2014) Conjugate heat transfer in porous annulus. J Porous Media 19(12):1109–1119
Badruddin IA, Ahmed NJS, Al-Rashed AAA, Nik-Ghazali N, Jameel M, Kamangar S, Khaleed HMT, Khan TMY (2015) Conjugate heat transfer in an annulus with porous medium fixed between solids. Transp Porous Media 109(3):589–608
Ahamad NA, Soudagar MEM, Kamangar S, Badruddin IA Fem formulation of coupled partial differential equations for heat transfer. In: IOP conference series: materials science and engineering 225:012023. https://doi.org/10.1088/1757-899X/225/1/012023.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Ameer Ahamad, N., Azeem, Baig, M.A.A., Praveen Kumar, A. (2020). Double Diffusion Due to Centrally Heated Strip in Porous Material. In: Praveen Kumar, A., Dirgantara, T., Krishna, P.V. (eds) Advances in Lightweight Materials and Structures . Springer Proceedings in Materials, vol 8. Springer, Singapore. https://doi.org/10.1007/978-981-15-7827-4_73
Download citation
DOI: https://doi.org/10.1007/978-981-15-7827-4_73
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-15-7826-7
Online ISBN: 978-981-15-7827-4
eBook Packages: Chemistry and Materials ScienceChemistry and Material Science (R0)