1 Introduction

The study of heat transfer in porous medium has attracted the attention of many researchers over the years. The prime reason for this interest can be directly linked with the fact that the porous medium is involved in plenty of applications covering a vast range of scientific and engineering disciplines. Some of the examples of porous medium application can be found in the processes of heat extraction from geothermal sources, heat removal from nuclear reactor, heat exchangers, electronic components, solar energy storage technology, exothermic reactions in packed bed reactors, storage of grains, food processing, high-performance insulation for energy-efficient buildings, and the spread of pollutants underground to name but few. The deep insight and further applications of porous medium can be found in the well-documented books such as Nield and Bejan (2006), Pop and Ingham (2001), Vafai (2000). The phenomenon of natural convective heat transfer inside the porous medium has been investigated and documented in great details. Natural convection in porous medium refers to the condition when specific segment of the medium, generally boundaries, is subjected to differential heating which in turn creates a density difference between warm and cold fluid of medium, thus setting the fluid into motion. The moving fluid carries certain amount of heat alongside its motion making the heat transfer a complex phenomenon. The study carried out emphasizing the analyses of natural convection in different geometries fixed with porous medium witnesses the research interest exhibited in this area (Salman et al. 2009; Badruddin et al. 2006a, b, 2007a, b). The heat transfer in porous medium is affected by many factors, and one of them is the case when solid wall having certain thickness is present alongside the porous medium. The presence of the solid wall affects the heat flow pattern inside the porous medium. This happens because of the fact that the boundary conditions are generally known at outer boundaries of the whole solid–porous system, but no information is available at the meeting point of solid and the porous region which can be termed as solid–porous interface. Thus, the heat transfer in the porous medium is dictated by the solid wall characteristics. This particular case when heat flow pattern is affected due to the presence of solid wall is referred to as conjugate heat transfer. The mathematical modeling of conjugate heat transfer requires an additional equation describing the heat transfer inside the solid wall apart from the usual momentum and energy equations of the porous region. There is relatively scarcity of literature pertaining to the conjugate heat transfer as compared to the heat transfer in porous medium without solid wall. There are various physical and geometrical parameters which affect the conjugate heat transfer rate, and in case of condensation process involving porous medium, the ratio of thermal resistance between the film condensation and the solid plate has great influence on determining the heat transfer characteristics of solid porous domain (Char and Lin 2001). It is established that the presence of a solid strip with heat generation can modify the temperature profile substantially in the porous medium (Mendez et al. 2002). It is reported that the reduction in aspect ratio by 25 % in a horizontal plate kept below the porous medium leads to 30–45 % reduction in temperature rise in the solid plate for Rayleigh number ranging from 1 to 1000 (Vaszi et al. 2001), and the plate thickness plays an important role in boundary layer formation (Vaszi et al. 2002). It is also noticed that in case of a solid cylindrical fin in porous medium, the local heat transfer coefficient and the local heat flux show a more gradual drop along the rounded tip as the aspect ratio of the fin becomes larger (Vaszi et al. 2004). In case of a horizontal solid strip dividing two porous media, the heat transfer rate is found to be stronger when the hot porous medium is below the strip than the other way round (Higuera 1991). The conjugate heat transfer in various shapes of porous media is reported in the literature which includes a semi-infiniteporous medium adjacent to solid wall (Pop and Merkin 1995), bidisperse porous channel (Nield and Kuznetsov 2004), porous channel (Shohel and Roydon 2005), square cavity fixed with solid wall on the left side of the cavity (Abdalla et al. 2008; Saeid 2007a; Baytaş et al. 2001; Saleh and Hashim 2012), square cavity embedded with a small solid heat source at the bottom surface of the cavity (Aleshkova and Sheremet 2010), vertical slender hollow cylinder (Pop and Na 2000; Ahmet Kaya 2011), and vertical cylinder with solid at inner radius (Salman et al. 2014). Apart from the above-mentioned cases, a porous cavity sandwiched between two solids has also been reported (Saeid 2007b; Alhashash et al. 2013). In this particular case, two solid walls having equal thickness and thermal conductivities are placed at left and right side of porous medium with boundary conditions applied at the solids walls. It is noticed that the conjugate heat transfer in an annular vertical cylinder having unequal thickness and thermal conductivities is not reported thus far to the best of author’s knowledge. The annular porous medium sandwiched between inner and outer solids can be used in refineries and exhaust chimney where the hollow portion of the cylinder could be carrying the hot fluid and the solid–porous–solid could be acting as a composite wall.

2 Mathematical Model

The schematic representation of the physical model showing the conjugate heat transfer in an annular porous annulus along with the coordinate system is depicted in Fig. 1. The coordinate system is chosen in such a way that the r- and z-axes point toward the radial and vertical directions respectively of the annulus. Since this is a conjugate problem, a solid wall with finite thickness exists at the inner and outer radii of the annulus. The porous medium is sandwiched between these two solid walls. The solid wall thickness is defined as a fraction of the total thickness of the annulus between inner and outer radii. DL and DR refer to the fraction of solid wall at inner and outer surfaces, respectively. The conductivity ratio Kr indicates the ratio of thermal conductivity between inner solid to porous medium where as solid conductivity ratio Krs is the ratio of inner to outer wall thermal conductivity. The inner surface of the annulus is heated to constant temperature \(T_{h}\), and the outer surface is maintained at constant temperature \(T_{\infty }\) such that \(T_{h} >T_{\infty }\).

Fig. 1
figure 1

Schematic of the physical model

Full size image

The following assumptions are applied

  1. (a)

    The fluid obeys Darcy law.

  2. (b)

    The convective fluid and the porous medium are in local thermal equilibrium.

  3. (c)

    There is no phase change of fluid in the medium.

  4. (d)

    The properties of the solid, fluid, and those of the porous medium are homogeneous

  5. (e)

    Fluid properties are constant except the variation in density with temperature.

The equations which dictate the heat and fluid flow in the porous solid regions of the domain are given by:

For porous region

$$\begin{aligned}&\displaystyle \frac{\partial (ru)}{\partial r}+\frac{\partial (rw)}{\partial z}=0 \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle \frac{\partial w}{\partial r}-\frac{\partial u}{\partial z}=\frac{gK\beta }{\nu }\frac{\partial T}{\partial r} \end{aligned}$$
(2)
$$\begin{aligned}&\displaystyle u\frac{\partial T_{p} }{\partial r}+w\frac{\partial T_{p} }{\partial z}=\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T_{p} }{\partial r}} \right) +\frac{\partial ^{2}T_p }{\partial z^{2}} \end{aligned}$$
(3)

For solid wall:

$$\begin{aligned} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T_{s} }{\partial r}} \right) +\frac{\partial ^{2}T_{s} }{\partial z^{2}}=0 \end{aligned}$$
(4)

Subjected to boundary conditions:

$$\begin{aligned}&\hbox {at}\quad \qquad r=r_{i}, \qquad \quad T_{s1} =T_{h} \end{aligned}$$
(5a)
$$\begin{aligned}&\hbox {at}\qquad \quad r=r_{o}, \qquad \quad T_{s2} =T_{\infty } \end{aligned}$$
(5b)

Since there is no heat storage in the medium, the following condition at solid–porous interface has to be satisfied

$$\begin{aligned}&\hbox {at} \qquad \quad r=r_{sp1}\qquad \quad u=0 \qquad \quad T_{s1} =T_{p} \qquad \quad k_{si} \frac{\partial T_{s1} }{\partial r}=k_{p} \frac{\partial T_{p} }{\partial r} \end{aligned}$$
(5c)
$$\begin{aligned}&\hbox {at}\qquad \quad r=r_{sp2} \qquad \quad u=0 \qquad \quad T_{p} =T_{s2} \qquad \quad k_{p} \frac{\partial T_{p} }{\partial r}=k_{s2} \frac{\partial T_{s2} }{\partial r} \end{aligned}$$
(5d)

The continuity Eq. (1) can be satisfied automatically by introducing the stream function \(\uppsi \) as:

$$\begin{aligned} u= & {} -\frac{1}{r}\frac{\partial \psi }{\partial z} \end{aligned}$$
(6a)
$$\begin{aligned} w= & {} \frac{1}{r}\frac{\partial \psi }{\partial r} \end{aligned}$$
(6b)

The following parameters have been used for non-dimensionalisation of the governing equations.

$$\begin{aligned}&\overline{r} =\frac{r}{L}\quad , \qquad \quad \overline{z} =\frac{z}{L}, \quad \qquad \overline{\psi }=\frac{\psi }{\alpha \varphi L}, \quad \qquad \overline{T} =\frac{\left( {T-T_{\infty } } \right) }{\left( {T_{h} -T_{\infty }} \right) }\nonumber \\&Ra=\frac{g\beta \Delta TKL}{\nu \alpha _{f} } \end{aligned}$$
(7)

Substitution of Eqs. [SubEquationDirect](6a)–(7) into Eqs. (2)–(4) results in:

$$\begin{aligned}&\displaystyle \frac{\partial ^{2}\overline{\psi }}{\partial \overline{z} ^{2}}+\bar{{r}}\frac{\partial }{\partial \overline{r} }\left( {\frac{1}{\bar{{r}}}\frac{\partial \overline{\psi }}{\partial \overline{r} }} \right) =\bar{{r}}Ra\frac{\partial \overline{T_{f} } }{\partial \overline{r} } \end{aligned}$$
(8)
$$\begin{aligned}&\displaystyle \frac{1}{\bar{{r}}}\left[ {\frac{\partial \overline{\psi }}{\partial \overline{r} }\frac{\partial \overline{T_{p} } }{\partial \overline{z} }-\frac{\partial \overline{\psi }}{\partial \overline{z} }\frac{\partial \overline{T_{p} } }{\partial \overline{r} }} \right] =\frac{1}{\bar{{r}}}\frac{\partial }{\partial \bar{{r}}}\left( {\bar{{r}}\frac{\partial \overline{T_{p} } }{\partial \overline{r} }} \right) +\frac{\partial ^{2}\overline{T_{p} } }{\partial \overline{z}^{2}} \end{aligned}$$
(9)
$$\begin{aligned}&\displaystyle \frac{1}{\bar{{r}}}\frac{\partial }{\partial \bar{{r}}}\left( {\bar{{r}}\frac{\partial \overline{T_{s} } }{\partial \overline{r} }} \right) +\frac{\partial ^{2}\overline{T_{s} } }{\partial \overline{z} ^{2}}=0 \end{aligned}$$
(10)

The boundary conditions take the form as:

$$\begin{aligned}&\hbox {at}\qquad \quad \bar{{r}}=r_{i} \qquad \quad \bar{{T}}_{s1} =1 \end{aligned}$$
(11a)
$$\begin{aligned}&\hbox {at}\qquad \quad \bar{{r}}=r_{o} \qquad \quad \bar{{T}}_{s2} =0 \end{aligned}$$
(11b)
$$\begin{aligned}&\hbox {at}\qquad \quad \bar{{r}}=r_{sp1} \qquad \quad \bar{{\psi }}=0,\quad \qquad \bar{{T}}_{s1} =\bar{{T}}_p \qquad \quad Kr\frac{\partial \bar{{T}}_{s1} }{\partial \bar{{r}}}= \frac{\partial \bar{{T}}_{p}}{\partial \bar{{r}}} \end{aligned}$$
(11c)
$$\begin{aligned} \hbox {at} \,\,\,\quad \quad \bar{{r}}=r_{sp2} \qquad \quad \bar{{\psi }}=0, \quad \qquad \bar{{T}}_{p} =\bar{{T}}_{s2} \qquad \quad \frac{\partial \bar{{T}}_{p}}{\partial \bar{{r}}}=Kr_{o} \frac{\partial \bar{{T}}_{s2} }{\partial \bar{{r}}} \end{aligned}$$
(12)

The Nusselt number is calculated using following expressions:

$$\begin{aligned} \bar{{N}}u=-\frac{1}{\bar{{z}}}\int \limits _{0}^{\bar{{z}}} {\left( {\frac{\partial \bar{{T}}_{p} }{\partial \bar{{r}}}} \right) _{\bar{{r}} = \bar{{r}}_{sp1} } \mathrm{d}\bar{{z}}} \end{aligned}$$
(13)

3 Numerical Scheme

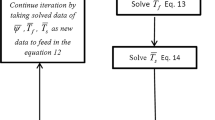
The equations that govern the heat transfer in solid section along with heat and fluid flow inside the porous medium are partial differential equations. These are coupled equations (Eqs. 8–10) having interdependency on each other. Any change in one equation affects the other equation and vice versa which makes them difficult to solve directly. Thus, these equations are to be solved simultaneously. Current numerical scheme is based on finite element method where Eqs. 8–10 are converted into algebraic form of equations with the help of Galerkin method (Segerland 1982; Lewis et al. 2004). The resultant set of algebraic equations is assembled into a global matrix for each of the Eqs. 8–10. It requires only a half of the domain to be modeled due to symmetric nature of the cylinder. A 3-noded triangular element is used to mesh the domain. The accuracy of finite element method generally depends on the number of elements being chosen to mesh the domain, and it increases with increase in number of elements until a point, thereafter the dependency becomes irrelevant. The geometry is meshed with sufficient number of elements to make sure that the results are not affected due to mesh size. Equations 8–10 are solved iteratively with tolerance level for \(\bar{{\psi }}\) and \(\bar{{T}}\) are set as \(10^{-7}\) and \(10^{-5}\), respectively. The tolerance level indicates the difference in the value of solution variable \((\bar{{\psi }}\) and \(\bar{{T}})\) from its previous iteration for each of the nodes in the domain. The present methodology is validated with the previously published data by setting the solid wall thickness to zero that corresponds to vertical annular porous medium. The comparison is shown in Table 1 to illustrate that the current method is accurate enough to simulate the heat transfer behavior of problem under consideration.

Table 1 Comparison of results for different aspect ratio at \(Ra=100,\;Rr=1,DL=DR=0\)
Full size table

4 Results and Discussion

The problem under investigation is discussed for different physical and geometric parameters involved. Emphasis is given to the thickness of the solid walls at the inner and outer surfaces along with the conductivity ratio and solid conductivity ratio. Results are discussed in terms of Nusselt number at the solid–porous interface which is a measure of heat transfer from the solid wall to porous medium. Apart from Nusselt number, the temperature distribution at the solid–porous interface and the streamlines along with isothermal lines are presented for various physical and geometric parameters.

4.1 Temperature Profile

The boundary conditions of current problem are such that the inner and outer surfaces are maintained at \(T_{h}\) and \(T_{\infty }\), respectively, which means that the heat has to travel from inner radius toward outer radius because of temperature difference in radial direction. The applied temperature exists on the left and right surfaces of the inner and outer solid walls. The heat transfer from solid wall to the porous medium and then from porous medium to outer solid depends on the temperature profile at the solid–porous interfaces. These profiles are in turn dependent on the solid wall thickness and the physical properties of walls. Since the domain includes two solid walls at inner and outer surfaces, it is important to know the temperature variations along the interfaces and the medium to judge the heat transfer characteristics of the whole domain.

Figures 2, 3 illustrate the effect of solid wall thickness on the temperature distribution at the inner and outer surface solid porous interfaces for DL = 3.125, 6.25, 12.5, 25,37.5 & 50 % at \({\textit{DR}} = 6.25\) and 25 %. Figures 2, 3, 4, and 5 correspond to \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 2\). It is observed that the temperature of solid–porous interface at \(r_{sp1}\) is very close to that of the applied temperature \(T_{h}\) when the wall thickness DL is small but the temperature of interface at higher values of DL is substantially different from that of \(T_{h}\). This is because the conduction resistance is low when left wall is thinner, thus facilitating the heat transfer in the inner solid that in turn increases the temperature across the inner solid. The temperature increases along the height of the cylinder. The variation in temperature at lower section of the cylinder is sharp as compared to other sections. The fluid movement near the interface creates sharp variation in temperature at the lower part of cylinder by absorbing heat near that region and then moving upwards where the already elevated fluid temperature does not allow further absorption of heat due to reduced temperature difference between fluid and the interface region at upper section of cylinder. The increase in the wall thickness at outer surface, DR does not affect the interface temperature \(T_{sp1}\) for lower values of DL. However, the increase in DR reduces the interface temperature at upper section of cylinder for higher value of DL. The trend of temperature variation \(T_{sp2}\) for the porous–solid interface at outer surface as shown in Fig. 3 is completely different from that of inner surface temperature \(T_{sp1}\). At \(r_{sp2,}\) the temperature increases gradually for most of the cylinder height until almost Ar = 75 %, and then, the increase is rapid for upper section. The fluid which has brought energy from \(r_{sp1}\) losses its most of the heat to the upper part of \(r_{sp2}\); thus, temperature in that region is higher as compared to the other sections of the interface \(r_{sp2}\). At lower part of cylinder and given value of \(\bar{{z}}\), the temperature is higher for higher inner wall thickness. This could be due to the reason that the fluid does not have enough strength to flow closer to lower part of \(r_{sp2}\) when width of porous medium is higher because of thinner DL. However, the fluid is forced to flow near to \(r_{sp2}\) when porous medium becomes thinner due to higher DL, resulting in better transfer of thermal energy in that vicinity of annulus. It is also observed that the temperature along \(r_{sp2}\) is higher for higher wall thickness at outer surface. The increased wall thickness DR is achieved at the cost of reduced porous thickness which in turn decreases thermal resistance along the depth of porous medium, thus increasing the temperature along \(r_{sp2}\) as depicted in Figs. 4, 5. It could be noted that Fig. 5 shows the temperature variation for two values of Krs which indicates the relative thermal conductivity of two solid walls. In Fig. 5, the height of the cylinder varies from left to right for \({ Krs} = 2\) and right to left for Krs = 0.5. Figures 6 and 7 illustrate the effect of solid conductivity ratio Krs on interface temperature \(r_{sp1}\) and \(r_{sp2}\), respectively. These figures correspond to the values \({\textit{Ra}}=300, {\textit{Rr}}=1,\;{\textit{Ar}}=5\), when both the solid walls have equal thickness of 6.25 and 25 %. The temperature along \(r_{sp1}\) does not vary much for higher wall thickness. It is seen that the \(T_{sp1}\) is higher when the conductivity of left solid wall is higher than the solid wall at outer surface of cylinder leading to higher value of Krs, for a given value of porous medium thermal conductivity. It can be reasoned that the higher conductivity of inner solid facilitates greater heat transfer leading to increased temperature \(T_{sp1}\). The effect of Krs reduces considerably when the porous conductivity is much lesser than the inner surface solid wall conductivity (higher Kr).

Fig. 2
figure 2

Temperature along \(\hbox {r}_{sp1}\hbox {when}\) DL varies

Full size image
Fig. 3
figure 3

Temperature along \(\hbox {r}_{sp2}\) when DL varies

Full size image
Fig. 4
figure 4

Temperature along \(\hbox {r}_{sp2}\) when DR varies

Full size image
Fig. 5
figure 5

Temperature along \(\hbox {r}_{sp2}\) when DR varies

Full size image
Fig. 6
figure 6

Temperature along \(\hbox {r}_{sp1}\) when Krs varies

Full size image
Fig. 7
figure 7

Temperature along \(\hbox {r}_{sp2}\) when Krs varies

Full size image

4.2 Streamlines and Isotherms

The fluid flow pattern and the temperature variation in the domain can be well described with the help of streamlines and the isothermal lines which basically represent the areas of constant values of stream function and the temperature. The effect of solid wall thickness variation when \({ DL} = {\textit{DR}}\) is shown in Fig. 8. This figure is obtained by setting \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\). Isotherms are placed left and streamlines on right side of the figure for three values of inner and outer wall thickness. It is seen that the left solid wall is occupied by high-temperature lines, indicating that higher amount of energy is transferred from inner radius to \(r_{sp1}\) because of high conductivity of the inner solid (\({{ Kr} = 10}\)). The outer solid is occupied by low-temperature isotherms because of low conductivity of outer solid. At low values of DL/DR, the fluid gains thermal energy at the lower left segment of cylinder and then moves toward the right upper segment losing its energy to outer surface before flowing back toward the left segment of cylinder, thus completing the cycle. The flow pattern is oval-shaped from lower left to upper right segment of the annulus. The increased wall thickness shifts the flow direction from being oval to near elliptical from bottom to top of the annulus.

Fig. 8
figure 8

Isotherms (left) , streamlines (right) for a \(\textit{DL} = \textit{DR} = 6.25\,\%\), b \(\textit{DL} = \textit{DR} = 12.5\,\%\), c \(\textit{DL} = \textit{DR} = 25\,\%\) at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\)

Full size image

Figure 9 indicates the effect of varying inner solid wall thickness by keeping the constant values \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\), \({ DR} = 6.25\,\%\). There is slight straightening of isotherms with increase in the wall thickness which indicates that the convection has reduced. This is further vindicated by reduction in the value of streamlines with increase in DL. The reduced stream function leads to reduction in the fluid velocity which in turn retards the heat transfer rate at the solid porous interface. The effect of varying the outer wall thickness is shown in Fig. 10 which is obtained at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\), \({ DL} = 3.125\%\). It is obvious from Fig. 10 that the isotherms have considerably straightened when DR is varied from 6.25 to 50 %. This reflects that the heat transfer due to convection reduces when DR is increased. The value of stream function reduces with increase in DR. Thus, it can be said that the increase in the either wall thickness reduces the fluid velocity inside the porous medium.

Fig. 9
figure 9

Isotherms (left) , streamlines (right) for a \(\textit{DL} = 6.25\,\%\), b \(\textit{DL} = 12.5\,\%\), c \(\textit{DL} = 25\,\%\) at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\), \({ DR} = 6.25\,\%\)

Full size image
Fig. 10
figure 10

Isotherms (left) , streamlines (right) for a \(\textit{DR} = 6.25\,\%\), b \(\textit{DR} = 12.5\,\%\), c \(\textit{DR} = 25\,\%\) at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ Krs} = 5\), \({ DL} = 3.125\%\)

Full size image

The effect of solid conductivity ratio on the streamline and isotherms is shown in Fig. 11. This figure belongs to \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({ DL} = 12.5\%\), \({ DR} = 12.5\,\%\). The increase in solid conductivity ratio reduces the thermal gradient as indicated by spread out isotherms due to increase in Krs. The fluid velocity is reduced due to increase in Krs as indicated by streamlines.

Fig. 11
figure 11

Isotherms (left) , streamlines (right) for a \({\textit{Krs}} = 0.1\), b \({\textit{Krs}} = 1\), c \({ Krs} = 10\) at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\), \({\textit{DL}} = 12.5\,\%\), \({ DR} = 12.5\,\%\)

Full size image

Figure 12 demonstrates the effect of variation in thermal conductivity ratio Kr on streamlines and isotherms. This figure is obtained by maintaining \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Krs} = 10\) \({ DL} = 12.5\,\%\), \({ DR} = 12.5\,\%\). It is obvious from Fig. 12 that the fluid velocity increases with increase in thermal conductivity ratio. This can be attributed to the fact that the higher Kr is associated with increase in thermal conductivity of inner solid keeping the porous conductivity at constant value which in turn allows more heat to be transferred to porous medium leading to better fluid movement.

Fig. 12
figure 12

Isotherms (left), streamlines (right) for a \({ Kr} = 1\), b \({ Kr} = 5\), c \({ Kr} = 10\) at \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Krs} = 10\), \({ DL} = 12.5\,\%\), \({ DR} = 12.5\,\%\)

Full size image

4.3 Heat Transfer in the Domain

The heat transfer from inner radius toward outer radius of the annular solid–porous–solid domain can be described with the help of Nusselt number. Nusselt number basically highlights the convective heat transfer relative to conduction. The following section discusses the variation in Nusselt number due to changes in various physical and geometric parameters. Figure 13 shows the average Nusselt number at \(r_{sp1}\) due to change in DL. This figure is obtained by setting \({ Ra} = 200\), \({ Rr} = 1\), \({ Ar} = 5\), \({ Kr} = 10\). It is observed that the average Nusselt number \(\bar{{N}}u\) decreases with increase in the wall thickness DL for thin outer wall thickness. However, for thicker outer wall thickness, the \(\bar{{N}}u\) initially decreases with respect to DL and then increases with further increase in DL. The decrease in \(\bar{{N}}u\) with respect to increase in DL is a result of reduction in the \(T_{sp1}\) due to increased thermal resistance created by thickening solid wall at inner surface. However, the increase in the \(\bar{{N}}u\) at higher outer wall thickness is associated with increased thermal gradient across \(r_{sp1}\) which offsets the effect of decreased interface temperature \(T_{sp1.}\) The increase in the conductivity ratio Kr increases the heat transfer rate as indicated by Fig. 14 that belongs to \(Ra=100, Rr=1,\;Ar=1,DR=6.25\). The effect of Krs diminishes as the solid wall thickness DL increases. The \(\bar{{N}}u\) variation is almost linear when the relative conductivity of inner solid is high compared to that of porous conductivity.

The effect of outer wall thickness DR on heat transfer rate is depicted in Fig. 15 which is obtained by \(\hbox {setting } {\textit{Ra}}=100, {\textit{Rr}}=1,\;{\textit{Ar}}=1,{\textit{DR}}=6.25\). The Nusselt number decreases with increase in the DR. The variation in heat transfer with respect to change in DR is almost linear as shown in Fig. 15. The thermal conductivity ratio of inner and outer solids which is denoted by Krs plays an important role in determining the heat transfer characteristics inside the solid–porous–solid domain. The value \(\textit{Krs}>1\) indicates that the conductivity of inner solid is higher than that of outer solid and vise versa for \(\textit{Krs}<1\). The combination of different grades of aluminum at inner radius and steel at outer radii of annulus can have the Krs \(\approx \) 10. It is seen that the heat transfer rate decreases with increase in the Krs as illustrated by Fig. 16. The decrease in heat transfer with increase in Krs can be explained in a way that the increased solid conductivity ratio is associated with decrease in the thermal conductivity of outer solid. The decrease in the outer solid conductivity contributes to increase in the overall thermal resistance of porous–solid combination which in turn reduces the Nusselt number at \(r_{sp1}\). It is worth mentioning that the increase in Krs is associated either with increase in \(k_{s1 }\) or decrease in \(k_{s2}\). If Kr is fixed as in case of Fig. 16, then the only way to increase Krs is by decreasing \(k_{s2}\) that leads to higher thermal resistance of the outer wall and thus the whole domain, resulting into decreased heat transfer rate as shown in Fig. 16. However, this decrease is negligible when the decrease in \(k_{s2}\) is counterbalanced by increase in porous conductivity (low Kr) or thinning of inner or outer wall resulting into low thermal resistance of overall domain. The increase in Krs is also associated with increase in the inner wall conductivity \(k_{s1}\) by keeping outer solid conductivity at constant value. In such condition, the overall thermal resistance of the whole domain decreases due to increase in \(k_{s1}\) that in turn increases Kr and heat transfer rate as shown in Fig. 16 (\({\textit{Ra}}=100, {\textit{Rr}}=1,\;{\textit{Ar}}=1)\). The effect of Rayleigh number on Nusselt number is shown in Fig. 17 which is obtained at \({\textit{DL}}=12.5,\;{\textit{DR}}=12.5, {\textit{Rr}}=1,\;{\textit{Ar}}=10\). As expected, the heat transfer rate increases with increase in Rayleigh number. For a given value of Krs, the effect of Rayleigh number is higher when Kr is high. The high Rayleigh number and Kr lead to increased fluid energy and thus velocity which reflects in the form of increased Nusselt number.

Fig. 13
figure 13

\(\bar{{N}}u\) variation with respect to DL

Full size image
Fig. 14
figure 14

\(\bar{{N}}u\) variation with respect to DL for various thermal conductivity ratios

Full size image
Fig. 15
figure 15

\(\bar{{N}}u\) variation with respect to DR

Full size image
Fig. 16
figure 16

\(\bar{{N}}u\) variation with respect to Krs

Full size image
Fig. 17
figure 17

Effect of Rayleigh number on \(\bar{{N}}u\)

Full size image

5 Conclusion

Conjugate heat transfer in an annular porous medium sandwiched between inner and outer solid walls is investigated with specific emphasis on the solid thickness and the conductivity ratio. Finite element method is used to solve the governing equations. It is found that there is not much temperature variation inside the inner solid when the wall thickness is small. The temperature at solid porous interface \(r_{sp1}\) increases along the height of the cylinder. At \(r_{sp2,}\) the temperature increases gradually for most of the cylinder height until almost \({ Ar} = 75\,\%\) and then, the increase is rapid for upper section. It is also observed that the temperature along \(r_{sp2}\) is higher for higher wall thickness at outer surface. It is observed that the average Nusselt number decreases with increase in the wall thickness DL for thin outer wall thickness. However, for thicker outer wall thickness, the \(\bar{{N}}u\) initially decreases with respect to DL and then increases with further increase in DL. The increase in the conductivity ratio Kr increases the heat transfer rate. The effect of Krs diminishes as the solid wall thickness DL increases. It seems that the heat transfer rate decreases with increase in the Krs.