Thermo-Mechanical Analysis of a Rotor-Bearing System Having a Functionally Graded Shaft with Transverse Breathing Cracks

Abstract

Purpose: The dynamic behavior of two-cracked functionally graded (FG) shaft system under thermal environment has been carried out. The finite element (FE)-based formulation is used to model metal-ceramic FG (SS/ZrO₂) shaft using Timoshenko beam theory (TBT). Power law of material gradation is used to derive effective thermo-elastic properties of radially graded FG shaft. Methods: The governing system equations of motion are formulated using Hamilton’s principle. The local flexibility coefficients (LFCs) are derived as functions of material gradient, temperature, size and orientation of crack, for the cracked FG circular cross-sectional FG shaft, using linear elastic fracture mechanics, Castigliano’s theorem and energy method. Results: Numerical simulations are performed to analyze the effects of geometric, material and temperature gradient parameters on the natural frequencies of the cracked FG shaft system. Conclusion: LFCs are functions of material gradient and temperature besides crack size. Even though the reduction in eigenfrequencies is decided by crack parameters, material gradient and temperature, however, the reduction in eigenfrequencies is greatly influenced by gradient index and the index may be selected properly to design FG shafts for high-temperature applications.

1 Introduction

In the improvement of structural performance, FG materials (FGMs) are used as multifunctional and high-performance materials in which thermo-elastic properties graded are followed by material gradation laws. FGMs offer numerous superior properties over laminated composite materials and are used mainly to reduce interlaminar stresses and delamination problem. Historically, the concept of gradation was first proposed [1] in 1972, for composites and polymeric materials. However, the work [1] was limited impact. FGMs were first introduced [2] in 1980s in Japan. Then, FGMs are rapidly becoming well known and widely used in aerospace, automotive, biomedical and so on. A lot of researches were reported on the behavior of FG structural systems with great interest during the last few years. Some of the important works in the directions are presented here. Thermo-mechanical responses of structure made of FG materials are studied by Reddy and Chin [3]. By using TBT, Piovan and Sampaio [4] developed a composite rotating nonlinear FG beam model accounting for arbitrary axial deformations. Gayen and Roy [5] carried out vibration and stability of a shaft made of FGMs and reported effect of gradient index on dynamic responses. Boukhalfa [6] studied dynamic responses of a spinning shaft made of FGMs using TBT.

Transverse cracks in structural members such as shaft and rotor lead dangerously to failure associated with economic loss and more importantly human life. The first studies on cracked rotors were started in the 1970s. Thereafter, several researchers reported the review works of cracked shaft and rotors [7]. Papadopoulos and Dimarogonas [8] derived local flexibility matrix and studied the coupled vibration for a shaft made of homogeneous materials. Jun et al. [9] carried out vibration characteristics of a cracked rotor based on fracture mechanics approach. Sinou and Lees [10] carried out dynamic response for a shaft using an alternate frequency/time domain approach. Coupled vibration responses [11] were reported for a breathing cracked shaft using nonlinear FE method. However, appearances of more than one crack in shafts create complication of obtaining the dynamic characteristics. Sekhar [12] carried out the eigenfrequencies and instability of a rotor system with two cracks. Vibration responses were reported by Darpe et al. [13] for a simple Jeffcott rotor with two cracks.

Crack in FG structure has vital role due to their safe performance for high demands in various engineering sectors. Yang and Chen [14] studied free vibration and buckling analysis of cracked FG Euler–Bernoulli beams. Aydin [15] reported free vibration of FG beams considering multiple edge cracks with different end conditions. Gayen et al. [16] modeled an FG shaft based on Euler–Bernoulli beam theory and studied the free vibration of the FG shaft system. Based on the FE analysis and considering TBT, a cracked FG shaft modeled and carried out the dynamic responses by Gayen et al. [17,18,19].

Therefore, the present study aims in analyzing the thermo-mechanical behavior of a multi-cracked rotor system with a shaft made of FGMs, using FE method. Numerical results are performed at determining the eigenfrequencies to understand the importance of shaft’s slenderness, number, size, location and orientation of crack, material gradient and temperature on the vibration responses of cracked FG shaft.

2 Thermo-Elastic Material Model

The effective thermo-elastic materials properties $C$ [20] for the FG shaft are obtained as

$${\text{C}}(T) = C_{0} (C_{ - 1} T^{ - 1} + 1 + C_{1} T + C_{2} T^{2} + C_{3} T^{3} )$$

(1)

where $C_{0} , \, C_{ - 1} , \, C_{1} , \, C_{2} {\text{ and }}C_{3}$ are temperature coefficients for each constituent materials.

For a shaft made of FGMs, the following power law of material gradation, $C$ [3], as functions of $y$ and temperature ($T$) is obtained

$$C\left( {y,T} \right) = C_{\text{m}} \left( T \right) + \left\{ {C_{\text{c}} \left( T \right) - C_{\text{m}} \left( T \right)} \right\}V_{\text{c}} \left( y \right)$$

(2)

where

$$\begin{aligned} & V_{\text{c}} \left( y \right) = \left\{ {{{\left( {y - R_{\text{m}} } \right)} \mathord{\left/ {\vphantom {{\left( {y - R_{\text{m}} } \right)} {\left( {R_{\text{c}} - R_{\text{m}} } \right)}}} \right. \kern-0pt} {\left( {R_{\text{c}} - R_{\text{m}} } \right)}}} \right\}^{k} , { }V_{\text{m}} ( y ) = 1 - V_{\text{c}} \left( y \right) , \\ \, & \quad R_{\text{c}} \le y \le R_{\text{m}} ,\,\,\,\,0 \le k \le \infty \\ \end{aligned}$$

(3)

Now, for radially graded FG shaft, temperature profile is obtained, using steady-state one-dimensional heat conduction equation as

$${{\text{d}} \mathord{\left/ {\vphantom {{\text{d}} {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}\left[ {yK(y){{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right] = 0$$

(4)

In solving Eq. (4) for a solid shaft, for temperature distribution at the center ($y = R_{\text{i}} = 0$), the solution becomes singular. This singularity could be handled by considering the inner radius $R_{\text{i}} = \varepsilon \simeq 0$. However, the solution depends upon the proper choice of $\varepsilon$ and needs a good amount of study to assure convergence. Therefore, a conservative approach is used to compute the eigenfrequencies considering uniform temperature ($T = T_{\text{o}}$, at any $y$) even though the actual temperature distribution will not be uniform. But the results could safely be used for the actual case where the temperature gradient exists.

3 Modeling of FG Shaft System Based on FE Method

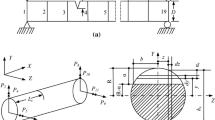
Using TBT, an FG shaft is modeled considering two-noded beam element with four degrees of freedom at each node. Figure 1a–d presents a rotor-disk-bearing system interconnecting the components such as cracked FG shaft, rigid disk and bearings.

Fig. 1

Cracked FG rotor system: a FE discretization, b crack orientation, c general loads, d cross section of cracked geometry

3.1 Cracked Shaft Element Made of FGM

Using Paris’s equations [21] and Castigliano’s theorem, the cross-coupled and direct LFCs are calculated with the expressions of stress intensity factors (SIFs). The additional displacement $u_{\text{i}}^{\text{c}}$ due to crack is

$$\begin{aligned} & u_{i}^{\text{c}} = \frac{\partial }{{\partial P_{i} }} \\ & \quad \int\limits_{0}^{{\mathop \alpha \nolimits_{x} }} {\frac{1}{E(y,T)}\left[ {\left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\text{I}}i}} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\text{{I}{I}}}i}} } } \right)^{2} + \{ 1 + \nu (y,T)\} \left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\text{{I}{I}{I}}}i}} } } \right)^{2} } \right]} {\text{d}}y \\ \end{aligned}$$

(5)

where $K_{\text{I}} , \, K_{\text{II}}\, {\text{ and }}K_{\text{III}}$ are SIFs for modes I, II, and III, respectively, and $i = 1,{\text{ 2, 3 and 4 }}$ are load indices.

Referring Fig. 1d, the LFCs for fully open crack $\theta = 180^{\text{o}}$ are obtained

$$\begin{aligned} & C_{ij}^{\text{c}} = \frac{{\partial u_{i}^{\text{c}} }}{{\mathop {\partial P}\nolimits_{j} }} = \frac{{\mathop \partial \nolimits^{2} }}{{\mathop {\partial P}\nolimits_{i} \mathop { \, \partial P}\nolimits_{j} }} \\ & \quad \int\limits_{ - b}^{b} {\int\limits_{0}^{{\mathop \alpha \nolimits_{x} }} {\frac{1}{E(y,T)}\left[ {\left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\rm I}i}} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\rm I}{\rm I}i}} } } \right)^{2} + \{ 1 + \nu (y,T)\} \left( {\sum\limits_{i = 1}^{4} {\mathop K\nolimits_{{{\rm I}{\rm I}{\rm I}i}} } } \right)^{2} } \right]{\text{d}}y {\text{d}}z} } \\ \end{aligned}$$

(6)

In Eq. (6), numerical integrations are performed to derive local flexibility matrix $\left[ {\mathop {\mathbf{C}}\nolimits^{{\mathbf{c}}} \left( {y,T} \right)} \right]$ and corresponding $\mathop {\mathbf{K}}\nolimits^{\text{c}}$ (cracked stiffness matrix) are derived following the works of Gayen et al. [17, 18].

The stiffness variation during the crack opening and closure, i.e., the breathing effect of the cracked rotor, is given following the work [10] as

$${\mathbf{K}}\left( t \right) = {\mathbf{K}}^{\text{uc}} - f(t){\mathbf{K}}^{\text{c}} {\text{ with }}f(t) = {{\left( {1 - \cos \, \Omega t} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \cos \, \Omega t} \right)} 2}} \right. \kern-0pt} 2}$$

(7)

where $f(t)$ is crack opening and closure function.

The equations of motion of the cracked shaft element are given as

$$\left( {\mathop {\mathbf{\rm M}}\nolimits_{\text{t}}^{\text{s}} + \mathop {\mathbf{\rm M}}\nolimits_{\text{r}}^{\text{s}} } \right) \, \mathop {{{\ddot{\mathbf{p}}}}}\nolimits^{\text{ s}} (t) - \Omega \mathop { \, {\mathbf{G}}}\nolimits^{\text{s}} \, \mathop {{\dot{\mathbf{p}}}}\nolimits^{\text{s}} (t){\mathbf{ + }}\mathop {\mathbf{K}}\nolimits^{\text{s}} \, \mathop {\mathbf{p}}\nolimits^{\text{s}} (t) = \mathop {\mathbf{f}}\nolimits^{\text{s}} (t)$$

(8)

where the elementary matrices are given in the works [17, 18].

3.2 System Equations of Motion and Solution

The resultant system equations of motion including the shaft, rigid disk and bearing are given

$$\begin{aligned}&\left( {\mathop {\mathbf{M}}\nolimits_{\text{t}}^{\text{s}} + \mathop {\mathbf{M}}\nolimits_{\text{r}}^{\text{s}} + \mathop {\mathbf{M}}\nolimits_{\text{t}}^{\text{d}} + \mathop {\mathbf{M}}\nolimits_{\text{r}}^{\text{d}} } \right){{\ddot{\mathbf{p}}}} + \left( {{\mathbf{C}}^{\text{b}} - \Omega {\mathbf{G}}^{\text{s}} - \Omega {\mathbf{G}}^{\text{d}} } \right){\dot{\mathbf{p}}} + \left( {{\mathbf{K}}^{\text{s}} + {\mathbf{K}}^{\text{b}} } \right){\mathbf{p}}\\ &\quad= \left\{ {{\mathbf{F}}^{\text{s}} (t) + {\mathbf{F}}^{\text{d}} (t) + {\mathbf{F}}^{\text{b}} (t)} \right\}\end{aligned}$$

(9)

For the analysis of natural whirling speeds of the rotor-bearing system with FG shaft, the force term can be omitted. Then, the final system equations of motion are given

$$\mathbf{M}{\ddot{\mathbf{p}}} + \mathbf{C}\dot{\mathbf{p}} + \mathbf{Kp} = \{ 0\}$$

(10)

For Eq. (10), the eigenvalue solution is $\lambda_{n} \left( \Omega \right) = \xi_{n} \left( \Omega \right) \pm i\omega_{n} \left( \Omega \right)$, logarithmic decrement is $\delta_{n} = {{ - 2\pi \xi_{n} } \mathord{\left/ {\vphantom {{ - 2\pi \xi_{n} } {\omega_{n} }}} \right. \kern-0pt} {\omega_{n} }}$ and stability threshold speed is obtained for $\delta_{n} = 0$.

4 Results and Discussion

Here, a cracked FG shaft with diameter $D = 0.1{\text{ m}}$ and temperature-dependent material properties of the constituents of the FG (SS/ZrO₂) are considered same as in [20]. Density for SS and ZrO₂ is 8166 and 5700 kg/m³, respectively. The shaft is discretized with 25 finite elements; simply supported (S–S) and flexible end condition is considered for dynamics of shafts. A disk is located at midspan of the shaft with weight 1.406 kg, $I_{\text{p}}^{\text{s}}$ and $I_{\text{d}}^{\text{s}}$ 0.002 and 0.0135 kg-m², respectively.

Due to lack of appropriate results for dynamic characteristics of FG shafts, the present crack formulation has been validated in two steps. First, computed natural frequencies are compared with classical solution and results. Table 1 shows an excellent agreement with the closed-form solutions, thereby validating the FE formulation of homogeneous beam and developed code.

Table 1 Evaluation of fundamental frequency (in Hz) for a homogeneous beam

Second, dimensionless natural frequencies are computed for the first crack size ${{\alpha_{1} } \mathord{\left/ {\vphantom {{\alpha_{1} } {R = 0.2}}} \right. \kern-0pt} {R = 0.2}}$, first crack location ${{L_{{{\text{c}}1}} } \mathord{\left/ {\vphantom {{L_{{{\text{c}}1}} } L}} \right. \kern-0pt} L} = 0. 3 5$ and ${L \mathord{\left/ {\vphantom {L D}} \right. \kern-0pt} D} = 8$, varying the second crack size ${{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } R}} \right. \kern-0pt} R}$ and location ${{L_{{{\text{c}}2}} } \mathord{\left/ {\vphantom {{L_{{{\text{c}}2}} } L}} \right. \kern-0pt} L}$. The computed results are listed in Table 2. The dimension and material properties are used same as in Sekhar [12]. Table 2 shows a good agreement which has been attained, thus validating the multiple cracks formulation.

Table 2 Variation of fundamental frequencies with ${{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } R}} \right. \kern-0pt} R}$ and ${{L_{{{\text{c}}2}} } \mathord{\left/ {\vphantom {{L_{{{\text{c}}2}} } L}} \right. \kern-0pt} L}$

4.1 Material Properties Variation for an FG Shaft

The variations of temperature-dependent properties $E{\text{ and }}\nu$ along the radial distance of the FG (SS/ZrO₂) shaft for different values of $k$ are shown in Fig. 2a, b, following power law distribution and using Eq. (2).

Fig. 2

Variation of a Young’s modulus and b Poisson’s ratio, as functions of y, k and $\Delta T$

4.2 LFCs Variation

Using Eq. (6) along with Eq. (2) and uniform temperature distribution (i.e., $T = T_{\text{o}}$ at all $y$), LFCs are obtained as non-dimensional quantities such as $\overline{C}_{11} = C_{11} /\pi E_{\text{ss}} R,\,\overline{\,C}_{22} = C_{22} /\pi E_{\text{ss}} R$, $\overline{C}_{33} = C_{33} /\pi E_{\text{ss}} R^{3} ,$ $\overline{C}_{34} = C_{34} /\pi E_{\text{ss}} R^{3}$ and $\bar{C}_{44} = C_{44} /\pi E_{\text{ss}} R^{3}$. Figure 3a shows the variation of $\overline{C}_{11}$ as functions of ${\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R}$ and $k$ for $\Delta T = 0{\text{ K}}$ and $\theta = 180^\circ$. It has been seen that the LFC increases in magnitude as $k$ decreases due to the decrease in the metallic content. Figure 3b shows the variation of $\overline{C}_{11}$ as a function of $\Delta T$ and $\theta$ for $k = 5.0{\text{ and }}{\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R} = 0.8$. With the increase in $\Delta T$, it has been seen that the LFC increases as material becomes softer. It is also noticed that the magnitude of LFC increases as the crack gradually opens. Similar kinds of trends are observed for other LFCs.

Fig. 3

Variation of $\overline{C}_{11}$: a ${\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R}$ for different k and b $\theta$ for different $\Delta {{T}}$

4.3 Importance of $\Delta T$ and $k$ on Natural Frequencies

A non-spinning simply supported cracked shaft made of FGM (${L \mathord{\left/ {\vphantom {L D}} \right. \kern-0pt} D} = 12.5$, ${{L_{\text{c}} } \mathord{\left/ {\vphantom {{L_{\text{c}} } L}} \right. \kern-0pt} L} = 0.5$, $k = 3. 0 { }$ and ${\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R} = 0.6$) is considered and dimensionless natural frequencies $\varpi_{n}$$(\varpi_{n}^{4} = {{\rho_{\text{SS}} AL^{4} \omega^{2} } \mathord{\left/ {\vphantom {{\rho_{\text{SS}} AL^{4} \omega^{2} } {E_{\text{SS}} I}}} \right. \kern-0pt} {E_{\text{SS}} I}})$ is computed for different values of $\Delta T$. Computed results are listed in Table 3 and show that for a certain ${\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R}$, $\varpi_{n}$ decreases with the increase in $\Delta T$. Table 3 also shows the reduction in $\varpi_{n}$ with $\Delta T$ which is more for lower value of $k$.

Table 3 Frequency parameters $\varpi_{n}$ of FG shaft for ${\alpha \mathord{\left/ {\vphantom {\alpha R}} \right. \kern-0pt} R} = 0.6\,\,{\text{and}}\,\,{{L_{\text{c}} } \mathord{\left/ {\vphantom {{L_{\text{c}} } L}} \right. \kern-0pt} L} = 0.5$

4.4 Influence of Material Gradient Index on Whirling Frequencies

Here, the FG shaft (${L \mathord{\left/ {\vphantom {L D}} \right. \kern-0pt} D} = 12.5$) is supported by isotropic undamped bearings with stiffness coefficients $K_{\text{vv}}^{\text{b}} = K_{\text{ww}}^{\text{b}} = 1.7513 \times 10^{7} \,{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {\text{m}}}} \right. \kern-0pt} {\text{m}}}$ and $K_{\text{vw}}^{\text{b}} = K_{\text{wv}}^{\text{b}} = 0$ for obtaining the whirling frequencies of the cracked rotor systems. Figures 4a, b show the variation of whirling frequencies $\omega$ with $\Omega$ of the uncracked FG shaft with $\Delta T = 0{\text{ K}}$ for different magnitudes of $k$. From Fig. 4a, b, it is seen that with the increase in $\Omega$, forward whirling (FW) frequencies increase while decrease the backward whirling (BW) frequencies. It is also observed that with the increase in $k$, FW and BW frequencies decreases. Therefore, for an FG shaft system, whirling frequencies are kept within a desired limit by choosing an appropriate $k$.

Fig. 4

Campbell diagram for an uncracked shaft system with k: a first mode and b second mode

4.5 Influences of $\theta$ and $\Delta T$ on Whirling Frequencies

The fundamental frequencies associated with the plane of vertical $\omega_{{ \, 1{\text{V}}}}$ and horizontal $\omega_{{ \, 1{\text{H}}}}$ are computed for two-cracked FG shaft with ${{\alpha_{1} } \mathord{\left/ {\vphantom {{\alpha_{1} } {R = {{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } R}} \right. \kern-0pt} R} = 0.8}}} \right. \kern-0pt} {R = {{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } R}} \right. \kern-0pt} R} = 0.8}},$ ${{L_{{{\text{c}}1}} } \mathord{\left/ {\vphantom {{L_{{{\text{c}}1}} } L}} \right. \kern-0pt} L} = 0.34,$ ${{L_{{{\text{c}}2}} } \mathord{\left/ {\vphantom {{L_{{{\text{c}}2}} } L}} \right. \kern-0pt} L} = 0.5$ and $\theta_{1} = 180^\circ$, while $\theta_{2}$ is varied and the influences of $\Delta T$ on the natural frequencies are carried out for ${L \mathord{\left/ {\vphantom {L D}} \right. \kern-0pt} D} = 12.5{\text{ and }}k = 5.0$. The results are presented in Fig. 5a, b which show that with the increase in $\Delta T$, % reduction in $\varpi_{1V,1H}$ decreases, and for $\theta_{1} = \theta_{2} = 180^\circ$, maximum reduction occurs. It is also seen that for lower magnitudes of $\Delta T$, % reduction in $\varpi_{1V,1H}$ will be higher even though the difference is not significant.

Fig. 5

Percentage reduction of $\varpi$ for FG cracked shaft system with $\theta_{2}$ and $\Delta T$: a $\varpi_{{1{\text{V}}}}$ and b $\varpi_{{1{\text{H}}}}$

5 Conclusions

The present work studies the eigenfrequencies analysis of a functionally graded shaft with two cracks, considering thermo-elastic material properties gradation followed by power law of material gradation law. The LFCs are evaluated using linear elastic fracture mechanics and energy method. The validations are performed in various steps using developed FE code in MATLAB, and using this developed code, the importance of size of cracks, material gradient and temperature on the computation of LFCs and eigenfrequencies is discussed. It is observed that in the case of two cracks of different depths, the larger crack has the more significant effect on the eigenfrequencies. The natural whirling frequencies decrease with increase in material gradient and temperature. However, reductions in FW and BW frequencies are greatly influenced by material gradient index. Hence, the material index could be chosen properly to design shafts made of FGMs for high-temperature applications. The present FE formulations and determination of LFCs may be helpful to the design of FG shafts following other material gradation laws such as exponential and sigmoidal.