Keywords

1 Introduction

Application of FO models is more apposite for the representation and interpretation of these real dynamical systems than its IO versions. FO-\(PI^{\lambda } D^{\mu }\) controller is therefore naturally suitable for these FO plants. They are being largely employed by many researchers in order to pull off and accomplish the most robust conduct of the plants under control [1,2,3]. Integration and derivatives with non-integer orders come into sight if the controller or the system is described by differential equations with generalized orders. The comparative study [4, 5] calls attention to the supremacy of availing these FO-\(PI^{\lambda } D^{\mu }\) controllers over traditional PID controllers with settling time and maximum peak overshoot diminished with content. To a great extent, the adjusting and regulating statutes of the numerical terms of the controllers proposed in the literature are at most applicable to self-regulating asymptotically stable processes, whereas integral processes and unstable processes have been disregarded and are not heeded to. Besides, investigation of stability of the system counteracted with the FO controller is dispensed with Riemann surface [6]. In this work, the controller parameters are selected by root locus technique with the non-integer orders graphically tuned to achieve satisfactory stability margins and sensitivity peaks. Numerical examples illustrated and explained elaborately to validate the design approach made. The results fed here entitle to express for a given process, the performance advancement, and upgrade that can be attained by bringing into utilization the FO controllers in lieu of the IO one.

2 Generalized Non-integer Order PIλDµ Controller

A PID controller is a comprehensive feedback control composition extensively and broadly exercised on industrial applications for several decades [1]. In the perpetuation of the derivative and integrator orders from integer to fractional numerals yields a better adaptable adjusting scheme of the \(PI^{\lambda } D^{\mu }\) controllers and consequently an elementary approach to achieve control requisites in contrast to its integer equivalent [2]. The control action affects the system behavior by increasing the pace of the dynamic reaction by slashing error in steady state. The command signal from the controller \(u(t)\) adapts effortlessly with the rate of change of error signal \(e(t)\) by the combination of the three continuous controller modes as [3],

$$u(t) = K_{P} e(t) + K_{I} \int\limits_{0}^{t} {e(t)dt + K_{D} } \frac{d}{dt}e(t)$$
(1)

The three adjustable control parameters here are proportional control \((K_{P} )\), integral control \((K_{I} )\), and derivative control \((K_{D} )\) gains. The control law is thus sustained in the form as [4],

$$C_{PID} (s) = K_{P} + \frac{{K_{I} }}{s} + K_{D} s$$
(2)

In complement to the typically common PID controllers, with the two ancillary variable quantities of \(PI^{\lambda } D^{\mu }\) (FOPID) controllers, it is essential to study the additional design statements that can be fulfilled as far as performance with plant uncertainties and high-frequency noise is concerned. The continuous-time transfer function representation of the generalized structure of the controller is contemplated as [5],

$$C_{{PI^{\lambda } D^{\mu } }} (s) = K_{P} + \frac{{K_{I} }}{{s^{\lambda } }} + K_{D} s^{\mu }$$
(3)

with the non-integer orders \(\lambda\) and \(\mu\) specified between the range 0 and 2 [1]. These are barely sensitive to plant uncertainties, generating vigorous performance against gain changes and noise [6].

3 Fundamental Design Philosophy

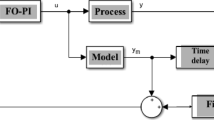
The design philosophy conceived in the available literature mostly deals with the choice of gain cross-frequency \((\omega_{cg} )\) and Phase Margin (PM). This has been feasible due to the structure of the controllers considered. However, FO-\(PI^{\lambda } D^{\mu }\) controllers, on the contrary, do not provide such opportunity to the designer. Therefore, the design philosophy adopted here according to the scheme in Fig. 1 is not the same and is quite different.

Fig. 1
figure 1

Overview of fractional order (FO) control scheme

Full size image

The following section describes a procedure which allows defining the parameters of a FO-\(PI^{\lambda } D^{\mu }\) controller. It is obvious from the formation of the PID controller in Eq. (2) that it has two zeros and one pole at the origin in the s-plane as

$$C_{PID} (s) = \frac{{K_{D} s^{2} + K_{P} s + K_{I} }}{s} = \frac{{K(s + z_{1} )(s + z_{2} )}}{s}$$
(4)

Hence, one may initiate the design with placing of these zeros simply in the LHP of the complex s-plane. Root locus analysis seems to be advantageous in this direction. Now, FO-\(PI^{\lambda } D^{\mu }\) controller does not clearly have these zeros. The zeros of this non-integer order controller does not clearly have these zeros. The zeros of the FO-\(PI^{\lambda } D^{\mu }\) controllers have the zeros shifted from this positions which lead to the change in the properties of stability, stability margins, and gain cross-over frequency. Therefore, the next step is to probe and investigate the stability margins of the compensated system with the variation of \(\lambda\) and \(\mu\) in the ranges between 0 and 2. The designer may have stability margin specifications well defined beforehand. The graphical solution of these non-integer orders \(\lambda\) and \(\mu\) of the controller with the zeros previously located completes the process of controller design and synthesis. In a design problem, one of the objectives is to keep the steady-state error to a minimum while at the same time the transient response must satisfy a certain set of performance specifications. It is therefore necessary to formulate some corrective system to drive the plant under control to meet the desired specifications. Given a plant, a set of attributes is defined to formulate a suitable controller so that the overall system converges to reach them. The design specifications to be met by the overall system merely include minimum deviation of the output from the reference input in steady state, % overshoot which depends on the damping ratio, with settling time and rise time as small as possible with stability margins in frequency domain within specified desired limits to achieve the design goals. This is basically a graphical iterative method. It tries to select the parameters of the controller so that the closed-loop poles are placed suitably in the stable half of the complex s-plane.

4 Proposed Design Algorithm

With the dynamic model of the plant known, the modulating scheme of the FO-\(PI^{\lambda } D^{\mu }\) controller can be analyzed by root locus technique. The following steps are pursued to realize the generalized compensation with two independent fractional orders of the FO controller for the system as

Step 1: Plotting the Root locus of the system along with an integrator \(\left[ {K \cdot \frac{G(s)}{s}} \right]\) for the gain \(K\) in the range, \(0 < K < \infty\).

Step 2: Selection of the two finite zeros at \(- z_{1}\) and \(- z_{2}\) to obtain the PID controller parameters leading to increase in damping with minimum percentage overshoot and settling time.

Step 3: The non-integer parameters \(\lambda\) and \(\mu\) of the FO-\(PI^{\lambda } D^{\mu }\) controller are varied and adjusted so that it is competent to reach and fulfill preferable positive Gain Margin (GM), Phase Margin (PM), and peak sensitivity margin.

Step 4: Now, on fulfilling the desired time and frequency domain criteria, the required FO-\(PI^{\lambda } D^{\mu }\) controller is obtained. Otherwise, repeating the entire algorithm described from step 1 with the new values of \(- z_{1}\) and \(- z_{2}\) until desired stability margins and sensitivity peak magnitudes are accomplished.

Step 5: Here, the three controller gains of the controller are determined as \(K = K_{D} ,K_{P} = K_{D} (z_{1} + z_{2} )\) and \(K_{I} = K_{D} (z_{1} z_{2} )\).

This leads to the determination of the controller gains utilizing where the non-integer orders of the fractional form are varied to attain the required stability margins. The parameters of the PID controllers are optimal in terms of frequency domain objectives adopted with desirable stability margins and sensitivity peak magnitudes to achieve satisfactory robust stabilization, with fast speed of response along with the achievement of control inputs within restricted limits. Thus, the numerical terms of the PID controller will be employed here as a part of the retuning procedure of the FO-\(PI^{\lambda } D^{\mu }\) controller illustrated through examples. The rationale behind taking up this particular method is its simplicity with satisfying more design specifications resulting in remarkable up-gradation in control quality and execution.

5 Numerical Examples with Results

Example 1

The following unstable plant with a pair of RHP pole at \(\pm 46.67\) has been considered [7] as

$$G(s) = \frac{ - 3518.85}{{s^{2} - 2177.8}}$$
(5)

to verify the proposed root locus method of formulating the FO-\(PI^{\lambda } D^{\mu }\) controller for this case. The design objectives to be met to determine the controller parameters are defined to be (a) Damping ratio,\(\xi \le 0.9\), (b) Settling Time within 1 s, and (c) Maximum percentage Peak Overshoot within 10%. Two zeros of Eq. (4) is selected at −1 and −14 to reorient the root locus path from the unstable region of the complex s-plane due to the unstable location of the RHP poles to the left half of the stable region as shown in Fig. 2a. The non-integer orders of the proposed FO-\(PI^{\lambda } D^{\mu }\) controller in the form of Eq. (3) is then varied and adjusted between 0 and 2 [4] to achieve the desirable positive GM, PM, and maximal magnitude of sensitivity tuned graphically as exhibited in Fig. 3a, b, and c. The FO-\(PI^{\lambda } D^{\mu }\) controller thus takes the form as

Fig. 2
figure 2

a Root locus plot of the compensated plant and b Variation of magnitude and phase with frequency for the FO controller

Full size image
Fig. 3
figure 3

Variation of a GM (dB). b PM(deg). c Maximum Sensitivity with the fractional orders \(\lambda\) and \(\mu\). d Response of the plant to unit step input

Full size image
$$C_{{PI^{\lambda } D^{\mu } }} (s) = 15 + \frac{15}{{s^{1.2} }} + s^{0.98}$$
(6)

The variation of the magnitude and phase of the loop transfer function with the plant in Eq. (5) and the FO controller in Eq. (6) reveals PM = \(90^\circ\) at \(\omega_{cg}\) of 3100 rad/s in Fig. 2b. in juxtapose to the IO controller which has a PM of only \(85^\circ\) at \(\omega_{cg}\) of 3000 rad/s with same controller gains. The corresponding step response is also compared in Fig. 3d. The sensitivity plot with the FO-\(PI^{\lambda } D^{\mu }\) controller confirmed to be maintained, \(\left| S \right|_{\hbox{max} } < 2\). The time domain interpretation of the transient response of the unstable plant with the integer and non-integer controllers has been summarized in Table 1.

Table 1 Comparative attributes of the FO controller with IO controller
Full size table

The closed-loop characteristic equation obtained by implementing the FO-\(PI^{\lambda } D^{\mu }\) controller in Eq. (6) is

$$s^{3.2} + 3518.8s^{2.18} + 50605s^{1.2} + 52783 = 0$$
(7)

The above equation in (7) can be transformed to the \(w\)-plane by \(w = s^{1/m}\) [6]. Here, \(m = 100\) indicates the quantity of sheets within the Riemann Surface (Fig. 4a).

Fig. 4
figure 4

a Riemann surface of function \(w = s^{1/100}\) with \(m = 100\) Riemann sheets. b Closed-loop pole locations in complex \(w\)-plane

Full size image
$$w^{320} + 3518.8w^{218} + 50605w^{120} + 52783 = 0$$
(8)

The stable region in the \(s\)-plane, \(\phi_{s} > \frac{\pi }{2}\) transforms to the sector in \(\phi_{w} > \frac{\pi }{2m}\) in \(w\)-plane [8]. Stability is confirmed if the principle sheet poles in \(w\)-plane lie within this segment. The closed-loop poles of the above Eq. (8) in the principle Riemann Sheet are \(- 1.0828\, \pm\, 0.0334i\) and \(- 1.0005\, \pm\,0.0258i\) which has arguments \(\left| {\varphi_{w1} } \right|\) = 0.0308 and \(\left| {\varphi_{w2} } \right|\) =  0.0258, both of which are \(> \frac{\pi }{2m}\) [6, 8]. It is clearly noticed from diagram in Fig. 4b that absence of poles lying within the unstable segment or sector \(- \frac{\pi }{m} < \varphi_{w} < \frac{\pi }{m}\) confirms that the arguments have \(\left| {\varphi_{w} } \right| > \frac{\pi }{2m}\) which reasserts stability.

Example 2

A Type-0 plant of a DC motor servo system with delay time is considered as [2]

$$G(s) = \frac{166.1038}{0.75507s + 1}e^{ - 0.1s}$$
(9)

Considering the undelayed dynamics of the same plant as [2]

$$G(s) = \frac{166.3714}{0.83907s + 1}$$
(10)

the FO-\(PI^{\lambda } D^{\mu }\) controller is designed to satisfy performance specifications of (a) Damping ratio,\(\xi \le 0.9\), (b) Settling Time within 5 s, and (c) Maximum percentage Peak Overshoot within 10% following the same design method put forward in Sect. 4. To satisfy these objectives, a fractional order (FO) controller of the form in Eq. (3) has been formulated in a similar way as

$$C_{{PI^{\lambda } D^{\mu } }} (s) = 0.005 + \frac{0.02}{{s^{0.8} }} + 0.0014s^{0.5}$$
(11)

The root locus of the compensated plant using the integer equivalent form of PID controller is as depicted in Fig. 5a.

Fig. 5
figure 5

a Root locus plot of the compensated plant and b Variation of magnitude and phase with frequency for the FO controller

Full size image

Utilizing the same values of the controller gains for the generalized form in Eq. (3) the non-integer orders \(\lambda\) and \(\mu\) are varied and tuned graphically in between the range 0 and 2 [4] to achieve desirable satisfactory stability margin as in Fig. 5b. Here, to select the values of the fractional orders it is observed from the plot in Fig. 6 that sensitivity peak relatively remains constant till \(\lambda = 0.9\) with the variation of \(\mu\) in the range (0.1, 1.2) beyond which it increases. It is also observed here that till this value \(\lambda\), the Phase Margin (PM) decreases drastically beyond the range \(\mu = 0.6\). With these values, the system step response has been plotted in Fig. 7a. Now, to ensure minimum % overshoot with reduced settling time the non-integer orders have been fixed up at \(\lambda = 0.8\) and \(\mu = 0.6\) to perceive the controller as in Eq. (11).

Fig. 6
figure 6

Variations of a Phase margin (PM) and b Sensitivity peak magnitude with the fractional orders \(\lambda\) and \(\mu\) of the FO controller

Full size image
Fig. 7
figure 7

a Response of the plant to unit step input and b Control signal

Full size image

The frequency response plots in Fig. 5b makes it visible that the frequency domain specification is well satisfied achieving GM \(= InfdB\) with PM \(= 76.9^\circ\) at \(\omega_{cg} = 2.26\,{\text{rad/s}}\) in contrast to the PID controller which could ascertain PM of only \(63.2^\circ\) at \(\omega_{cg} = 1.71\;{\text{rad/s}}\) employing the same controller gains. The bandwidth is \(2\,{\text{rad/s}}\) for PID controller whereas it is spotted at \(3\;{\text{rad/s}}\) in the case of the FO \(PI^{\lambda } D^{\mu }\) controller. Practically, to have an acceptable robust design, the peak sensitivity value attained in the mid-frequency region is anticipated to be less than 2 to restrict and fulfill the GM and PM specifications satisfactorily [9, 10]. The peak magnitude of sensitivity is < 1 in the mid-frequency fragment with a very low gain \(( < < 1)\) at lower frequencies and gain reaching to unity at higher frequencies. The quantitative analysis of the system step response of the proposed controller compared with its classical counterpart is tabulated in Table 2. It is noted here from Fig. 7b that the amplitude of the control signal is diminished in case of the \(PI^{\lambda } D^{\mu }\) controller with reduced settling time and % overshoot in collation with the IO-PID controller. The stability analysis can be confirmed in a similar way as in Example 1.

Table 2 Comparative attributes of the FO controller with IO controller
Full size table

Now, since, it has been verified that the loop transfer function yields a delay margin \(\tau_{d} = 0.595s\) calculated mathematically by \(\tau = (\pi \times PM)/(180 \times \omega_{cg} )\) which has led to determination of the delay margin through simulation to be 0.45 s much greater than the predefined value of 0.1 s in Eq. (9). The nominal step response and the reaction of the plant with dead-time are displayed through Fig. 8.

Fig. 8
figure 8

Step response with and without time delay

Full size image

6 Concluding Remarks

FO-\(PI^{\lambda } D^{\mu }\) controller is conveyed here for unstable and time-delayed plants. The controller parameters are selected by root locus technique with the non-integer orders graphically tuned to achieve satisfactory stability margins and sensitivity peaks. The advancement in the behavior of the system shown by availing the FO controller has been enumerated by numerical examples, stability of which is ratified by Riemann analysis. An adequate delay margin compensation for time-delayed plants is shown to accommodate the dead-time keeping hold of stability.