Ghost Fluid Lattice Boltzmann Methods for Complex Geometries

Abstract

Lattice Boltzmann method (LBM) is a widely recognized alternate numerical approach to simulate flow dynamics. In the conventional approach, the Navier–Stokes equations (conservation of mass, momentum and energy) are solved to obtain velocity, pressure and temperature fields. In LBM, on the other hand, the reduced version of the microscopic Boltzmann kinetic equations is solved numerically to determine particle distribution functions, which are then averaged to obtain macroscopic variables. Accurate enforcement of non-conforming and/or moving boundary conditions has been a challenge for LBM because the primary solution variables (particle distribution functions) are not the macroscopic variables on which boundary conditions are typically imposed. While macroscopic variables can be obtained from the particle distribution functions by weighted averaging, the reverse process is not as straightforward. Several researchers have developed strategies to accurately enforce boundary conditions. In this chapter, we first present an overview of the boundary issues in LBM and various approaches that have been developed to resolve them. We then discuss the implementation of immersed boundary method (IBM) on LBM, with particular emphasis on the ghost fluid approach. This technique based on ghost cells was first introduced to LBM by Tiwari and Vanka (Int J Numer Methods Fluids 69(2):481–498, 2012), who developed the so-called ghost fluid immersed boundary lattice Boltzmann method (GF-IB-LBM) based on extrapolation of particle distribution functions. The method is simple and efficient and is applicable to general boundary conditions. Another key advantage is the strict imposition of hydrodynamic conditions at the boundaries. Additionally, the method is local, thus maintains high parallelism of LBM. The application of this approach on several problems is discussed here, including its parallelization using graphical processing units (GPUs), and its coupling with molecular dynamics (MD) simulations. The chapter ends with a brief discussion on recent advances in this approach.

1 Lattice Boltzmann Method

Lattice Boltzmann method (LBM) (Chen and Doolen 1998; Luo 2000) has emerged as a powerful alternate computational tool for simulating microscopic and macroscopic flows in complex configurations. In conventional computational fluid dynamics (CFD) methods, the Navier–Stokes equations describing the continuum behavior of fluid flows are solved numerically. The equations describing the conservation of mass, momentum and energy are solved to determine the macroscopic variables (velocity, pressure and temperature). On the other hand, LBM is a meso-scale method which solves reduced versions of the microscopic Boltzmann kinetic equations for particle distribution functions. Simplified kinetic models are developed that retain only specific details of the molecular motion sufficient to recover macroscopic hydrodynamic behavior. LBM is, therefore, an intermediate approach between the continuum and the more fundamental approach of molecular dynamics (MD) simulations.

LBM evolved from lattice gas automata (LGA), in which a simplified kinetic model is constructed for simulating fictitious particles in discrete lattice space and time. The LGA model proposed by Frisch et al. (1986) consists of a two-dimensional equilateral triangular lattice space with hexagonal symmetry. Particles point toward the nearest lattice site; the kinetic model consists of collision and streaming based on certain rules. LGA is based on Boolean operation, thus suffers from statistical noise. This problem was cured by replacing Boolean particle distribution variables with ensemble-averaged particle distribution functions (McNamara and Zanetti 1988), which formed the basis of LBM. However, the primitive formulations of LBM were computationally inefficient because of the complexity of the collision operator in the ensemble form. The major breakthrough in efficiency was achieved through the linearization of the collision operator (Higuera and Jiménez 1989) assuming local equilibrium. This was further simplified using the Bhatnagar–Gross–Krook (BGK) approximation (Bhatnagar et al. 1954) of single relaxation time toward equilibrium leading to the lattice Bhatnagar–Gross–Krook (LBGK) model; the local equilibrium functions are chosen such that macroscopic equations are recovered (Qian et al. 1992; Chen et al. 1992).

Since LBM is an intermediate approach between the macroscopic and microscopic methods, the Navier–Stokes equations can be obtained by carrying out multi-scale expansion of the LB equations (Chen and Doolen 1998; Luo 2000). Similarly, LB equations can be derived from the continuum Boltzmann BGK equations, in which the equilibrium distribution is described by the Boltzmann–Maxwellian function. Low Mach number reduction of Boltzmann BGK equations leads to LB equations (Chen and Doolen 1998; Luo 2000). There is an extensive literature on analysis and advancement of LBM for various applications.

Fig. 6.1

D2Q9 model of LBM

1.1 Basic Formulation of LBM

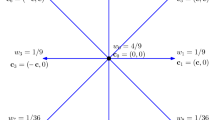
In LBM, particle distribution functions are advanced in time via two processes: collision and streaming. Various advanced formulations have been developed over the years for these processes (e.g., multi-relaxation-time LBM and entropic LBM). However, since the focus of this book in on boundary conditions, for conciseness, we present a widely used basic formulation of LBM here—the single relaxation-time D2Q9 model. As the name suggests, it is a two-dimensional model, in which the collision process employs a single relaxation-time parameter, and particles are restricted to move along nine velocity vectors during streaming, as shown in Fig. 6.1 (see Sect. 6.4.3 for a three-dimensional LBM implementation). The discrete equation governing these processes is

$$\begin{aligned} f_i(\mathbf {x}+c\,\mathbf {v}_i\Delta t, t+\Delta t) - f_i(\mathbf {x},t) = - \Omega _i, \quad i = 0,1,\dots , 8, \end{aligned}$$

(6.1)

in which, the left- and right-hand sides represent streaming and collision processes, respectively. $f_i$ is the discrete particle distribution function, $\mathbf {x}$ is the spatial location vector, $\mathbf {v}_i$ is the particle velocity, t is time and $\Delta t$ is the time step. $c=\Delta x/\Delta t$ is the lattice speed, where $\Delta x$ is the lattice spacing. $\Omega _i$ denotes discrete collision operation. The nine velocities are given by

$$\begin{aligned} \mathbf {v}_i = {\left\{ \begin{array}{ll} (0,0) &{} \text {for }i = 0, \\ (\cos ((i-1)\pi /2),\,\sin ((i-1)\pi /2)) &{} \text {for }i = \text {1 to 4}, \\ \sqrt{2}(\cos ((i-5)\pi /2+\pi /4),\,\sin ((i-5)\pi /2+\pi /4)) &{} \text {for }i = \text {5 to 8}. \end{array}\right. } \end{aligned}$$

(6.2)

The collision term $\Omega _i$ can take various forms provided the conservation laws are obeyed; the linearized collision function based on BGK approximation takes the form

$$\begin{aligned} \Omega _i = \frac{f_i - f_i^{\text {eq}}}{\tau }, \end{aligned}$$

(6.3)

where $\tau$ is a relaxation-time parameter, and $f_i^{\text {eq}}$ is the equilibrium particle distribution function:

$$\begin{aligned} f_i^{\text {eq}}=w_i \rho \left( 1+\frac{c\,\mathbf {v}_i \cdot \mathbf {u}}{c_s^2} + \frac{(c\,\mathbf {v}_i \cdot \mathbf {u})^2}{2c_s^4} - \frac{\mathbf {u}^2}{2c_s^2}\right) , \end{aligned}$$

(6.4)

where $c_s=c/\sqrt{3}$ is the lattice speed of sound and $w_i$ is the weighing function:

$$\begin{aligned} w_i = {\left\{ \begin{array}{ll} 4/9 &{} \text {for }i = 0, \\ 1/9 &{} \text {for }i = \text {1 to 4}, \\ 1/36 &{} \text {for }i = \text {5 to 8}. \end{array}\right. } \end{aligned}$$

(6.5)

$\rho$ and $\mathbf {u}$ are the density and flow velocity, respectively, obtained from the particle distribution functions and velocities using

$$\begin{aligned} \rho = \sum {f_i}\text { and }\rho \, \mathbf {u}= \sum {c\,f_i \,\mathbf {v}_i}. \end{aligned}$$

(6.6)

Applying a Chapman–Enskog procedure on the LB equations, macroscopic continuity and momentum equations can be derived in the low Mach number limit, with pressure (p) and kinematic viscosity ($\nu$) given by $p=\rho \,c_s^2$ and $\nu =(\tau -1/2)\,c_s^2\,\Delta t$.

1.2 Advantages of LBM

LBM offers a number of advantages compared to the conventional CFD methods. The simplified kinetic model utilized in LBM has a linear streaming operator, while Navier–Stokes equations have a nonlinear convection term. The nonlinearity associated with the collision operator in LBM is localized, which makes it highly suited for parallelization (see Sect. 6.4.4 for a discussion on parallelization using GPUs). In LBM, pressure variations are implicitly expressed as a function of density variations, thus eliminating the well-known pressure–velocity coupling issue that needs special treatment in conventional incompressible CFD solvers. Furthermore, since LB equations are obtained by reducing Boltzmann equations, (1) micro-scale multi-phase physics are easier to incorporate in LBM and (2) coupling with molecular dynamics (MD) simulations is straightforward (discussed in Sect. 6.4.5). It is thus widely used in the analysis of complex fluids and multi-phase flows. Conventional solvers need special care in dealing with multi-phase flows (Shukla et al. 2010; Tiwari et al. 2013). LBM also offers advantages compared to molecular simulations. In LBM, the simplified kinetic model utilizes a small set of velocities in the phase space. This makes computations significantly faster compared to solving the Boltzmann equations of molecular motion derived from the kinetic theory utilizing the Boltzmann–Maxwellian equilibrium distribution function, where the phase space is continuous and infinite.

2 Boundary Conditions in LBM

Accurate implementation of boundary conditions is challenging in LBM due to the difficulty in obtaining particle distribution functions from the prescribed hydrodynamic conditions at the boundaries. This is because the number of unknown particle distribution functions is typically more than the number of hydrodynamic boundary conditions. For stationary walls, the basic implementation of the well-known bounce-back condition simply inverts the particle velocities at the wall. However, it is only first-order accurate, and not applicable to moving walls. Several advancements have been proposed to improve its applicability and accuracy (Ziegler 1993; Ladd 1994; Filippova and Hänel 1998; Mei et al. 1999; Ginzburg and d’Humieres 2003; Lallemand and Luo 2003; Yu et al. 2003).

In the so-called hydrodynamic boundary implementation (Noble et al. 1995), the unknown (incoming) particle distribution functions are obtained from the prescribed hydrodynamic conditions at the boundaries using Eq. (6.6). The original implementation was only limited to those LBM models in which the number of unknown distribution functions is equal to the number of hydrodynamic boundary conditions. This limitation was addressed later by proposing additional rules to handle LBM models in which the number of missing functions is more than the prescribed boundary conditions (Maier et al. 1996; Zou and He 1997). Chen et al. (1996) proposed an extrapolation approach, in which the incoming distribution functions are extrapolated from the interior distribution functions, and the equilibrium distribution functions at the boundaries are computed from the prescribed hydrodynamic boundary conditions using Eq. (6.4). Guo et al. (2002) developed an extension of this method by splitting the incoming distribution functions into equilibrium and non-equilibrium parts. Equilibrium parts are computed using Eq. (6.4), while the non-equilibrium parts are extrapolated from the interior functions.

All the boundary approaches mentioned above need special care when dealing with complex geometries. For conventional CFD methods, immersed boundary methods (IBM) are now widely used to deal with curved boundaries. Since its first introduction by Peskin (1972), there has been an extensive amount of research on IBM. Among the approaches developed are forcing via deformation of elastic region tracked by Lagrangian points (Peskin 1972; Goldstein et al. 1993; Lai and Peskin 2000; Lee and LeVeque 2003), forcing via Lagrange multipliers (Glowinski et al. 1999; Taira and Colonius 2007), direct forcing by modifying discrete momentum equations (Mohd-Yusof 1997; Fadlun et al. 2000; Balaras 2004; Gilmanov and Sotiropoulos 2005; Uhlmann 2005), direct boundary implementation using Cartesian grid method (Ye et al. 1999) and direct boundary implementation using ghost cells (Majumdar et al. 2001; Tseng and Ferziger 2003). In the ghost-cell technique, hypothetical (ghost) cells are placed outside the fluid domain such that each cell has at least one neighbor inside the domain. Various options have been developed to extrapolate values to these cells to enforce boundary conditions. One widely used implementation obtains values via locating image points inside the fluid domain along the boundary normal (Majumdar et al. 2001).

IBM has been implemented into LBM as well. The original IB formulation of forcing via deformation of elastic region was coupled with LBM by Feng and Michaelides (2004). The same authors later employed direct-forcing IB formulation in LBM (Feng and Michaelides 2005). An alternative way of calculating the forcing term was developed by Niu et al. (2006) via the momentum exchange method of Ladd (1994). Several researchers have extended/improved forcing function-based IBM for various applications (Peng et al. 2006; Zhang et al. 2007; Dupuis et al. 2008; Tian et al. 2011; Kang and Hassan 2011). A drawback of this approach is that the no-slip condition is not strictly enforced at the walls. Wu and Shu (2009) proposed a velocity correction method to solve this issue. Another way of implementing strict boundary conditions is using the ghost cells-based IB method. Tiwari and Vanka (2012) first coupled this method with LBM and demonstrated its efficiency, accuracy, generality and ease of implementation. This approach and the subsequent research works toward its applications and improvements are discussed in the following sections.

3 Ghost Fluid LBM

Here, we describe a ghost fluid immersed boundary lattice Boltzmann method (GF-IB-LBM) developed by Tiwari and Vanka (2012), which imposes hydrodynamic boundary conditions via ghost nodes, rather than using the forcing concept. A general approach using extrapolation along boundary normal is employed to obtain hydrodynamic values at the ghost nodes, which are then used to obtain equilibrium particle distribution functions. The non-equilibrium particle distribution functions are simply extrapolated from the fluid domain. The two contributions are then added to obtain particle distribution functions at the ghost nodes.

Fig. 6.2

Interpolation at image points: a all neighboring nodes inside, and b two inside and two outside nodes (Tiwari and Vanka 2012)

3.1 Algorithm and Implementation

For conciseness, we restrict our focus to wall (stationary as well as moving) boundary conditions in curved geometries. (The method detailed below can be extended to other types of boundary conditions in a straightforward fashion). The implementation in two dimensions (see Sect. 6.4.3 for three-dimensional extension) briefly involves the following steps.

• 1. Ghost node and corresponding image point identification: Before streaming operation, ghost nodes adjacent to a boundary are identified such that each ghost node has at least one neighboring node in the fluid domain. For each ghost node, an image point is located inside the fluid domain along the boundary normal. This is shown in Fig. 6.2.

• 2. Density and velocity determination at image points: A special bilinear interpolation procedure is developed by Tiwari and Vanka (2012) to obtain hydrodynamic values at the image points. A four-point interpolation is used when all the surrounding nodes are interior (Fig. 6.2a). If a surrounding node is not interior (Fig. 6.2b), then it is replaced by the point of intersection of the normal from that node with the boundary curve. For velocity, the values at the wall intersection points are simply the prescribed boundary values. These points are used along with the interior nodes to obtain velocities at image points. This approach to obtain bilinear coefficients can be expressed using this general formula:

  $$\begin{aligned}&a\,x_j + b\, y_j + c\,x_j\, y_j + d=\mathbf {u}_j \quad \text {if node}\,j\, \text {is inside},\\&a\,x^{\prime }_j + b\, y^{\prime }_j + c\,x^{\prime }_j\, y^{\prime }_j + d=\mathbf {u}^{\prime }_j \quad \text {otherwise}, \end{aligned}$$

  where $j=1{:}4$ denote the four surrounding nodes, a to d are the bilinear coefficients, $(x_j,\,y_j)$ and $\mathbf {u}_j$ are the spatial Cartesian coordinates and velocity, respectively, at node j and $(x^{\prime }_j,\,y^{\prime }_j)$ and $\mathbf {u^{\prime }}_j$ are the spatial Cartesian coordinates and velocity, respectively, at the wall intersection point of node j. For density, the interpolation formula is modified such that it utilizes the zero normal gradient condition at the wall intersection points. This can also be expressed using this general formula:

  $$ \begin{array}{ll} a\,x_j + b\, y_j + c\,x_j\, y_j + d=\rho _j &{}\quad \text {if node}\, j\, \text {is inside},\\ a\,n_{xj} + b\, n_{yj} + c\,(x_j\,n_{yj}+y_j\,n_{xj}) =0 &{}\quad \text {otherwise}, \end{array} $$

  where $(n_{xj},\,n_{yj})$ denotes the boundary normal from node j, and $\rho _j$ is the density at node j.

• 3. Density and velocity determination at ghost nodes: Velocity and density values at the image points are extrapolated to the ghost points along the normal direction such that the prescribed velocity and zero density gradient conditions are satisfied at the wall.

• 4. Particle distribution function determination at ghost nodes: The equilibrium part ($f_i^{\text {eq}}$) is obtained from density and velocity values at the ghost nodes using Eq. (6.4). The non-equilibrium part ($f_i^{\text {neq}}=f_i-f_i^{\text {eq}}$) is obtained analogous to density computation using the aforementioned special interpolation procedure. The two contributions are then summed to obtain particle distribution functions at the ghost nodes, which are then streamed inside the fluid domain during streaming operation. Note that second-order accuracy of the equilibrium part is ensured by the second-order accurate bilinear interpolation of density and velocity. However, the simple extrapolation of non-equilibrium part is only first-order accurate. Overall, second-order accuracy is attained because the non-equilibrium part corresponds to the first-order term in the asymptotic expansion of the particle distribution functions (Tiwari and Vanka 2012; demonstrated in Sects. 6.4.1 and 6.4.2).

3.2 Advantages

The overall approach is simple and efficient and preserves second-order accuracy for curved boundaries. A major advantage is its generality—applicable to inflow/outflow, moving wall, symmetric and periodic boundary conditions (including Dirichlet as well as Neumann conditions; Tiwari and Vanka 2012). An illustration is presented in Sect. 6.4.2. Furthermore, the method by design imposes hydrodynamics conditions strictly at the boundaries. Boundary enforcement is local, hence preserves high parallelism of LBM (discussed in Sect. 6.4.4). It also enables straightforward coupling with molecular dynamics simulations via ghost nodes, as demonstrated in Sect. 6.4.5.

4 Application of GF-IB-LBM

We first demonstrate the accuracy of GF-IB-LBM on four test problems involving curved and moving boundaries. Then, we discuss its coupling with molecular dynamics in a GPU-parallelized framework. For conciseness, only key results are presented here; we refer to Tiwari and Vanka (2012), Tiwari et al. (2009) and Marsh (2010) for more details.

4.1 One-Dimensional Problem

We first consider cylindrical Couette flow problem to (1) compare results with analytical solution and (2) demonstrate the importance of extrapolation of non-equilibrium distribution function in achieving second-order accuracy. The flow is assumed laminar, which makes this problem inherently one dimensional, which we solve using a two-dimensional lattice for demonstration (Tiwari and Vanka 2012). We consider an inner cylinder of radius $r_1$ rotating with an angular velocity $\omega$ and a stationary outer cylinder of radius $r_2$. Angular velocity is chosen such that Reynolds number based on the inner cylinder’s diameter and tangential speed is 50. Figure 6.3 shows good agreement of velocity (u) variation along the radial (r) direction with the analytical solution. In Fig. 6.4a, the $L_2$ error norm ($\left\| e \right\| _N$) of velocity along the radial direction is plotted against grid spacing to demonstrate second-order accuracy of the method. We also plot in Fig. 6.4b, the results obtained without extrapolating the non-equilibrium part ($f_i^{\text {neq}}$), which shows a $\text {slope}\approx 1.4$. This demonstrates the importance of extrapolation of the non-equilibrium part.

Fig. 6.3

Comparison of radial velocity profile for cylindrical Couette flow using a $321\times 321$ grid in a $2.5 r_2\times 2.5 r_2$ square domain with analytical solution for two aspect ratios ($A=(r_2-r_1)/r_1$) (Tiwari and Vanka 2012)

Fig. 6.4

Variation of $L_2$ error norm ($\left\| e \right\| _N$) of radial velocity with grid spacing ($\Delta x$) for cylindrical Couette flow for two aspect ratios ($A=(r_2-r_1)/r_1$); m denotes slope (Tiwari and Vanka 2012)

Fig. 6.5

Schematic of the domain considered and variation of $L_2$ error norm ($\left\| e \right\| _N$) of radial velocity with grid spacing ($\Delta x$) for two cases of flow between rotating eccentric cylinders: case 1 has inner cylinder rotating and case 2 has outer cylinder rotating; m denotes slope (Tiwari and Vanka 2012)

4.2 Two-Dimensional Problems

We next consider flow between two rotating eccentric cylinders (Fig. 6.5a). Due to a misalignment in their rotation axes, the flow between them is two dimensional. This configuration is included here to show second-order accuracy of GF-IB-LBM for a two-dimensional problem. Tiwari and Vanka (2012) considered four different combinations of eccentricity, radius ratio and rotational speeds. For conciseness, we present here grid convergence of two cases: (1) inner cylinder rotating and (2) outer cylinder rotating. Figure 6.5b demonstrates second-order accuracy of the method.

Fig. 6.6

Streamlines in the recirculation zone and variation of pressure coefficient with cylinder angle for flow over a cylinder using GF-IB-LBM with $n=64$ (Tiwari and Vanka 2012)

Table 6.1 Comparison of drag and lift coefficients (Tiwari and Vanka 2012) with Schäfer et al. (1996)

We next consider flow over a cylinder in a channel. The previous two problems had only wall boundaries, therefore, this problem is chosen to demonstrate generality of the method for other types of boundary conditions. In this problem, parabolic velocity boundary condition is applied at the inlet, and constant pressure as well as fully developed conditions are separately considered at the outlet (Tiwari and Vanka 2012). This is a widely used verification problem; extensive benchmarking data exists (Schäfer et al. 1996). Reynolds number based on average inlet velocity and cylinder diameter is 20 for the simulated configuration. We consider three uniformly spaced lattices with $n=16$, 32 and 64, where n denotes the number of nodes across the diameter. Figure 6.6a shows streamlines in the recirculation zone, and Fig. 6.6b shows variation of pressure coefficient $c_p$ with cylinder angle $\theta$ using GF-IB-LBM ($n=64$) with constant pressure boundary condition at the outlet. The drag and lift coefficients compare well with those reported by the high-resolution study of Schäfer et al. (1996) in Table 6.1.

Fig. 6.7

Schematic, velocity vectors and contours of horizontal velocity component obtained by simulating Taylor–Couette problem using three-dimensional GF-IB-LBM (Tiwari et al. 2009)

4.3 Three-Dimensional Problem

We demonstrate the extension of the approach to three dimensions in this section. Single relaxation-time D3Q27 LBM model is used here. As the name suggests, it consists of a three-dimensional lattice with particles restricted to move along 27 directions. The ghost fluid technique described in Sect. 6.3 is extended to three dimensions via tri-linear interpolation. In this case, an image point is surrounded by eight neighboring nodes; during interpolation, the outside nodes are replaced with the intersection of normal from those nodes with the boundary, analogous to the two-dimensional implementation. For demonstration, we simulate Taylor–Couette flow between cylinders (Fig. 6.7) using this approach (Tiwari et al. 2009). We consider the following configuration: radius ratio (inner radius/outer radius) is 0.5 and aspect ratio (height/inner radius) is 3.8. Rotational speed is chosen such that the Reynolds number based on the gap between the annulus and the tangential speed is 100. The generation of toroidal vortices due to flow instability at high Reynolds number is well known and widely studied (Wereley and Lueptow 1998) for the Taylor–Couette problem. Tiwari et al. (2009) simulated this configuration using GF-IB-LBM; Fig. 6.7 shows generation of vortices with a $125\times 125\times 95$ lattice.

4.4 Parallelization Using Graphical Processors

Lattice Boltzmann method is inherently highly parallelizable, hence significant speed-up can be obtained by utilizing graphical processing units (GPUs). One of the advantages of GF-IB-LBM is that it preserves the locality of the underlying LBM model—only needs information of the nodes surrounding the image points to enforce boundary conditions. Marsh (2010) developed a parallel implementation of LBM on GPUs and highlighted that parallelization of the ghost fluid technique was straightforward. They used Compute Unified Device Architecture (CUDA) (NVIDIA: https://developer.nvidia.com/cuda-zone), which is the melding of hardware and software that NVIDIA has provided to allow scientific applications to be more easily written and executed on an NVIDIA GPU. CUDA operates by executing threads on multiprocessors contained within the GPU. They reported 50–75 times speed-up on a modern GPU compared to a modern central processing unit (CPU) for their test problems using GF-IB-LBM.

4.5 Coupling with Molecular Dynamics

We next discuss the applicability of ghost fluid method in coupling LBM with molecular dynamics (MD) simulations. MD is an atomistic method, which has been used in computational studies for a long time, but has only recently become feasible for many applications due to its high computational cost. One of the target areas of MD simulations is nano- and micro-scale flows, where the flow behavior is not well described by the Navier–Stokes equations. MD examines physical phenomena on the atomistic scale by considering individual molecules and their interactions with each other. Extensive literature exists on interaction potentials (Allen et al. 2004); the Lennard-Jones potential is often used:

$$\begin{aligned} V_{ij}(r_{ij}) = 4\epsilon \left[ \left( \dfrac{\sigma }{r_{ij}}\right) ^{12} -\left( \dfrac{\sigma }{r_{ij}}\right) ^6\right] , \end{aligned}$$

(6.7)

where $V_{ij}$ and $r_{ij}$ are the potential and distance, respectively, between molecules i and j. The two parameters $\epsilon$ and $\sigma$ are used to characterize the interaction strength and length scale, respectively.

Fig. 6.8

Schematic of LBM-MD coupling in a planar channel (Marsh 2010)

Fig. 6.9

Velocity halfway through channel flow in the overlap region (Marsh 2010)

Coupling molecular dynamics with a non-atomistic CFD code such as lattice Boltzmann is advantageous when boundary wall effects are important to capture at the atomistic resolution, but the computational penalty of such high fidelity in the bulk flow is not desired. For example, consider a simple two-dimensional, planar channel flow as shown in Fig. 6.8. Marsh (2010) decomposed it into three domains for coupling: an MD domain near walls, an LBM domain for bulk flow and an overlap domain. They used Schwarz alternating method (SAM) (Dolean et al. 2015) to couple the two methods. This approach decouples both time and length scales allowing for a fully hybrid scheme. LBM and MD individually solve their respective domains including the overlap region. SAM operates by first advancing LBM by one time step ($\Delta t$). Boundary conditions are then applied to the atomistic region via the overlap region. In this step, the velocity of a molecule in the overlap region is set to the fluid velocity at the nearest lattice node. MD is then advanced via multiple (p) smaller time steps ($\delta t$) such that $\Delta t = p\,\delta t$. Boundary conditions are then applied to the bulk region. GF-IB-LBM offers straightforward enforcement of boundary conditions from MD to LBM in this step. It just requires using the averaged values from MD and imposing them on the appropriate ghost nodes. Marsh (2010) developed a parallel implementation of the coupling approach on GPUs (as discussed in Sect. 6.4.4), and simulated the aforementioned channel flow configuration. For demonstration, we show in Fig. 6.9 the velocity vectors near wall obtained from the coupled simulation; we refer to Marsh (2010) for more details.

5 Recent Advances

Khazaeli et al. (2013) implemented ghost fluid technique on thermal LBM. Their approach uses interpolation–extrapolation methodology based on image points similar to Tiwari and Vanka’s (2012) GFM. Thermal LBM contains an additional distribution function for internal energy, whose values they obtain at ghost nodes analogous to the particle distribution function calculation via extrapolation from image points. They used an inverse distance-weighing approach for interpolation and demonstrated second-order accuracy for several problems with curvilinear boundaries.

Chen et al. (2013) investigated pressure oscillations that appear due to boundary implementation in LBM. Their investigation focused on the ghost fluid IB method (Tiwari and Vanka 2012), for which, they implemented a cut-cell-based weighting strategy to enforce geometric conservation to suppress these oscillations. They tested this method on four problems and demonstrated that the modified GFM reduces pressure oscillations while preserving its accuracy. Chen et al. (2014) compared different bounce-back and IB schemes and concluded that the unified-interpolation bounce-back of Yu et al. (2003), the direct-forcing approach of Kang and Hassan (2011) and the ghost fluid approach of Tiwari and Vanka (2012) are best suited for the acoustic problems they considered.

Kaneda et al. (2014) developed a multi-relaxation-time extension of the single relaxation-time GFM (Tiwari and Vanka 2012). They compared their results with the standard bounce-back scheme and confirmed that GFM has better accuracy, but found a defect in density calculation at image points. They attributed this to a larger predicted pressure and proposed an improvement by implementing a normal moment relation (the balance of centrifugal force and pressure) for the estimation of density distribution functions at the boundaries. Jahanshaloo et al.’s  (2016) review provides an overview of several approaches developed to impose boundary conditions in LBM (including thermal LBM).

Mozafari-Shamsi et al. (2016a) developed an extension of GFM (Tiwari and Vanka 2012) for thermal LBM and implemented it for Dirichlet as well as Neumann thermal boundary conditions. As mentioned earlier, thermal LBM contains an additional equation to evolve internal energy distribution functions. Internal energy distribution functions at the ghost nodes are obtained analogous to the calculation of particle distribution functions as described in Sect. 6.3; they employed GFM’s inherent feature of computing gradient of the macroscopic variables normal to the curved boundaries to formulate heat flux (Neumann) boundary conditions. In a later study, they (Mozafari-Shamsi et al. 2016b) used this GFM approach to formulate conjugate heat transfer boundary conditions at curved interfaces of two materials having different thermal properties. Boundary conditions for conjugate heat transfer are difficult to impose because heat fluxes must match in addition to imposing a common temperature value at the boundary points. Here, again, GFM’s (Tiwari and Vanka 2012) normal gradient calculation makes it suitable to enforce such interface conditions. They verified the accuracy and stability of GFM computations on three test problems and confirmed its second-order accuracy.

Li et al. (2016) developed a quadratic interpolation (QGFM) variant of bilinear interpolation GFM (BGFM) (Tiwari and Vanka 2012). They compared them with Guo et al.’s (2002) extrapolation method, linear interpolation bounce-back (LIBB) method and quadratic interpolation bounce-back (QIBB) method. They found that LIBB, QIBB, Guo et al.’s scheme and BGFM are comparable in efficiency for the problems simulated, but QGFM takes about 10% more computation time due to a larger stencil construction. As expected, they observed that quadratic interpolation schemes (QGFM and QIBB) are more accurate compared to their linear counterparts (BGFM and LIBB). However, they found that the conventional bounce-back schemes are more accurate than ghost fluid interpolation schemes for the problems studied. They also compared these techniques for boundary pressure oscillations in LBM and found that oscillations are best suppressed by Guo et al.’s scheme. The authors also studied the influence of different collision models, refilling techniques and force evaluation methods in suppressing pressure oscillations.

Xu et al. (2018) recently proposed a forcing-based IB-LBM scheme for fluid–structure interaction problems. To improve numerical stability, their scheme approximates the feedback coefficient explicitly and splits Lagrangian force into traction from surrounding flow and inertial force from boundary acceleration. They also developed a dynamic geometry-adaptive grid refinement strategy, which improves the efficiency of the coupled solution by having fine resolution only near the fluid–structure interfaces.