Keywords

1 Introduction

The global navigation satellite system (GNSS) has entered the multi-system and multi-frequency era. In order to make full use of the observations at each frequency, the uncombined (UC) observation model, i.e. the raw GNSS observation equation is used and no linear combination is processed, has attracted more and more attention. The UC strategy facilitates the unification of observation models, and is suitable for low-cost single-frequency applications, high-precision multi-frequency applications with the strong scalability. Keshi et al. [1] first studied the observation model of the UC strategy, and pointed out that the ionospheric-free (IF) combination ignored time-varying characteristics of the ionospheric delay. Zhang [2] compared the advantages and disadvantages of the two strategies of IF and UC in detail, and verified the positioning performance. Li [3] studied the real-time precise positioning method based on UC strategy and fixed the ambiguity. Schönemann et al. [4] showed that the difference or linear combination of observations would cause information loss. In recent years, the research on UC observational models has been deepened and applied more widely. Gu et al. [5, 6] used a UC observation model to fix the ambiguity and model the ionospheric delay. Li et al. [7] and Xiao et al. [8] analyzed the three-frequency ambiguity fixing method of UC model. When using three linear combinations for calculating fractional code bias (FCB), they used UC float ambiguities to derive the wide-lane ambiguity, rather than MW combination observations.

For UC precise orbit determination (POD), Strasser et al. [9] used UC strategy to evaluate GPS orbital accuracy during the period of 2003–2017. Results showed that comparable products accuracy was derived comparing to other analysis centres. Zeng et al. [10] proposed a UC POD method to improve the computational efficiency for the problem of huge ionospheric parameters.

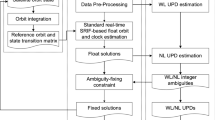
This study proposes a new method to derive WL ambiguity. The observation model of satellite precise orbit determination is given first, then a new ambiguity fixation strategy is introduced. The new method is verified, and following that is the conclusion. The work is carried out based on the software of satellite positioning and orbit determination system (SPODS) [11].

2 Methodology

The observations model is first given and then the ambiguity resolution method is described.

2.1 Satellite Precise Orbit Determination Model

Assume that the ground station r receives the pseudorange P and carrier phase L of a satellite s at the frequency i. The observation equations are

$$ \left\{ {\begin{array}{*{20}l} {P_{r,i}^{s} = \rho_{r}^{s} + c\delta t_{r} - c\delta t^{s} + m_{r}^{s} T_{r} + \gamma_{i}^{{}} I_{r,1}^{s} + B_{r,i}^{{}} - B_{i}^{s} + \varepsilon_{r,i}^{s} } \hfill \\ {L_{r,i}^{s} = \lambda_{i}^{{}} \varphi_{r,i}^{s} = \rho_{r}^{s} + c\delta t_{r} - c\delta t^{s} + m_{r}^{s} T_{r} - \gamma_{i} I_{r,1}^{s} { + }\lambda_{i}^{{}} (N_{r,i}^{s} + b_{r,i} - b_{i}^{s} )+ \xi_{r,i}^{s} \, } \hfill \\ \end{array} } \right. $$
(1)

where \( \rho_{r}^{s} \) the station-satellite geometric distance, \( \lambda \) the wavelength, \( \varphi \) the carrier phase measurement (in the unit of cycle), \( \delta t_{r} \) and \( \delta t^{s} \) the receiver and satellite clock offset, c the speed of light. \( T_{r} \) is the tropospheric delay mapping function from the zenith of the station to line of sight and \( I_{r,1}^{s} \) is the coefficient of the fist-order ionospheric delay for the frequency i = 1. \( B_{r,i}^{{}} \) and \( B_{i}^{s} \) is the pseudorange hardware delay for the receiver and satellite, respectively. \( b_{r,i}^{{}} \) and \( b_{i}^{s} \) is the carrier phase hardware delay for the receiver and satellite, respectively. \( N_{r,i}^{s} \) is the ambiguity. \( \varepsilon_{r,i}^{s} \) and \( \xi_{r,i}^{s} \) is the pseudorange and phase noise. It should be noted that there are still some error terms that are not listed when establishing the observation equation, including the antenna phase center error, the station zenith tropospheric dry delay, and tide correction.

Define the following formulas

$$ \left\{ {\begin{array}{*{20}l} {\alpha_{mn}^{{}} = \frac{{(f_{m}^{{}} )^{2} }}{{(f_{m}^{{}} )^{2} - (f_{n}^{{}} )^{2} }},\beta_{mn}^{{}} = - \frac{{(f_{n}^{{}} )^{2} }}{{(f_{m}^{{}} )^{2} - (f_{n}^{{}} )^{2} }}} \hfill \\ {DCB_{mn}^{s} = B_{m}^{s} - B_{n}^{s} ,DCB_{r,mn}^{{}} = B_{r,m}^{{}} - B_{r,n}^{{}} } \hfill \\ {B_{{IF_{mn} }}^{s} = \alpha_{mn}^{{}} \cdot B_{m}^{s} + \beta_{mn}^{{}} B_{n}^{s} ,B_{{r,IF_{mn} }}^{{}} = \alpha_{mn}^{{}} \cdot B_{r,m}^{{}} + \beta_{mn}^{{}} B_{r,n}^{{}} } \hfill \\ \end{array} } \right. $$
(2)

where \( m,n \) denote the frequency. The differential code bias (DCB) is in the unit of meter.

At present, the clock products released by IGS are based on the reference of dual-frequency IF code combination. Since

$$ B_{i} - B^{i} = B_{IF} - B^{IF} - \frac{{\gamma_{i} }}{{\gamma_{2} - 1}}\left( {DCB_{12} - DCB^{12} } \right) $$
(3)

Taylor series expansion of the observation equation to take the first order term, and parameter reorganization of (1) can be obtained

$$ \left\{ {\begin{array}{*{20}l} {P_{r,i}^{s} = \rho_{0} + \varvec{u}_{r}^{s} \cdot \varvec{x} + c\overline{\delta t}_{r}^{{}} - c\overline{\delta t}^{s} + m_{r}^{s} T_{r} + \gamma_{i}^{{}} \overline{I}_{r,1}^{s} + \varepsilon_{r,i}^{s} } \hfill \\ {L_{r,i}^{s} = \rho_{0} + \varvec{u}_{r}^{s} \cdot \varvec{x} + c\overline{\delta t}_{r}^{{}} - c\overline{\delta t}^{s} + m_{r}^{s} T_{r} - \gamma_{i}^{{}} \overline{I}_{r,1}^{s} + \overline{N}_{r,i}^{s} + \xi_{r,i}^{s} } \hfill \\ \end{array} } \right. $$
(4)

where

$$ \left\{ \begin{aligned} & c\overline{\delta t}_{r}^{{}} = c\delta t_{r} + B_{{r,IF_{12} }}^{{}} \\ & c\overline{\delta t}^{s} = c\delta t^{s} + B_{{IF_{12} }}^{s} \\ & \overline{I}_{r,1}^{s} = I_{r,1}^{s} { + }\beta_{12}^{{}} \left( {DCB_{r,12}^{{}} - DCB_{12}^{s} } \right) \\ & \overline{N}_{r,i}^{s} = \lambda_{i}^{{}} (N_{r,i}^{s} + b_{r,i}^{{}} - b_{i}^{s} ) { + (}B_{{IF_{12} }}^{s} - B_{{r,IF_{12} }}^{{}} ) \\ & \quad \quad + \,\gamma_{i}^{{}} \cdot \beta_{12}^{{}} \left( {DCB_{r,12}^{{}} - DCB_{12}^{s} } \right),i = 1,2 \\ \end{aligned} \right. $$
(5)

\( \rho_{0} \) the approximate geometric distance, \( \varvec{u}_{r}^{s} { = }\left[ {\begin{array}{*{20}c} {u_{x} } & {u_{y} } & {u_{z} } \\ \end{array} } \right]^{T} \) the partial derivative of the geometric distance \( \rho = \sqrt {(x^{s} - x_{r} )^{2} + (y^{s} - y_{r} )^{2} + (z^{s} - z_{r} )^{2} } \), corresponding to the station coordinate, \( \varvec{x} = \left[ {\begin{array}{*{20}c} {dx_{r} } & {dy_{r} } & {dz_{r} } \\ \end{array} } \right]^{T} \) the coordinate correction parameter. In the observation equation, the satellite position, velocity and force model parameters are omitted. It is obvious that the partial derivative is \( - u_{x} , - u_{y} , - u_{z} \) multiplying the state transition matrix to the satellite position, and multiplying the sensitivity matrix to the force model parameters.

It can be seen that after using the IF combined satellite clock datum (i.e. \( \overline{\delta t}^{s} \)), the pseudorange hardware delay is absorbed by the satellite clock, the receiver clock, the ionospheric delay and the ambiguity parameters, respectively, without need to additionally estimate the code delay parameters. There is no pseudorange delay parameter in the phase observation. In order to maintain the consistency of the clock reference and ionospheric parameters to pseudorange equation, the ambiguity parameter absorbs the code delay combination \( B_{{IF_{12} }}^{s,Q} \) and \( B_{{r,IF_{12} }}^{Q} \) from the clock and \( \gamma_{i}^{Q} \cdot \beta_{12}^{Q} \left( {DCB_{r,12}^{Q} - DCB_{12}^{s,Q} } \right) \) from the ionospheric parameter.

2.2 Traditional Ambiguity Resolution Method

Ambiguity resolution (AR) is the key problem for the GNSS precise data processing. The AR method of IF observation model for the POD is to use the double-differenced (DD) method. The baseline network is set up by using IF undifferenced (UD) float ambiguities to obtain the IF DD ambiguities, and the IF ambiguities are decomposed of WL- and NL-DD ambiguities. WL- and NL-DD ambiguities are fixed sequentially. The UD ambiguity is fixed with the DD constraint. The AR idea of UC POD is basically the same as that of the IF strategy. The difference is the ambiguity parameter contains the code combination \( \gamma_{i}^{Q} \cdot \beta_{12}^{Q} \left( {DCB_{r,12}^{Q} - DCB_{12}^{s,Q} } \right) \) from the ionospheric delay. However, it can decompose into WL and NL to fix the ambiguity, where the ionospheric-related code combination can be eliminated. Ignoring the satellite and receiver identification, the MW observation reads

$$ L_{MW} { = }\frac{1}{{f_{1} - f_{2} }}(f_{1} L_{1} - f_{2} L_{2} ) - \frac{1}{{f_{1} + f_{2} }}(f_{1} P_{1} + f_{2} P_{2} ) = \lambda_{w} N_{w} + bias $$
(6)

where \( L_{MW} \) contains the UD WL ambiguity \( N_{w} \) with the wavelength \( \lambda_{w} = c/(f_{1} - f_{2} ) \). bias contains the observations noise and multipath error. In order to reduce the effect of error item, the WL ambiguity must be averaged over a consecutive data arc. The formula is

$$ \left\{ {\begin{array}{*{20}l} {\left\langle {N_{w} } \right\rangle_{i} = \left\langle {N_{w} } \right\rangle_{i - 1} + (N_{wi} - \left\langle {N_{w} } \right\rangle_{i - 1} )/i} \hfill \\ {\sigma_{w,i} = \sqrt {\sigma_{w,i - 1}^{2} + \left[ {(N_{wi} - \left\langle {N_{w} } \right\rangle_{i - 1} )^{2} - \sigma_{w,i - 1}^{2} } \right]/i} } \hfill \\ \end{array} } \right. $$
(7)

where \( \left\langle {N_{w} } \right\rangle_{i} \) the average values of MW observations in a continuous arc, \( N_{wi} \) the WL ambiguity in the ith epoch, \( \sigma_{w,i} \) the standard derivation (STD) of WL ambiguities. Assuming that the DD operator is \( {\mathbf{d}} \), the WL DD ambiguity can be derived \( N_{(r,q),w}^{(s,l)} = {\mathbf{d}}N_{w} \), where \( r \) and \( q \) are two stations, \( s \) and \( l \) are two satellites. The probability decision function is used to calculate the rounding success rate. If it passes, the integer WL DD ambiguity value \( \hat{N}_{(r,q),w}^{(s,l)} \) is obtained.

Assuming that the ambiguity parameters of L1 and L2 frequency in the unit of meter are \( n_{r,1}^{s} \) and \( n_{r,2}^{s} \), then

$$ \left\{ {\begin{array}{*{20}c} {n_{r,1}^{s} = \frac{c}{{f_{1} }}N_{r,1}^{s} } \\ {n_{r,2}^{s} = \frac{c}{{f_{2} }}N_{r,2}^{s} } \\ \end{array} } \right. $$
(8)

Assuming NL ambiguity \( N_{r,n}^{s} = N_{r,2}^{s} \), the NL DD ambiguity \( N_{(r,q),n}^{(s,l)} \) and its STD \( \sigma_{n}^{D} \) can be expressed as

$$ \left\{ {\begin{array}{*{20}l} {N_{(r,q),n}^{(s,l)} \text{ = }\frac{{f_{1} + f_{2} }}{c}\left( {\alpha_{12} n_{(r,q),1}^{(s,l)} + \beta_{12} n_{(r,q),2}^{(s,l)} } \right) - \frac{{f_{1} }}{{f_{1} - f_{2} }}\hat{N}_{(r,q),w}^{(s,l)} } \hfill \\ {\sigma_{n}^{D} = \frac{{f_{1}^{2} }}{{c(f_{1} - f_{2} )}}\sigma_{1}^{D} + \frac{{ - f_{2}^{2} }}{{c(f_{1} - f_{2} )}}\sigma_{2}^{D} } \hfill \\ \end{array} } \right. $$
(9)

where \( \sigma_{1}^{D} \) and \( \sigma_{2}^{D} \) are the STD of DD ambiguities \( n_{(r,q),1}^{(s,l)} \) and \( n_{(r,q),2}^{(s,l)} \). Similarly, the probability decision function is used to obtain the integer value \( \hat{N}_{(r,q),n}^{(s,l)} \) of NL DD ambiguity. The fixed value of the DD ambiguity of the original frequency can be obtained.

$$ \left\{ {\begin{array}{*{20}l} {\hat{n}_{(r,q),2}^{(s,l)} \text{ = }\hat{N}_{(r,q),n}^{(s,l)} \cdot \frac{c}{{f_{2} }}} \hfill \\ {\hat{n}_{(r,q),1}^{(s,l)} = \left( {\hat{N}_{(r,q),w}^{(s,l)} + \hat{N}_{(r,q),n}^{(s,l)} } \right) \cdot \frac{c}{{f_{1} }}} \hfill \\ \end{array} } \right. $$
(10)

The fixed DD ambiguity information is constrained to the original UD observation equation, and all unknown parameters are updated to obtain the parameter estimation result of AR.

2.3 New Ambiguity Resolution Method

Different from the previous method, the new method does not need to use formulas (6)–(7), but uses UC float ambiguities to obtain WL DD ambiguities.

$$ N_{(r,q),w}^{(s,l)} = n_{(r,q),1}^{(s,l)} /\lambda_{1} - n_{(r,q),2}^{(s,l)} /\lambda_{2} $$
(11)

The following strategy is used to judge whether the ambiguity can be fixed: if \( \left| {N_{(r,q),w}^{(s,l)} - round(N_{(r,q),w}^{(s,l)} )} \right| < 0.2 \), then it is considered that the WL ambiguity can be fixed, and the rounding success rate is assumed to be 1. The integer value \( \hat{N}_{(r,q),w}^{(s,l)} = round(N_{(r,q),w}^{(s,l)} ) \) of WL DD ambiguities can be obtained. After the WL DD ambiguity is obtained, the following AR strategy is the same as Sect. 2.2.

2.4 Equivalence Proof of Two AR Methods

In order to verify the equivalence of two methods, double-difference calculations are performed for MW combination observation

$$ \begin{aligned} L_{{(r,q),\text{MW}}}^{(s,l)} & \text{ = }\frac{1}{{f_{1} - f_{2} }}(f_{1} L_{(r,q),1}^{(s,l)} - f_{2} L_{(r,q),2}^{(s,l)} ) - \frac{1}{{f_{1} + f_{2} }}(f_{1} P_{(r,q),1}^{(s,l)} + f_{2} P_{(r,q),2}^{(s,l)} ) \\ & \, = \frac{1}{{f_{1} - f_{2} }}(f_{1} n_{(r,q),1}^{(s,l)} - f_{2} n_{(r,q),2}^{(s,l)} ) \\ & \, = \frac{c}{{f_{1} - f_{2} }}(n_{(r,q),1}^{(s,l)} /\lambda_{1} - n_{(r,q),2}^{(s,l)} /\lambda_{2} ) \\ \end{aligned} $$
(12)

Since the MW combination eliminates the geometric distance and first-order term of ionospheric delay. Seeing formula (4), after using the MW linear combination, only the re-parameterized ambiguity remains

$$ L_{(r,q),MW}^{(s,l)} \text{ = }\frac{1}{{f_{1} - f_{2} }}(f_{1} n_{(r,q),1}^{(s,l)} - f_{2} n_{(r,q),2}^{(s,l)} ) = \frac{c}{{f_{1} - f_{2} }}N_{(r,q),w}^{(s,l)} $$
(13)

The above formula is equal to formula (11), which verifies that the ambiguity parameter obtained by the MW combination is consistent with UC float ambiguity parameter. The difference is mainly reflected in the way of the acquisition. The MW combination uses the original pseudorange and carrier phase observation data to obtain the WL ambiguity, while in the new method the UC float ambiguity is calculated through parameter adjustment with only high-precision carrier phase observations used. Therefore, it can be seen that the accuracy of WL ambiguity obtained from the new method should be higher.

3 Results Verification and Analysis

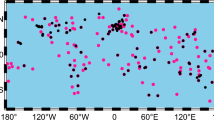
In order to verify the new method, a comparative analysis is performed from two aspects: the residual distribution of WL ambiguity and the results of POD. Since the new AR method uses 0.2 weeks as a threshold, i.e. the WL DD ambiguity with fractional part smaller than the threshold is forced to fix the integer and the rounding success rate is assumed to be 1. Therefore, whether new method is better than traditional method, which needs experimental verification. Because GPS precise products have the best products accuracy, satellite status has been solidified, and various error models are processed well, GPS satellites are selected for experimental verification. In the experiment, a total of 12 GPS BLOCK IIF satellites and about 60 IGS ground stations are used for POD. The time period is 1 to 35 days in 2018. The station distribution is shown in Fig. 1. The processing strategy of observation model and force model is shown in Table 1. The POD arc length is 1d. Three POD schemes are processed: POD with IF model (IF), POD with UC model, POD with UC model using the new AR method (UC-new).

Fig. 1.
figure 1

Ground station distribution map

Full size image
Table 1. Force model and observation model information of satellite POD
Full size table

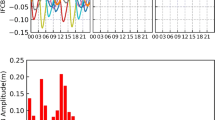
3.1 Wide Lane Residual Distribution

Figure 2 plots the residual distribution of all WL DD ambiguities derived over 35d, and Table 2 gives the percentage of each interval 0.1 cycle. Compared with the WL DD ambiguity derived using the MW strategy, the distribution of new UC method is closer to the integer value. The percentage of residuals within 0.2 weeks was 5.8% more, an increase of about 7.6%. This shows that the accuracy of the WL DD ambiguity obtained by the new method is higher than that of the MW strategy.

Fig. 2.
figure 2

Residual distribution of wide-lane double-differenced ambiguities

Full size image
Table 2. Residual statistics of wide-lane double-differenced ambiguities
Full size table

3.2 Validation of POD Results

Also use this period for processing POD, the orbit and clock results are compared to the final product of IGS, and the average value of all satellites in each arc is obtained. The orbital accuracy of GPS satellites in radial (R), tangential (T) and normal (N) direction is shown in Fig. 3. Figure 4 gives the STD and RMS of clocks. Table 3 lists the overall mean of all POD arcs. Among them, the G26 satellite is abnormal in the result of the 17th day, and the result of that day is excluded.

Fig. 3.
figure 3

Orbit comparing results of each POD arc

Full size image
Fig. 4.
figure 4

Clock comparing results of each POD arc

Full size image
Table 3. Statistics of overall orbit and clock comparing results
Full size table

From Figs. 3, 4 and Table 3:

  1. (1)

    Compared with the UC scheme, the orbit and clock accuracies of the UC-new scheme are better. The accuracy of GPS orbits is improved by about 3% in each direction. The clock STD is improved by 4.3% and the clock RMS is improved slightly.

  2. (2)

    Comparing the results of the traditional IF strategy and the UC strategy, the orbits and clocks obtained using the two observation models are basically equivalent. The UC results are slightly better than the IF results.

  3. (3)

    From the results of each POD arc, the new scheme is worse in some arcs. The possible reason is that the method of deriving the integer WL DD ambiguity needs to be improved. The strategy used in the new method is that if the fractional part of WL DD ambiguity is within 0.2 weeks, then it is regarded as a fixable ambiguity. However, the original method to derive the wide-lane double-difference ambiguity is to use MW strategy, where the rounding success rate are determined by the probability decision function according to the standard derivation of MW observations series.

4 Conclusion

This study proposes an improved AR solution of UC POD, that is, the WL DD ambiguity is derived without using the original MW observations, but using UC float ambiguities from parameter adjustment. The residual distribution of WL DD ambiguities shows that the new method has higher accuracy, with residuals less than 0.2 weeks being about 5% higher than the traditional MW method. GPS satellites are used for POD verification, with IF, UC and UC-new three schemes. Results show that the new method is slightly better than the old method, although the overall results are basically the same. The reason why the improvement is slight is that when the WL DD ambiguity is less than 0.2 weeks, it is fixed directly. The rounding success rate is assumed to be 1. The rounding strategy still needs to be improved and further research is needed.