Keywords

1 Introduction

One of the important interactions among species is the predator-prey relationship. The words “predator” and “prey” are almost always used to mean only animals that eat animals, but this idea also applies to plants. The dynamics of prey–predator has been extensively studied because of its universal existence. Several factors affecting the dynamics of predator-prey models, such a familiar factors is the functional response. The functional response is linear in the Lotka–Volterra model, which is valid first-order approximations of more general interaction.

In general, researchers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] always developed the prey–predator system with the assumption that the biological parameters are exactly known; however, the scenario is different in practical world. In reality, each of the biological parameters may not be fixed rather varying due to several reasons. Therefore, the biological parameters are very sensible and treated as nonnegative imprecise number instead of fixed real number. Peixoto et al. [21] studied predator-prey fuzzy model. Pal et al. [22] proposed optimal harvesting prey–predator bio-economic model with interval biological parameters. Pal et al. [23] presented quota harvesting model under fuzziness. In our work, we use interval approach.

This paper considers one-prey one-predator discrete system and calculates equilibrium points, stability and bifurcation of the prey–predator system, where at least one biological parameters of the model is an interval number. We present the interval parameters in the parametric function form and then study the parametric prey–predator discrete model. A parametric mathematical program is formulated to find the different behavior of the system for different value of parameter. The proposed procedure is more effective and interesting since we get different behavior of the model using functional form of an interval parameter based on interval-valued technique. The proposed procedure can present different characteristics of the model in a single framework.

The rest of the paper is organized as follows: The second section introduces mathematics for this paper. In section 3, a discrete-time prey– predator model under non-overlapping generation with refuge is formulated. Section 4 expands this model under imprecise biological parameters. Section 5 presents the local stability analysis around the interior fixed point of the proposed model. Discussion on flip bifurcation is on Sect. 6 Chaos Control procedure is given in Sect. 7. Section 8 gives a numerical simulations to support of the proposed model. Finally, this paper ends with a conclusion in Sect. 9.

2 Prerequisite Mathematics

An interval number \(A\;\)is represented by closed interval \(\left[ a_{l},a_{r}\right] \) and defined by \(A=\left[ a_{l},a_{r}\right] =\left\{ x:a_{l}\le x\le a_{r},x\in R\right\} ,\) where R is the set of real numbers and \(a_{l},a_{r}\) are the left and right limit of the interval number, respectively.

Interval-valued function: Let a, \(b>0\) and the interval \(\left[ a ,b \right] \) can represent by the interval-valued function as \(h\left( p\right) =a^{1-p}b^{p}\) for \(p\in \left[ 0, 1 \right] \).

Here, we present some arithmetic operations as follows:

Let \(A=\left[ a_{l},a_{u}\right] \) and \(B=\left[ b_{l},b_{u}\right] \) be two interval numbers.

Addition: The interval-valued function for the interval \(A+B=\left[ a_{l}+b_{l},a_{u}+b_{u}\right] ,\) provided \(a_{l}+b_{l}>0,\) is given by \(h\left( p\right) =a_{L}^{1-p}a_{U}^{p}\) where \(a_{L}=a_{l}+b_{l}\) and \(a_{U}=a_{u}+b_{u}.\)

Subtraction: The interval-valued function for the interval \(A-B=\left[ a_{l}-b_{u},a_{u}-b_{l}\right] ,\) provided \(a_{l}-b_{u}>0,\) is given by \(h\left( p\right) =b_{L}^{1-p}b_{U}^{p}\) where \(b_{L}=a_{l}-b_{u}\) and \(a_{L}=a_{u}-b_{l}.\)

Scalar Multiplication: \(\eta A=\eta \left[ a_{l},a_{u}\right] =\left\{ \begin{array}{c} \left[ \eta a_{l},\eta a_{u}\right] ; if \eta \ge 0 \\ \left[ \eta a_{u},\eta a_{l}\right] ; if \eta <0 \end{array} \right. \) 

provided \(a_{l}>0\;\)and \(b_{l}>0.\) The interval-valued function \(\eta A\) is given by \(h\left( p\right) =c_{L}^{1-p}c_{U}^{p}\) if \(\alpha \ge 0\) and \(h\left( p\right) =-d_{U}^{1-p}d_{L}^{p}\) if \(\eta <0,\) where \(c_{_{L}}=\eta a_{l},\) \(c_{_{U}}=\eta a_{u},~d_{U}=|\eta |a_{u}\;\)and \(d_{L}=|\eta |a_{l}.\)

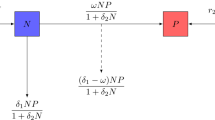
3 Description of Prey–Predator Model

We consider populations with non-overlapping generation, where all the adults die after they have given birth. General form of prey–predator system in discrete time is as follows:

$$\begin{aligned} x_{n+1}= & {} x_{n}f(x_{n},y_{n})=ax_{n}(1-x_{n})-b\sqrt{x_{n}}y_{n} \\ y_{n+1}= & {} y_{n}g(x_{n},y_{n})=c\sqrt{x_{n}}y_{n}-dy_{n} \nonumber \end{aligned}$$
(1)

where \(\frac{df}{dy_{n}}\le 0\) and \(\frac{dg}{dx_{n}}\geqslant 0.\) Here, a, b, c and d are the nonnegative model parameters. The dynamical properties of the above system allow us to get information about the long-run behavior of prey–predator populations. Starting from given initial condition \((x_{0},y_{0})\), the iteration of Eq. (1) uniquely determines a trajectory of the states of population output in the form of \((x_{n},y_{n})=T^{n}(x_{0},y_{0}),\) where \(n=0,1,2,....\)

4 Proposed Model Under Impreciseness

So far, most of the prey–predator model are considered in precise environment, but data can not be recorded or collected precisely due to several reasons in reality. Hence, analysis of the model with imprecise parameters gives better results in modeling respect. Uncertain growth rate of prey populations, interspecific competition rates of prey species, predation coefficient and reduction rates of predator species are usually considered as an effect of environmental fluctuations. Reproduction of species depends on various factors, such as temperature, parasites, pathogens, humidity and environmental pollution. Since biological environments of populations are not entirely predictable, the biological parameters of modeling of prey–predator system should be considered as imprecise in nature.

The proposed discrete-time prey–predator model is presented here with the interval coefficient due to the uncertainty of parameter of practical problem in nature.

4.1 Model with Interval Coefficient

Let \(\widehat{a},\) \(\widehat{b},\) \(\widehat{c}\) and \(\widehat{d}\) be the interval counterparts of a, b, c and d, respectively. Then, the modified model is

$$\begin{aligned} x_{n+1}= & {} \widehat{a}x_{n}(1-x_{n})-\widehat{b}\sqrt{x_{n}}y_{n} \\ y_{n+1}= & {} \widehat{c}\sqrt{x_{n}}y_{n}-\widehat{d}y_{n} \nonumber \end{aligned}$$
(2)

where \(\widehat{a}\in \left[ a_{l},a_{u}\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] \) and \(\widehat{d}\in \left[ d_{l},d_{u}\right] .\) Also, \(a_{l}>0\), \(b_{l}>0\), \(c_{l}>0\), and \(d_{l}>0\).

4.2 Model with Parametric Interval Coefficient

The Eq. (2) can be written in the parametric form as follows

$$\begin{aligned} x_{n+1}= & {} (a_{l})^{1-p}(a_{u})^{p}x_{n}(1-x_{n})-(b_{l})^{1-p}(b_{u})^{p}\sqrt{x_{n}}y_{n} \\ y_{n+1}= & {} (c_{l})^{1-p}(c_{u})^{p}\sqrt{x_{n}}y_{n}-(d_{l})^{1-p}(d_{u})^{p}y_{n} \nonumber \end{aligned}$$
(3)

for \(p\in \left[ 0,1\right] \).

5 Fixed Points and Stability Analysis of Prey–Predator System

To find the fixed points of the system, we have to solve the following nonlinear system of equations:

\(x=(a_{l})^{1-p}(a_{u})^{p}x(1-x)-(b_{l})^{1-p}(b_{u})^{p}\sqrt{x}y\)

\(y=(c_{l})^{1-p}(c_{u})^{p}\sqrt{x}y-(d_{l})^{1-p}(d_{u})^{p}y\)

From the above nonlinear system of equations, we get these nonnegative fixed points as follows:

\(\left( i\right) \) \(P_{0}=\left( 0,0\right) ,\) \(\left( ii\right) \) \(P_{1}=\left( \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}},0\right) ,\) \((a_{l})^{1-p}(a_{u})^{p}>1,\) \(\left( iii\right) \) \( P_{2}=\left( x^{*},y^{*}\right) \) where \(x^{*}\) \(=\left( \frac{ (d_{l})^{1-p}(d_{u})^{p}+1}{(c_{l})^{1-p}(c_{u})^{p}}\right) ^{2}\)

and \(y^{*}=\frac{(a_{l})^{1-p}(a_{u})^{p}((d_{l})^{1-p}(d_{u})^{p}+1)}{(b_{l})^{1-p}(b_{u})^{p}(c_{l})^{1-p}(c_{u})^{p}}\left[ 1-\frac{1}{ (a_{l})^{1-p}(a_{u})^{p}}-\left( \frac{(d_{l})^{1-p}(d_{u})^{p}+1}{ (c_{l})^{1-p}(c_{u})^{p}}\right) ^{2}\right] , \left[ \frac{1}{ (a_{l})^{1-p}(a_{u})^{p}}+\left( \frac{(d_{l})^{1-p}(d_{u})^{p}+1}{ (c_{l})^{1-p}(c_{u})^{p}}\right) ^{2}\right] <1\)

5.1 Dynamic Behavior of the Model

This section presents the local behavior of the model (3) for each equilibrium points of the prey–predator system. The stability of the system (3) is carried out by computing the Jacobian matrix corresponding to each equilibrium point. The Jacobian matrix J for the system (3) is

\(J=\left[ \begin{array}{cc} (a_{l})^{1-p}(a_{u})^{p}(1-2x)-\frac{(b_{l})^{1-p}(b_{u})^{p}y}{2\sqrt{x}} &{} -(b_{l})^{1-p}(b_{u})^{p}\sqrt{x} \\ \frac{(c_{l})^{1-p}(c_{u})^{p}y}{2\sqrt{x}} &{} (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\end{array}\right] \)

Characteristic equation of matrix J is \(\lambda ^{2}-{\text {Tr}}\left( J\right) \lambda +{\text {Det}}\left( J\right) =0\) where

$$ \begin{aligned} {\text {Tr}}\left( J\right)&= \text {Trace of matrix}\ J \\&=\left[ (a_{l})^{1-p}(a_{u})^{p}(1-2x)-\frac{(b_{l})^{1-p}(b_{u})^{p}y}{2\sqrt{x}} \right] +\left[ (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p} \right] \end{aligned} $$
$$ \begin{aligned} {\text {Det}}(J)&= {\text {Determinant of matrix}} \ J \\&= (a_{l})^{1-p}(a_{u})^{p}(1-2x)\left( (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\right) \\&\quad +\frac{ (b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}} \end{aligned} $$

Hence, the model (3) is a dissipative dynamical system if

\(\left| (a_{l})^{1-p}(a_{u})^{p}(1-2x)\left( (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\right) +\frac{(b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}}\right| <1\)

conservative dynamical one, if and only if

\(\left| (a_{l})^{1-p}(a_{u})^{p}(1-2x)\left( (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\right) +\frac{(b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}}\right| =1\)

and is an un-dissipated dynamical system otherwise.

In order to study the stability of the fixed points of the model, we first give the following lemma

Lemma 1

Let \(F(\lambda )=\lambda ^{2}-B\lambda +C\). Suppose that \(F(1)>0,\) \(\lambda _{1}\) and \(\lambda _{2}\) are the two roots of \(F(\lambda )=0.\) Then

(i) \(|\lambda _{1}|<1\) and \(|\lambda _{2}|<1\) if and only if \(F(-1)>0\) and \(C<1;\)

(ii) \(|\lambda _{1}|<1\) and \(|\lambda _{2}|>1\) (or \(|\lambda _{1}|>1\) and \(|\lambda _{2}|<1)\) if and only if \(F(-1)<0;\)

(iii) \(|\lambda _{1}|>1\) and \(|\lambda _{2}|>1\) if and only if \(F(-1)>0\) and \(C>1;\)

(iv) \(\lambda _{1}=-1\) and \(|\lambda _{2}|\ne 1\) if and only if \(F(-1)=0\) and \(B\ne 0,2;\)

(v) \(\lambda _{1}\) and \(\lambda _{2}\) are complex and \(|\lambda _{1}|=|\lambda _{2}|=1\) if and only if \(B^{2}-4C<0\) and \(C=1.\)

Let \(\lambda _{1}\)and \(\lambda _{2}\) be the two eigenvalues of the fixed point (x, y). We recall some definitions of topological types for a fixed point (x, y).

A fixed point (x, y) is called

(i) a sink if \(|\lambda _{1}|<1\) and \(|\lambda _{2}|<1,\) so the sink is locally asymptotically stable.

(ii) a source if \(|\lambda _{1}|>1\) and \(|\lambda _{2}|>1,\) so the source is locally unstable.

(iii) a saddle if \(|\lambda _{1}|>1\) and \(|\lambda _{2}|<1\) or ( \(|\lambda _{1}|<1\) and \(|\lambda _{2}|>1\)).

(iv) non-hyperbolic if either \(|\lambda _{1}|=1\) or \(|\lambda _{2}|=1.\)

5.2 Stability and Dynamic Behavior of \(P_{1}\)

At \(P_{1}=\left( \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}},0\right) ,\) the Jacobian matrix J for the system is

\(J=\left[ \begin{array}{cc} 2-(a_{l})^{1-p}(a_{u})^{p} &{} -(b_{l})^{1-p}(b_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] } \\ 0 &{} (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\end{array}\right] \)

Equilibrium point is

Sink if \(\left| 2-(a_{l})^{1-p}(a_{u})^{p}\right| <1\) and \(\left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\right| <1\)

Source if \(\left| 2-(a_{l})^{1-p}(a_{u})^{p}\right| >1\) and \(\left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\right| >1\)

Saddle if \(\left| 2-(a_{l})^{1-p}(a_{u})^{p}\right| >1\) and \(\left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\right| <1\) or

\(\left| 2-(a_{l})^{1-p}(a_{u})^{p}\right| <1\) and \(\left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\right| >1\)

Non-hyperbolic if \(\left| 2-(a_{l})^{1-p}(a_{u})^{p}\right| =1\) or \( \left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] } -(d_{l})^{1-p}(d_{u})^{p}\right| =1\)

If \((a_{l})^{1-p}(a_{u})^{p}=3\) and \(\left| (c_{l})^{1-p}(c_{u})^{p}\sqrt{\left[ \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}}\right] }-(d_{l})^{1-p}(d_{u})^{p}\right| \ne 1\), then \(P_{1}=\left( \frac{(a_{l})^{1-p}(a_{u})^{p}-1}{(a_{l})^{1-p}(a_{u})^{p}},0\right) \) can undergo flip bifurcation when the parameters vary in the neighborhood of \((a_{l})^{1-p}(a_{u})^{p}=3.\)

5.3 Local Stability and Dynamic Behavior Around Interior Fixed Point

The dynamic behavior for the interior equilibrium point of the system is presented here:

$$ \begin{aligned}&1-{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) \\&=1-\left[ (a_{l})^{1-p}(a_{u})^{p}(1-2x)-\frac{(b_{l})^{1-p}(b_{u})^{p}y}{2\sqrt{x}}\right] \\&\quad -\left[ (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p} \right] \ \\&\quad +(a_{l})^{1-p}(a_{u})^{p}(1-2x)\left( (c_{l})^{1-p}(c_{u})^{p} \sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\right) \\&\quad +\frac{ (b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}} \end{aligned} $$
$$ \begin{aligned}&1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) \\&= 1+\left[ (a_{l})^{1-p}(a_{u})^{p}(1-2x)-\frac{(b_{l})^{1-p}(b_{u})^{p}y}{2\sqrt{x}} \right] \\&\quad +\left[ (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}-(d_{l})^{1-p}(d_{u})^{p} \right] \ +(a_{l})^{1-p}(a_{u})^{p}(1-2x)\\&\; \left( (c_{l})^{1-p}(c_{u})^{p} \sqrt{x}-(d_{l})^{1-p}(d_{u})^{p}\right) +\frac{ (b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}} \end{aligned} $$
$$ \begin{aligned} {\text {Det}}\left( J\right)&=(a_{l})^{1-p}(a_{u})^{p}(1-2x)\left( (c_{l})^{1-p}(c_{u})^{p}\sqrt{x}\right. \\&\left. \quad -(d_{l})^{1-p}(d_{u})^{p}\right) +\frac{ (b_{l})^{1-p}(b_{u})^{p}(d_{l})^{1-p}(d_{u})^{p}y}{2\sqrt{x}} \end{aligned} $$

At \(P_{2}=\left( x^{*},y^{*}\right) , \) if \(1-{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0\), then interior equilibrium point is

Sink if \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0\) and \({\text {Det}}\left( J\right) <1\)

Source if \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0\) and \({\text {Det}}\left( J\right) >1\)

Saddle if \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) <0\)

Non-hyperbolic if \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) =0\) and \({\text {Tr}}\left( J\right) \ne 0,2.\) or \(\left[ {\text {Tr}}\left( J\right) \right] ^{2}-4{\text {Det}}\left( J\right) <0\) and \({\text {Det}}\left( J\right) =1.\)

At \(P_{2}=\left( x^{*},y^{*}\right) , \) if \(1-{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0\), \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) =0\), and \({\text {Tr}}\left( J\right) \ne 0 and 2\), then \(\left( x^{*},y^{*}\right) \) can undergo flip bifurcation.

At \(P_{2}=\left( x^{*},y^{*}\right) , \) if \(1-{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0\), \(\left( {\text {Tr}}\left( J\right) \right) ^{2}-4{\text {Det}}\left( J\right) <0\) and \({\text {Det}}\left( J\right) =1\), then \(\left( x^{*},y^{*}\right) \) can undergo Hopf bifurcation.

6 Flip Bifurcation

From Lemma 1, one of the eigenvalues of the positive fixed point \(P_{2}=\left( x^{*},y^{*}\right) \) is \(\lambda _{1}=\) \(-1\) and the other \(\left( \lambda _{2}\right) \) is neither 1 nor \(-1\) if parameters of the model are located in the following set \(A=\{\left( a_{l},a_{u},b_{l},b_{u},c_{l},c_{u},d_{l},d_{u},p\right) \): \(1-{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) >0,\) \(1+{\text {Tr}}\left( J\right) +{\text {Det}}\left( J\right) =0,\) \({\text {Tr}}\left( J\right) \ne 0,2\) and \(p\in \left[ 0,1\right] \}.\)

Here, we discuss flip bifurcation of the model (3) at \(P_{2}=\left( x^{*},y^{*}\right) \) when parameters vary in a small neighborhood of A. In analyzing the flip bifurcation, p is used as the bifurcation parameter. Further, \(p^{*}\) is the perturbation of p,  we consider a perturbation of the system as follows:

$$\begin{aligned} x_{n+1}&=(a_{l})^{1-(p+p^{*})}(a_{u})^{(p+p^{*})}x_{n}(1-x_{n})-(b_{l})^{1-(p+p^{*})}(b_{u})^{(p+p^{*})}\sqrt{x_{n}}y_{n}\equiv f(x_{n},y_{n},p^{*}) \\ y_{n+1}&=(c_{l})^{1-(p+p^{*})}(c_{u})^{(p+p^{*})}\sqrt{x_{n}}y_{n}-(d_{l})^{1-(p+p^{*})}(d_{u})^{(p+p^{*})}y_{n}\equiv g(x_{n},y_{n},p^{*}) \nonumber \end{aligned}$$
(4)

where \(\left| p^{*}\right| \lll 1\)

Let \(u_{n}=x_{n}-x^{*},v_{n}=y_{n}-y^{*},\) then equilibrium \(P_{2}=\left( x^{*},y^{*}\right) \) is transformed into the origin, and further expanding f and g as a Taylor series at \((u_{n},v_{n},p^{*})=(0,0,0)\) to the third order, the model (4) becomes

$$\begin{aligned} u_{n+1}= & {} \alpha _{1}u_{n}+\alpha _{2}v_{n}+\alpha _{11}u_{n}^{2}+\alpha _{12}u_{n}v_{n}+\alpha _{13}u_{n}p^{*}+\alpha _{23}v_{n}p^{*}+ \\&\alpha _{111}u_{n}^{3}+\alpha _{112}u_{n}^{2}v_{n}+\alpha _{113}u_{n}^{2}p^{*}+\alpha _{123}u_{n}v_{n}p^{*}+O((\left| u_{n}\right| +\left| v_{n}\right| +\left| p^{*}\right| )^{4}) \nonumber \\ v_{n+1}= & {} \beta _{1}u_{n}+\beta _{2}v_{n}+\beta _{11}u_{n}^{2}+\beta _{12}u_{n}v_{n}+\beta _{22}v_{n}^{2}+\beta _{13}u_{n}p^{*}+\beta _{23}v_{n}p^{*}+\beta _{111}u_{n}^{3}+ \nonumber \\&\beta _{112}u_{n}^{2}v_{n}+\beta _{113}u_{n}^{2}p^{*}+\beta _{123}u_{n}v_{n}p^{*}+\beta _{223}v_{n}^{2}p^{*}+O((\left| u_{n}\right| +\left| v_{n}\right| +\left| p^{*}\right| )^{4}) \nonumber \end{aligned}$$
(5)

where \(\alpha _{1}=f_{x}(x^{*},y^{*},0),\) \(\alpha _{2}=f_{y}(x^{*},y^{*},0),\) \(\alpha _{11}=f_{xx}(x^{*},y^{*},0),\) \(\alpha _{12}=f_{xy}(x^{*},y^{*},0),\) \(\alpha _{13}=f_{xp^{*}}(x^{*},y^{*},0),\) \(\alpha _{23}=f_{yp^{*}}(x^{*},y^{*},0),\) \(\alpha _{111}=f_{xxx}(x^{*},y^{*},0),\) \(\alpha _{112}=f_{xxy}(x^{*},y^{*},0),\) \(\alpha _{113}=f_{xxp^{*}}(x^{*},y^{*},0),\) \(\alpha _{123}=f_{xyp^{*}}(x^{*},y^{*},0)\)

\(\beta _{1}=g_{x}(x^{*},y^{*},0),\beta _{2}=g_{y}(x^{*},y^{*},0),\beta _{11}=g_{xx}(x^{*},y^{*},0),\) \(\beta _{12}=g_{xy}(x^{*},y^{*},0),\) \(\beta _{22}=g_{yy}(x^{*},y^{*},0),\) \(\beta _{13}=g_{xp^{*}}(x^{*},y^{*},0),\) \(\beta _{23}=g_{yp^{*}}(x^{*},y^{*},0),\) \(\beta _{111}=g_{xxx}(x^{*},y^{*},0),\) \(\beta _{112}=g_{xxy}(x^{*},y^{*},0),\) \(\beta _{113}=g_{xxp^{*}}(x^{*},y^{*},0),\) \(\beta _{123}=g_{xyp^{*}}(x^{*},y^{*},0),\) \(\beta _{223}=g_{yyp^{*}}(x^{*},y^{*},0)\)

We define \(T=\left[ \begin{array}{cc} \alpha _{2} &{} \alpha _{2} \\ -1-\alpha _{1} &{} \lambda _{2}-\alpha _{1}\end{array}\right] ,\) where T is invertible, and using the transformation \(\left[ \begin{array}{c} u_{n} \\ v_{n}\end{array}\right] =T\left[ \begin{array}{c} \overline{x}_{n} \\ \overline{y}_{n}\end{array}\right] \), the model (5) becomes

$$\begin{aligned} \overline{x}_{n+1}= & {} -\overline{x}_{n}+f_{1}(u_{n},v_{n},p^{*}) \\ \overline{y}_{n+1}= & {} \lambda _{2}\overline{y}_{n}+g_{1}(u_{n},v_{n},p^{*}) \nonumber \end{aligned}$$
(6)

where the functions \(f_{1}\) and \(g_{1}\) denote the terms in the model (6) in variables \((u_{n},v_{n},p^{*})\) with the order at least two.

From the theorem of center manifold, there exists a center manifold \(W^{c}(0,0,0)\) of the model (6) at (0, 0) in a small neighborhood of \(p^{*}=0,\) which can be approximately described as follows:

\(W^{c}(0,0,0)=\left\{ \left( \overline{x}_{n},\overline{y}_{n},p^{*}\right) \epsilon R^{3}:\overline{y}_{n+1}=\overline{\alpha }_{1}\overline{x}_{n}^{2} +\overline{\alpha }_{2}\overline{x}_{n}p^{*}+O((\left| \overline{x}_{n}\right| +\left| p^{*}\right| )^{3})\right\} \)

where \(\overline{\alpha }_{1}=\dfrac{\alpha _{2}[(1+\alpha _{1})\alpha _{11}+\alpha _{2}\beta _{11}]}{1-\lambda _{2}^{2}}+\dfrac{\beta _{22}(1+\alpha _{1})^{2}}{1-\lambda _{2}^{2}}-\dfrac{(1+\alpha _{1})[\alpha _{12}(1+\alpha _{1})+\alpha _{2}\beta _{12}]}{1-\lambda _{2}^{2}}\), \( \overline{\alpha }_{2}=\dfrac{(1+\alpha _{1})[\alpha _{23}(1+\alpha _{1})+\alpha _{2}\beta _{23}]}{\alpha _{2}(1+\lambda _{2})^{2}}-\dfrac{ (1+\alpha _{1})\alpha _{13}+\alpha _{2}\beta _{13}]}{(1+\lambda _{2})^{2}}.\)

We obtain the system (6) restricted to center manifold \(W^{c}(0,0,0),\) which has the following form

\(\overline{x}_{n+1}=-\overline{x}_{n}+h_{1}\overline{x}_{n}^{2}+h_{2}\overline{x}_{n}p^{*}+h_{3}\overline{x}_{n}^{2}p^{*}+h_{4}\overline{x}_{n}p^{*2}+h_{5}\overline{x}_{n}^{3}+O((\left| \overline{x}_{n}\right| +\left| p^{*}\right| )^{3})\equiv F(\overline{x}_{n},p^{*})\)

$$\begin{aligned} h_{1}&=\frac{\overline{\alpha }_{2}[(\lambda _{2}-\overline{\alpha } _{1})\alpha _{11}-\overline{\alpha }_{2}\beta _{11}]}{1+\lambda _{2}}-\frac{ \beta _{22}(1+\overline{\alpha }_{1})^{2}}{1+\lambda _{2}}-\frac{(1+ \overline{\alpha }_{1})[(\lambda _{2}-\overline{\alpha }_{1})\alpha _{12}- \overline{\alpha }_{2}\beta _{12}]}{1+\lambda _{2}},\\ h_{2}&=\frac{(\lambda _{2}-\overline{\alpha }_{1})\alpha _{13}-\overline{ \alpha }_{2}\beta _{13}}{1+\lambda _{2}}-\frac{(1+\overline{\alpha } _{1})[(\lambda _{2}-\overline{\alpha }_{1})\alpha _{23}-\overline{\alpha } _{2}\beta _{23}]}{\overline{\alpha }_{2}\left( 1+\lambda _{2}\right) },\\ h_{3}&=\frac{(\lambda _{2}-\alpha _{1})\overline{\alpha }_{1}\alpha _{13}-\alpha _{2}\beta _{13}}{1+\lambda _{2}}+\frac{[(\lambda _{2}-\alpha _{1})\alpha _{23}-\alpha _{2}\beta _{23}](\lambda _{2}-\alpha _{1})\overline{ \alpha }_{1}}{\alpha _{2}\left( 1+\lambda _{2}\right) }\\&-\frac{(1+\alpha _{1})[(\lambda _{2}-\alpha _{1})\alpha _{123}-\alpha _{2}\beta _{123}]}{ 1+\lambda _{2}}+\frac{\alpha _{2}[(\lambda _{2}-\alpha _{1})\alpha _{113}-\alpha _{2}\beta _{113}]}{1+\lambda _{2}} \\&- \frac{\beta _{223}(1+\alpha _{1})^{2}}{1+\lambda _{2}} +\frac{2\alpha _{2}\overline{\alpha }_{2}[(\lambda _{2}-\alpha _{1})\alpha _{11}-\alpha _{2}\beta _{11}]}{1+\lambda _{2}}-\frac{2\beta _{22} \overline{\alpha }_{2}(1+\alpha _{1})(\lambda _{2}-\alpha _{1})}{1+\lambda _{2}}\\&+\frac{\overline{\alpha }_{2}[(\lambda _{2}-\alpha _{1})\alpha _{12}-\alpha _{2}\beta _{12}](\lambda _{2}-1-2\alpha _{1})}{1+\lambda _{2}},\\ h_{4}&=\frac{\overline{\alpha }_{2}[(\lambda _{2}-\alpha _{1})\alpha _{13}-\alpha _{2}\beta _{13}]}{1+\lambda _{2}}+\frac{[(\lambda _{2}-\alpha _{1})\alpha _{23}-\alpha _{2}\beta _{23}](\lambda _{2}-\alpha _{1})\overline{ \alpha }_{2}}{\alpha _{2}\left( 1+\lambda _{2}\right) }\\&+\frac{2\alpha _{2} \overline{\alpha }_{2}[(\lambda _{2}-\alpha _{1})\alpha _{11}-\alpha _{2}\beta _{11}]}{1+\lambda _{2}} \\&+ \frac{2\beta _{22}\overline{\alpha }_{2}(1+\alpha _{1})(\lambda _{2}-\alpha _{1})}{1+\lambda _{2}} +\frac{\overline{\alpha }_{2}[(\lambda _{2}-\alpha _{1})\alpha _{12}-\alpha _{2}\beta _{12}](\lambda _{2}-1-2\alpha _{1})}{1+\lambda _{2}},\\ h_{5}&=\frac{2\alpha _{2}\overline{\alpha }_{1}[(\lambda _{2}-\alpha _{1})\alpha _{11}-\alpha _{2}\beta _{11}]}{1+\lambda _{2}}+\frac{2\beta _{22} \overline{\alpha }_{1}(\lambda _{2}-\alpha _{1})(1+\alpha _{1})}{1+\lambda _{2}}\\&+\frac{[(\lambda _{2}-\alpha _{1})\alpha _{11}-\alpha _{2}\beta _{11}](\lambda _{2}-1-2\alpha _{1})\overline{\alpha }_{1}}{1+\lambda _{2}}\\&+\frac{\overline{\alpha }_{2}^{2}[(\lambda _{2}-\alpha _{1})\alpha _{111}-\alpha _{2}\beta _{111}]}{1+\lambda _{2}}-\frac{ \overline{\alpha }_{2}(1+\alpha _{1})[(\lambda _{2}-\alpha _{1})\alpha _{112}-\alpha _{2}\beta _{112}]}{1+\lambda _{2}}. \end{aligned}$$

For flip bifurcation, we require the two discriminatory quantities \(\xi _{1}\) and \(\xi _{2}\) to be nonzero,

\(\xi _{1}=\left( \frac{\partial ^{2}F}{\partial \overline{x}\partial p^{*}}+\frac{1}{2}\frac{\partial F}{\partial p^{*}}\frac{\partial ^{2}F}{\partial \overline{x}^{2}}\right) \mid _{(0,0)}\)

\(\xi _{2}=\left( \frac{1}{6}\frac{\partial ^{3}F}{\partial \overline{x}^{3}}+\left( \frac{1}{2}\frac{\partial ^{2}F}{\partial \overline{x}^{2}}\right) ^{2}\right) \mid _{(0,0)}\)

Finally, from the above analysis , we have the following result.

Theorem 2

If \(\xi _{1}\ne 0\) and \(\xi _{2}\ne 0\) then the model (3) undergoes flip bifurcation at \(P_{2}=\left( x^{*},y^{*}\right) \), if \(\xi _{2}>0\) (resp. \(\xi _{2}<0),\) then the period-2 points that bifurcation from \(P_{2}=\left( x^{*},y^{*}\right) \) are stable.

7 Chaos Control

This section presents a feedback control method to stabilize chaotic orbits at an unstable positive fixed point of system (3).

Consider the following controlled form of model (3):

$$\begin{aligned} x_{n+1}= & {} (a_{l})^{1-p}(a_{u})^{p}x_{n}(1-x_{n})-(b_{l})^{1-p}(b_{u})^{p}\sqrt{x_{n}}y_{n}+S \\ y_{n+1}= & {} (c_{l})^{1-p}(c_{u})^{p}\sqrt{x_{n}}y_{n}-(d_{l})^{1-p}(d_{u})^{p}y_{n} \nonumber \end{aligned}$$
(7)

with the following feedback control law as the control force:

$$ S=-q_{1}\left( x_{n}-x^{*}\right) -q_{2}\left( y_{n}-y^{*}\right) $$

where \(q_{1}\) and \(q_{2}\) are the feedback gain and \(\left( x^{*},y^{*}\right) \) is a positive fixed point of model.

The Jacobian matrix J for the system (7) at \(\left( x^{*},y^{*}\right) \) is

\(J=\left[ \begin{array}{cc} a_{11}-q_{1} &{} a_{12}-q_{2} \\ a_{21} &{} a_{22}\end{array}\right] \)

where \(a_{11}\,{=}\,a_{l}{}^{1-p}a_{u}{}^{p}(1-2x^{*})\,{-}\,\frac{b_{l}{}^{1-p}b_{u}{}^{p}y^{*}}{2\sqrt{x^{*}}},a_{12}=-b_{l}{}^{1-p}b_{u}{}^{p}\sqrt{x^{*}},a_{21}\,{=}\,\frac{c_{l}{}^{1-p}c_{u}{}^{p}y^{*}}{2\sqrt{x^{*}}},a_{22}=c_{l}{}^{1-p}c_{u}{}^{p}\sqrt{x^{*}}-d_{l}{}^{1-p}d_{u}{}^{p}.\) The corresponding characteristic equation of matrix J is

\(\lambda ^{2}-\left( a_{11}+a_{22}-q_{1}\right) \lambda +a_{22}\left( a_{11}-q_{1}\right) -a_{21}\left( a_{12}-q_{2}\right) \)

Let \(\lambda _{1}\) and \(\lambda _{2}\) are the eigenvalues

$$\begin{aligned} \lambda _{1}+\lambda _{2}=a_{11}+a_{22}-q_{1} \end{aligned}$$
(8)

and

$$\begin{aligned} \lambda _{1}\lambda _{2}=a_{22}\left( a_{11}-q_{1}\right) -a_{21}\left( a_{12}-q_{2}\right) \end{aligned}$$
(9)

The lines of marginal stability are determined by solving the equation \(\lambda _{1}=\pm 1\) and \(\lambda _{1}\lambda _{2}=1.\) These conditions guarantee that the eigenvalues \(\lambda _{1}\) and \(\lambda _{2}\) have modulus less than 1.

Suppose \(\lambda _{1}\lambda _{2}=1\); from (9)  we have line \(l_{1}\) as follows:

\(a_{22}q_{1}-a_{21}q_{2}=a_{22}a_{11}-a_{21}a_{12}-1\)

Suppose \(\lambda _{1}=\pm 1;\) from (8, 9), we have line \(l_{2}\) and \(l_{3}\) as follows:

\(\left( 1-a_{22}\right) q_{1}+a_{21}q_{2}=a_{11}+a_{22}-1-a_{22}a_{11}+a_{21}a_{12}\)

and

\(\left( 1+a_{22}\right) q_{1}-a_{21}q_{2}=a_{11}+a_{22}+1+a_{22}a_{11}-a_{21}a_{12}\)

The stable eigenvalues lie within a triangular region by line \(l_{1},l_{2}\) and \(l_{3}\).

8 Numerical Simulation

Here, we consider a numerical example of the above model and carried out mathematical calculation that depends on some artificial data. We calculated the equilibrium points and analyzed their stability. For the model (3) given in the paper, we consider the parameter values \(\widehat{a}\in \left[ a_{l},a_{u}\right] =\left[ 4.0,4.2\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] =\left[ 1.8,2.0\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] =\left[ 1.7,1.9\right] \), \(\widehat{d}\in \left[ d_{l},d_{u}\right] =\left[ 0.1,0.2\right] .\) Performing computer simulation on that chosen data, we calculate the equilibria points, eigenvalues and stability of every equilibrium points for different values of p. The obtained results are given in Table 1.

Table 1 Equilibrium points, Eigenvalues and stability of equilibrium points
Full size table
Fig. 1
figure 1

Time graph for different p

Full size image
Fig. 2
figure 2

Phase portrate for different p

Full size image

Figures 1 and 2 are drawn in the basis of the parameter values \(\widehat{a}\in \left[ a_{l},a_{u}\right] =\left[ 4.0,4.2\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] =\left[ 1.8,2.0\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] =\left[ 1.7,1.9\right] \), \(\widehat{d}\in \left[ d_{l},d_{u}\right] =\left[ 0.1,0.2\right] .\) Here, we observe damped oscillation for time plot in Fig. 1 for \(p=0.0,0.2,0.4,0.6,0.8\). In Fig. 2, all trajectories spiral into the stable fixed point for \(p=0.0,0.2,0.4,0.6,0.8\). Here, we found constant oscillation about interior equilibrium points for time plot in Fig. 1 for \(p=1.0\) . In Fig. 2, trajectories are attracted to a limit cycle about interior equilibrium points for \(p=1.0\). Hence, there exist a bifurcation for p. This bifurcation is supercritical—after the fixed point loses stability, it is surrounded by a stable limit cycle.

Fig. 3
figure 3

Bifurcation diagram for varying p

Full size image
Fig. 4
figure 4

Bifurcation diagram for varying p

Full size image

Figure 3 depicts smooth invariant circle bifurcates for both prey and predator from stable equilibrium. As the p value increases, the behavior becomes more complex and more unpredictable for both species. When p exceeds 0.91, there appears a circular curve enclosing equilibrium and its radius becomes larger with chaotic behavior for both species. This figure is drawn with respect to \(\widehat{a}\in \left[ a_{l},a_{u}\right] =\left[ 4.0,4.2\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] =\left[ 1.8,2.0\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] =\left[ 1.7,1.9\right] \), \(\widehat{d}\in \left[ d_{l},d_{u}\right] =\left[ 0.1,0.2\right] . \)

Fig. 5
figure 5

Bifurcation diagram for varing p

Full size image

Figure 4 shows a smooth invariant circle bifurcates from stable equilibrium. When p exceeds 0.7, there appears a circular curve enclosing equilibrium and its radius becomes larger with the increasing of p.This figure is drawn with respect to \(\widehat{a}\in \left[ a_{l},a_{u}\right] =\left[ 4.2,4.4\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] =\left[ 1.8,2.0\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] =\left[ 1.7,1.9\right] \), \(\widehat{d}\in \left[ d_{l},d_{u}\right] =\left[ 0.1,0.2\right] . \)

The above figure is drawn with respect to \(\widehat{a}\in \left[ a_{l},a_{u}\right] =\left[ 4.5,4.7\right] \), \(\widehat{b}\in \left[ b_{l},b_{u}\right] =\left[ 1.8,2.0\right] \), \(\widehat{c}\in \left[ c_{l},c_{u}\right] =\left[ 1.7,1.9\right] \), \(\widehat{d}\in \left[ d_{l},d_{u}\right] =\left[ 0.1,0.2\right] .\) Figure 5 shows smooth invariant circle bifurcates for both species from stable equilibrium. Furthermore, if p exceeds 0.45, there appears a circular curve enclosing equilibrium and its radius becomes larger with the growth of p. At p values above 0.83, the systems behave as a limit cycle for both species.

9 Conclusion

This work is related to the qualitative behavior of a discrete-time predator-prey model under imprecise biological parameters. We have found the fixed points of the system and discussed their stability analytically. We give a flip bifurcation analysis and chaos control procedure. The phase portraits, bifurcation and time graphs are obtained for different parameters of the model. Here, we introduce a new concept in bifurcation analysis. The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. When we consider p as bifurcation parameter, ultimately, we consider here 4 bifurcation parameter in a certain range, but interesting fact is that using our technic we convert this 4 codim bifurcation in 1 codim. The proposed study will be very useful for the mathematical modeling and analysis of a wide range of predator–prey interactions. Our study suggests that herd behavior has stabilizing effect on population dynamics.