Component Elimination Strategies to Fit Mixtures of Multiple Scale Distributions

Abstract

We address the issue of selecting automatically the number of components in mixture models with non-Gaussian components. As a more efficient alternative to the traditional comparison of several model scores in a range, we consider procedures based on a single run of the inference scheme. Starting from an overfitting mixture in a Bayesian setting, we investigate two strategies to eliminate superfluous components. We implement these strategies for mixtures of multiple scale distributions which exhibit a variety of shapes not necessarily elliptical while remaining analytical and tractable in multiple dimensions. A Bayesian formulation and a tractable inference procedure based on variational approximation are proposed. Preliminary results on simulated and real data show promising performance in terms of model selection and computational time.

1 Introduction

A difficult problem when fitting mixture models is to determine the number K of components to include in the mixture. A recent review on the problem with theoretical and practical aspects can be found in [10]. Traditionally, this selection is performed by comparing a set of candidate models for a range of values of K, assuming that the true value is in this range. The number of components is selected by minimizing a model selection criterion, such as the Bayesian inference criterion (BIC), minimum message length (MML), Akaike’s information criteria (AIC) to cite just a few [13, 23]. Of a slightly different nature is the so-called slope heuristic [7], which involves a robust linear fit and is not simply based on criterion comparisons. However, the disadvantage of these approaches is that a whole set of candidate models has to be obtained and problems associated with running inference algorithms (such as EM) many times may emerge. When the components distributions complexity increases, it may then be desirable to avoid repetitive inference of models that will be discarded in the end. For standard Gaussian distributions however, this is not really a problem as efficient software such as Mclust [28] are available. Alternatives have been investigated that select the number of components from a single run of the inference scheme. Apart from the Reversible Jump Markov Chain Monte Carlo method of [26] which allows jumps between different numbers of components, two types of approaches can be distinguished depending on whether the strategy is to increase or to decrease the number of components. The first ones can be referred to as greedy algorithms (e.g. [30]) where the mixture is built component-wise, starting with the optimal one-component mixture and increasing the number of components until a stopping criterion is met. More recently, there seems to be an increase interest among mixture model practitioners for model selection strategies that start instead with a large number of components and merge them [18]. For instance, [13] proposes a practical algorithm that starts with a very large number of components, iteratively annihilates components, redistributes the observations to the other components, and terminates based on the MML criterion. The approach in [6] starts with an overestimated number of components using BIC, and then merges them hierarchically according to an entropy criterion, while [24] proposes a similar method that merges components based on measuring their pair-wise overlap. Another trend in handling the issue of finding the proper number of components is to consider Bayesian non-parametric mixture models. This allows the implementation of mixture models with an infinite number of components via the use of Dirichlet process mixture models. In [17, 25] an infinite Gaussian mixture (IGMM) is presented with a computationally intensive Markov Chain Monte Carlo implementation. More recently, more flexibility in the cluster shapes has been allowed by considering infinite mixture of infinite Gaussian mixtures (I$^2$GMM) [32]. The flexibility is however limited to a cluster composed of sub-clusters of identical shapes and orientations, which may alter the performance of this approach. Beyond the Gaussian case, infinite Student mixture models have also been considered [31]. The Bayesian non-parametric approach is a promising technique. In this work, we consider a Bayesian formulation but in the simpler case of a finite number of components. We suspect all our Bayesian derivations could be easily tested in a non parametric setting with some minor adaptation left for future work. Following common practice that is to start from deliberately overfitting mixtures (e.g. [3, 11, 21, 22]), we investigate component elimination strategies. Component elimination refers to a natural approach which is to exploit the vanishing component phenomenon that has been proved to occur in certain Bayesian settings [27]. This requires a Bayesian formulation of the mixture for the regularization effect due to the integration of parameters in the posterior distribution. This results in an implicit penalization for model complexity. Although this approach can be based on arbitrary mixture components, most previous investigation has been confined to Gaussian mixtures where the mixture components arise from multivariate Gaussian densities with component-specific parameters.

In this work, we address the issue of selecting automatically the number of components in a non-Gaussian case. We consider mixtures of so called multiple scale distributions for their ability to handle a variety of shapes not necessarily elliptical while remaining analytical and tractable. We propose a Bayesian formulation of these mixtures and a tractable inference procedure based on a variational approximation. We propose two different single-run strategies that make use of the component elimination property.

The rest of the paper is organized as follows. Mixture of multiple scale distributions, their Bayesian formulation and inference are specified in Sect. 2. The two proposed strategies are described in Sect. 3, illustrated with experiments on simulated data in Sect. 4.

2 Bayesian Mixtures of Multiple Scale Distributions

2.1 Multiple Scale Mixtures of Gaussians

A M-variate scale mixture of Gaussians is a distribution of the form:

$$\begin{aligned} p(\mathbf {y};{\varvec{\mu }}, {\varvec{\varSigma }},{\varvec{\theta }}) = \displaystyle {\int _{0}^{\infty }} \mathcal {N}_M(\mathbf {y};{\varvec{\mu }},{\varvec{\varSigma }}/w)\; f_W(w;{\varvec{\theta }}) \; \text {d}w \end{aligned}$$

(1)

where $\mathcal {N}_M(\; . \; ;{\varvec{\mu }},{\varvec{\varSigma }}/w)$ denotes the M-dimensional Gaussian distribution with mean ${\varvec{\mu }}$, covariance ${\varvec{\varSigma }}/w$ and $f_W$ is the probability distribution of a univariate positive variable W referred to hereafter as the weight variable. A common form is obtained when $f_W$ is a Gamma distribution $\mathcal{G}(\nu /2, \nu /2)$ where $\nu$ denotes the degrees of freedom (we shall denote the Gamma distribution when the variable is X by $\mathcal{G}(x;\alpha , \gamma ) = x^{\alpha -1} \varGamma (\alpha )^{-1} \exp (-\gamma x) \gamma ^\alpha$ where $\varGamma$ denotes the Gamma function). For this form, (1) is the density denoted by $t_M(\mathbf {y};{\varvec{\mu }}, {\varvec{\varSigma }},\nu )$ of the M-dimensional Student t-distribution with parameters ${\varvec{\mu }}$ (real location vector), ${\varvec{\varSigma }}$ ($M\times M$ real positive definite scale matrix) and $\nu$ (positive real degrees of freedom parameter).

The extension proposed by [14] consists of introducing a multidimensional weight. To do so, the scale matrix is decomposed into eigenvectors and eigenvalues. This spectral decomposition is classically used in Gaussian model-based clustering [5, 9]. In a Bayesian setting, it is equivalent but more convenient to use matrix ${\varvec{T}}$ the inverse of the scale matrix. We therefore consider the decomposition ${\varvec{T}} = {\varvec{D}} {\varvec{A}} {\varvec{D}} ^T$ where ${\varvec{D}}$ is the matrix of eigenvectors of ${\varvec{T}}$ (equivalently of ${\varvec{\varSigma }}$) and ${\varvec{A}}$ is a diagonal matrix with the corresponding eigenvalues. The matrix ${\varvec{D}}$ determines the orientation of the Gaussian and ${\varvec{A}}$ its shape. Using this parameterization of ${\varvec{T}}$, the scale Gaussian part in (1) is set to $\mathcal{N}_M(\mathbf {y}; {\varvec{\mu }}, {\varvec{D}} {\varvec{\varDelta }} _{\mathbf {w}} {\varvec{A}} ^{-1} {\varvec{D}} ^T )$, where ${\varvec{\varDelta }} _\mathbf {w}=\text {diag}(w_{1}^{-1}, \ldots , w_{M}^{-1})$ is the $M \times M$ diagonal matrix whose diagonal components are the inverse weights $\{w_{1}^{-1}, \ldots , w_{M}^{-1}\}$. The multiple scale generalization consists therefore of:

$$\begin{aligned} p(\mathbf {y}; {\varvec{\mu }}, {\varvec{\varSigma }}, {\varvec{\theta }}) = {\int _{0}^{\infty }}... {\int _{0}^{\infty }} \mathcal {N}_M(\mathbf {y};{\varvec{\mu }},\; {\varvec{D}} {\varvec{\varDelta }} _\mathbf {w}{\varvec{A}} ^{-1} {\varvec{D}} ^T) \; f_\mathbf {w}(w_1... w_M ; {\varvec{\theta }}) \; \text {d}w_1 ... \text {d}w_M \; \end{aligned}$$

(2)

where $f_\mathbf {w}$ is now a M-variate density depending on some parameter ${\varvec{\theta }}$ to be further specified. In what follows, we will consider only independent weights, i.e. ${\varvec{\theta }} =\{{\varvec{\theta }} _1, \ldots , {\varvec{\theta }} _M\}$ with $f_\mathbf {w}(w_1\ldots w_M; {\varvec{\theta }}) = f_{W_1}(w_1 ; {\varvec{\theta }} _1) \ldots f_{W_M}(w_M; {\varvec{\theta }} _M).$ For instance, setting $f_{W_m}(w_m ; \theta _m)$ to a Gamma distribution $\mathcal{G}(w_m ; \alpha _m, \gamma _m)$ results in a multivariate generalization of a Pearson type VII distribution (see e.g. [20] vol. 2 chap. 28 for a definition of the Pearson type VII distribution). For identifiability, this model needs to be further specified by fixing all $\gamma _m$ parameters, for instance to 1. Despite this additional constraint, the decomposition of ${\varvec{\varSigma }}$ still induces another identifiability issue due to invariance to a same permutation of the columns of ${\varvec{D}}, {\varvec{A}}$ and elements of ${\varvec{\alpha }} =\{\alpha _1, \ldots , \alpha _M\}$. In a frequentist setting this can be solved by imposing a decreasing order for the eigenvalues in ${\varvec{A}}$. In a Bayesian setting one way to solve the problem is to impose on ${\varvec{A}}$ a non symmetric prior (see Sect. 2.2). An appropriate prior on ${\varvec{D}}$ would be more difficult to set. The distributions we consider are therefore of the form,

$$\begin{aligned} \mathcal{MP}(\mathbf {y}; {\varvec{\mu }}, {\varvec{D}}, {\varvec{A}}, {\varvec{\alpha }}) = \prod _{m=1}^M \frac{\varGamma (\alpha _{m}+1/2) A_m}{\varGamma (\alpha _{m}) (2 \pi )^{1/2}} \bigg (1+ \frac{ A_m [{\varvec{D}} ^T(\mathbf {y}-{\varvec{\mu }})]^2_{m}}{2 }\bigg )^{-(\alpha _{m} + 1/2)} \end{aligned}$$

(3)

Let us consider an i.i.d sample $\mathbf {y}=\{\mathbf {y}_1, \ldots , \mathbf {y}_N\}$ from a K-component mixture of multiple scale distributions as defined in (3). With the usual notation for the mixing proportions ${\varvec{\pi }} =\{\pi _1, \ldots , \pi _K\}$ and ${\varvec{\psi }} _k =\{{\varvec{\mu }} _k, {\varvec{A}} _k, {\varvec{D}} _k, {\varvec{\alpha }} _k\}$ for $k=1 \ldots K$, we consider,

$$ p(\mathbf {y};{\varvec{\varPhi }}) = \sum _{k=1}^{K}\pi _k \mathcal{MP} (\mathbf {y};{\varvec{\mu }} _k,{\varvec{A}} _k, {\varvec{D}} _k, {\varvec{\alpha }} _{k})$$

where ${\varvec{\varPhi }} =\{{\varvec{\pi }}, {\varvec{\psi }} \}$ with ${\varvec{\psi }} =\{{\varvec{\psi }} _1, \ldots {\varvec{\psi }} _K\}$ denotes the mixture parameters. Additional variables can be introduced to identify the class labels: $\{Z_1,\dots ,Z_N\}$ define respectively the components of origin of $\{\mathbf {y}_1,\dots ,\mathbf {y}_N\}$. An equivalent modelling is therefore:

$$\forall i \in \{1\ldots N\}, \quad \mathbf {Y}_i | \mathbf {W}_{i}= \mathbf {w}_i, Z_i= k, {\varvec{\psi }} \sim \mathcal{N}({\varvec{\mu }} _k, {\varvec{D}} _k {\varvec{\varDelta }} _{\mathbf {w}_i} {\varvec{A}} _k^{-1} {\varvec{D}} _k^T)\; ,$$

$$ \qquad \mathbf {W}_{i} | Z_i=k, {\varvec{\psi }} \sim \mathcal{G}(\alpha _{k1}, 1) \otimes \ldots \otimes \mathcal{G}(\alpha _{kM},1) \; ,$$

$$\text {and} \quad Z_i | {\varvec{\pi }} \sim \mathcal{M}(1, \pi _{1}, \ldots , \pi _{k}) \; ,$$

where ${\varvec{\varDelta }} _{\mathbf {w}_i} = \text {diag}(w_{i1}^{-1}, \ldots , w_{iM}^{-1})$, symbol $\otimes$ means that the components of $\mathbf {W}_{i}$ are independent and $\mathcal{M}(1, \pi _{1}, \ldots , \pi _{k})$ denotes the Multinomial distribution. In what follows, the weight variables will be denoted by $\mathbf {W}= \{\mathbf {W}_1, \ldots , \mathbf {W}_N\}$ and the labels by $\mathbf {Z}= \{Z_1, \ldots , Z_N\}$.

2.2 Priors on Parameters

In a Bayesian formulation, we assign priors on parameters in ${\varvec{\varPhi }}$. However, it is common (see e.g. [1]) not to impose priors on the parameters ${\varvec{\alpha }} _k$ since no convenient conjugate prior exist for these parameters. Then the scale matrix decomposition imposes that we set priors on ${\varvec{\mu }} _k$ and ${\varvec{D}} _k, {\varvec{A}} _k$. For the means ${\varvec{\mu }} _k$, the standard Gaussian prior can be used:

$$\begin{aligned} {\varvec{\mu }} _k \;|\; {\varvec{A}} _k, {\varvec{D}} _k\sim & {} \mathcal{N}({\varvec{m}} _k, {\varvec{D}} _k {\varvec{\varLambda }} _k^{-1} {\varvec{A}} _k^{-1} {\varvec{D}} _k^T) \;, \end{aligned}$$

(4)

where ${\varvec{m}} _k$ (vector) and ${\varvec{\varLambda }} _k$ (diagonal matrix) are hyperparameters and we shall use the notation ${\varvec{m}} =\{{\varvec{m}} _1, \ldots , {\varvec{m}} _K\}$ and ${\varvec{\varLambda }} =\{{\varvec{\varLambda }} _1, \ldots {\varvec{\varLambda }} _K\}$. For ${\varvec{A}} _k$ and ${\varvec{D}} _k$ a natural solution would be to use the distributions induced by the standard Wishart prior on ${\varvec{T}} _k$ but this appears not to be tractable in inference scheme based on a variational framework. The difficulty lies in considering an appropriate and tractable prior for ${\varvec{D}} _k$. There exists a number of priors on the Stiefel manifold among which a good candidate could be the Bingham prior and extensions investigated by [19]. However, it is not straightforward to derive from it a tractable E-${\varvec{\varPhi }} ^1$ step (see Sect. 2.3) that could provide a variational posterior distribution. Nevertheless, this kind of priors could be added in the M-${\varvec{D}}$-step. The simpler solution adopted in the present work consists of considering ${\varvec{D}} _k$ as an unknown fixed parameter and imposing a prior only on ${\varvec{A}} _k$, which is a diagonal matrix containing the positive eigenvalues of ${\varvec{T}} _k$. It is natural to choose:

$$\begin{aligned} {\varvec{A}} _k\sim & {} \otimes _{m=1}^M \mathcal{G}(\lambda _{km}, \delta _{km}) \;, \end{aligned}$$

(5)

where ${\varvec{\lambda }} _{k}=\{\lambda _{km}, m=1\ldots M\}$ and ${\varvec{\delta }} _{k}=\{\delta _{km}, m=1\ldots M\}$ are hyperparameters with ${\varvec{\lambda }} =\{{\varvec{\lambda }} _1, \ldots {\varvec{\lambda }} _K\}$ and ${\varvec{\delta }} =\{{\varvec{\delta }} _1, \ldots {\varvec{\delta }} _K\}$ as additional notation. It follows the joint prior on ${\varvec{\mu }} _{1:K} = \{{\varvec{\mu }} _1, \ldots , {\varvec{\mu }} _K\}$, ${\varvec{A}} _{1:K} = \{{\varvec{A}} _1, \ldots , {\varvec{A}} _K\}$ given ${\varvec{D}} _{1:K} = \{{\varvec{D}} _1, \ldots , {\varvec{D}} _K\}$

$$\begin{aligned} p({\varvec{\mu }} _{1:K}, {\varvec{A}} _{1:K} ; {\varvec{D}} _{1:K})= & {} \prod _{k=1}^K p({\varvec{\mu }} _k | {\varvec{A}} _k ; {\varvec{D}} _k) \; p( {\varvec{A}} _k) \end{aligned}$$

(6)

where the first term in the product is given by (4) and the second term by (5).

Then a standard Dirichlet prior $\mathcal{D}(\tau _1, \ldots , \tau _K)$ is used for the mixing weights ${\varvec{\pi }}$ with ${\varvec{\tau }} =\{\tau _1, \ldots , \tau _K\}$ the Dirichlet hyperparameters.

For the complete model, the whole set of parameters is denoted by ${\varvec{\varPhi }}$. ${\varvec{\varPhi }} =\{{\varvec{\varPhi }} ^1, {\varvec{\varPhi }} ^2\}$ is decomposed into a set ${\varvec{\varPhi }} ^1=\{{\varvec{\varPhi }} ^1_1, \ldots {\varvec{\varPhi }} ^1_K\}$ with ${\varvec{\varPhi }} ^1_k=\{{\varvec{\mu }} _k, {\varvec{A}} _k, \pi _k\}$ of parameters for which we have priors and a set ${\varvec{\varPhi }} ^2= \{{\varvec{\varPhi }} ^2_1, \ldots {\varvec{\varPhi }} ^2_K\}$ with ${\varvec{\varPhi }} ^2_k=\{{\varvec{D}} _k,{\varvec{\alpha }} _k\}$ of unknown parameters considered as fixed. In addition, hyperparameters are denoted by ${\varvec{\varPhi }} ^3=\{{\varvec{\varPhi }} ^3_1, \ldots {\varvec{\varPhi }} ^3_K\}$ with ${\varvec{\varPhi }} ^3_k=\{\tau _k, {\varvec{m}} _k, {\varvec{\varLambda }} _k, {\varvec{\lambda }} _k, {\varvec{\delta }} _k\}$.

2.3 Inference Using Variational Expectation-Maximization

The main task in Bayesian inference is to compute the posterior probability of the latent variables ${\varvec{X}} =\{{\varvec{W}}, {\varvec{Z}} \}$ and the parameter ${\varvec{\varPhi }}$ for which only the ${\varvec{\varPhi }} ^1$ part is considered as random. We are therefore interested in computing the posterior $p({\varvec{X}}, {\varvec{\varPhi }} ^1 \;|\; {\varvec{y}}, {\varvec{\varPhi }} ^2)$. This posterior is intractable and approximated here using a variational approximation $q({\varvec{X}}, {\varvec{\varPhi }} ^1)$ with a factorized form $q({\varvec{X}}, {\varvec{\varPhi }} ^1)= q_X({\varvec{X}}) \; q_{\varPhi ^1}({\varvec{\varPhi }} ^1)$ in the set $\mathcal{D}$ of product probability distributions. The so-called variational EM procedure (VEM) proceeds as follows. At iteration (r), the current parameters values are denoted by ${\varvec{\varPhi }} ^{2(r-1)}$ and VEM alternates between two steps,

$$\begin{aligned} {\mathbf{E \text {-}\mathbf{step {} \mathbf : }}}&\quad q^{(r)}({\varvec{X}}, {\varvec{\varPhi }} ^1) = \arg \max \limits _{ q \in \mathcal{D}} \mathcal{F}(q, {\varvec{\varPhi }} ^{2(r-1)}) \\ {\mathbf{M \text {-}\mathbf{step {} \mathbf : }}}&\quad {\varvec{\varPhi }} ^{2(r)} = \arg \max \limits _{ {\varvec{\varPhi }} ^2 } \mathcal{F}(q^{(r)}, {\varvec{\varPhi }} ^{2}) \; , \end{aligned}$$

where $\mathcal{F}$ is the usual free energy

$$\begin{aligned} \mathcal{F}(q, {\varvec{\varPhi }} ^{2})= & {} E_{q}[\log p({\varvec{y}}, {\varvec{X}}, {\varvec{\varPhi }} ^1; {\varvec{\varPhi }} ^2)] - E_{q}[\log q({\varvec{X}}, {\varvec{\varPhi }} ^1)]. \end{aligned}$$

(7)

The full expression of the free energy is not necessary to maximize it and to derive the variational EM algorithm. However, computing the free energy is useful. It provides a stopping criterion and a sanity check for implementation as the free energy should increase at each iteration. Then it can be used as specified in Sect. 3.1 as a replacement of the likelihood to provide a model selection procedure. Its detailed expression is given in a companion paper [2].

The E-step above divides into two steps. At iteration (r), denoting in addition by $q_X^{(r-1)}$ the current variational distribution for ${\varvec{X}}$:

$$\begin{aligned} {\mathbf{E }\text {-}{\varvec{\varPhi }} ^1\text {-}\mathbf{step {} \mathbf : } } \quad&q_{\varPhi ^1}^{(r)}({\varvec{\varPhi }} ^1) \propto \exp (E_{q^{(r-1)}_X}[\log p({\varvec{\varPhi }} ^1 | {\varvec{y}}, {\varvec{X}}; {\varvec{\varPhi }} ^{2(r-1)})]) \end{aligned}$$

(8)

$$\begin{aligned} {\mathbf{E }\text {-}\mathbf{X }\text {-}\mathbf{step {} \mathbf : } } \quad&q_X^{(r)}({\varvec{X}}) \propto \exp (E_{q^{(r)}_{\phi ^1}}[\log p({\varvec{X}} | {\varvec{y}}, {\varvec{\varPhi }} ^1 ; {\varvec{\varPhi }} ^{2(r-1)})]) \; . \end{aligned}$$

(9)

Then the M-step reduces to:

$$\begin{aligned} {\mathbf{M }\text {-}\mathbf{step {} \mathbf : }}&\quad \varPhi ^{2(r)} = \arg \max _{{\varvec{\phi }} ^2} E_{q^{(r)}_X q_{\varPhi ^1}^{(r)}}[\log p({\varvec{y}}, {\varvec{X}}, {\varvec{\varPhi }} ^1; {\varvec{\varPhi }} ^{2})] \; . \end{aligned}$$

The resulting variational EM algorithm is specified in [2] in two cases depending on the prior used for the mixing weights. For component elimination, the central quantity is $q_\pi ^{(r)}({\varvec{\pi }})$ the approximate variational posterior of ${\varvec{\pi }}$ that itself involves $q_Z^{(r)}({\varvec{Z}}) = \prod _i q_{Z_i}^{(r)}(Z_i)$ the variational posterior of the labels.

In what follows, we illustrate the use of this Bayesian formulation and its variational EM implementation on the issue of selecting the number of components in the mixture.

3 Single-Run Number of Component Selection

In this work, we consider approaches that start from an overfitting mixture with more components than expected in the data. In this case, as described by [16], identifiability will be violated in two possible ways. Identifiability issues can arise either because some of the components weights have to be zero (then component-specific parameters cannot be identified) or because some of the components have to be equal (then their weights cannot be identified). In practice, these two possibilities are not equivalent as checking for vanishing components is easier and is likely to lead to more stable behavior than testing for redundant components (see e.g. [27]).

Methods can be considered in a Bayesian and maximum likelihood setting. However, in a Bayesian framework, in contrast to maximum likelihood, considering a posterior distribution on the mixture parameters requires integrating out the parameters and this acts as a penalization for more complex models. The posterior is essentially putting mass on the sparsest way to approximate the true density, see e.g. [27]. Although the framework of [27] is fully Bayesian with priors on all mixture parameters, it seems that this penalization effect is also effective when only some of the parameters are integrated out. This is observed by [11] who use priors only for the component mean and covariance parameters. See [2] for details on the investigation of this alternative case with no prior on the mixing weights.

The idea of using overfitting finite mixtures with too many components K has been used in many papers. In a deliberately overfitting mixture model, a sparse prior on the mixture weights will empty superfluous components during estimation [21]. To obtain sparse solutions with regard to the number of mixture components, an appropriate prior on the weights ${\varvec{\pi }}$ has to be selected. Guidelines have been given in previous work when the prior for the weights is a symmetric Dirichlet distribution $\mathcal{D}(\tau _1, \ldots , \tau _K)$ with all $\tau _k$’s equal to a value $\tau _0$. To empty superfluous components automatically the value of $\tau _0$ has to be chosen appropriately. In particular, [27] proposed conditions on $\tau _0$ to control the asymptotic behavior of the posterior distribution of an overfitting mixture with respect to the two previously mentioned regimes. One regime in which a high likelihood is set to components with nearly identical parameters and one regime in which some of the mixture weights go to zero. More specifically, if $\tau _0 < d/2$ where d is the dimension of the component specific parameters, when N tends to infinity, the posterior expectation of the weight of superfluous components converges to zero. In practice, N is finite and as observed by [21], much smaller value of $\tau _0$ are needed (e.g. $10^{-5}$). It was even observed by [29] that negative values of $\tau _0$ were useful to induce even more sparsity when the number of observations is too large with respect to the prior impact. Dirichlet priors with negative parameters, although not formally defined, are also mentioned by [13]. This latter work does not start from a Bayesian formulation but is based on a Minimum Message Length (MML) principle. [13] provide an M-step that performs component annihilation, thus an explicit rule for moving from the current number of components to a smaller one. A parallel is made with a Dirichlet prior with $\tau _0= - d/2$ which according to [29] corresponds to a very strong prior sparsity.

In a Bayesian setting with symmetric sparse Dirichlet priors $\mathcal{D}(\tau _0, \ldots , \tau _0)$, the theoretical study of [27] therefore justifies to consider the posterior expectations of the weights $E[\pi _k | {\varvec{y}} ]$ and to prune out the too small ones. In practice this raises at least two additional questions: which expression to use for the estimated posterior means and how to set a threshold under which the estimated means are considered too small. The posterior means estimation is generally guided by the chosen inference scheme. For instance in our variational framework with a Dirichlet prior on the weights, the estimated posterior mean $E[\pi _k | {\varvec{y}} ]$ takes the following form (the (r) notation is removed to signify the convergence of the algorithm),

$$\begin{aligned} E[\pi _k | {\varvec{y}} ]\approx & {} E_{q_{\varvec{\pi }}}[\pi _k] = \frac{\tilde{\tau }_k}{\sum _{l=1}^K \tilde{\tau }_l} \nonumber \\= & {} \frac{\tau _k + n_k}{ \sum _{k=1}^K \tau _k + N} \end{aligned}$$

(10)

where $n_k= \sum _{i=1}^N q_{Z_i}(k)$ and the expression for $q_{Z_i}(k)$ is detailed in [2]. If we are in the no weight prior case, then the expectation simplifies to

$$\begin{aligned} \pi _k\approx & {} \frac{ n_k}{ N} \end{aligned}$$

(11)

with the corresponding expression of $q_{Z_i}(k)$ also given in [2].

Nevertheless, whatever the inference scheme or prior setting, we are left with the issue of detecting when a component can be set as empty. There is usually a close relationship between the component weight $\pi _k$ and the number of observations assigned to component k. This later number is itself often replaced by the sum $n_k= \sum _{i=1}^N q_{Z_i}(k)$. As an illustration, the choice of a negative $\tau _0$ by [13] corresponds to a rule that sets a component weight to zero when $n_k=\sum _{i=1}^N q_{Z_i}(k)$ is smaller than d/2. This prevents the algorithm from approaching the boundary of the parameter space. When one of the components becomes too weak, meaning that it is not supported by the data, it is simply annihilated. One of the drawbacks of standard EM for mixtures is thus avoided. The rule of [13] is stronger than that used by [22] which annihilates a component when the sum $n_k$ reduces to 1 or the one of [11] which corresponds to the sum $n_k$ lower than a very small fraction of the sample size, i.e. $\sum _{i=1}^N q_{Z_i}(k)/N < 10^{-5}$ where N varies from 400 to 900 in their experiments. Note that [22] use a Bayesian framework with variational inference and their rule corresponds to thresholding the variational posterior weights (10) to 1/N because they set all $\tau _k$ to 0 in their experiments.

In addition to these thresholding approaches, alternatives have been developed that would worth testing to avoid the issue of setting a threshold for separating large and small weights. In their MCMC sampling, [21] propose to consider the number of non-empty components at each iteration and to estimate the number of components as the most frequent number of non-empty components. This is not directly applicable in our variational treatment as it would require to generate hard assignments to components at each iteration instead of dealing with their probabilities. In contrast, we could adopt techniques from the Bayesian non parametrics literature which seek for optimal partitions, such as the criterion of [12] using the so-called posterior similarity matrix ([15]). This matrix could be approximated easily in our case by computing the variational estimate of the probability that two observations are in the same component. However, even for moderate numbers of components, the optimization is already very costly.

In this work, we consider two strategies for component elimination. The first one is a thresholding approach while the second one is potentially more general as it is based on increasing the overall fit of the model assessed via the variational free energy at each iteration. Also it avoids the choice of a threshold for separating between large or small weights. The tested procedures are more specifically described in the next section.

3.1 Tested Procedures

We compare two single-run methods to estimate the number of components in a mixture of multiple scale distributions.

Thresholding Based Algorithm: A first method is directly derived from a Bayesian setting with a sparse symmetric Dirichlet prior likely to induce vanishing coefficients as supported by the theoretical results of [27]. This corresponds to the approach adopted in [21] and [22]. The difference between the later two being how they check for vanishing coefficients. Our variational inference leads more naturally to the solution of [22] which is to check the weight posterior means, that is whether at each iteration (r),

$$\begin{aligned} n^{(r)}_k< & {} (K \tau _0 + N) \rho _t -\tau _0 \end{aligned}$$

(12)

where $\rho _t$ is the chosen threshold on the posterior means. When $\rho _t$ is set such that (12) leads to $n^{(r)}_k < 1$, this method is referred to, in the next Section, as SparseDirichlet+$\pi$test. For comparison, the algorithm run with no intervention is called SparseDirichlet.

Free Energy Based Algorithm: We also consider a criterion based on the free energy (7) to detect components to eliminate. This choice is based on the observation that when we cannot control the hyperparameters (e.g $\tau _k$) to guide the algorithm in the vanishing components regime, the algorithm may as well go to the redundant component regime. The goal is then to test whether this alternative method is likely to handle this behavior. The proposal is to start from a clustering solution with too many components and to try to remove them using a criterion based on the gain in free energy. In this setting, the components that are removed are not necessarily vanishing components but can also be redundant ones. In the proposed variational EM inference framework, the free energy arises naturally as a selection criterion. It has been stated in [4] and [8] that the free energy penalizes model complexity and that it converges to the well known Bayesian Information Criterion (BIC) and Minimum Description Length (MDL) criteria, when the sample size increases, illustrating the interest of this measure for model selection.

The free energy expression used is given in [2]. The heuristic denoted by SparseDirichlet+FEtest can be described as follows (see the next section for implementation details).

• 1. Iteration $r = 0$: Initialization of the $K^{(0)}$ clusters and probabilities using for instance repetitions of k-means or trimmed k-means.

• 2. Iteration $r \ge 1$:

  • (a) E and M steps updating from parameters at iteration $r - 1$

  • (b) Updating of the resulting Free Energy value

  • (c) In parallele, for each cluster $k \in \{ 1 \ldots K^{(r-1)} \}$

    • i. Re-normalization of the cluster probabilities when cluster k is removed from current estimates at iteration $r-1$: the sum over the remaining $K^{(r-1)}-1$ clusters must be equal to 1

    • ii. Updating of the corresponding E and M steps and computation of the associate Free Energy value

  • (d) Selection of the mixture with the highest Free Energy among the $K^{(r-1)}$-component mixture (step (b)) or one of the $(K^{(r-1)}-1)$-component mixtures (step (c)).

  • (e) Updating of $K^{(r)}$ accordingly, to $K^{(r-1)}$ or $K^{(r-1)}-1$ .

• 3. When no more cluster deletion occur (eg. during 5 steps), we switch to the EM algorithm (SparseDirichlet).

4 Experiments

In addition to the 3 methods SparseDirichlet+$\pi$test, SparseDirichlet+FEtest and SparseDirichlet, referred to below as $\mathcal{MP}$ single-run procedures, we consider standard Gaussian mixtures using the Mclust package [28] including a version with priors on the means and covariance matrices. The Bayesian Information Criterion (BIC) is used to select the number of components from $K=1$ to 10. The respective methods are denoted below by GM+BIC and Bayesian GM+BIC. Regarding mixtures of $\mathcal{MP}$ distributions, we also consider their non Bayesian version, using BIC to select K, denoted below by MMP+BIC.

In practice, values need to be chosen for hyperparameters. These include the ${\varvec{m}} _k$ that are set to 0, the ${\varvec{\varLambda }} _k$ that are set to $\epsilon {\varvec{I}} _M$ with $\epsilon$ small (set to $10^{-4}$) so has to generate a large variance in (4). The $\delta _{km}$ are then set to 1 and $\lambda _{km}$ to values $5\times 10^{-4}=\lambda _1< \lambda _2< \ldots < \lambda _M = 10^{-3}$. The $\tau _k$’s are set to $10^{-3}$ to favor sparse mixtures.

Initialization is also an important step in EM algorithms. For one data sample, each single-run method is initialized $I=10$ times. These $I=10$ initializations are the same for all single-run methods. Each initialization is obtained with $K=10$ using trimmed k-means and excluding 10% of outliers. Each trimmed kmeans output is the one obtained after running the algorithm from $R= 10$ restarts and selecting the best assignment after 10 iterations. For each run of a procedure (data sample), the $I=10$ initializations are followed by 5000 iterations maximum of VEM before choosing the best output. For Gaussian mixtures, the initialization procedure is that embedded in Mclust. For $\mathcal{MP}$ models, initial values of the $\alpha _{km}$’s are set to 1.

Another important point for single-run procedures, is how to finally enumerate remaining components. For simplicity, we report components that are expressed by the maximum a posteriori (MAP) rule, which means components for which there is at least one data point assigned to them with the highest probability.

Table 1. 13 models simulated 10 times each: the true number of components is varying so the columns indicate the difference between the selection and the truth. The average time (for the total of the $I=10$ repetitions, over the 130 samples) is indicated in the last column. The most frequent selection (in %) is indicated by a box while the true value is in green.

Fig. 1.

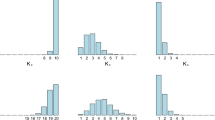
Examples of simulated samples. First line: 3 Gaussian mixtures with 3 and 5 components. Second line: $\mathcal{MP}$ mixtures with different dof and increasing separation from left to right. Third line: $\mathcal{MP}$ mixtures with increasing separation, from left to right, and increasing number of points, $N=900$ for the first plot, $N=9000$ for the last two.

Fig. 2.

Illustration of the two component elimination strategies: Free energy gain strategy, iterations 10 to 50 (left) and too small component proportion test, iterations 10 to 720 (right). Eliminations are marked with red lines. Most of them occur at earlier iterations when using the free energy test.

4.1 Simulated Data

We consider several models (more details can be found in [2]), 3 Gaussian mixtures and 10 $\mathcal{MP}$ mixtures, with 10 simulated samples each, for a total of 130 samples, K varying from 3 to 5, N from 900 to 9000, with close or more separated clusters. The results are summarized in Table 1 and the simulated samples illustrated in Fig. 1. Gaussian mixture models provide the right component number in 26% to 32% of the cases, which is higher than the number of Gaussian mixtures in the test (23%). All procedures hesitate mainly between the true number and this number plus 1. We observe a good behavior of the free energy heuristic with a time divided by 3 compared to the non Bayesian $\mathcal{MP}$ mixture procedure, although the later benefits from a more optimized implementation. For the first strategy, the dependence to the choice of a threshold value is certainly a limitation although some significant gain is observed over the cases with no component elimination (SparseDirichlet line in Table 1). Overall, eliminating components on the run is beneficial, both in terms of time and selection performance but using a penalized likelihood criterion (free energy) to do so avoid the commitment to a fix threshold and is more successful. A possible reason is that small components are more difficult to eliminate than redundant ones. Small components not only require the right threshold to be chosen but also they may appear at much latter iterations as illustrated in Fig. 2.

5 Discussion and Conclusion

We investigated, in the context of mixtures of non-Gaussian distributions, different single-run procedures to select automatically the number of components. The Bayesian formulation makes this possible when starting from an overfitting mixture, where K is larger than the expected number of components. The advantage of single run procedures is to avoid time consuming comparison of scores for each mixture model from 1 to K components. There are different ways to implement this idea: full Bayesian settings which have the advantage to be supported by some theoretical justification [27] and Type II maximum likelihood as proposed by [11] (not reported here but investigated in [2]). For further acceleration, we investigated component elimination which consists of eliminating components on the run. They are two main ways to do so: components are eliminated as soon as they are not supported by enough data points (their estimated weight is under some threshold) or when their removal does not penalize the overall fit. For the latest case, we proposed a heuristic based on the gain in free energy. The free energy acts as a penalized likelihood criterion and can potentially eliminate both too small components and redundant ones. Redundant components do not necessarily see their weight tend to zero and cannot be eliminated via a simple thresholding.

As non Gaussian components, we investigated in particular the case of multiple scale distributions [14], which have been shown to perform well in the modelling of non-elliptical clusters with potential outliers and tails of various heaviness. We proposed a Bayesian formulation of mixtures of such multiple scale distributions and derived an inference procedure based on a variational EM algorithm to implement the single-run procedures.

On preliminary experiments, we observed that eliminating components on the run is beneficial, both in terms of time and selection performance. Free energy based methods appeared to perform better than posterior weight thresholding methods: using a penalized likelihood criterion (free energy) avoids the commitment to a fix threshold and is not limited to the removal of small components. However, a fully Bayesian setting is probably not necessary as both in terms of selection and computation time, Type II maximum likelihood on the weights was competitive with the use of a Dirichlet prior with a slight advantage to the latter (results reported in [2]).

To confirm these observations, more tests on larger and real data sets would be required to better compare and understand the various characteristics of each procedure. Theoretical justification for thresholding approaches, as provided by [27], applies for Gaussian mixtures but may not hold in our case of non-elliptical distributions. A more specific study would be required and could provide additional guidelines as how to set the threshold in practice. Also time comparison in our study is only valid for the Bayesian procedures for which the implementation is similar while the other methods using BIC have been better optimized, but this does not change the overall conclusion as regards computational efficiency.