33.1 Introduction

It is known that nanoparticles (NPs) are a particle with a size ranged from 1 to 100 nm, at least for one dimension [1]. NPs are already shown perspective biological and physicochemical properties [2,3,4]. Nowadays, they start to be widely used in nanoelectronics as a part of sensors and optoelectronic devices [5, 6]. Initially, the main focus of scientists was directed on the synthesis and investigation of NPs that contained single structures, termed simple NPs. Silver and gold are the most representative among simple NPs due to their unique features and utilization [7,8,9].

The progress in materials science has helped scientists to design a new class of NPs known as hybrid NPs, which can be defined as well-organized nanomaterials consisting of two, three or more types of single nanocomponents [10]. NPs with a core-shell structure is a kind of hybrid NPs that are composed of two or more nanomaterials, where an inner core surrounded by one shell of a different material. Among hybrid NPs, the investigation of bimetallic NPs composed of two different metal elements increasingly gathers steam [11]. Recent research had shown that bimetallic nanoparticles sometimes can be a preferable choice over a monometallic, due to their superior properties [12,13,14]. Electronic properties of the metallic nanoparticles are strongly depending on particle size [15], structure and compound. Therefore, the controlling of the fabrication process, atomic compound and temperature stability of the nanoparticles are important problems of modern nanotechnology. Numerous methods of synthesis of nanoparticles with different structures, size and shape were suggested in many works [5, 12]. However, some experimental techniques that are widely used in materials science, not always can be used for investigation of the structure and behavior of the nanoscale objects [4]. Hence, various theoretical [16,17,18] and computational [19,20,21,22] investigations can be an additional tool in studying nanostructures.

The researchers have noted that for fcc metals among all crystallographic planes that terminate the nanocrystal surface, high index facets demonstrate excellent activity and selectivity for chemical reactions compared with low index facets [23,24,25,26,27]. Therefore, silver nanoparticle structures with different sizes are of great scientific and research interest.

33.2 Model

In this paper, we present the investigation of the melting behavior of silver nanoparticles with spherical shape and different diameters by classical molecular dynamics simulation. The snapshots that represent the size variation of Ag NPs were prepared using Visual Molecular Dynamics software [28] and shown in Fig. 33.1.

Fig. 33.1
figure 1

Example of the studied silver nanoparticles with diameter of the NP equal to 4.8, 11.4, and 24.5 nm from left to right

Full size image

Silver atoms were placed at initial positions according to the Ag face-centered cubic lattice. Ideal vacuum conditions were maintained during the simulation. Free boundary conditions were applied in all three directions. The initial diameter of the nanoparticle varies from 4.8 to 24.5 nm with the number of particles (N) involved in simulation from 3589 to 452,221 atoms. The embedded atom method (EAM) was chosen to describe the interaction between atoms [29]. The generalized EAM potential is widely used in MD simulation of metal alloys and well fitted to reproduce the basic material properties. Within the EAM approach, the potential energy of the metal crystal is expressed as follows:

$$ E = \frac{1}{2}\sum\limits_{i,j,i \ne j} {\varphi \left( {r_{ij} } \right)} + \sum\limits_{i} {F\left( {\rho_{i} } \right)} , $$
(33.1)

where \( \varphi \left( {r_{ij} } \right) \) is the pair energy between atoms i and j at the distance \( r_{ij} \), F(ρi) is the local embedded energy of the atom i with electron density ρi.

Each term in (33.1) has the analytical expression that was proposed by approximating the data obtained from the calculations from the first principles. Thus, the pair energy of the interatomic interaction has the form

$$ \begin{aligned} \varphi \left( r \right) & = \frac{{A \cdot \exp \left[ { - \alpha \left( {\frac{r}{{r_{e} }} - 1} \right)} \right]}}{{1 + \left( {\frac{r}{{r_{e} }} - \kappa } \right)^{20} }} \\ & \quad - \frac{{B \cdot \exp \left[ { - \beta \left( {\frac{r}{{r_{e} }} - 1} \right)} \right]}}{{1 + \left( {\frac{r}{{r_{e} }} - \lambda } \right)^{20} }}, \\ \end{aligned} $$
(33.2)

where re—the equilibrium distance between the two atoms of the given type; A, B, α, β—approximation parameters; κ, λ—additional parameters for ensuring zero energy of interaction at significant interatomic distances.

The local embedding energy as a function of electron density F(ρi) is calculated in several steps. First, the electronic density ρi is calculated as

$$ \rho_{i} = \sum\limits_{i,j \ne i} {f\left( {r_{ij} } \right)} , $$
(33.3)

where f(rij)—local electron density in the atomic region of atom i, calculated through the following expression

$$ f\left( r \right) = \frac{{f_{e} \cdot \exp \left[ { - \beta \left( {\frac{r}{{r_{e} }} - 1} \right)} \right]}}{{1 + \left( {\frac{r}{{r_{e} }} - \lambda } \right)^{20} }}, $$
(33.4)

that has the same form as the second term in formula (33.2) with the same parameter values β and λ. Then the electronic density function F(ρi) should be calculated, from three following equations, depending on the value of ρi,

$$ F\left( \rho \right) = \sum\limits_{i = 0}^{3} {F_{ni} \left( {\frac{\rho }{{\rho_{n} }} - 1} \right)^{i} } ,\rho < \rho_{n} ,\rho_{n} = 0,85\rho_{e} , $$
(33.5)
$$ F\left( \rho \right) = \sum\limits_{i = 0}^{3} {F_{i} \left( {\frac{\rho }{{\rho_{e} }} - 1} \right)^{i} } ,\rho_{n} \le \rho < \rho_{0} ,\rho_{0} = 1,15\rho_{e} , $$
(33.6)
$$ F(\rho ) = F_{e} \left[ {1 - \ln \left( {\frac{\rho }{{\rho_{e} }}} \right)^{\eta } } \right] \cdot \left( {\frac{\rho }{{\rho_{e} }}} \right)^{\eta } ,\rho_{0} \le \rho . $$
(33.7)

Such a method for determining the electronic density function F(ρi) is necessary for the realistic approximation of the embedding energy, and for reproducing the properties of the material in a wide range of values ρ.

To find the analytical expressions and numerical parameters for the functions used in expressions (33.1) and (33.2) refers to work [29].

To investigate the melting behavior of the nanoparticles the Lindemann index [28] that is a measure of the thermally driven disorder of atoms was computed. The local Lindemann index of an atom i can be defined as:

$$ q_{i} = \frac{1}{N - 1}\sum\limits_{j \ne i} {\frac{{\sqrt {\left\langle {r_{ij}^{2} } \right\rangle - \left\langle {r_{ij} } \right\rangle^{2} } }}{{\left\langle {r_{ij} } \right\rangle }}} $$
(33.8)

where angle brackets indicate time average at a constant temperature.

General Lindemann index for a system of N atoms can be estimated through averaging over all atoms in the sample. As it is known, with increasing of the sample’s temperature, the Lindemann index growth linearly till the sharp threshold, which is close to the melting point [30]. This threshold can be considered as an indication of the crystal-amorphous phase transition. For bulk sample, the critical value of the Lindemann index which can be considered as melting criteria is expected to be in the range from 0.1 to 0.15, depending on the type of the materials [22]. However, recent research [22] had shown that melting of the nanoparticle may occur at the much smaller value of a Lindemann index \( q_{c} \) in the range from 0.03 to 0.05.

During the simulation, the system temperature was increased consequentially using Berendsen thermostat [31] from 300 to 2500 K.

The computational code is implemented using algorithms from LLAMPS software package [32].

33.3 Results

It is worth to mention that calculation of the Lindemann index for very large samples requires significant computational time. Thus in present work temperature dependences of the Lindemann indexes were calculated for silver nanoparticles with diameter from 4.8 to 13.0 nm. Obtained dependences are shown in Fig. 33.2. As can be seen from the figure, presented dependence exhibits typical behavior, slightly increasing in the pre-melting region, with the threshold where it exceeds the critical value around 1000 K for smallest NP a slightly shifting right up to approximately 1200 K for the sample with diameter 13.0 nm. With further temperature growth, Lindemann index continues to increase, and nanoparticle became completely melted above 1100–1400 K for smallest and largest NP radius respectively.

Fig. 33.2
figure 2

Temperature dependence of the Lindemann index of the silver nanoparticles with different diameter

Full size image

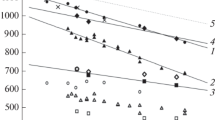
To investigate the melting behavior of the silver NP of larger sizes and to validate obtained results, temperature dependencies of the averaged potential energy of the studied samples, also were calculated (Fig. 33.3). Dependencies presented in Fig. 33.3 also show typical for the melting process behavior with regions of slow growth prior to melting and rapid increasing as the melting starts.

Fig. 33.3
figure 3

Temperature dependence of the average potential energy of the silver nanoparticles with different diameter (curves are shifted vertically for clearance)

Full size image

The snapshots of the typical atomistic configuration of three nanoparticles with a diameter of 4.8, 11.4, and 24.5 nm at different temperatures values are shown in Fig. 33.4. As it follows from visual analysis of the general views of nanoparticle, the heating leads to the rearrangement of the atoms from their initial FCC crystal structure to almost amorphous. At temperatures of approximately 1200 K, the longitudinal order in the crystalline structure of the samples begins to collapse and at temperatures above 2250 K, the melting processes intensively occur in the samples, causing the destruction of the crystalline structure.

Fig. 33.4
figure 4

Atomistic configurations of the Ag nanoparticles with diameter 4.8, 11.4, and 24.5 nm from top to bottom. Temperature of the snapshots from left to right: 900, 1200 and 2250 K

Full size image

To detect the changes in the structure of NP’s depending on the size of the sample the radial distribution functions \( g(r) \) [33] were calculated at temperature of 1500 K for nanoparticles with diameter 4.8, 11.4, and 24.5 nm (Fig. 33.5).

Fig. 33.5
figure 5

Radial distribution functions for silver nanoparticles with diameter 4.8, 11.4, and 24.5 nm at temperature 1500 K

Full size image

As can be seen from the figure, in RDF obtained at the same temperature intensity of fluctuations is decreasing with the growth of the size of nanoparticle. This may indicate that at the same temperature nanoparticle with smaller radius have more amorphous regions comparing to larger ones. This situation was also observed in temperature dependences of Lindemann index and potential energy (see Figs. 33.2 and 33.3).

As was reported in literature [6] melting of the silver nanoparticle of spherical shape starts at surface. To detect this feature in studied samples we plot the atomistic configuration of spatial distribution of the atoms on Lindemann index within the volume of the sample around melting temperature at 1280 К (Fig. 33.6). As can be seen from figure, most of the atoms in the middle section of the sample are characterized by close values of the Lindemann indexes, around value of \( q{ \approx }0.01 \), while some atoms in the center of the nanoparticle have slightly higher value of Lindemann index.

Fig. 33.6
figure 6

Spatial distribution of the atoms on Lindemann index within the volume of the sample at T 1280 К for NP with diameter 13.0 nm. Atoms with different values of Lindemann index are shown in different colors according to scale

Full size image

At the same time, atoms on the surface of nanoparticle are characterized by values of Lindemann index from the whole range, many of which are higher than atoms in middle section. Thus, some atoms on the surfaces move more intensively, comparing to atoms within the volume of the sample, and melting is expected to occur on surface first.

To validate this assumption, we plot atomistic configuration of the largest nanoparticle with a diameter nanoparticle 24.5 nm at 1400 K with visible interatomic spaces (Fig. 33.7).

Fig. 33.7
figure 7

Cross-section of the structure of the silver NP with diameter of 24.5 nm at 1400 (note the amorphous structure on the surface)

Full size image

As Fig. 33.7 shows, the process of thermal destruction of the crystal lattice start at the surfaces of the samples and at the beginning of the melting, long-range ordering is preserved at the center of nanoparticles.

33.4 Conclusions

Melting behavior of the silver nanoparticles with spherical shape and of the different radius was investigated by classical molecular dynamics simulations. To detect the structural changes in the atomic configuration of the nanoparticles the temperature dependencies of Lindemann indexes were calculated for six samples and average potential energies were calculated for all samples in the range from 300 K to 2500 K. As it follows from the computed parameters, the melting of the considered nanoparticles occurred at temperatures of about 1000 K for smallest NP, shifting to higher values with the growth of NP size. At that point, the Lindemann index exceeds the critical value and increasing rapidly with temperature growth, as well as the average energy. As it follows from the snapshots of atomistic configurations, and distribution of atoms on Lindemann index within the volume of the sample thermal destruction of the FCC crystal structure of spherical silver nanoparticles begins at the surface, as the atoms located in outmost from center layers lose their long-range ordering. Then, with the temperature growth, thermal degradation propagates to the center of the samples. This situation was observed for all studied nanoparticles of different diameters.