On an Algebraic Analogue of the Mayer–Vietoris Sequence

Abstract

We prove an algebraic analogue of the Mayer–Vietoris sequence for cohomology for the part of the sequence corresponding to the zeroth and first cohomology. We also prove a result which gives an indication of how one should continue this sequence to include the second cohomology groups in the case of rings of dimension 2.

1 Introduction

Let X be a topological space, $H^0(X,\mathbb {Z})$ be the set of continuous maps from X to $\mathbb {Z}$ and $H^1(X,\mathbb {Z})$ be the set of all homotopy classes of continuous maps from X to $S^1$. Since $\mathbb {Z}$ and $S^1$ are abelian groups, $H^0(X,\mathbb {Z})$ and $H^1(X,\mathbb {Z})$ are also abelian groups. In the literature, the group $H^1(X,\mathbb {Z})$ is known as Bruschlinsky group (for details one can see [5]).

Theorem 15.1

Let $U_1$ and $U_2$ be two open sets of a topological space X. Then we have an exact sequence

$$\begin{aligned}&H^0(U_1\cup U_2, \mathbb {Z})\rightarrow H^0(U_1, \mathbb {Z})\oplus H^0(U_2, \mathbb {Z})\rightarrow H^0(U_1\cap U_2, \mathbb {Z}){\rightarrow } H^1(U_1\cup U_2, \mathbb {Z}) \\&\rightarrow H^1(U_1, \mathbb {Z})\oplus H^1(U_2, \mathbb {Z})\rightarrow H^1(U_1\cap U_2, \mathbb {Z}). \end{aligned}$$

This sequence is known as Mayer–Vietoris sequence.

We refer the reader to see the book of Wall [12] for the definitions and the construction of the Mayer–Vietoris sequence. It is natural to ask that ‘Does there exist an algebraic analogue of Mayer–Vietoris sequence?’ The main aim of this paper is to define two algebraic groups ${\Gamma }(A)$ and $\pi _1 (\mathrm{SL}_2 (A))$, where A is an integral domain and also to prove an algebraic analogue of Mayer–Vietoris sequence with the help these groups for an integral domain of dimension 1. The group $\Gamma (A)$ is also discussed by Krusemeyer ([7]) in different context.

By using the theory of symplectic modules, we also give an algebraic analogue of the connecting homomorphism

$$\begin{aligned} H^1(U_1\cap U_2,\mathbb {Z}) \rightarrow H^2(U_1\cup U_2,\mathbb {Z}). \end{aligned}$$

(15.1)

This paper is organized as follows. After recalling some preliminary results in Sect. 15.2, we give an analogue of Theorem 15.1 in Sects. 15.3 and 15.4. In Sect. 15.5, we give an analogue of the map (15.1) and finally in Sect. 15.6, we deduce some corollaries of our results.

2 Some Preliminaries

In this section, we give some definitions and preliminary results. Throughout the paper, ring A means commutative ring with identity.

Definition 15.1

• 1. Let A be a ring. A row $(a_1,a_2,\ldots ,a_n)\in A^{n}$ is said to be unimodular (of length n) if the ideal $(a_1,a_2,\ldots ,a_n) = A$. The set of unimodular rows of length n is denoted by $\mathrm{Um}_n(A)$.

• 2. A unimodular row $(a_1,a_2,\ldots ,a_n)$ is said to be completable if there is a matrix in $\mathrm{SL}_n(A)$ (or in $\mathrm{GL}_n(A)$) whose first row (or first column) is $(a_1,a_2,\ldots ,a_n)$.

• 3. We define $E_n(A)$ to be the subgroup of $\mathrm{GL}_n(A)$ generated by all matrices of the form $E_{ij}(\lambda )=I_n+\lambda e_{ij}, \lambda \in A, i \ne j$, where $e_{ij}$ is a matrix whose (i, j)th entry is 1 and all other entries are 0. The matrices $E_{ij}(\lambda )$ will be referred to as elementary matrices.

We now define the symplectic and elementary symplectic group of a ring. Let $e_{ij}$ be the matrix with 1 in the (i, j) place and zeros elsewhere, $e_i$ the ith row of $I_n$, and

$$\chi _r = \sum _{i=1}^{r}e_{2i-1,2i} - \sum _{i=1}^{r}e_{2i,2i-1}.$$

We display the case $r = 2$ explicitly below.

$$\begin{aligned} \chi _2= & {} \sum _{i=1}^{2}e_{2i-1,2i} - \sum _{i=1}^{2}e_{2i,2i-1}\\= & {} e_{12}+e_{34}-e_{21}-e_{43}\\= & {} \begin{pmatrix} 0&{}1&{}0&{}0\\ -1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}-1&{}0 \end{pmatrix}. \end{aligned}$$

Definition 15.2

The group of symplectic matrices $\mathrm{Sp}_{2r}(A)$ is given by

$$ \mathrm{Sp}_{2r}(A) = \{\alpha \in \mathrm{GL}_{2r}(A):\alpha ^{t}\chi _{r}\alpha = \chi _{r}\}, $$

which is clearly a subgroup of of $\mathrm{GL}_{2r}(A)$.

In order to define the elementary symplectic matrices, we use the permutation $\sigma$ on 2r-letters given by

$$ \sigma (2i) = 2i-1\; \text {and}\;\sigma (2i-1) = 2i,\;\text {for}\; 1 \le i \ne j \le 2r. $$

Definition 15.3

• 1. For each pair $i\ne j$ ($1 \le i \ne j \le 2r$) the elementary symplectic matrix $se_{ij}(z)$ is given by

  $$ se_{ij}(z) = {\left\{ \begin{array}{ll} I_{2r} + z\cdot e_{ij}&{}\text {if}\;\; i = \sigma j \\ I_{2r} + z\cdot e_{ij} - (-1)^{i+j}\cdot z\cdot e_{\sigma j,\sigma i}&{}\text {if}\;\; i \ne \sigma j \;\;\text {and} \;\;i < j. \end{array}\right. } $$

  We shall call these matrices elementary symplectic.

• 2. The group $\mathrm{ESp}_{2r}(A)$ is then the subgroup of $\mathrm{Sp}_{2r}(A)$ generated by the elementary symplectic matrices over A.

For the case $r = 2$, there are eight such matrices, the matrix $se_{13}(z)$ ($i\ne \sigma (j)$) is displayed below.

$$ \begin{pmatrix} 1&{}0&{}z&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}-z&{}0&{}1 \end{pmatrix}. $$

For the other three cases, the positions of $\pm {z}$ change accordingly. Likewise for $r = 2$ the matrix $se_{43}(z)$ ($i = \sigma (j)$) is displayed below.

$$ \begin{pmatrix} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}z&{}1 \end{pmatrix}. $$

For the other three cases, the positions of z change accordingly.

Let us recall Quillen’s Splitting Lemma [8] with the proof following the exposition of [3]. In what follows, $(\psi _1(X))_t$ denotes the image of $\psi _1(X)$ in $\mathrm{SL}_n(A_{st}[X])$ and $(\psi _2(X))_s$ denotes the image of $\psi _2(X)$ in $\mathrm{SL}_n(A_{st}[X])$.

Lemma 15.1

(see [8]) Let A be a domain and $s,t\in A$ be such that $sA + tA = A$. Suppose there exists $\sigma (X)\in \mathrm{SL}_n(A_{st}[X])$ with the property that $\sigma (0) = I_n$. Then there exist $\psi _1(X)\in \mathrm{SL}_n(A_{s}[X])$ with $\psi _1(0) = I_n$ and $\psi _2(X)\in \mathrm{SL}_n(A_{t}[X])$ with $\psi _2(0) = I_n$ such that $\sigma (X) = (\psi _1(X))_t(\psi _2(X))_s$.

Proof

Since $\sigma (0) = I_n$, $\sigma (X) = I_n + X\tau (X)$, where $\tau (X)\in M_n(A_{st}[X])$, we choose a large integer $N_1$ such that $\sigma (\lambda s^kX)\in \mathrm{SL}_n(A_t[X])$ for all $\lambda \in A$ and for all $k\ge N_1$. Define $\beta (X,Y,Z)\in \mathrm{SL}_n(A_{st}[X,Y,Z])$ as follows:

$$\begin{aligned} \beta (X,Y,Z) = \sigma ((Y+Z)X)\sigma (YX)^{-1}. \end{aligned}$$

(15.2)

Then $\beta (X,Y,0) = I_n$, and hence there exists a large integer $N_2$ such that for all $k\ge N_2$ and for all $\mu \in A$ we have $\beta (X,Y,\mu t^kZ)\in \mathrm{SL}_n(A_{s}[X,Y,Z])$. This means

$$\begin{aligned} \beta (X,Y,\mu t^kZ) = (\sigma _1(X,Y,Z))_t, \end{aligned}$$

(15.3)

where $\sigma _1(X,Y,Z)\in \mathrm{SL}_n(A_{s}[X,Y,Z])$ with $\sigma _1(X,Y,0) = I_n$.

Taking $N = \text {max}(N_1,N_2)$, it follows by the comaximality of sA and tA that $s^NA + t^NA = A$. Pick $\lambda ,\mu \in A$ such that $\lambda s^N + \mu t^N = 1$. Setting $Y = \lambda s^N$, $Z = \mu t^N$ in (15.2) and $Z = 1$, $Y = \lambda s^N$ in (15.3) we get

$$\beta (X,\lambda s^N,\mu t^N) = \sigma (X)\sigma (\lambda s^NX)^{-1}$$

and

$$\beta (X,\lambda s^N,\mu t^N) = (\sigma _1(X,\lambda s^N,\mu t^N))_t = (\psi _1(X))_t,\; \text {where} \;\psi _1(X)\in \mathrm{SL}_n(A_{s}[X]).$$

Hence, we conclude $\sigma (X)\sigma (\lambda s^NX)^{-1} = (\psi _1(X))_t$. Let $\sigma (\lambda s^NX) = (\psi _2(X))_s$, where $(\psi _2(X))_s\in \mathrm{SL}_n(A_{t}[X])$. Since $\sigma (0) = I_n$, $\psi _1(0) = \psi _2(0) = I_n$, the result follows by using the identity $\sigma (X) = \sigma (X)\sigma (\lambda s^NX)^{-1}\sigma (\lambda s^NX)$.

Lemma 15.2

([4]) Let A be a domain and $s,t\in A$ be such that $sA + tA = A$. For each $\sigma \in \mathrm{SL}_n(A_{st})$ and $\varepsilon \in E_n(A_{st})$ there exist $\tau _1\in \mathrm{SL}_n(A_s)$ and $\tau _2\in \mathrm{SL}_n(A_t)$ such that $\sigma \varepsilon = \tau _1\sigma \tau _2$.

Proof

Let $\varepsilon = \varepsilon _1\varepsilon _2$, where $\varepsilon _1\in \mathrm{SL}_n(A_s)$ is chosen such that $\varepsilon _1 = I_n\;\text {mod}\;(t^{N})$ for sufficiently large N and $\varepsilon _2\in \mathrm{SL}_n(A_t)$. So, we have $\sigma \varepsilon = \sigma \varepsilon _1\varepsilon _2 = \sigma \varepsilon _1\sigma ^{-1}\sigma \varepsilon _2$. Now, since $\varepsilon _1 = I_n\;\text {mod}\;(t^{N})$ for sufficiently large N, $\sigma \varepsilon _1\sigma ^{-1}\in \mathrm{SL}_n(A_s)$. Now by taking $\tau _1 = \sigma \varepsilon _1\sigma ^{-1}$ and $\tau _2 = \varepsilon _2$, we have $\sigma \varepsilon = \tau _1\sigma \tau _2$.

3 The Group $\Gamma (A)$

In this Section, we define the group $\Gamma (A)$ which is an algebraic analogue of the group $H^1(X,\mathbb {Z})$.

Definition 15.4

Let A be a ring. We say a matrix $\alpha \in \mathrm{SL}_2(A)$ can be connected to the identity matrix $I_2$ if there exists a matrix $\beta (T) \in \mathrm{SL}_2 (A[T])$ such that $\beta (0) = I_2$ and $\beta (1) = \alpha$.

Definition 15.5

We say that two unimodular rows (a, b),   (c, d) over A are equivalent, written as $(a, b)\sim (c, d)$, if one (and hence both) of the following equivalent conditions hold.

• 1. There exists $(f_{11} (T), f_{12}(T)) \in \mathrm{Um}_2 (A[T])$ such that $(f_{11} (0), f_{12}(0)) = (a, b)$ and $(f_{11} (1), f_{12}(1)) = (c, d)$.

• 2. There exists a matrix $\alpha \in \mathrm{SL}_2 (A)$ which is connected to the identity matrix (that is, there exists a matrix $\beta (T) \in \mathrm{SL}_2 (A[T])$ such that $\beta (0) = I_2$ and $\beta (1) = \alpha$) such that $\alpha \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} c \\ d \end{pmatrix}$.

The fact that $\sim$ is an equivalence relation will be established later. We first show that these two conditions are equivalent.

$\mathbf{(2)}\Longrightarrow \mathbf{(1)}$.

Suppose $\beta (T) = \begin{pmatrix} g_{11}(T) &{} g_{12}(T) \\ g_{21}(T) &{} g_{22}(T) \end{pmatrix}$ such that $\beta (0) = I_2$ and $\beta (1) = \alpha$, which means

$$ ag_{11}(1) + bg_{12}(1) = c \;\text {and}\; ag_{21}(1)+ bg_{22}(1)= d. $$

Let

$$\begin{aligned} \begin{pmatrix}f_{11}(T)\\ f_{12}(T)\end{pmatrix} = \beta (T)\begin{pmatrix}a\\ b\end{pmatrix} = \begin{pmatrix}ag_{11}(T)+bg_{12}(T)\\ ag_{21}(T)+bg_{22}(T)\end{pmatrix}. \end{aligned}$$

(15.4)

Thus, it is clear that

$$ (f_{11} (0), f_{12}(0)) = (a, b)\;\text {and}\;(f_{11}(1), f_{12}(1)) = (c, d). $$

Since (a, b) is unimodular, we have $(a', b') \in A^2$ such that $ab'-ba'=1$. Then

$$ f_{11} (T)f_{22} (T)- f_{12}(T)f_{21} (T) = 1, $$

where $(f_{21} (T), f_{22}(T)) = (a'g_{11}(T)+b'g_{12}(T),$ $a'g_{21}(T)+b'g_{22}(T))$. Thus

$$ (f_{11} (T), f_{12}(T)) \in \mathrm{Um}_2 (A[T]). $$

Therefore, definition (2) implies definition (1).

$\mathbf{(1)}\Longrightarrow \mathbf{(2)}$.

Since $(f_{11}(T),f_{12}(T))\in \mathrm{Um}_2(A[T])$, there exists $(f_{21} (T), f_{22}(T)) \in (A[T])^2$ such that

$$ f_{11} (T)f_{22} (T)- f_{12}(T)f_{21} (T) = 1. $$

Thus $af_{22} (0)- bf_{21} (0) = 1$.

Let $\beta (T) = \begin{pmatrix} f_{11}(T) &{} f_{21}(T) \\ f_{12}(T) &{} f_{22}(T) \end{pmatrix}\begin{pmatrix} f_{22}(0) &{} -f_{21}(0) \\ -b &{} a \end{pmatrix}$. Then $\beta (0) = I_2$ and $\beta (1)\begin{pmatrix} a \\ b \end{pmatrix}$ $= \begin{pmatrix} c \\ d \end{pmatrix}$. For $\alpha = \beta (1)$, the definition (2) follows.

We now turn to proof that $\sim$ is an equivalence relation.

Reflexivity: To show $(a,b)\sim (a,b)$, we use (1) of Definition 15.5 and simply take $(f_{11}(T), f_{12}(T)) = (a, b)$.

Symmetry: Suppose $(a, b)\sim (c, d)$. By (2) of Definition 15.5, there exists a matrix $\alpha \in \mathrm{SL}_2 (A)$ which is connected to the identity matrix such that $\alpha \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} c \\ d \end{pmatrix}$. Since $\alpha ^{-1}$ is also connected to $I_2$ and $\alpha ^{-1} \begin{pmatrix} c \\ d \end{pmatrix} = \begin{pmatrix} a \\ b \end{pmatrix}$, we get $(c, d)\sim (a, b)$.

Transitivity: Suppose $(a, b)\sim (c, d)$ and $(c, d)\sim (e, f)$. Then we have matrices $\alpha , \beta \in \mathrm{SL}_2 (A)$ which are connected to the identity matrix such that $\alpha \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} c \\ d \end{pmatrix}$ and $\beta \begin{pmatrix} c\\ d \end{pmatrix} = \begin{pmatrix} e \\ f \end{pmatrix}$. Therefore $\beta \alpha \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} e \\ f \end{pmatrix}$.

Since $\alpha$ and $\beta$ are connected to the identity matrix, there exist matrices $\gamma (T), \delta (T) \in \mathrm{SL}_2 (A[T])$ such that $\gamma (0) = I_2 = \delta (0)$ and $\gamma (1) = \alpha ,\; \delta (1) = \beta$. Take $\theta (T) = \delta (T)\gamma (T)$. Thus $\theta (0) = I_2$ and $\theta (1) = \beta \alpha$, that is, $\beta \alpha$ is connected to the identity matrix. Hence $(a, b)\sim (e, f)$.

Note that a unimodular row will always be denoted by parenthesis and its equivalence class by $[\;,\;]$. Thus the equivalence class of (a, b) is [a, b].

Definition 15.6

Let $\Gamma (A)$ be the set of all equivalence classes of unimodular rows given by the equivalence relation $\sim$ as above. Define a product $*$ in $\Gamma (A)$ as follows.

Let $(a, b),~ (c, d) \in \mathrm{Um}_2 (A)$. Complete these to $\mathrm{SL}_2(A)$ matrices $\sigma = \begin{pmatrix} a &{} e \\ b &{} f \end{pmatrix}$ and $\tau = \begin{pmatrix} c &{} g \\ d &{} h \end{pmatrix}$. We define product of two elements $[a,b], [c,d]\in \Gamma (A)$ as follows:

$$ [a, b] * [c, d] = [\mathrm{first}\;\mathrm{column}\;\mathrm{of}~ \sigma \tau ] = [ac+de, bc+df]. $$

Claim. $*$ does not depend on the choice of completions.

Let $\sigma ' = \begin{pmatrix} a &{} e' \\ b &{} f' \end{pmatrix}$ and $\tau ' = \begin{pmatrix} c &{} g' \\ d &{} h' \end{pmatrix} \in \mathrm{SL}_2 (A)$ be another completion of (a, b) and (c, d), respectively. Since columns of $\sigma$ and $\sigma '$ form bases of $A^2$, columns of $\sigma '$ can be written as linear combination of columns of $\sigma$. Since $\sigma$ and $\sigma '$ in $\mathrm{SL}_2 (A)$, $\sigma ' = \sigma \begin{pmatrix}1&{}\lambda \\ 0&{}1\end{pmatrix}$ for some $\lambda \in A$. Similarly $\tau ' =\tau \begin{pmatrix}1&{}\mu \\ 0&{}1\end{pmatrix}$ for some $\mu \in A$. Therefore

$$ \sigma '\tau ' = \sigma \begin{pmatrix}1&{}\lambda \\ 0&{}1\end{pmatrix}\tau \begin{pmatrix}1&{}\mu \\ 0&{}1\end{pmatrix}. $$

Consider the matrix

$$ \beta (T) = \sigma \begin{pmatrix}1&{}\lambda T\\ 0&{}1\end{pmatrix}\tau \begin{pmatrix}1&{}\mu T\\ 0&{}1\end{pmatrix}\tau ^{-1}\sigma ^{-1} \in \mathrm{SL}_2 (A[T]). $$

Thus

$$ \beta (0) = \sigma \begin{pmatrix}1&{}0\\ 0&{}1\end{pmatrix}\tau \begin{pmatrix}1&{}0\\ 0&{}1\end{pmatrix}\tau ^{-1}\sigma ^{-1} = I_2, \text { and } $$

$$ \beta (1)\sigma \tau = \sigma \begin{pmatrix}1&{}\lambda \\ 0&{}1\end{pmatrix}\tau \begin{pmatrix}1&{}\mu \\ 0&{}1\end{pmatrix} \tau ^{-1}\sigma ^{-1}\sigma \tau = \sigma '\tau '. $$

Therefore

$$ \beta (1)\sigma \tau \begin{pmatrix}1\\ 0\end{pmatrix} = \sigma '\tau ' \begin{pmatrix}1\\ 0\end{pmatrix}. $$

Hence $[(ac+de, bc+df)] = [(ac+de', bc+df')]$. So $*$ does not depend on the choice of completions.

Claim. $*$ is a well-defined operation on $\Gamma (A)$, that is, we have to show that if $(a, b)\sim (a', b')$ and $(c, d)\sim (c', d')$, then

$$\begin{aligned}{}[a,b]*[c,d] = [a',b']*[c',d']. \end{aligned}$$

(15.5)

Since $(a, b)\sim (a', b')$ and $(c, d)\sim (c', d')$, there exist $(f_{11}(T), f_{12}(T))$ and $(g_{11}(T),$ $g_{12}(T))$ in $\mathrm{Um}_2 (A[T])$ such that

$$ (f_{11}(0),f_{12}(0)) = (a, b),\;(f_{11}(1), f_{12}(1)) = (a', b'), $$

$$ (g_{11}(0), g_{12}(0)) = (c, d),\;(g_{11}(1), g_{12}(1)) = (c', d'). $$

Again there exist $f_{21}(T)$, $f_{22}(T)$, $g_{21}(T)$, $g_{22}(T)$ in A[T] such that

$$ f_{11}(T) f_{21}(T) - f_{12}(T)f_{22}(T) = 1\;\text {and}\; g_{11}(T) g_{21}(T) - g_{12}(T)g_{22}(T) = 1. $$

Consider $\sigma (T) = \begin{pmatrix} f_{11}(T) &{} f_{22}(T) \\ f_{12}(T) &{} f_{21}(T) \end{pmatrix}$ and $\tau (T) = \begin{pmatrix} g_{11}(T) &{} g_{22}(T) \\ g_{12}(T) &{} g_{21}(T) \end{pmatrix}$ in $\mathrm{SL}_2(A[T])$. Thus the first column of the product $\sigma (T)\tau (T)$ is unimodular, that is,

$$\begin{aligned} (f_{11}(T)g_{11}(T) + f_{22}(T)g_{12}(T), f_{12}(T)g_{11}(T) + f_{21}(T)g_{12}(T)) \in \mathrm{Um}_2 (A[T]). \end{aligned}$$

(15.6)

Setting $T = 0$ and $T = 1$ in (15.6), we get (15.5). Hence the product ‘$*$’ is well defined.

Since matrix multiplication is associative, the product $*$ is associative. Since $[a, b] * [1, 0] = [a, b]$ for every $(a, b) \in \mathrm{Um}_2 (A)$, we see that [1, 0] is the identity element. Let $(a, b) \in \mathrm{Um}_2 (A)$ and $\sigma = \begin{pmatrix} a &{} e \\ b &{} f \end{pmatrix}\in \mathrm{SL}_2(A)$. Then $\sigma ^{-1} = \begin{pmatrix} f &{} -e \\ -b &{} a \end{pmatrix}$ and $[a, b] * [f, -b] = [1, 0]$. So $[f,-b]$ is the inverse of [a, b] in $(\Gamma (A),*)$. Hence $(\Gamma (A),*)$ forms a group.

Now, let A be an integral domain and $a, b \in A$ be such that $aA + bA = A$. Define the maps

$$\varphi : \Gamma (A) \longrightarrow \Gamma (A_a) \oplus \Gamma (A_b)$$

given by $\varphi (\lambda ) = (\lambda , \lambda )$ and

$$ \psi : \Gamma (A_a) \oplus \Gamma (A_b) \longrightarrow \Gamma (A_{ab}) $$

given by $\psi (\lambda , \mu ) = \lambda - \mu$. We would like these maps to be homomorphisms but since $\Gamma (A)$ is not known to be abelian, $\psi$ may not be a homomorphism.

Claim. $\Gamma (A) \overset{\varphi }{\longrightarrow }\Gamma (A_a) \oplus \Gamma (A_b) \overset{\psi }{\longrightarrow }\Gamma (A_{ab})$ is an exact sequence of groups.

To prove the claim, suppose we have elements $\lambda \in \Gamma (A_a)$ and $\mu \in \Gamma (A_b)$ which are equal in $\Gamma (A_{ab})$, that is, there is an element $\alpha (T)\in \mathrm{SL}_2(A_{ab}[T])$ such that $\alpha (0) = I_2$, and $\lambda = \alpha (1)\mu$. We split $\alpha (T)$ (by Lemma 15.1) as $\alpha _1(T)\alpha _2(T)$, where $\alpha _1(T)\in \mathrm{SL}_2(A_a[T])$ with $\alpha _1(0) = I_2$ and $\alpha _2(T)\in \mathrm{SL}_2(A_b[T])$ with $\alpha _2(0) = I_2$. Therefore $\alpha _1(1)^{-1}\lambda = \alpha _2(1)\mu$ and these elements patch to yield an element of $\alpha \in \Gamma (A)$. So $\varphi (\alpha ) = (\alpha , \alpha ) = (\lambda , \mu )$. Hence $\text {ker}(\psi ) \subseteq \text {Im}(\phi )$.

By the definition of $\varphi$ and $\psi$, it is clear that $\text {Im}(\phi ) \subseteq \text {ker}(\psi )$. Hence the claim.

Another way of formulating this is to say that

is a fiber product diagram.

Remark 15.1

Let N be the set of $\alpha \in \mathrm{SL}_2(A)$ such that there exists $\beta (T)\in \mathrm{SL}_2(A[T])$ with $\beta (0) = I_2$ and $\beta (1) = \alpha$. Then N is the connected component of $I_2$ in $\mathrm{SL}_2(A)$ and $N\supset E_2(A)$. The group $\Gamma (A)$ can also be defined to be the quotient group $\mathrm{SL}_2(A)/N$. The reason we cannot take N to be $E_2(A)$ is that $E_2(A)$ is not in general normal in $\mathrm{SL}_2(A)$ and therefore it is necessary to consider a larger group N containing $E_2(A)$.

4 On the Group $\pi _1 (\mathrm{SL}_{2}(A))$

In this section, we define the group $\pi _1 (\mathrm{SL}_{2}(A))$ and give a connecting homomorphism between $\pi _1 (\mathrm{SL}_{2}(A))$ and $\Gamma (A)$. Throughout this section, we assume A as an integral domain.

Let L be the set of loops in $\mathrm{SL}_{2}(A)$ starting and ending at the identity matrix $I_2$, that is, $L =\{\alpha (T)\in \mathrm{SL}_{2}(A[T])\mid \alpha (0) = \alpha (1) = I_2\}$. We say that two loops $\alpha (T), \beta (T) \in L$ are equivalent (that is, written as $\alpha (T)\sim _1 \beta (T)$) if they are homotopic, that is, there exists $\gamma (T, S)\in \mathrm{SL}_{2}(A[T, S])$ such that $\gamma (T, 0) = \alpha (T), \gamma (T, 1) = \beta (T)$ and $\gamma (0,S) = \gamma (1, S) = I_2$. We call $\gamma (T, S)$ to be a homotopy between $\alpha (T)$ and $\beta (T)$.

We now show that $\sim _1$ is an equivalence relation.

Reflexivity: To show $\alpha (T) \sim _1\alpha (T)$, we simply take $\gamma (T, S)= \alpha (T) \in \mathrm{SL}_{2}(A[T, S])$. This is obviously the desired homotopy.

Symmetry: Suppose $\gamma (T, S)\in \mathrm{SL}_{2}(A[T, S])$ is the homotopy between $\alpha (T)$ and $\beta (T)$. Then $\gamma (T, 1-S)$ is a homotopy between $\beta (T)$ and $\alpha (T)$.

Transitivity: Let $\alpha (T)\sim _1 \beta (T)$ and $\beta (T)\sim _1 \delta (T)$. Then there exist matrices $\gamma _1(T, S)$, $\gamma _2(T, S)$ in $\mathrm{SL}_{2}(A[T, S])$ such that $\gamma _1(T, 0) = \alpha (T)$, $\gamma _1(T, 1) = \beta (T)$, $\gamma _1(0,S) = \gamma _1(1, S) = I_2$, $\gamma _2(T, 0) = \beta (T)$, $\gamma _2(T, 1) = \delta (T)$ and $\gamma _2(0,S) = \gamma _2(1, S) = I_2$. Take $\gamma _3(T, S) = \gamma _1(T, S)\beta (T)^{-1}\gamma _2(T, S)$. Hence

$$\begin{aligned} \gamma _3(T, 0)&= \gamma _1(T, 0)\beta (T)^{-1}\gamma _2(T, 0) = \alpha (T),\\ \gamma _3(T, 1)&= \gamma _1(T, 1)\beta (T)^{-1}\gamma _2(T, 1)= \delta (T), \text { and} \\ \gamma _3(0,S)&= \gamma _3(1, S) = I_2 \ (\text {since } \beta (0)^{-1} = \beta (1)^{-1} = I_2). \end{aligned}$$

Thus $\alpha (T)\sim _1 \delta (T)$.

Definition 15.7

For a domain A, $\pi _1 (\mathrm{SL}_{2}(A))$ is the set of all equivalence classes of loops based on $I_2$. For $\alpha (T)\in \mathrm{SL}_2(A[T])$ with $\alpha (0) = \alpha (1) = I_2$, we denote its equivalence class in $\pi _1 (\mathrm{SL}_{2}(A))$ by $[\alpha (T)]$.

Theorem 15.2

The set $\pi _1 (\mathrm{SL}_{2}(A))$ forms an abelian group under the binary operation ‘$*$’ defined as $[\alpha (T)]*[\beta (T)] = [\alpha (T)\beta (T)]$.

Proof

First we show that the operation ‘$*$’ is well defined. Let $\alpha (T)\sim _1 \beta (T)$ and $\gamma (T)\sim _1 \delta (T)$. Then there exist $\gamma _1(T, S), \gamma _2(T, S)\in \mathrm{SL}_{2}(A[T, S])$ such that $\gamma _1(T, 0) = \alpha (T)$, $\gamma _1(T, 1) = \beta (T)$, $\gamma _1(0,S) = \gamma _1(1, S) = I_2$; $\gamma _2(T, 0) = \gamma (T), \gamma _2(T, 1) = \delta (T)$ and $\gamma _2(0,S) = \gamma _2(1, S) = I_2$. Take $\gamma _3(T, S) = \gamma _1(T, S)\gamma _2(T, S)$, we have $\gamma _3(T, 0) = \alpha (T)\gamma (T), \gamma _3(T, 1) = \beta (T)\delta (T)$ and $\gamma _3(0,S) = \gamma _3(1, S) = I_2$. Hence $\alpha (T)\gamma (T) \sim _1 \beta (T)\delta (T)$.

Since matrix multiplication is associative, ‘$*$’ is also associative. Therefore $\pi _1 (\mathrm{SL}_{2}(A))$ is a group with $[I_2]$ as the identity element and $[\alpha (T)^{-1}]$ is the inverse of the element $[\alpha (T)] \in \pi _1 (\mathrm{SL}_{2}(A))$.

Let $\alpha (T), \beta (T) \in L$. Then we will show that $\alpha (T)\sim _1 \beta (T)\alpha (T)\beta (T)^{-1}$. Consider $\gamma (T, S)=\beta (TS)\alpha (T)\beta (TS)^{-1} \in \mathrm{SL}_{2}(A[T, S])$. Then,

• 1. $\gamma (T,0)= \alpha (T),~ \gamma (T, 1)=\beta (T)\alpha (T)\beta (T)^{-1}$,

• 2. $\gamma (0,S) = \gamma (1, S) = I_2$.

Therefore $\alpha (T)\sim _1 \beta (T)\alpha (T)\beta (T)^{-1}$ which means $\alpha (T)\beta (T)\sim _1 \beta (T)\alpha (T)$. This implies that $[\alpha (T)]*[\beta (T)] = [\alpha (T)\beta (T)] = [\beta (T)\alpha (T)] = [\beta (T)]*[\alpha (T)]$. Hence $(\pi _1 (\mathrm{SL}_{2}(A)),*)$ is an abelian group.   $\square$

Let $a, b \in A$ be such that $aA + bA = A$. Define the maps

$$ \varphi _1 : \pi _1 (\mathrm{SL}_{2}(A)) \longrightarrow \pi _1 (\mathrm{SL}_{2}(A_a)) \oplus \pi _1 (\mathrm{SL}_{2}(A_b)), \text { and} $$

$$ \psi _1 : \pi _1 (\mathrm{SL}_{2}(A_a)) \oplus \pi _1 (\mathrm{SL}_{2}(A_b)) \longrightarrow \pi _1 (\mathrm{SL}_{2}(A_{ab})) $$

by $\varphi _1 (\lambda ) = (\lambda , \lambda )\;\text {and}\;\psi _1 (\lambda , \mu ) = \lambda \mu ^{-1}$, respectively. As in the case of $\Gamma (A)$, it is easy to show using Quillen’s splitting that we have an exact sequence of groups

$$ \pi _1 (\mathrm{SL}_{2}(A)) \overset{\varphi _1}{\longrightarrow }\pi _1 (\mathrm{SL}_{2}(A_a)) \oplus \pi _1 (\mathrm{SL}_{2}(A_b)) \overset{\psi _1}{\longrightarrow }\pi _1 (\mathrm{SL}_{2}(A_{ab})). $$

Definition 15.8

(The connecting map ${\Gamma }:\pi _{1}(\mathrm{SL}_2(A_{ab}))\rightarrow \Gamma (A)$) Let $\alpha (T)\in \pi _1(\mathrm{SL}_2(A_{ab}))$, that is, $\alpha (T)\in \mathrm{SL}_2(A_{ab}[T])$ such that $\alpha (0) = \alpha (1) = I_2$. Let $\alpha (T) = \alpha _1(T)^{-1}\alpha _2(T)$ be a Quillen splitting, where $\alpha _1(T)\in \mathrm{SL}_2(A_a[T])$ with $\alpha _1(0) = I_2$ and $\alpha _2(T)\in \mathrm{SL}_2(A_b[T])$ with $\alpha _2(0) = I_2$. Then $\alpha (1) = I_2 = \alpha _1(1)^{-1}\alpha _2(1)$. Hence $\alpha _1(1) = \alpha _2(1)$ and $\alpha _1(1)$ and $\alpha _2(1)$ patch up to yield an element $\gamma \in \mathrm{SL}_2(A)$. We define $\Gamma ([\alpha (T)]) = [\mathrm{first}\;\mathrm{column}\;\mathrm{of}~ \gamma ]$ in $\Gamma (A)$. We will also write it as $\Gamma ([\alpha (T)]) = \alpha _2(1) \begin{pmatrix} 1\\ 0 \end{pmatrix}$.

Theorem 15.3

• 1. The above association does not depend on the Quillen splitting of $\alpha$.

• 2. $\Gamma$ is a well-defined map.

• 3. $\Gamma$ is a group homomorphism.

• 4. The sequence of groups

  $$\begin{aligned} \pi _1(\mathrm{SL}_2(A_{ab}))\overset{\Gamma }{\rightarrow } \Gamma (A)\overset{\phi }{\rightarrow }\Gamma (A_a)\oplus \Gamma (A_b) \end{aligned}$$

  (15.7)

  is exact.

Proof

(1) Suppose we are given two Quillen splittings of $\alpha (T)$ as follows:

$$\begin{aligned} \alpha (T) = \alpha _1(T)^{-1}\alpha _2(T);\;\alpha (T) = \beta _1(T)^{-1}\beta _2(T), \end{aligned}$$

(15.8)

where $\alpha _1(T), \beta _1(T)\in \mathrm{SL}_2(A_a[T])$ with $\alpha _1(0) = \beta _1(0) = I_2$ and $\alpha _2(T), \beta _2(T)\in \mathrm{SL}_2(A_b[T])$ with $\alpha _2(0) = \beta _2(0) = I_2$. Then $\alpha _1(T)^{-1}\alpha _2(T) = \beta _1(T)^{-1}\beta _2(T)$ or we have

$$\begin{aligned} \beta _1(T)\alpha _1(T)^{-1} = \beta _2(T)\alpha _2(T)^{-1} \end{aligned}$$

(15.9)

and these patch up to yield $\delta (T)\in \mathrm{SL}_2(A[T])$ such that $\delta (0) = I_2$.

An easy computation using (15.9) yields that multiplication by $\delta (1)$ sends the unimodular row associated to the first Quillen splitting to the unimodular row given by the second Quillen splitting. It now follows by definition that the element $[\Gamma (\alpha )]$ in $\Gamma (A)$ does not depend upon the choice of Quillen splitting.

(2) Now we have to show that $\Gamma$ is well defined, that is, the homotopic loops in $\mathrm{SL}_2(A_{ab})$ go to the same element of $\Gamma (A)$.

Let $\alpha (T)$, $\beta (T)$ be loops in $\mathrm{SL}_2(A_{ab}[T])$ with $\alpha (0) = \beta (0) = \alpha (1) = \beta (1) = I_2$, which are homotopic as loops. That is, there exists $\gamma (T,S)\in \mathrm{SL}_2(A_{ab}[T,S])$ such that $\gamma (T,0) = \alpha (T)$, $\gamma (T,1) = \beta (T)$ and $\gamma (0,S) = I_2 = \gamma (1,S)$. Since $\gamma (0,S) = I_2$, we can write $\gamma (T,S) = \gamma _1(T,S)^{-1}\gamma _2(T,S)$, where $\gamma _1(T,S)\in \mathrm{SL}_2(A_{a}[T,S])$ with $\gamma _1(0,S) = I_2$ and $\gamma _2(T,S)\in \mathrm{SL}_2(A_{b}[T,S])$ with $\gamma _2(0,S) = I_2$.

Further,

$$\alpha (T) = \gamma (T,0) = \gamma _1(T,0)^{-1}\gamma _2(T,0), \text { and}$$

$$\beta (T) = \gamma (T,1) = \gamma _1(T,1)^{-1}\gamma _2(T,1)$$

are Quillen splittings.

Consider the matrix $\gamma '\in \mathrm{SL}_2(A)$ obtained by patching $\gamma _1(1,0)$ and $\gamma _2(1,0)$, the matrix $\gamma ''\in \mathrm{SL}_2(A)$ obtained by patching $\gamma _1(1,1)$ and $\gamma _2(1,1)$ and $\widetilde{\gamma }(S)$ obtained by patching $\gamma _1(1,S)$ and $\gamma _2(1,S)$. Then the first column of $\widetilde{\gamma }(S)$ is a unimodular row in A[S] which at $S = 0$ is the first column of $\gamma '$ and at $S = 1$ is the first column of $\gamma ''$. Thus $\Gamma$ is well defined.

(3) Let $\alpha (T), \beta (T)\in \mathrm{SL}_2(A_{ab}[T])$ with $\alpha (0) = \beta (0) = I_2$ and $\alpha (1) = \beta (1) = I_2$. Suppose $\alpha (T) = \alpha _1(T)^{-1}\alpha _2(T)$ and $\beta (T) = \beta _1(T)^{-1}\beta _2(T)$ be Quillen splittings of $\alpha (T)$ and $\beta (T)$, respectively. Then $\Gamma ([\alpha (T)]) = \alpha _2(1)\begin{pmatrix}1\\ 0\end{pmatrix}$ and $\Gamma ([\beta (T)]) = \beta _2(1)\begin{pmatrix}1\\ 0\end{pmatrix}$. Thus

$$ \Gamma ([\alpha (T)])*\Gamma ([\beta (T)])= (\alpha _2(1)\begin{pmatrix}1\\ 0\end{pmatrix})*(\beta _2(1) \begin{pmatrix}1\\ 0\end{pmatrix})= \alpha _2(1)\beta _2(1)\begin{pmatrix}1\\ 0\end{pmatrix}, $$

by the definition of $*$ in $\Gamma (A)$. On the other hand, we have

$$\begin{aligned} \alpha (T)\beta (T)= & {} \alpha _1(T)^{-1}\alpha _2(T)\beta _1(T)^{-1}\beta _2(T)\\= & {} \alpha _1(T)^{-1}\alpha _2(T)\beta _1(T)^{-1}\alpha _2(T)^{-1}\alpha _2(T)\beta _2(T).\nonumber \end{aligned}$$

(15.10)

Since $\beta _1(T)$ and hence $\beta _1(T)^{-1}$ can be chosen (see Lemma 15.1) such that $\beta _1(T) \equiv I_2\;\text {(mod}\;b^N\text {)}$ for sufficiently large N, as in Lemma 15.2, we may assume that

$$ \alpha _2(T)\beta _1(T)^{-1}\alpha _2(T)^{-1} \in \mathrm{SL}_2(A_{a}[T]). $$

Therefore the Quillen splitting of $\alpha (T)\beta (T)$ is $\mu (T)\alpha _2(T)\beta _2(T)$, where $\mu (T)$ is a matrix in $\mathrm{SL}_2(A_a[T])$, $\mu (0) = I_2$ and $\alpha _2(T)\beta _2(T)\in \mathrm{SL}_2(A_b[T])$ with $\alpha _2(0)\beta _2(0) = I_2$. Therefore,

$$ \Gamma ([\alpha (T)\beta (T)]) = \alpha _2(1)\beta _2(1)\begin{pmatrix}1\\ 0\end{pmatrix} = \Gamma ([\alpha (T)])*\Gamma ([\beta (T)]). $$

Hence $\Gamma$ is a group homomorphism.

(4) By the definition of $\Gamma$, it is clear that $\text {Im}(\Gamma ) \subseteq \text {ker}(\phi )$. Conversely, let $[(e,f)]\in \text {ker}(\phi )$ that is, $[(e,f)] = [(1, 0)]$ in $\Gamma (A_a)$ and $\Gamma (A_b)$. This implies that we can get matrices $\alpha _1(T)\in \mathrm{SL}_2(A_a[T])$ and $\alpha _2(T) \in \mathrm{SL}_2(A_b[T])$ with $\alpha _1(0) = I_2 = \alpha _2(0)$, $\alpha _1(1)\begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} e\\ f \end{pmatrix}$ and $\alpha _2(1)\begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} e\\ f \end{pmatrix}$.

We have $\alpha _2(1)^{-1}\alpha _1(1)\begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} 1\\ 0 \end{pmatrix}$. This implies that $\alpha _2(1)^{-1}\alpha _1(1) = \begin{pmatrix} 1&{}\mu \\ 0&{}1 \end{pmatrix},$ where $\mu \in A_{ab}$. Further, we have $\begin{pmatrix} 1&{}\mu \\ 0&{}1 \end{pmatrix} = \begin{pmatrix} 1&{}\mu _2\\ 0&{}1 \end{pmatrix}\begin{pmatrix} 1&{}-\mu _1\\ 0&{}1 \end{pmatrix},$ where $\mu _1\in A_a$ and $\mu _2\in A_b$. Thus

$$ \alpha _2(1)\begin{pmatrix} 1&{}\mu _2\\ 0&{}1 \end{pmatrix} = \alpha _1(1)\begin{pmatrix} 1&{}\mu _1\\ 0&{}1 \end{pmatrix}. $$

Let $\beta _1(T) = \alpha _1(T)\begin{pmatrix} 1&{}\mu _1T\\ 0&{}1 \end{pmatrix}$ and $\beta _2(T) = \alpha _2(T)\begin{pmatrix} 1&{}\mu _2T\\ 0&{}1 \end{pmatrix}$. Then

$$\Gamma ([\beta _1(T)^{-1}\beta _2(T)]) = \begin{pmatrix} e\\ f \end{pmatrix}. $$

Hence $\text {Im}(\Gamma ) \supseteq \text {ker}(\phi )$. Therefore we have an exact sequence $\pi _1 (\mathrm{SL}_{2}(A)) \overset{\varphi _1}{\longrightarrow }\pi _1 (\mathrm{SL}_{2}(A_a)) \oplus \pi _1 (\mathrm{SL}_{2}(A_b)) \overset{\psi _1}{\longrightarrow }\pi _1(\mathrm{SL}_2(A_{ab}))\overset{\Gamma }{\rightarrow } \Gamma (A)\overset{\phi }{\rightarrow }\Gamma (A_a)\oplus \Gamma (A_b) \overset{\psi }{\longrightarrow }\Gamma (A_{ab})$.                   (**)   $\square$

5 On Cocycles Associated to Alternating Matrices

In this section, we associate cocycles to alternating forms on projective modules.

Let A be a domain and P be a projective A-module of rank 2. Suppose there exist $f_1,f_2\in A$ such that $f_1A + f_2A = A$ and $P_{f_1}\simeq A_{f_1}^2$, $P_{f_2}\simeq A_{f_2}^2$.

Since $P_{f_1}$ and $P_{f_2}$ are free, there exist bases $\{p_1,p_2\}$ of $P_{f_1}$ and $\{p_1',p_2'\}$ of $P_{f_2}$. Therefore we have two bases $\{p_1,p_2\}$ and $\{p_1',p_2'\}$ of $P_{f_1f_2}$. So we can get a matrix $\sigma \in \mathrm{GL}_2(A_{f_1f_2})$ such that $\sigma \begin{pmatrix} p_1'\\ p_2' \end{pmatrix} = \begin{pmatrix} p_1\\ p_2 \end{pmatrix}$.

Definition 15.9

• 1. The matrix $\sigma$ is called cocycle is associated to the projective module P.

• 2. Two cocycles $\sigma _1$ and $\sigma _2$ are said to be equivalent if there exist $\mu _1\in \mathrm{GL}_2(A_{f_1})$ and $\mu _2\in \mathrm{GL}_2(A_{f_2})$ such that $\sigma _2 = \mu _1\sigma _1\mu _2$. In particular, we say that a cocycle $\sigma$ splits if $\sigma$ is equivalent to identity. It is known that a rank 2 projective module P is free if the cocycle associated to P splits.

Now, instead of considering rank 2 projective A-modules one can consider $4\times 4$ invertible alternating matrices over a ring A, where free modules are replaced by

$$ \psi _1\perp \psi _1 = \begin{pmatrix} 0&{}1&{}0&{}0\\ -1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}-1&{}0 \end{pmatrix}. $$

Definition 15.10

• 1. Let $\alpha$ and $\beta$ be two invertible $4\times 4$ alternating matrices over a domain A. We say that $\alpha$ and $\beta$ are isometric if there exists $\gamma \in \mathrm{GL}_4(A)$ such that $\gamma \alpha \gamma ^t = \beta$.

• 2. Let $\alpha \in \mathrm{GL}_4(A)$ be an alternating matrix. Suppose there exist $\alpha _1\in \mathrm{GL}_4(A_{f_1})$ and $\alpha _2\in \mathrm{GL}_4(A_{f_2})$ such that

  $$\alpha _1\alpha \alpha _1^{t} = \psi _1\perp \psi _1;\;\alpha _2\alpha \alpha _2^{t} = \psi _1\perp \psi _1.$$

  Then $\beta = \alpha _1\alpha _2^{-1}$ satisfies $\beta (\psi _1\perp \psi _1)\beta ^{t} = \psi _1\perp \psi _1$ and we say $\beta$ is the cocycle associated to $\alpha$. Clearly $\beta \in \mathrm{Sp}_4(A_{f_1f_2})$.

Lemma 15.3

Let $\beta$ be the cocycle associated to an invertible alternating matrix $\alpha$ as above. If $\beta$ splits in $\mathrm{Sp}_4(A_{f_1f_2})$, then $\alpha$ and $\psi _1\perp \psi _1$ are isometric.

Proof

Since $\beta$ splits, there exist $\delta _1\in \mathrm{Sp}_4(A_{f_1})$ and $\delta _2\in \mathrm{Sp}_4(A_{f_2})$ such that $\beta = \alpha _1\alpha _2^{-1} = \delta _1^{-1}\delta _2 \Rightarrow \delta _1\alpha _1= \delta _2 \alpha _2$. Suppose $\alpha '_1 = \delta _1\alpha _1$ and $\alpha '_2 = \delta _2\alpha _2$. Then $\alpha _{1}' \alpha (\alpha _{1}')^{t}=\psi _1\perp \psi _1; ~ \alpha _{2}' \alpha (\alpha _{2}')^{t}=\psi _1\perp \psi _1,$ where $\alpha _{1}' \in \mathrm{GL}_4(A_{f_1})$ and $\alpha _{2}' \in \mathrm{GL}_4(A_{f_2})$. Also since $\alpha '_1 = \alpha '_2$, we obtain $\widetilde{\alpha }\in \mathrm{GL}_4(A)$ such that $\widetilde{\alpha }\alpha \widetilde{\alpha }^{t} = \psi _1\perp \psi _1$. Therefore $\alpha$ and $\psi _1\perp \psi _1$ are isometric. Thus $\alpha$ is trivial if the cocycle associated to $\alpha$ splits.   $\square$

Suppose $\alpha ,\beta \in \mathrm{GL}_4(A)$ are alternating and

$$ \alpha _1\alpha \alpha _1^{t} = \psi _1\perp \psi _1;\;\alpha _2\alpha \alpha _2^{t} = \psi _1\perp \psi _1, $$

where $\alpha _1 \in \mathrm{GL}_4(A_{f_1})$ and $\alpha _2 \in \mathrm{GL}_4(A_{f_2})$ and

$$\beta _1\beta \beta _1^{t} = \psi _1\perp \psi _1;\;\beta _2\beta \beta _2^{t} = \psi _1\perp \psi _1,$$

where $\beta _1 \in \mathrm{GL}_4(A_{f_1})$ and $\beta _2 \in \mathrm{GL}_4(A_{f_2})$.

Let $\gamma _1 = \alpha _1\alpha _2^{-1}\in \mathrm{Sp}_4(A_{f_1f_2})$ and $\gamma _2 = \beta _1\beta _2^{-1}\in \mathrm{Sp}_4(A_{f_1f_2})$ be the cocycles associated to $\alpha$ and $\beta$. Suppose there exist $\nu _1\in \mathrm{Sp}_4(A_{f_1})$ and $\nu _2\in \mathrm{Sp}_4(A_{f_2})$ such that $\nu _1\gamma _1\nu _2 = \gamma _2$, then one can check that $\alpha$ and $\beta$ are isometric, that is, there exists $\nu \in \mathrm{GL}_4(A)$ such that $\nu \alpha \nu ^{t} = \beta$ (by using same argument as in the proof of Lemma 15.3). This shows that if the cocyles associated to $\alpha$ and $\beta$ are equivalent, then $\alpha$ and $\beta$ are isometric.

Remark 15.2

There is a one-to-one correspondence between alternating forms on a free module of rank n over a ring A and alternating matrices of order n with entries in A.

Proposition 15.1

Let A be a domain of dimension 2. Suppose $f_1A + f_2A = A$ and P, Q are stably free A-modules of rank 2 such that $P_{f_1}$ and $P_{f_2}$ are free and the associated cocycle is $\sigma \in \mathrm{SL}_2(A_{f_1f_2})$ and $Q_{f_1}$, $Q_{f_2}$ are free and the associated cocycle is $\tau \in \mathrm{SL}_2(A_{f_1f_2})$. Let $Q'$ be the projective A-module associated to the cocycle $\sigma \tau$ and s, t,$t'$ be the corresponding alternating forms on P, Q and $Q'$. Then we have an isometry of alternating forms

$$ (P,s)\perp (Q,t) \simeq (A^2,\psi _1)\perp (Q',t'). $$

Proof

Since $P_{f_1}$ and $P_{f_2}$ are free, we have isomorphisms

$$ P_{f_1}{\mathop {\rightarrow }\limits ^{i_1}} A_{f_1}^2;\;P_{f_2}{\mathop {\rightarrow }\limits ^{i_2}}A_{f_2}^2 $$

such that the cocycle associated to P is $\sigma \in \mathrm{SL}_2(A_{f_1f_2})$. Since $\sigma \in \mathrm{SL}_2(A_{f_1f_2})$, the alternating form $s:P\times P\rightarrow A$ is (using the form $\psi _1$ on $A_{f_2}^2)$ given by

$$ s(p_1,p_2) = \text {det}(i_1(p_1),i_1(p_2)) = \text {det}(i_2(p_1), i_2(p_2)). $$

Similarly we have isomorphisms

$$ Q_{f_1}{\mathop {\rightarrow }\limits ^{j_1}} A_{f_1}^2;\;Q_{f_2}{\mathop {\rightarrow }\limits ^{j_2}} A_{f_2}^2 $$

such that the cocycle associated to Q is $\tau \in \mathrm{SL}_2(A_{f_1f_2})$ and alternating form $t:Q\times Q\rightarrow A$ is given by

$$ t(q_1,q_2) = \text {det}(j_1(q_1),j_1(q_2)) = \text {det}(j_2(q_1), j_2(q_2)). $$

Therefore we get an alternating form $s\perp t$ on $P\oplus Q$. Since $P\oplus Q\simeq A^4$ ([1], Bass Cancellation Theorem), $s\perp t$ yields a matrix $\alpha \in \mathrm{GL}_4(A)$ which is alternating.

Further, the isomorphisms $i_1$ and $j_1$ show that $(\alpha )_{f_1}\simeq \psi _1\perp \psi _2$ and isomorphisms $i_2$ and $j_2$ show that $(\alpha )_{f_2}\simeq \psi _1\perp \psi _1$. It is easy to check that the cocycle associated to $\alpha$ is $\begin{pmatrix} \sigma &{}0\\ 0&{}\tau \end{pmatrix}\in \mathrm{Sp}_4(A_{f_1f_2})$.

Further, there are isomorphisms $Q_{f_1}'{\mathop {\rightarrow }\limits ^{\theta _1}} A_{f_1}^2$ and $Q_{f_2}'{\mathop {\rightarrow }\limits ^{\theta _2}} A_{f_2}^2$ such that the associated cocycle is $\sigma \tau$. The isomorphisms $\theta _1$ and $\theta _2$ induce an alternating form $t':Q'\times Q'\rightarrow A$. Now, since $A^2\oplus Q'\simeq A^4$, we get an alternating form $\beta = (A^2,\psi _1)\perp (Q',t')$ on $A^4$, which in view of the isomorphisms $\theta _1$, $\theta _2$ satisfies the property that $\beta _{f_1}$ and $\beta _{f_2}$ are both isometric to $\psi _1\perp \psi _1$ and the cocycle associated to $\beta$ is $\begin{pmatrix} I_2&{}0\\ 0&{}\sigma \tau \end{pmatrix}$.

Now,

$$ \begin{pmatrix} \sigma ^{-1}&{}0\\ 0&{}\sigma \end{pmatrix}\begin{pmatrix} \sigma &{}0\\ 0&{}\tau \end{pmatrix} = \begin{pmatrix} I_2&{}0\\ 0&{}\sigma \tau \end{pmatrix}. $$

Since $\sigma \in \mathrm{SL}_2(A_{f_1f_2})$ and $\begin{pmatrix} \sigma ^{-1}&{}0\\ 0&{}\sigma \end{pmatrix}\in \mathrm{ESp}_4(A_{f_1f_2})$, (by a lemma of Vaserstein [11], see [2, Lemma 1.2.9 c]), so by a Symplectic version of the Bhatwadekar–Lindel–Rao lemma, whose proof follows exactly the linear case Lemma 15.2, the cocycles $\begin{pmatrix} \sigma &{}0\\ 0&{}\tau \end{pmatrix}$ and $\begin{pmatrix} I_2&{}0\\ 0&{}\sigma \tau \end{pmatrix}$ are equivalent and therefore the alternating forms $(P,s)\perp (Q,t)$ and $(A^2,\psi _1)\perp (Q',t')$ are equivalent. Therefore, we have proved.   $\square$

6 On Some Consequences of the Above Results

We saw in the previous section that if A is a ring and $a,b\in A$ are such that $aA + bA = A$, then we can associate $\sigma \in \mathrm{SL}_2(A_{ab})$ to a projective A-module P of trivial determinant together with a non-singular alternating form $\delta : P\times P\rightarrow A$.

Now, let A be a domain with $\text {dim}\;A = 2$ and S be the set of pairs (P, s), where P is a rank 2 projective module and $s: P\times P\rightarrow A$ is a non-singular alternating form. Then by theorem of Bass [10, Appendix A.7], the set S is an abelian group with the group structure $+$ given by $(P,s) + (Q,t) = (Q',t')$, where $(P,s) \perp (Q,t) \simeq (A^2,\psi _1)\perp (Q',t')$, where $\perp$ denotes the direct sum of alternating forms.

By Proposition 15.1, we have a homomorphism $H\rightarrow S$, where H is the subgroup of $\Gamma (A_{ab})$ corresponding to cocycles corresponding to stably free modules. Since S is abelian group, in particular we have the following:

Corollary 15.1

Let A be a domain with $\text {dim}\;A = 2$. Let $a,b\in A$ be such that $aA + bA = A$. Let $\sigma \in \mathrm{SL}_2(A_{ab})$ and $\tau \in \mathrm{SL}_2(A_{ab})$ be cocycles corresponding to stably free modules. Then $\sigma \tau \sigma ^{-1}\tau ^{-1} = \alpha _1\alpha _2$, where $\alpha _1\in \mathrm{SL}_2(A_a)$ and $\alpha _2\in \mathrm{SL}_2(A_b)$.

Proof

Since S is an abelian group, the image of the element of H corresponding to the cocycle $\sigma \tau \sigma ^{-1}\tau ^{-1}$ in S is the identity element of S that is, the cocycle $\sigma \tau \sigma ^{-1}\tau ^{-1}$ corresponds to a free module of rank 2 over A. Therefore the cocycle $\sigma \tau \sigma ^{-1}\tau ^{-1}$ splits, that is, $\sigma \tau \sigma ^{-1}\tau ^{-1} = \alpha _1\alpha _2$, where $\alpha _1\in \mathrm{SL}_2(A_a)$ and $\alpha _2\in \mathrm{SL}_2(A_b)$ ([9], Theorem 14.4).   $\square$

It would be interesting to see if the restriction that $\text {dim}\;A = 2$ can be removed in Corollary 15.1.

Next we would like to give conditions under which $\Gamma (A)$ is an abelian group. To obtain such condition observe that if $\Gamma (A)$ is an abelian group and $\sigma , \tau \in \mathrm{SL}_2(A)$, then the columns $v = \sigma \tau \begin{pmatrix} 1\\ 0 \end{pmatrix}$ and $w = \tau \sigma \begin{pmatrix} 1\\ 0 \end{pmatrix}$ are equal in $\Gamma (A)$, whereby there exists $\alpha (T)\in \mathrm{SL}_2(A[T])$ such that $\alpha (0) = I_2$ and $\alpha (1)v = w$.

Now, since $\Gamma : \pi _1(\mathrm{SL}_2(A_{ab}))\rightarrow \Gamma (A)$ is a homomorphism and $\pi _1(\mathrm{SL}_2(A_{ab}))$ is an abelian group, its image in $\Gamma (A)$ under $\Gamma$ is likewise abelian and so any pair v, w in the image commute. An element of $\Gamma (A)$ lies in this image if it maps to 0 in $\Gamma (A_a)$ and $\Gamma (A_b)$. This will be the case if we can find elementary completions of the corresponding unimodular row in $A_a$ and $A_b$.

We use these observations to prove the following corollary:

Corollary 15.2

Let A be a Noetherian domain of dimension one. Then $\Gamma (A)$ is an abelian group.

Proof

Let $[v] = (c,d)$, $[w] = (c',d')$. We want to show that [v] and [w] commute. Since elementary matrices can be connected to the identity matrix, we can perform elementary transformations on v and w without changing the class of v and w in $\Gamma (A)$.

We may, therefore, assume that $d' \ne 0$. Let $\mathfrak {m}_1,\mathfrak {m}_2,\dots ,\mathfrak {m}_r$ be the maximal ideals of A containing $d'$. By replacing d by $d + \lambda c$, we may assume that $d\notin \mathfrak {m}_i$ for any $1\le i \le r$, which implies that $(d) + (d') = A$.

By the Chinese reminder theorem, we may choose $\widetilde{c}\in A$ such that $\widetilde{c} = c\;\text {mod}\;(d)$ and $\widetilde{c} = c'\;\text {mod}\;(d')$. Then $\widetilde{c} = c + \mu d$ and $\widetilde{c} = c' + \mu 'd'$. Therefore, $(c,d) {\mathop {\sim }\limits ^{E_2(A)}} (\widetilde{c},d)$ and $(c',d') {\mathop {\sim }\limits ^{E_2(A)}} (\widetilde{c},d')$ (This idea is well known but we have given an argument for the convenience of the reader). Since $(\widetilde{c},d)$ is unimodular, there exist $g, h\in A$ such that $g\widetilde{c} + hd = 1$ and $g', h'\in A$ such that $g'\widetilde{c} + h'd' = 1$.

Let $a = \widetilde{c}$ and $b = (1 - g\widetilde{c})(1 - g'\widetilde{c})$. Then $\widetilde{c}$ is a unit in $A_a$, d and $d'$ are units in $A_b$. Thus, $(\widetilde{c},d)$ and $(\widetilde{c},d')$ can be completed to elementary matrices in $A_a$ and $A_b$. Hence $[v] = 0$ in $\Gamma (A_a)$ and $\Gamma (A_b)$ and $[w] = 0$ in $\Gamma (A_a)$ and $\Gamma (A_b)$. Therefore [v] and [w] which are in $\Gamma (A)$ commute proving the corollary.   $\square$

Corollary 15.2 leads to the following interesting question:

?Question 1

Does Corollary 15.2 hold for rings of dimension bigger than one?

By using Corollary 15.2, we can say that the exact sequence $(**)$ in Sect. 15.4 for a Noetherian domain of dimension one is an algebraic analogue of the Theorem 15.1.

Remark 15.3

Let A be the coordinate ring of a real affine variety $X = \text {Spec}\;A$. Then any element $a\in A$ gives a continuous function $a:X(\mathbb {R})\rightarrow \mathbb {R}$. Therefore a unimodular row $(a_1,a_2)\in A^2$ gives a continuous map $(a_1,a_2):X(\mathbb {R})\rightarrow \mathbb {R}^2-\{(0,0)\}$.

Two unimodular rows give the same element of $\Gamma (A)$ if the corresponding maps $(a_1,a_2):X(\mathbb {R})\rightarrow \mathbb {R}^2-\{(0,0)\}$ are homotopic. Thus the group $\Gamma (A)$ can be considered in a certain sense as the algebraic analogue of the set of homotopy classes of continuous maps from $X\rightarrow \mathbb {R}^2-\{(0,0)\}$ or the homotopy classes of continuous maps X to $S^1$ or the group $H^1(X,\mathbb {Z})$.

Further, if A is the coordinate ring of a real affine variety $X = \text {Spec}\;A$ (as above), then an element of $\pi _1(\mathrm{SL}_2(A))$ gives a continuous function from $X(\mathbb {R})\rightarrow \pi _1(\mathrm{SL}_2(\mathbb {R}))$ and $\pi _1(\mathrm{SL}_2(\mathbb {R})) = \mathbb {Z}$. Thus $\pi _1(\mathrm{SL}_2(A)))$ can be considered $H^0(\text {Spec}(A),\pi _1(\mathrm{SL}_2(A)))$ which is the analogue of the group $H^0(X, \mathbb {Z})$ (the set of continuous maps from X to $\mathbb {Z}$ or the free abelian group on the set of connected component of X).

Now the group homomorphism $\Gamma : \pi _1(\mathrm{SL}_2(A_{ab})) \longrightarrow \Gamma (A)$ shows that the $H^1(\text {Spec}(A),\pi _1(\mathrm{SL}_2(A)))$ is connected to the group $H^1(X,\mathbb {Z})$. So one can ask ‘is the group $H^2(\text {Spec}(A),\pi _1(\mathrm{SL}_2(A)))$ connected to the group $H^2(X,\mathbb {Z})$?’ This was the suggestion of Nori. We elaborate this in the next remark. The cohomology groups are considered in this remark with respect to Zariski topology on $\text {Spec}(A)$.

Remark 15.4

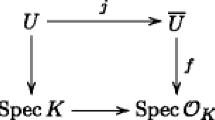
Let A be a domain and $\widetilde{\Gamma }(A) = \{\alpha (T)\in \mathrm{SL}_2(A[T]): \alpha (1) = I_2\}$, We have a homomorphism $\widetilde{\Gamma }(A)\rightarrow \mathrm{SL}_2(A)$ sending $\alpha (T)$ to $\alpha (0)$. A projective A-module P of rank 2 and trivial determinant gives a cocycle $H^1(X,\mathrm{SL}_2)$, where $X = \text {Spec}\;A$. By Quillen’s localization theorem [8], a projective A-module P of rank 2 is free if the 1-cocycle associated to P belonging to $H^1(X,\mathrm{SL}_2)$ can be lifted to $H^1(X,\widetilde{\Gamma })$. Let N(A) be the kernel of the map $\widetilde{\Gamma }(A)$ to $\mathrm{SL}_2(A)$ given above, that is,

$$ 1\rightarrow N(A)\rightarrow \widetilde{\Gamma }(A)\rightarrow \mathrm{SL}_2(A)\rightarrow 1 $$

is exact.

Nori suggested to the first author that one should use the above exact sequence to define a connecting map $H^1(X,\mathrm{SL}_2(A))\rightarrow H^2(X,N/N_0)$, where $N_0(A)$ is the connected component of identity of N(A) and associate to P an obstruction in $H^2(X,N/N_0)$, and show that if dimension of A is 2 and this obstruction vanishes then P is free (Nori also showed that $N(A)/N_0(A)\simeq \pi _1(\mathrm{SL}_2(A))$). Therefore $H^2(X,N(A)/N_0(A))$ is same as $H^2(\text {Spec}(A),\pi _1(\mathrm{SL}_2(A)))$. This was Nori’s original approach to defining a group to evaluate Euler Classes.

We will try to show how Nori’s suggestion motivated our work. We consider the following problem:

?Question 2

Can one associate an obstruction to a matrix in $\mathrm{SL}_2(A)$ whose vanishing implies the matrix is trivial in $\Gamma (A)$?

We know that over a local ring B any matrix belonging to $\mathrm{SL}_2(B)$ is elementary, and therefore can be connected to the identity matrix.

Let

$$ \Gamma '(A) = \{\beta (T)\in \mathrm{SL}_2(A[T]): \beta (0) = I_2\}. $$

We have a map $\Gamma '(A)\rightarrow \mathrm{SL}_2(A)$ given by $\beta \rightarrow \beta (1)$.

A matrix $\alpha \in \mathrm{SL}_2(A)$ can be connected to the identity matrix if $\alpha$ can be lifted to $\Gamma '(A)$ under the above map. Suppose there exist $a, b\in A$ such that $aA + bA = A$, and $\alpha \in \mathrm{SL}_2(A)$ is such that both $(\alpha )_a$ and $(\alpha )_b$ can be connected to the identity matrix, that is, there exist $\beta _1(T)\in \Gamma '(A_a)$ which is a lift of $(\alpha )_a$ and $\beta _2(T)\in \Gamma '(A_b)$ which is a lift of $(\alpha )_b$. Then $\beta _1\beta _2^{-1}\in \pi _1(\mathrm{SL}_2(A_{ab}))$. This leads us to consider the map $\pi _1(\mathrm{SL}_2(A_{ab}))$ to $\Gamma (A)$ discussed in this paper and naturally to the other results of this paper.

Remark 15.5

It would be interesting to know other places where the group $\Gamma (A)$ is used and where it first occurs. We have been able to trace its occurrence to a paper of Krusemeyer [7, Lemma 3.3] who refers to a paper of Karoubi–Villamayor (see [6]).

The exact sequence

$$ 1\rightarrow \pi _1(\mathrm{SL}_2(A))\rightarrow \Gamma (A)\rightarrow \mathrm{SL}_2(A)\rightarrow 1 $$

occurs in [7, Lemma 3.6]. The main idea of this paper is to write down a Mayer–Vietoris sequence associated to the above exact sequence.