Keywords

1 Introduction and Related Work

In the current digital era, protecting sensitive information has become a cumbersome task. Research shows that biometrics are more prominent than the traditional passwords for authentication and authorization. Face recognition is a class of biometrics that maps a person’s facial features mathematically and stores the information as a faceprint. Face Recognition even surpasses other biometric modalities because it is non-intrusive and can identify a distant subject. Face recognition unlike other physiological modalities does not require any special hardware component. Any modern-day camera can be used for face recognition. Extensive research in the domain of face recognition has led to various classical techniques like FisherFace, Elastic Graph Matching, EigenFace etc.

Feature detection and description are one of the most crucial steps for an image processing task. Over the last decade, Scale Invariant Feature Transform(SIFT) which was suggested by Lowe [1], Speed-Up Robust Features(SURF) which was originally proposed by Herbert Bay [2] and Oriented FAST and Rotated BRIEF(ORB) [3] have been widely used for face recognition. Some of the popular works include—adaptation of SIFT Features for Face Recognition under Varying Illumination [4], SURF-Face [5] and ORB-PCA based feature extraction technique for Face Recognition [6]. The algorithms are subjective to the type of problem that has to be handled. SIFT is a robust classical algorithm which intents to produce scale and orientation invariant features [1] with descriptors which will perform well in matching the state of the image processing pipeline [7]. Analogously, SURF is computationally less exorbitant and mathematically less complicated [2, 8]. It is preeminent because of its standout facets like scale and rotation invariance, repeatability, distinctiveness, and robustness [2]. Similarly, ORB is more efficient than SURF because it uses binary descriptor for feature detection [3, 8]. But for the scale and rotation invariance, it is not as much robust as SURF [3, 7].

However, all these feature descriptors need the facial images to be properly aligned and have a decent contrast. Otherwise, very limited number of key points are detected in the image which produces poor results. Recently an alternative to the traditional SIFT descriptor called the Dense SIFT (DSIFT) descriptor was proposed by Wang [9]. The DSIFT descriptor increases the number of keypoints in an image [9, 10] which in turn enhances the performance of the Face Recognition system. Thus, we propose to exploit DSIFT [9], Dense SURF (DSURF) [5] and Dense ORB(DORB) feature descriptors with a novel pipeline constituting of Laplacian of Gaussian (LoG) filter [11, 12] for enhancing an input image, Fisher vector (FV) for image feature patch aggregation and extended nearest neighbor (ENN) classifier [13] for classification, in this paper. To evaluate the performance of the proposed descriptors comparisons were made with each other and also with the traditional descriptors (SIFT [1], SURF [2] and ORB [3] descriptors). To the best of our knowledge, the application of Dense SURF (DSURF) [5] and DORB on Face Recognition and their comparison with the classical techniques has not been explored yet.

The paper is laid out in the following manner: Sect. 2 describes our proposed system. It contains a detailed explanation of various steps involved along with their usage in our pipeline. Section 3 describes the experimental design. It discusses the various datasets used. Section 4 contains experimental results and their graphical visualization. Section 5 contains various conclusions and inferences that were drawn from the paper. We have also discussed the future enhancements.

2 Proposed System

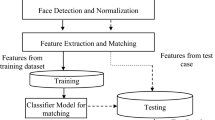
This section discusses the different steps involved in this proposed method including necessary theoretical and mathematical background of each step. The various steps involved in this approach are depicted below. In the suggested approach, LoG filter is applied to enhance an input image [11] i.e. improve contrast and brightness of the image (Fig. 1).

Fig. 1
figure 1

Pipeline for the applied methodology

Full size image

This is depicted in the image below.

figure a

Then the enhanced image is passed to various dense feature descriptors. These descriptors return a feature vector for each of the keypoints in the image. These obtained feature vectors are passed to the Fisher vector which in turn enhances these feature vectors and returns the enhanced feature vectors which are more suitable for classification. Finally, Extended Nearest Neighbour classifier [13] is used to classify the image. The enhanced feature vectors of all the images in the training dataset and their corresponding labels are used to fit the classifier model. The resultant model can then be used to classify any query image.

The implementation involves several tactical changes in the existing SIFT [1], SURF [2] and ORB [3] feature descriptors to produce three novel descriptors: DSIFT [9, 10], DSURF [5] and DORB. The pipeline also includes ENN classifier which is an improved version of the popular K-Nearest Neighbour (KNN) classifier [13]. The results obtained are compared with the classical techniques to state the proficiency of the proposed system.

2.1 Laplacian of Gaussian

2.1.1 Background

Laplacian filter is a second order differential mask [11] which is generally used to find edges in an image [12]. Laplacian operator is isotropic in nature I.e. it is impartial and applies uniformly in all directions in an image. It measures the amount of change in image intensity per change in image position [11].

The Laplacian operator is defined as the dot product of two gradient vector operators [11]

$$ L(x,y) = \left[ {\frac{\partial }{\partial x}\frac{\partial }{\partial y}} \right] \cdot \left[ {\frac{\partial }{\partial x}\frac{\partial }{\partial y}} \right]^{T} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }} $$

The Laplacian operator L(x, y) when applied on an image with intensity values I(x, y), is defined as

$$ {\text{L}}({\text{x}},{\text{y}}) = \frac{{\partial^{2} I}}{{\partial x^{2} }} + \frac{{\partial^{2} I}}{{\partial y^{2} }} $$

A convolution filter can be used to approximate the Laplacian operator. For doing so, a discrete kernel is required that can approximate the second order derivatives used by the Laplacian operator. But, these kernels are highly susceptible to noise [11]. To overcome this, noise within an image needs to be reduced. Smoothing filters reduce the noise in an image and generate a less pixelated image [11].

Generally, the Gaussian smoothing filter is used to reduce the sensitivity of an image to noise. The Gaussian operator is a two-dimensional convolution operator [14] that blurs an image and removes some details and noise in the process. It uses a kernel which has a bell-shaped representation. The Gaussian operator is a circularly symmetric operator [14]. It is given by

$$ {\text{G}}({\text{x}},{\text{y}}) = \frac{1}{{2\uppi \upsigma ^{2} }}{\text{e}}^{{ - \frac{{x^{2} + y^{2} }}{{2\upsigma^{2} }}}} \quad (\upsigma\,represents\,standard\,deviation) $$

The distribution is represented as

figure b

(mean is (0,0) and standard deviation is σ)

The Gaussian operator blurs out any point-like object (in this case a pixel) to a three-dimensional image with certain minimal size and shape. Since the image is represented using discrete pixel values so, before performing convolution a discrete approximation of the Gaussian function must be found. Theoretically, the Gaussian function is always greater than zero, which implies to an infinitely large convolution kernel. But, practically the Gaussian distribution becomes negligible (approximately 0) beyond 3 standard deviations from the mean. So, the convolution kernel can be terminated at this point.

Once an appropriate kernel is obtained, standard convolution techniques can be used to perform Gaussian smoothing. By decomposing the Gaussian kernel into x and y components [14], we can speed up the convolution step. Thus, we can perform the two-dimensional convolution by first convolving in the x-direction using the one-dimensional x component and then convolving in the y-direction using the one-dimensional y component. The Gaussian operator is the only operator which can be divided in such a way [14].

Since convolution is associative in nature, the Gaussian smoothing filter can be convolved with the Laplacian filter [11] and then this LoG filter can be convolved with the image to produce the desired results. LoG function is defined as

$$ \begin{aligned} & LoG(x,y) \\ & \quad = - \frac{1}{{\pi \upsigma ^{4} }}\left[ {1 - \frac{{x^{2} + y^{2} }}{{2\upsigma^{2} }}} \right]{\text{e}}^{{ - \frac{{x^{2} + y^{2} }}{{2\upsigma^{2} }}}} \quad (mean\,is\,(0,0)\,and\,standard\,deviation\,is\,\upsigma) \\ \end{aligned} $$

The LoG function is represented as

figure c

(The x and y axes are marked in standard deviations (σ))

LoG filter has many advantages like: (1) Generally Laplacian and Gaussian kernels are much smaller than the image, so LoG filter requires fewer arithmetic operations. (2) The LoG kernel can be precomputed so, that it can be directly convolved with the image at run-time. Thus, only one convolution is performed per image at run-time.

2.1.2 Usage

Pre-processing images is an integral part of Face Recognition systems. Input images were enhanced by improving the contrast and brightness, in order to optimize the performance of the proposed Face Recognition system.

Knowing the advantages of the LoG filter over the traditional Laplacian and Gaussian filter, LoG filter was chosen for pre-processing the images. LoG filter measures the amount of change of image intensity per change in image position [11]. So, the response of the LoG filter will be zero for all the image patches having a constant pixel intensity. On the other hand, whenever the intensity changes the LoG filter will return a positive response on the darker side and negative response on the lighter side [11]. This is depicted in the image below.

figure d

So, basically LoG filter is used to highlight all the edges present in an image (since intensity changes across an edge). This is depicted in the image in Fig. 2. Gaussian filter removes the additional details and noise from the input image and then the Laplacian filter predicts the edges in the image. Now, when the filtered image is subtracted from the original image then, the edges in the resulting image are much sharper and have higher contrast [11]. So, this enhances the image. This is depicted in the image in Fig. 2.

Fig. 2
figure 2

a Original image, b image obtained after applying LoG filter and c image obtained after subtracting the filtered image from the original image

Full size image

2.2 Feature Descriptors

2.2.1 Dense Sift

SIFT is a feature extraction algorithm which helps in detecting stable feature points in an image. The sole purpose of SIFT algorithm is to obtain the feature descriptors that overcome several computer vision challenges such as rotation invariance, scale invariance and robust to variations in geometric transformations [7]. SIFT extracts features from a given image by detecting interest points in the image [7]. SIFT detector is implemented by the Difference-of-Gaussian function. DoG finds possible interest points that are invariant to scale and rotation [7].

$$ G(x,y,\upsigma) = \frac{1}{{2\pi \upsigma ^{2c} }}\left( {x^{2} + y^{2} } \right)/2\upsigma^{2} $$

DoG is accomplished by the convolving the Gaussian Filter on the image at different scales [7]. DoG image is described as below:

$$ L(x,y,\upsigma) = G(x,y,\upsigma)*l(x,y) $$

Where the term L(x, y,) represents the convolved image. Eventually, the difference between successive Gaussian-blurred images is calculated [7]. The operation of the DoG function is shown below:

$$ D(x,y,\upsigma) = (G(x,y,k\upsigma) - G(x,y,\upsigma))*l(x,y) = L(x,y,k\upsigma) - L(x,y,\upsigma) $$

These key-points reveals detailed information about the location, orientation, and scale. It then computes the local descriptor for the local region around the keypoint. The combination of all these computed descriptors gives the entire feature descriptor for an image [7].

But, SIFT has many limitations. SIFT detector can’t detect enough number of keypoints if an image is ill-illuminated [9]. The classical SIFT detector is generally used on large images to make sure that enough number of interest points are detected [9]. Dense SIFT overcomes these problems by making use of dense pixel grid representation of images and considering the regular image grid points as keypoints [9]. Thus, DSIFT is able to detect a sufficient number of keypoints irrespective of the illumination and size of the image. DSIFT descriptor computes feature descriptors for each of these keypoints producing a dense representation of facial features. These descriptors are finally concatenated to form the feature vector for the face [9].

2.2.2 Dense SURF

SURF was proposed to speed up the computation required by feature detection and extraction [2, 15]. It is made up of a scale and in-plane rotation invariant feature detector and descriptor [2]. The feature detector does the job of detecting keypoints in an image and the is used to describe the features of these detected keypoints by constructing feature vectors.

SURF feature detector uses the determinant of the approximate Hessian matrix as the underlying principle [2]. It calculates the determinant at all the points in the image and detects droplet-like structures wherever the determinant is at maximum [2]. But, these calculations are quite expensive. So, SURF uses integral images to reduce the computation time. For any point x = (x, y) in an image at scale, the Hessian matrix H(x,) is calculated as:

$$ H({\text{x}},\sigma ) = \left[ {\begin{array}{*{20}l} {L_{xx} ({\text{x}},\sigma )} \hfill & {L_{xy} ({\text{x}},\sigma )} \hfill \\ {L_{xy} ({\text{x}},\sigma )} \hfill & {L_{yy} ({\text{x}},\sigma )} \hfill \\ \end{array} } \right] $$

where \( L_{xx} (x,\sigma ), L_{xy} (x,\sigma ), L_{yy} (y,\sigma ) \) are defined as convolutions of Gaussian second order partial derivatives on point x in image I. In order to reduce the computation cost a set of box filters is used by SURF to approximate the Gaussian and represent the lowest scale for computing the droplets (blobs) [2]. These are denoted by \( D_{xx} (x,\sigma ), D_{xy} (x,\sigma )\,and\,D_{yy} (x,\sigma ) \). The result produced is:

$$ \det \left( {H_{appox} } \right) = D_{xx} D_{yy} - \left( {\omega D_{xy} } \right)^{2} $$

where ω is the weight used for conserving energy between Gaussian kernels and approximated Gaussian kernels. The value of ω can be calculated as:

$$ \omega = \frac{{\left| {L_{xy} (1.2)} \right|_{F} \left| {D_{yy} (9)} \right|_{F} }}{{\left| {L_{yy} (1.2)} \right|_{F} \left| {D_{xy} (9)} \right|_{F} }} = 0.912 \approx 0.9 $$

Here, |XF| is Frobenius Norm.

For incorporating scale invariance, like SIFT, SURF also generates a pyramid scale space. But it does this in a unique way. Since SURF makes use of box filters and integral images so it generates the scale space by directly varying the scale of box filters [2].

figure e

SURF feature descriptor is based on the local Haar wavelet responses [2]. It calculates the sum of Haar wavelet responses and uses it to describe the feature of a keypoint. To compute the descriptor a square region centered at the key point is constructed and oriented along the direction given by the orientation selection method [2]. Now the square region is divided into smaller 4 × 4 square sub-regions. Now each sub-region is further split into 5 × 5 squares and Haar wavelet response is calculated for each of these squares. Haar wavelet response in x-direction and y-direction are denoted by dx and dy respectively. To increase robustness towards errors, the responses \( d_{x} \) and \( d_{y} \) are weighted with a Gaussian centered at the keypoint [2].

figure f

Then the sum of wavelet responses \( d_{x} \) and \( d_{y} \) is computed over all the sub-regions. These form the first entries of the feature descriptor of the keypoint [2]. Other entries are also made in order to capture various types of information.

figure g

But, SURF faces problems when an image is small, does not have a proper orientation or is ill-illuminated. DSURF is an enhanced version of SURF. The main problem with the classical SURF detector is that the number of false positives is high [5]. SURF extracts image features by detecting keypoints in the image. But, if the image is not properly oriented or illuminated then very few keypoints are detected in the image leading to very few descriptors [5]. So, DSURF overcomes this limitation by using a dense pixel grid representation for images [5]. It considers the regular image grid points as keypoints and generates descriptors for them. So, DSURF is able to generate a good number of descriptors for every image irrespective of the conditions under which it is captured. Experimental results show that this modified version of SURF is better as it makes keypoint detection invariant to illumination and orientation.

2.2.3 Dense ORB

ORB makes use FAST feature detector and BRIEF descriptor [3]. It adds an orientation component to the well known FAST descriptor by using the Intensity Centroid approach [6] and creates a variant of the classical BRIEF descriptor which is rotation invariant [6].

The Intensity Centroid approach uses a robust measure of corner orientation. The centroid is calculated using the moments of an image patch [6]. The \( (p + q){\text{th}} \) order moment whose intensity function is \( I(x,y) \), can be calculated as:

$$ m_{pq} = \sum\limits_{x,y} {x^{p} y^{q} I(x,y)} $$

Once the moments are calculated then the centroid is given by:

$$ C = \left( {\frac{{m_{10} }}{{m_{00} }},\frac{{m_{01} }}{{m_{00} }}} \right) $$

Now, a vector joining the center and centroid is constructed and the orientation of the patch is calculated by:

$$ \theta = a{ \tan }2\left( {m_{01} ,m_{10} } \right) $$

where atan2 is arctan. This approach incorporates illumination invariance as angle measures are independent of the type of corner [6].

Secondly, ORB includes a rotation invariant component called r-BRIEF [6] which is an improved version of the classical BRIEF descriptor. To achieve rotation invariance, ORB steers the BRIEF in the direction of orientation of key-points [6].

This is achieved in the following way:

Suppose that for any binary feature set constituting of n tests at a point \( \left( {x_{i } ,y_{i} } \right) \) results in a matrix represented as:

$$ S = \left( {\begin{array}{*{20}c} {x_{1} , \ldots ,x_{n} } \\ {y_{1} , \ldots ,y_{n} } \\ \end{array} } \right) $$

Now, by utilizing the patch orientation \( \left( \varTheta \right) \) and corresponding rotation matrix \( \left( {R_{\varTheta } } \right) \) a steered version of the original S can be obtained.

$$ S_{\Theta } = R_{\theta } S $$

Subsequently, the steered BRIEF operator is defined as:

$$ g_{n} (p,\Theta ): = f_{n} (P)|\left( {x_{i} y_{i} } \right) \in S_{\Theta } $$

But, ORB faces problems when an input image is not properly illuminated. ORB uses FAST detector with some modifications to make it invariant to orientation but, it does not handle illumination invariance. So, if an image is ill-illuminated or has low contrast then FAST detects only a few keypoints and is not able to describe the image features properly. DORB overcomes this limitation by using a dense pixel grid representation for images. It increases the number of keypoints in an image by considering regular image grid points as keypoints. So, the number of keypoints detected by DORB is independent of the conditions under which the image is captured. So, now the r-BRIEF descriptor is able to describe every image properly irrespective of its illumination and contrast.

2.3 Fisher Vector

2.3.1 Background

2.3.1.1 Fisher Vector

Patch-aggregation techniques have proved to be effective in recent past, revealing high performance for a variety of computer vision tasks. Fisher Vector (FV) is another patch-aggregation technique which uses Fisher Kerne (FK)l as its underlying principle [16]. FK framework derives a kernel by characterizing an image based on the deviation from a generative data model [17]. The FV is represented vectorially, which is obtained by the calculating the slope of the log-likelihood to the model parameters [13, 17, 18]. FV is a high-dimensional vector formed by aggregating vast set of feature vectors extracted by various feature descriptors (e.g. DSIFT, DSURF, DORB).

2.3.1.2 Fisher Kernel

FK is used because of its potential of being used in learning a model when the training objects have a different underlying graph structure. It is based on the concept of having similar log-likelihood gradients for similarly structured objects in a generative model [17, 18].

Let \( {\text{X}} = \left\{ {{\text{x}}_{\text{n}} ,{\text{t}} = 1,2, \ldots ,{\text{N}}} \right\} \) where xn ∈ χ is a set of D-dimensional local descriptors, like DSIFT, DSURF or DORB descriptors [17]. By the theory of information geometry, a Riemannian manifold MA with a local metric is derived by the Fisher Information Matrix(FIM) Fλ ∈ ℝM × M

$$ F_{\uplambda} = E_{{X \sim u_{\uplambda} }} \left[ {G_{\uplambda}^{X} G_{\uplambda}^{{X^{T} }} } \right] $$

where \( u_{\lambda } \) is the probability density function for the elements in χ where \( \uplambda = \lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{M} \in {\mathbb{R}}^{M} \) which represents a vector with M parameters of \( u_{\lambda } \).

FKl for two samples X and Y is defined as:

$$ {\text{K}}({\text{X}},{\text{Y}}) = G_{\uplambda}^{{X^{T} }} F_{\uplambda}^{ - 1} G_{\uplambda}^{Y} . $$

By the Cholesky decomposition, equation can be written as a dot product:

$$ K_{FK} \left( {X,Y} \right) = \widehat{G}_{\lambda }^{{X^{T} }} \widehat{G}_{\lambda }^{Y} $$

where \( \widehat{\text{G}}_{\lambda }^{X} = L_{\lambda } G_{\lambda }^{X} = L_{\lambda } ?_{\lambda } { \log }\,u_{\lambda } (X) \), \( \widehat{\text{G}}_{\lambda }^{X} \) is known as the Fisher Vector of X. Let us assume that samples are independent, we can write the equation as below:

$$ \widehat{\text{G}}_{\uplambda}^{X} = \sum\limits_{n = 1}^{N} {L_{\uplambda} } \nabla_{\uplambda} { \log }\,u_{\uplambda} (x_{n} ). $$

According to the assumption, FV is a sum of the normalized gradient for each descriptor. The contribution by each xn can be inferred as an embedding of local descriptors xn in a high-dimensional space. Gaussian Mixture Model is selected as \( u_{\lambda } \) [13, 17]. We are denoting T-component GMM by \( \uplambda = \left\{ {w_{t} ,u_{t} ,\varSigma_{t} ,t = 1, \ldots ,T} \right\} \) where \( w_{t} ,u_{t} ,\varSigma_{t} \) are mixture weight, mean vector and covariance matrix of Gaussian t.

\( L_{\lambda } \) is calculated by taking square-root of the inverse of FIM. The normalized gradients can be formulated by performing coordinate-wise normalization of the gradient vectors. Initially, the accumulators are initialized as \( S_{t}^{0} \leftarrow 0,S_{t}^{1} \leftarrow 0,S_{t}^{2} \leftarrow 0 \) for ∀ {t ∈ℝ | 1 ≤ t ≤ T}. For each of the local image descriptors, posterior probability is derived by \( \gamma_{n} (t) = \frac{{\varvec{w}_{\varvec{t}} \varvec{u}_{\varvec{t}} \left( {\varvec{x}_{\varvec{n}} } \right)}}{{\mathop \sum \nolimits_{{\varvec{j} = 1}}^{\varvec{T}} \varvec{w}_{\varvec{j}} \varvec{u}_{\varvec{j}} \left( {\varvec{x}_{\varvec{n}} } \right)}} \), then update the accumulators with the \( S_{t}^{0} ,S_{t}^{1} ,S_{t}^{2} \) with \( \gamma_{n} (t),\gamma_{n} (t)x_{n} \,and\,\gamma_{n} (t)x_{n}^{2} \) respectively [17]. In terms of statistics, these computed normalised gradients can be written in the form of 0th-order, 1st-order and 2nd-order statistics:

$$ \begin{aligned} S_{t}^{0} & = \sum\limits_{n = 1}^{N} {\upgamma_{n} } (t) \\ S_{t}^{1} & = \sum\limits_{n = 1}^{N} {\upgamma_{n} } (t)x_{n} \\ S_{t}^{0} & = \sum\limits_{n = 1}^{N} {\upgamma_{n} } (t)x_{n}^{2} \\ \end{aligned} $$

After the statistics are computed, the signature of the Fisher Vectors for all the t components of the GMM needs to be accounted by the following equations:

$$ \begin{aligned} \widehat{\text{G}}_{{\upalpha_{t} }}^{X} & = \left( {S_{t}^{0} + Nw_{t} } \right)/\sqrt {w_{t} } \\ \widehat{\text{G}}_{{\upmu_{t} }}^{X} & = \left( {S_{t}^{1} +\upmu_{t} S_{t}^{0} } \right)/\sqrt {w_{t} }\upsigma_{t} \\ \widehat{\text{G}}_{{\upsigma_{t} }}^{X} & = \left( {S_{t}^{2} - 2\upmu_{t} S_{t}^{1} + \left( {\upmu_{t}^{2} -\upsigma_{t}^{2} } \right)S_{t}^{0} } \right)/\sqrt {2w_{t} }\upsigma_{t}^{2} \\ \end{aligned} $$

where \( \alpha_{t} \) is the re-parametrization of the following the definition of soft-max formalism. Using the Eq. (19), the components are calculated separately. All the FV components are concatenated to form a single vector representing FV.

To improve the results with various linear classifiers it is a necessity to use normalization techniques. Different normalization techniques have been proposed in past [13, 17]. Some of them are l2-normalization, power normalization. FV depends on some percentage of the image-specific proportion \( (\omega ) \). Accordingly, this can be inferred from the fact that two images having the same objects but different scales have different signatures. l2-normalization is used to eliminate the dependence on ω.

$$ \widehat{\text{G}}_{\uplambda}^{X} = \widehat{\text{G}}_{\uplambda}^{X} /\sqrt {\widehat{\text{G}}_{\uplambda}^{{X^{T} }} \widehat{\text{G}}_{\uplambda}^{{X^{X} }} } $$

Power normalization is applied for all \( {\text{i}} = 1, \ldots ,{\text{T}}\left( {2{\text{D}} + 1} \right) \) of the form:

$$ \left. {\left[ {\widehat{\text{G}}_{\uplambda}^{X} } \right]_{i} - {\text{sign}}\left( {\left[ {\widehat{\text{G}}_{\uplambda}^{X} } \right]_{i} } \right)\sqrt {\left| {\widehat{\text{G}}_{\uplambda}^{X} } \right|_{i} } } \right] $$

In the experiments performed, power coefficient ρ has been set to 1/2. This adjustment is also referred to “signed square rooting” and has been found advantageous for image representations [13, 16].

2.4 Extended Nearest Neighbor Classifier

As the name suggests, this classifier is an extension of the well known KNN classifier. It approximates the optimal Bayes theorem and enhances the performance of KNN and weighted-KNN classifiers [8].

Classifiers are broadly classified into two types namely parametric classifiers and non-parametric classifiers. ENN classifier comes under non-parametric classifier. In non-parametric classifiers, the classification rules are independent of the underlying distribution of input data [8]. Non-parametric classifiers have been used extensively recently.

Talking about the KNN classifiers, they have numerous advantages such as simple implementation, great performance on the data independent of the underlying data distribution.

But they have a lot of shortcomings, like determining the optimal value of k. A straightforward approach to solve this would be to try out different values of k and choose the one which produces optimal results. The second problem is choosing an appropriate distance measure.

KNNs are influenced heavily by the distribution of predefined classes [19]. The outcome, i.e. the classification of the test data is more likely to be decided by the class with higher density. Suppose there are two classes A and B, and class A has a lower variance which means that data points appear to be more concentrated and class B has a distribution which is more spread out. This clearly leads to misclassification of the test data points since the nearest neighbors from class A will be more dominant.

ENNs works independently of the fact that whether the data points of the class are well spread or they have a concentrated distribution. ENN doesn’t only classify the test samples by just finding the nearest neighbors of the predefined classes but also takes into account the test samples as which are their nearest neighbors [8].

Defining the general class wise Ti as the following:

$$ T_{i} = \frac{1}{{n_{i} k}}\sum\limits_{x \in S} {\sum\limits_{r = 1}^{k} {I_{r} \left( {x,A = A_{1} \cup A_{2} } \right)} } $$

where, A1 and A2 denote the samples belonging to the class 1 and class 2. And A is the union of the A1 and A2, k is the number of nearest neighbor. I is the indicator function, sees if both the sample x and it’s rth nearest neighbor are part of the same class, defined as follows:

$$ I_{r} (x,A) = \left\{ {\begin{array}{*{20}c} {1,if\,x \in A{\text{A}}_{\text{i}} \,and\,NN_{r} (x,A)\epsilon A_{i} } \\ {0,\,{\text{otherwise}}} \\ \end{array} } \right. $$

where NNr denotes the rth nearest neighbor of x in A.

The intra-class coherence is defined as follows:

$$ \begin{array}{*{20}c} {\uptheta^{\text{j}} = \sum\limits_{i = 1}^{2} {{\text{T}}_{\text{i}}^{\text{j}} } } \\ {f_{ENN} = \arg \hbox{max} \sum\limits_{t = 1}^{2} {T_{i}^{j} } = \arg \mathop {\hbox{max} }\limits_{j \in 1,2} \theta^{j} } \\ \end{array} $$

ENN.V1

$$ T_{i}^{j} = \frac{1}{{n_{i}^{{\prime }} k}}\sum\limits_{{x \in A_{i} \cup z}} {\sum\limits_{r = 1}^{k} {I_{r} } } \left( {x,A^{{\prime }} = A_{1} \cup A_{2} \cup \{ z\} } \right). $$

when i = j we have,

$$ T_{i}^{j} = \frac{{\left( {n_{i} kT_{i} + \varDelta n_{i}^{j} + k_{i} } \right)}}{{\left( {n_{i} + 1} \right)k}} $$

and when,

$$ T_{i}^{j} = T_{i} - \Delta n_{i}^{j} /n_{i} k $$

Therefore we have,

$$ \begin{aligned} {\text{f}}_{\text{ENN}} & = \arg_{j \in 1,2, \ldots ,N} { \hbox{max} }\sum\limits_{i = 1}^{N} {\left( {T_{i}^{j} - T_{i} } \right)} \\ {\text{f}}_{\text{ENN}} & = \arg_{j \in 1,2, \ldots ,N} { \hbox{max} }\left\{ {\left( {T_{i}^{j} - T_{i} } \right)_{i = j} + \sum\limits_{i \ne 1}^{N} {\left( {T_{i}^{j} - T_{i} } \right)} } \right\} \\ \end{aligned} $$

The ENN decision rule can be formulated as:

$$ f_{ENN} = \arg_{j \in 1,2, \ldots ,N} \hbox{max} \left\{ {\Delta n_{j} + k_{j} - kT_{j} } \right\} $$

3 Experimental Design

3.1 Face Datasets

3.1.1 ORL (Olivetti Research Laboratory) Dataset

figure h

The dataset consists of 40 subjects with 10 distinct images per subject, totaling to 400 images. This dataset is created specifically for Face Recognition. This dataset consists of very diverse images, captured under various lighting conditions. The dataset also captures a wide range of facial expressions which makes it a good choice for unconstrained face recognition (pose, expression, and illumination invariant) applications.

3.1.2 Faces94

This dataset consists of 153 subjects with 20 images per subject, totaling to 3060 images. The dataset consists of 133 male and 20 female subjects. The images are taken from a fixed distance by the camera under the same lighting conditions, so there are no scale or illumination variations. The subjects are speaking so, there are considerable expression variations. So, this dataset is generally preferred for expression invariant applications.

figure i

3.1.3 Grimace

figure j

This dataset consists of 18 subjects with 20 images per subject, totaling to 360 images. All the images of a subject are taken in a single session with a 0.5-s interval between two consecutive image captures. During the session, subjects try to make grimaces by varying their poses and facial expressions. So, this dataset is generally preferred for pose and expression invariant applications.

4 Experimental Results and Visualization

Various experiments were carried out in order to evaluate the performance of our proposed system. We used Accuracy, Precision and Recall as the performance metrics. We compared the results obtained from different dense feature descriptors. We also compared the results obtained from the dense descriptors with their traditional counterparts I.e. we compared the results of DSIFT [9] with SIFT [1], DSURF [5] with SURF [2] and DORB with ORB [3] descriptor.

4.1 Dense SIFT

The traditional SIFT descriptor fails to describe an ill-illuminated, ill-oriented image properly [9]. Actually the SIFT detector is not able to generate enough number of keypoints for such an image. DSIFT detector increases the number of keypoints in the image by making use of regular image grid points as interest points and passes these new keypoints to the DSIFT descriptor [9]. This is depicted in the figure below. The DSIFT detector takes a parameter which determines the grid size used to represent the input images. It’s value is dependent on the training dataset. We tuned this parameter to achieve the optimal results. For the ORL dataset grids containing squares of size 5 pixel × 5 pixel gave the best results. For the Faces94 dataset grids containing squares of size 4 pixel × 4 pixel produced the best results. Whereas for Grimace dataset grids containing squares of 3 pixel × 3 pixel gave optimal results.

figure k

4.2 Dense SURF

The classical SURF descriptor fails to describe an ill-illuminated, ill-oriented image properly [5]. SURF detector is not able to generate enough number of keypoints for such an image. DSURF detector increases the number of keypoints in the image by making use of regular grid points as keypoints and passes these new keypoints to the DSURF descriptor [5]. This is depicted in the figure below. The dense SURF descriptor takes a parameter which determines the grid size used to represent the input images. Its value is dependent on the training dataset. We tuned this parameter to achieve the optimal results. For the ORL dataset grids containing squares of size 11 pixel × 11 pixel gave the best results. For the Faces94 dataset grids containing squares of size 10 pixel × 10 pixel produced the best results whereas for Grimace dataset grids containing squares of size 15 pixel × 15 pixel gave optimal results.

figure l

4.3 Dense ORB

ORB employs a FAST detector which is rotation invariant [3]. But, it fails to incorporate illumination invariance. Because of this, ORB fails if the images are ill-illuminated or have a low contrast. DORB is able to counter this by using regular image grid points as keypoints. This way it can detect keypoints even in a poorly lit image. This is depicted in the figure below. The FAST detector present in DORB, takes a parameter which determines the grid size used to represent the input images. For the ORL, Faces94 and Grimace datasets grids containing squares of size 3 pixel × 3 pixel produced optimal results.

figure m

4.4 Performance Evaluation

On the ORL dataset, the proposed DSIFT descriptor and DORB descriptor performed quite well. DSIFT gave better results than DORB. These two descriptors surpassed all other descriptors. DSIFT outperformed DORB by an accuracy margin of 0.54% and DSURF by an accuracy margin of 16.96%. Also, DSIFT outperformed SIFT by an accuracy margin of 5.41%, DSURF outperformed SURF by an accuracy margin of 1.39% and DORB outperformed ORB by an accuracy margin of 3.26%.

On the Faces94 dataset, the proposed DSIFT descriptor and DORB descriptor performed quite well. DORB gave better results than DSIFT. DORB outperformed DSIFT by an accuracy margin of 0.79% and DSURF by an accuracy margin of 13.56%. Also, DSIFT outperformed SIFT by an accuracy margin of 4.02%, DSURF outperformed SURF by an accuracy margin of 0.23% and DORB outperformed ORB by an accuracy margin of 1.48%.

On the Grimace dataset, the proposed DSIFT descriptor and DORB descriptor performed quite well. DSIFT gave better results than DORB. DSIFT outperformed DORB by an accuracy margin of 1.89% and DSURF by an accuracy margin of 17.21%. Also, DSIFT outperformed DSIFT by an accuracy margin of 6.35%, DSURF outperformed SURF by an accuracy margin of 1.01% and DORB outperformed ORB by an accuracy margin of 2.3%.

Feature descriptors

Accuracy (%)

Precision (%)

Recall (%)

Dense SIFT

94.25

92.10

97.25

Dense SURF

77.29

78.76

84.30

Dense ORB

93.71

91.27

95.00

SIFT

88.84

89.73

91.34

SURF

75.90

77.90

81.14

ORB

90.45

90.89

93.67

Feature descriptors

Accuracy (%)

Precision (%)

Recall (%)

Dense SIFT

97.36

97.72

98.11

Dense SURF

84.59

83.20

90.23

Dense ORB

98.15

98.07

99.44

SIFT

93.34

92.50

95.00

SURF

84.36

84.20

88.47

ORB

96.67

96.23

96.16

Feature descriptors

Accuracy (%)

Precision (%)

Recall (%)

Dense SIFT

98.44

96.85

99.32

Dense SURF

81.23

83.48

88.91

Dense ORB

96.55

94.67

97.30

SIFT

92.09

93.43

94.17

SURF

80.22

79.65

84.73

ORB

94.25

94.5

95.23

4.5 Performance Comparison

figure n

5 Conclusion and Future Work

This paper introduces a novel pipeline for Face Recognition. It employs dense feature descriptors for feature extraction and extended nearest neighbor classifier for the classification task. This paper also provides a detailed comparison of various dense feature descriptors (DSIFT, DSURF, and DORB) with themselves and with their classical counterparts (SIFT, SURF, and ORB). Upon extensive experimentation, we are able to conclude that DSIFT and DSURF surpass other feature descriptors in terms of accuracy, precision, and recall. Therefore, these are better suited for face recognition.

In future, we would focus on making the model more robust and making it work under unconstrained scenarios i.e. invariant to scaling, illumination, occlusion, and age.