Dynamic Analysis of Composite Cylinders Using 3-D Degenerated Shell Elements

Abstract

This paper deals with the formulation of an 8-noded degenerated shell finite element for modeling and analysis of laminated composite shell structures. A MATLAB code has been developed based on the formulation to analyze the composite shell structures. The formulation is capable of solving both plate and shell structures. Use of degenerated shell elements allows the formulation to be used for any type of shells with various shapes and thickness ratios. The formulation is also capable of solving isotropic and laminated composite materials. The formulation developed has been validated with the results available in open literatures and software (ANSYS).

1 Introduction

Shells with variable thickness have extensively been used in many fields such as aerospace, rocket, aviation, and submarine technology. Over the years much research has been conducted in attempts to produce precise, competent, and reliable shell elements. Various shell theories have been developed, over the years, based on the thickness of the shells.

Three separate classes of shell elements have been widely used for analyzing shell structures: flat elements, curved shell elements, and degenerated shell elements. Flat, plate-like elements which approximate the curved shell by a faceted surface, hence sometimes called facet elements, show completely uncoupled behavior between in-plane stretching and bending. The coupling between in-plane stretching and bending only appears indirectly by linking adjacent elements through the nodal degrees of freedom. These elements are not preferred due to shortcomings such as the absence of curvature of the elements within the element. Also, slope discontinuity between neighboring plate elements can generate bending moments in the sections of structure where they do not exist. The interior of the individual elements will not have any coupling between bending effects and membrane effects due to curvature of shell. Curved shell elements are founded on several shell theories which are also quite popular. These elements have various limitations due to fact that the shell theories are not consistent with each other. Also, it is very difficult to find appropriate deformation idealizations where truly strain-free rigid body movements are allowed. The degenerated shell element is not based on any of the available shell theories and can be applied over a wide range of thicknesses and curvatures. The degenerate solid approach is used to develop this element, which is formulated on Reissner–Mindlin assumptions where, the shear deformation and rotary inertia effect of the shell is considered in the formulation and the 3D field is reduced to a 2D field in form of mid-surface nodal variables.

In the late sixties, Ahmad et al. [1] developed a Mindlin-type, degenerated, curved shell element which is quite competent as well as effortless. It can be used for any arbitrary shape and does not depend upon any specific shell theory. In order to eliminate shear and membrane locking, Zeinkiewicz et al. [2] improved the degenerated shell element developed by Ahmad et al. [1], by reducing the order of numerical integration. Huang & Hinton [3] presented a new nine node degenerated shell element formulation. To avoid locking phenomena, they proposed the assumed strain method where an enhanced interpolation of the transverse shear strains in the natural co-ordinate system is used. The nine-node degenerated shell element formulation developed by Huang and Hinton [3] was later extended by Jayashankar et al. [4] to conduct free vibration analysis of thick laminated composites. Because the degenerated shell element formulation works well for both thick and thin shells, nine-noded degenerated shell element was preferred over conventional solid elements for the modeling and analysis of laminated composite shell structures. Balamurugan and Narayanan [5] developed a nine-noded degenerate shell finite element model for the vibration and active vibration control of piezo-laminated composite plates and shells bonded with piezoelectric sensor and actuator layers.

Most of the research that has been done on degenerated shells is focused on the static analysis of structures such as dams, tanks, and dome, etc. Very less work is done on dynamic analysis using degenerated shells and fewer on the dynamic analysis of composite structures using degenerated shells. The main objective of this paper is to develop a MATLAB code for dynamic analysis of composite cylindrical shell using 3-D degenerated element which can accurately solve different types of shells and plates with both isotropic and composite materials.

2 Methodology

Some of the important aspects of the standard finite element scheme under plane strain platform are outlined in the following sub-sections.

2.1 3-D Degenerated Shell Element

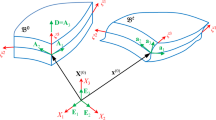
In present study, we have considered an 8-noded degenerated shell element with natural coordinate system ($\xi ,\eta ,\zeta$), which is defined by the element geometry and not by the element orientation in the global coordinate system. The natural elements are scaled such that the sides of the parent elements are defined by $\xi = \pm 1,\eta = \pm 1$ and $\zeta = \pm 1$. A 16-noded solid shell element and equivalent 8-noded degenerated shell element is shown in Fig 1.

Fig. 1

A 16-noded solid shell element and equivalent 8-noded degenerated shell element

Above element is similar to 8-noded serendipity element so we can use same shape function as the serendipity element.

$$ \begin{array}{*{20}l} \begin{aligned} & N_{1} = \frac{{\left( {1 - \xi } \right)\left( {1 - \eta } \right)\left( { - \xi - \eta - 1} \right)}}{4}; \\ & N_{2} = \frac{{\left( {1 - \xi^{2} } \right)\left( {1 - \eta } \right)}}{2}; \\ & N_{3} = \frac{{\left( {1 + \xi } \right)\left( {1 - \eta } \right)\left( {\xi - \eta - 1} \right)}}{4}; \\ & N_{4} = \frac{{\left( {1 + \xi } \right)\left( {1 - \eta^{2} } \right)}}{2}; \\ \end{aligned} \hfill & \begin{aligned} & N_{5} = \frac{{\left( {1 + \xi } \right)\left( {1 + \eta } \right)\left( {\xi + \eta - 1} \right)}}{4}; \\ & N_{6} = \frac{{\left( {1 - \xi^{2} } \right)\left( {1 + \eta } \right)}}{2}; \\ & N_{7} = \frac{{\left( {1 - \xi } \right)\left( {1 + \eta } \right)\left( { - \xi + \eta - 1} \right)}}{4}; \\ & N_{8} = \frac{{\left( {1 - \xi } \right)\left( {1 - \eta^{2} } \right)}}{2}; \\ \end{aligned} \hfill \\ \end{array} $$

(1)

A point in the element can be represented as

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \sum {N_{i} (\xi ,\eta )\left[ {\left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\} + \frac{\zeta }{2}V_{3i} } \right]} $$

(2)

where,

$$ \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\} = \frac{1}{2}\left[ {\left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{\text{top}} + \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{\text{bottom}} } \right]\quad {\text{and}}\quad V_{3i} = \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{\text{top}} - \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}_{\text{bottom}} $$

(3)

For thin structures, it is convenient to replace $V_{3i}$ by a unit vector $v_{3i}$. Thus equation changes to

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \sum {N_{i} (\xi ,\eta )} \left[ {\left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\} + \frac{\zeta }{2}t_{i} v_{3i} } \right] $$

(4)

where, $t_{i}$ is the thickness of the shell at node $i$.

The displacement field, in the element, can be represented as

$$ \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \sum {N_{i} (\xi ,\eta )} \left[ {\left\{ {\begin{array}{*{20}c} {u_{i} } \\ {v_{i} } \\ {w_{i} } \\ \end{array} } \right\} + \frac{{\zeta t_{i} }}{2}[\begin{array}{*{20}c} { - v_{2i} } & {v_{1i} } \\ \end{array} ]\left\{ {\begin{array}{*{20}c} \alpha \\ \beta \\ \end{array} } \right\}} \right] $$

(5)

where $v_{2i} ,v_{1i} ,\alpha$ and $\beta$ are unit vectors in y and x directions and rotations in x and y directions respectively as shown in Fig. 2.

Fig. 2

Local and global coordinates of a middle surface shell element

2.2 Strain Definitions

Strain definitions are needed to find strain displacement matrix $\left[ B \right]$. Since the elements have different coordinate system from global coordinates, we need strains in local coordinates by converting global strains to local strains.

$$ \left\{ {\varepsilon^{\prime } } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\prime } } \\ {\varepsilon_{y}^{\prime } } \\ {\gamma_{xy}^{\prime } } \\ {\gamma_{yz}^{\prime } } \\ {\gamma_{xz}^{\prime } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u^{\prime } }}{{\partial x^{\prime } }}} \\ {\frac{{\partial v^{\prime } }}{{\partial y^{\prime } }}} \\ {\frac{{\partial u^{\prime } }}{{\partial y^{\prime } }} + \frac{{\partial v^{\prime } }}{{\partial x^{\prime } }}} \\ {\frac{{\partial v^{\prime } }}{{\partial z^{\prime } }} + \frac{{\partial w^{\prime } }}{{\partial y^{\prime } }}} \\ {\frac{{\partial u^{\prime } }}{{\partial z^{\prime } }} + \frac{{\partial w^{\prime } }}{{\partial x^{\prime } }}} \\ \end{array} } \right\} $$

(6)

Also

$$ \frac{{\partial u^{\prime } }}{{\partial x^{\prime } }} = \frac{{\partial u^{\prime } }}{\partial x}\frac{\partial x}{{\partial x^{\prime } }} + \frac{{\partial u^{\prime } }}{\partial y}\frac{\partial y}{{\partial x^{\prime } }} + \frac{{\partial u^{\prime } }}{\partial z}\frac{\partial z}{{\partial x^{\prime } }}\quad {\text{and}}\quad \frac{{\partial u^{\prime } }}{\partial x} = \frac{\partial u}{\partial x}\frac{{\partial u^{\prime } }}{\partial u} + \frac{\partial v}{\partial x}\frac{{\partial u^{\prime } }}{\partial v} + \frac{\partial w}{\partial x}\frac{{\partial u^{\prime } }}{\partial w} $$

where $\frac{\partial x}{{\partial x^{{\prime }} }},\frac{\partial y}{{\partial x^{{\prime }} }},\frac{\partial z}{{\partial x^{{\prime }} }},\frac{\partial x}{{\partial y^{{\prime }} }},\frac{\partial y}{{\partial y^{{\prime }} }}, \ldots .$ and $\frac{{\partial u^{{\prime }} }}{\partial u},\frac{{\partial u^{{\prime }} }}{\partial v},\frac{{\partial u^{{\prime }} }}{\partial w},\frac{{\partial v^{{\prime }} }}{\partial u},\frac{{\partial v^{{\prime }} }}{\partial v}, \ldots .$ are direction cosines between global and local coordinate system.

Solving Eq. (6) using Eq. (7), we get

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\prime } } \\ {\varepsilon_{y}^{\prime } } \\ {\gamma_{xy}^{\prime } } \\ {\gamma_{yz}^{\prime } } \\ {\gamma_{xz}^{\prime } } \\ \end{array} } \right\} = \mathop {\left[ {\begin{array}{*{20}c} {l_{x}^{2} } & {m_{x}^{2} } & {n_{x}^{2} } & {l_{x} m_{x} } & {m_{x} n_{x} } & {l_{x} n_{x} } \\ {l_{y}^{2} } & {m_{y}^{2} } & {n_{y}^{2} } & {l_{y} m_{y} } & {m_{y} n_{y} } & {l_{y} n_{y} } \\ {2l_{x} l_{y} } & {2m_{x} m_{y} } & {2n_{x} n_{y} } & {l_{x} m_{y} + l_{y} m_{x} } & {m_{x} n_{y} + m_{y} n_{x} } & {l_{x} n_{y} + l_{y} n_{x} } \\ {2l_{y} l_{z} } & {2m_{y} m_{z} } & {2n_{y} n_{z} } & {l_{y} m_{z} + l_{z} m_{y} } & {m_{y} n_{z} + m_{z} n_{y} } & {l_{y} n_{z} + l_{z} n_{y} } \\ {2l_{x} l_{z} } & {2m_{x} m_{z} } & {2n_{x} n_{z} } & {l_{z} m_{x} + l_{x} m_{z} } & {m_{z} n_{x} + m_{x} n_{z} } & {l_{z} n_{x} + l_{x} n_{z} } \\ \end{array} } \right]}\limits_{\left[ T \right]} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} $$

(7)

Here $l_{x} ,l_{y} ,l_{z} ,m_{x} , \ldots$ are the direction cosines which can be calculated using the Jacobian matrix of the element.

$$ \left( {n_{x} ,n_{y} ,n_{z} } \right) = \left( {\frac{dx}{d\xi },\frac{dy}{d\xi },\frac{dz}{d\xi }} \right)\times\left( {\frac{dx}{d\eta },\frac{dy}{d\eta },\frac{dz}{d\eta }} \right) $$

(8)

$$ \left( {l_{x} ,l_{y} ,l_{z} } \right) = \frac{{\left( {n_{x} ,n_{y} ,n_{z} } \right)}}{{\left| {\left( {n_{x} ,n_{y} ,n_{z} } \right)} \right|}} $$

(9)

$$ \left( {m_{x} ,m_{y} ,m_{z} } \right) = \left( {n_{x} ,n_{y} ,n_{z} } \right)\times\left( {l_{x} ,l_{y} ,l_{z} } \right) $$

(10)

Global strains can be written as

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{z} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} = \mathop {\left[ {\begin{array}{*{20}c} {\frac{\partial \xi }{\partial x}} & {\frac{\partial \eta }{\partial x}} & {\frac{\partial \zeta }{\partial x}} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{\partial \xi }{\partial y}} & {\frac{\partial \eta }{\partial y}} & {\frac{\partial \zeta }{\partial y}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{\partial \xi }{\partial z}} & {\frac{\partial \eta }{\partial z}} & {\frac{\partial \zeta }{\partial z}} \\ {\frac{\partial \xi }{\partial y}} & {\frac{\partial \eta }{\partial y}} & {\frac{\partial \zeta }{\partial y}} & {\frac{\partial \xi }{\partial x}} & {\frac{\partial \eta }{\partial x}} & {\frac{\partial \zeta }{\partial x}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{\partial \xi }{\partial z}} & {\frac{\partial \eta }{\partial z}} & {\frac{\partial \zeta }{\partial z}} & {\frac{\partial \xi }{\partial y}} & {\frac{\partial \eta }{\partial y}} & {\frac{\partial \zeta }{\partial y}} \\ {\frac{\partial \xi }{\partial z}} & {\frac{\partial \eta }{\partial z}} & {\frac{\partial \zeta }{\partial z}} & 0 & 0 & 0 & {\frac{\partial \xi }{\partial x}} & {\frac{\partial \eta }{\partial x}} & {\frac{\partial \zeta }{\partial x}} \\ \end{array} } \right]}\limits_{{\left[ {\text{Jac}} \right]}} \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial \xi }} \\ {\frac{\partial u}{\partial \eta }} \\ {\frac{\partial u}{\partial \zeta }} \\ {\frac{\partial v}{\partial \xi }} \\ {\frac{\partial v}{\partial \eta }} \\ {\frac{\partial v}{\partial \zeta }} \\ {\frac{\partial w}{\partial \xi }} \\ {\frac{\partial w}{\partial \eta }} \\ {\frac{\partial w}{\partial \zeta }} \\ \end{array} } \right\} $$

(11)

where,

$$ \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial \xi }} \\ {\frac{\partial u}{\partial \eta }} \\ {\frac{\partial u}{\partial \zeta }} \\ {\frac{\partial v}{\partial \xi }} \\ {\frac{\partial v}{\partial \eta }} \\ {\frac{\partial v}{\partial \zeta }} \\ {\frac{\partial w}{\partial \xi }} \\ {\frac{\partial w}{\partial \eta }} \\ {\frac{\partial w}{\partial \zeta }} \\ \end{array} } \right\} = \sum\limits_{i = 1}^{8} {\mathop {\left[ {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial \xi }} & 0 & 0 & { - \frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} l_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} l_{1i} }}{2}} \\ {\frac{{\partial N_{i} }}{\partial \eta }} & 0 & 0 & { - \frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} l_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} l_{1i} }}{2}} \\ 0 & 0 & 0 & { - \frac{{N_{i} t_{i} l_{2i} }}{2}} & {\frac{{N_{i} t_{i} l_{1i} }}{2}} \\ 0 & {\frac{{\partial N_{i} }}{\partial \xi }} & 0 & { - \frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} m_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} m_{1i} }}{2}} \\ 0 & {\frac{{\partial N_{i} }}{\partial \eta }} & 0 & { - \frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} m_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} m_{1i} }}{2}} \\ 0 & 0 & 0 & { - \frac{{N_{i} t_{i} m_{2i} }}{2}} & {\frac{{N_{i} t_{i} m_{1i} }}{2}} \\ 0 & 0 & {\frac{{\partial N_{i} }}{\partial \xi }} & { - \frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} n_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \xi }\frac{{\zeta t_{i} n_{1i} }}{2}} \\ 0 & 0 & {\frac{{\partial N_{i} }}{\partial \eta }} & { - \frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} n_{2i} }}{2}} & {\frac{{\partial N_{i} }}{\partial \eta }\frac{{\zeta t_{i} n_{1i} }}{2}} \\ 0 & 0 & 0 & { - \frac{{N_{i} t_{i} n_{2i} }}{2}} & {\frac{{N_{i} t_{i} n_{1i} }}{2}} \\ \end{array} } \right]}\limits_{{\left[ {\partial N} \right]}} } \left\{ {\begin{array}{*{20}c} {u_{i} } \\ {v_{i} } \\ {w_{i} } \\ {\alpha_{i} } \\ {\beta_{i} } \\ \end{array} } \right\} $$

(12)

2.3 Strain Displacement Matrix

Strain displacement matrix $\left[ B \right]$ can be defined as

$$ \left[ B \right] = \left[ T \right]\left[ {\text{Jac}} \right]\left[ {\partial N} \right] $$

(13)

2.4 Stress Strain Relationship Matrix

Stress strain relationship matrix $\left[ D \right]$ is considered in local coordinate system and taken as

$$ \left[ D \right] = \frac{E}{{\left( {1 - \upsilon^{2} } \right)}}\left[ {\begin{array}{*{20}c} 1 & \upsilon & 0 & 0 & 0 \\ \upsilon & 1 & 0 & 0 & 0 \\ 0 & 0 & {\frac{{\left( {1 - \upsilon } \right)}}{2}} & 0 & 0 \\ 0 & 0 & 0 & {\frac{{K_{s} \left( {1 - \upsilon } \right)}}{2}} & 0 \\ 0 & 0 & 0 & 0 & {\frac{{K_{s} \left( {1 - \upsilon } \right)}}{2}} \\ \end{array} } \right] $$

(14)

where $E,\upsilon$ and $K_{s}$ are modulus of elasticity, Poisson’s ratio and shear correction factor for the given Isotropic material.

For orthotropic materials, the stress strain relationship matrix $\left[ D \right]$ will be taken as

$$ \left[ D \right] = \frac{1}{{1 - \upsilon_{12} \upsilon_{21} }}\left[ {\begin{array}{*{20}c} {E_{1} } & {\upsilon_{21} E_{1} } & 0 & 0 & 0 \\ {\upsilon_{12} E_{2} } & {E_{2} } & 0 & 0 & 0 \\ 0 & 0 & {G_{12} } & 0 & 0 \\ 0 & 0 & 0 & {K_{s} G_{13} } & 0 \\ 0 & 0 & 0 & 0 & {K_{s} G_{23} } \\ \end{array} } \right] $$

(15)

2.5 Stiffness Matrix

Stiffness matrix $\left[ K \right]$ can be expressed as

$$ \left[ K \right] = \iiint {\left[ {B^{T} } \right]\left[ D \right]\left[ B \right]\left| J \right|d\xi d\eta d\zeta } $$

(16)

2.6 Mass Matrix

Mass matrix $\left[ M \right]$ is expressed as

$$ \left[ M \right] = \iiint {\rho N^{T} N\left| J \right|}d\xi d\eta d\zeta $$

(17)

where $\rho$ is the density of material. And

$$ \left[ N \right] = \sum\limits_{i = 1}^{8} {\left[ {\begin{array}{*{20}c} {N_{i} } & 0 & 0 & { - \frac{{N_{i} t_{i} l_{2i} }}{2}} & {\frac{{N_{i} t_{i} l_{1i} }}{2}} \\ 0 & {N_{i} } & 0 & { - \frac{{N_{i} t_{i} m_{2i} }}{2}} & {\frac{{N_{i} t_{i} m_{1i} }}{2}} \\ 0 & 0 & {N_{i} } & { - \frac{{N_{i} t_{i} n_{2i} }}{2}} & {\frac{{N_{i} t_{i} n_{1i} }}{2}} \\ \end{array} } \right]} $$

(18)

2.7 Free Vibration

Free vibration equation of the structure, without damping, is given as

$$ \left[ M \right]\ddot{x} + \left[ K \right]x = 0 $$

(19)

2.8 Numerical Integration

We have considered different Gauss points for bending and shear to avoid shear locking and to get more accurate results.

2.8.1 Isotropic Material

For Isotropic materials, we have taken 3 Gauss points each in ξ and η directions and two Gauss points in ζ direction in case of bending. For shear, we have taken 2 Gauss points each in ξ and η directions and one Gauss point in ζ direction.

2.8.2 Composite Material

Composite laminated shell elements require an independent quadrature for each lamina since the material property (stress-strain relationship matrix [D]) depends upon the fiber orientation. Thus if ζ_l and ζ_l+1 define the thickness position of the lth layer, then

$$ \zeta = \zeta_{l} + \frac{{t_{l} }}{t}\left( {1 + \zeta^{\prime } } \right)\,\,{\text{and}}\,\,d\zeta = \frac{{t_{l} }}{t}d\zeta^{\prime } $$

(20)

where t_l is the layer thickness and $- 1 \le \zeta^{{\prime }} \le 1$ for $\zeta_{l} \le \zeta \le \zeta_{l + 1}$.

For each lamina, we have taken 3 Gauss points each in ξ and η directions and two Gauss points in ζ direction in case of bending. For shear, we have taken 2 Gauss points each in ξ and η directions and one gauss point in ζ direction.

3 Results and Discussions

3.1 Convergence Study

3.1.1 Square Plate

A convergence study is performed in order to determine the required number of mesh division N_x (number of divisions in x-direction) × N_y (number of divisions in y-direction) at which the objective values converge. Thickness ratio (a/h) is assumed to be 5. The problem considered here is a cross ply (0/90/90/0) of square cross section and having simply supported boundary conditions which is defined as

$$ \begin{aligned} & v = w = \beta = 0\,\,{\text{at}}\,x = 0,a \\ & u = w = \alpha = 0\,\,{\text{at}}\,y = 0,b \\ \end{aligned} $$

The elastic properties of the lamina with respect to the material axes has been taken as E₁/E₂ = 10, G₁₂ = G₁₃ = 0.6 E₂, G₂₃ = 0.5 E₂, ν₁₂ = 0.25, and ρ = 1. Thickness ratio (a/h) is assumed to be 5.

Since it is clear form Table 1 that the program converges at 10 × 10, so we have taken mesh size as 10 × 10 for square plate.

Table 1 Non-dimensional frequency parameter $\bar{\omega } = \omega a^{2} /h\sqrt {\rho /E_{2} }$ of a simply supported (SSSS) square cross ply (0/90/90/0) plate. a/h = 5

3.1.2 Cylindrical Shell

A convergence study is performed in order to determine the required number of mesh division N_h (number of divisions in direction of height) × N_r (number of divisions in radial direction) at which the objective values converge. The problem considered here is an isotropic cylindrical shell having bottom side fixed which is defined as

$$ u = v = w = \alpha = \beta = 0\,{\text{at}}\,z = 0 $$

The material properties have been taken as E = 71 GPa, v = 0.33, and ρ = 2770 kg/m³. Height of tank is taken as 0.6 m, outer radius 0.15 m and thickness is taken as 1 mm.

From Table 2, it is clear that the program converges at 8 × 120, so we have taken mesh size as 8 × 120 for cylindrical shells.

Table 2 Natural Frequency (Hz) of Isotropic cylindrical shell

3.2 Validation of Results

The results obtained from MATLAB code, created for solving free vibration of isotropic and laminated composite plates and shells, are compared with the results available in open literature and are in good agreement with the literature available in open source.

We have compared our result with the natural frequencies of composite plate and isotropic circular cylinder, available in literatures and result generated by ANSYS.

3.2.1 Composite Plate

The problem considered here is a cross ply (0/90/90/0) of square cross section and having simply supported boundary conditions. The elastic properties of the lamina with respect to the material axes has been taken as E₁/E₂ = 10, G₁₂ = G₁₃ = 0.5 E₂, G₂₃ = 0.6 E₂, ν₁₂ = 0.25, and ρ = 1. Thickness ratio (a/h) is assumed to be 5.

Table 3 Non-dimensional frequency parameter $\bar{\omega } = \omega a^{2} /h\sqrt {\rho /E_{2} }$ of a simply supported (SSSS) square cross ply (0/90/90/0). a/h = 5

As we can see from Table 3, the results obtained for composite plates from present formulation are in good agreement with the results available in open literature.

3.2.2 Isotropic Cylindrical Shell

An Isotropic cylindrical shell of 0.6 m height, 0.15 m outer radius and 0.1 mm thickness is considered. We have assumed Aluminum as material with E = 71 GPa, $\upsilon$ = 0.33 and density as 2770 kg/m³. Bottom side of shell is assumed to be fixed and top is assumed to be free.

It is evident from Table 4 that the result obtained for isotropic cylindrical shell from present formulation are in good agreement with results available in open literature as well as the results obtained from software (ANSYS).

Table 4 Natural frequency (Hz) of isotropic cylindrical shell

The formulation developed based on 3-D degenerated shell elements has been validated by comparing results obtained for composite plates and isotropic shells. The results are in good agreement with open literature and software. Thus we conclude that the formulation is correct and is able to produce accurate results.

3.3 Parametric Studies

We have considered a laminated composite cylindrical shell with varying no of lamina, ply angle, and thickness of shell.

Height of cylindrical shell is taken as 0.6 m, outer radius is taken as 0.15 m and this thickness of shell is taken as 1 mm. Material properties are considered as E₁ = 45 GPa, E₂ = 10 GPa, $\upsilon_{12}$ = 0.3, G₁₂ = 5 GPa, G₂₃ = 4 GPa, G₁₃ = 5 GPa, and density is taken as 2000 kg/m³ (Table 5).

Table 5 Natural frequency (Hz) of composite cylindrical shell with thickness 1 mm

Now we have increased the thickness of the shell to study its effect on natural frequency. Height of cylindrical shell is taken as 0.6 m, outer radius is taken as 0.15 m and this thickness of shell is taken as 2 mm. Material properties are considered as E₁ = 45 GPa, E₂ = 10 GPa, $\upsilon_{12}$ = 0.3, G₁₂ = 5 GPa, G₂₃ = 4 GPa, G₁₃ = 5 GPa, and density is taken as 2000 kg/m³ (Table 6).

Table 6 Natural frequency (Hz) of composite cylindrical shell with thickness 2 mm

We have again increased the thickness of shell further. Height of cylindrical shell is taken as 0.6 m, outer radius is taken as 0.15 m and this thickness of shell is taken as 5 mm. Material properties are considered as E₁ = 45 GPa, E₂ = 10 GPa, $\upsilon_{12}$ = 0.3, G₁₂ = 5 GPa, G₂₃ = 4 GPa, G₁₃ = 5 GPa, and density is taken as 2000 kg/m³ (Table 7).

Table 7 Natural frequency (Hz) of composite cylindrical shell with thickness 5 mm

From parametric study, it is evident that the natural frequency of composite shell is increasing as we increase the thickness of the shell, which is consistent with our understanding of composite shells. Other parameters such as fiber orientation and no of lamina are also varied to understand their impact on natural frequency.

4 Conclusion

In the present work, a finite element formulation has been created for the dynamic analysis of laminated composite shell using 8-noded 3-D degenerated shell element. Present formulation is capable of analysis both isotropic and laminated composite shells of arbitrary geometry. The results generated so far are in good agreement with the results available in open literature as well as with the software generated results.

4.1 Future Work

Presented work can be extended to material and geometric non-linearity.

This work can also be extended to formulate Functionally Graded Materials (FGM).

Present work can be coupled with fluid formulation to formulated Fluid-Structure Interaction.