Keywords

1 Introduction

Wave propagation can be characterized by the localized region of the sharp gradient of field variable which changes its locations in space with time. This gives permission to recognize the unusual nature that could be suitable for ultrasonic nondestructive testing techniques. Guided-wave-based nondestructive techniques offer to evaluate the integrity of critical structures and to find out damage position, shape, and size [1, 2]. Several numerical techniques have been proposed to analyze the wave equations. Due to their relatively simple mathematical expressions and the possibility to be applied to the very large class of engineering problems, finite difference [3], boundary element [4], and finite element [2] based methods have been used by many authors for the simulation of guided Lamb waves. Finite element method (FEM) [2, 5] is a widespread numerical method used to simulate elastic guided wave propagation problem. Finite difference method (FDM) has also been used for the study of wave simulation and damage interaction by several researchers. Although FDM schemes are well situated for wave propagation in homogeneous media, however, the major limitation of the FDM schemes is that stiffness jumps due to continuously changing physical properties cause stability problems [6]. Furthermore, boundaries as well as discontinuities between different types of media lead to fairly accurate solutions and can generate severe errors [7]. With this in mind, more recently, Delsanto et al. have proposed the local interaction simulation approach (LISA) in combination with the sharp interface model [7]. Recently, customized elements and geometric multi-scale finite element method have been introduced to analyze various types of wave propagation problems [8]. The finite element method, which has been preferred for elastic wave propagation, is not suitable to simulate nonlinear waves or higher harmonics of propagating waves. A drastic increase of nodes for the simulation of nonlinear wave problems demands some necessary alteration in FEM which must be numerically efficient and straightforward.

In recent years, wavelet-based numerical methods gain much attention for solving partial differential equations. The major advantage of this approach allows one to examine a problem in different resolutions, simultaneously. In addition, wavelet-based schemes are efficient in problems comprising singularities and sharp transitions in solutions for limited zones of a computation domain. Initially, Beylkin et al. [9] employed the study of numerical computation based on wavelet. Several mathematicians and scientists have established the superiority of wavelet-based methods for solving elliptic partial differential equations [10, 11]. The adaptivity of wavelets is one of the leading advantages for the implementation of wavelets in numerical analysis [12, 13]. Liandrat and Tchamitchian have solved regularized 1D Burgers’ equation by using spatial wavelet approximation [14]. Later, Beylkin and Keiser [15], Vasilyev and Bowman [16], and Kumar and Mehra [17] have developed different wavelets-based algorithms and tested on 1D Burgers’ and advection–diffusion equations. Researchers have increased the usage of wavelets for solution of partial differential equations (PDEs) after the development of the lifting scheme by Swelden [17] and stable completion by Carnicer et al. [18]. A review of wavelet techniques for the solution of PDEs has been presented by Dahmen [19]. However, a very few researchers have applied the wavelet-based method for analyzing wave propagation problem. Hong and Kennett proposed wavelet-based method for the numerical modeling and simulation of elastic wave propagation in 2D media [20]. Chen and Yang et al. presented the wave motion analysis of short wave in one-dimensional structures [21]. Mitra and Gopalakrishnan proposed wavelet-based spectral finite element method (WSFEM) for simulation of elastic wave propagation in one- and two-dimensional situations [22]. In the literature, some researchers have used wavelets as basis function to solve PDEs but most researchers have applied the wavelet-based adaptive technique in finite difference schemes. These papers have presented the adaptive method for propagation of a single wave, but there is a need for different algorithms for more than one waves propagating with different velocities. Generation of higher harmonics due to material nonlinearity is not addressed in these papers.

Multi-scale modeling is one possible solution for higher harmonics in wave propagation simulation. Wavelet-based multi-scale method leads to fast and locally adaptive algorithms. The compactly supported refinable basis functions are main potential advantage of the wavelet [10, 11]. However, these methods are unable to compete with conventional finite element method. In this paper, proposed technique is inspired by the interesting paper by Krysl et al. [23].

This paper presents multi-scale adaptive approach for solving the wave propagation problem. In the proposed wavelet-based technique, FEM is preferred due to its capability to handle complex boundary and loading conditions instead of any other methods. This multi-scale transformation hierarchically filters out the less significant frequencies and offers an operative framework to retain the necessary frequencies of the wave. In this procedure, the finest level of the coefficient matrix is calculated once for the whole domain while the adaptively compressed coefficient matrix, which is very small compared to complete coefficient matrix, is used in every marching step of the solution. This paper is presenting wavelet-based nonstandard operator to improve finite element simulation of linear and nonlinear wave propagation in a large structure. We use nonstandard operator because it is more efficient than standard operator [24]. This will not only be useful to the structural health monitoring, but it can also be used where waves with higher harmonics move at different group velocities. A simple description of the nonstandard operator along with necessary algorithm and mathematical comments is provided to remove an execution headache connected with adaptive grid techniques. The algorithm is applied to 2D plane strain problem, but it is general and independent of domain dimensions.

2 Mathematical Formulation

2.1 Lamb Waves

In an elastic medium, elastic waves are defined as propagating disturbances that transport energy without any material transfer. Elastic waves of plane strain that exist in free plates are called Lamb waves. For an orthotropic and symmetrical plate, particle motion is often outlined through the elemental elastodynamic differential equation of wave

$$ \partial_{l} (C_{klmn} \partial_{n} w_{m} ) = \rho \partial_{t}^{2} w_{k} ,\quad \left( {k,l,m,n = 1,2} \right). $$
(1)

Substituting stress relation in governing equations and Lamb wave can be expressed as

$$ C_{L}^{2} \frac{{\partial^{2} u}}{{\partial x^{2} }} + (C_{L}^{2} - C_{T}^{2} )\frac{{\partial^{2} v}}{\partial x\partial y} + C_{T}^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }} + f_{x} = \frac{{\partial^{2} u}}{{\partial t^{2} }}, $$
(2(a))
$$ C_{L}^{2} \frac{{\partial^{2} v}}{{\partial y^{2} }} + (C_{L}^{2} - C_{T}^{2} )\frac{{\partial^{2} u}}{\partial x\partial y} + C_{T}^{2} \frac{{\partial^{2} v}}{{\partial x^{2} }} + f_{y} = \frac{{\partial^{2} v}}{{\partial t^{2} }}. $$
(2(b))

\( C_{L}^{2} = \frac{\lambda + 2\mu }{\rho } \) and \( C_{T}^{2} = \frac{\mu }{\rho } \) are longitudinal velocity and shear velocity, respectively, where \( \lambda = \frac{E\nu }{(1 + \nu )(1 - 2\nu )} \) and \( \mu = \frac{E}{2(1 + \nu )} \) are Lamé constants, E is Young’s modulus, and \( \nu \) is Poisson ratio. The 2D plane strain problem is discretized into the set of finite element equations as

$$ [K][u] + [M][\ddot{u}] = 0, $$
(3)

where \( [u] \) and \( [\ddot{u}] \) are unknown coefficient vectors. \( [K] \) and \( [M] \) are global stiffness and mass matrix, respectively.

2.2 Multi-scaling Using Wavelets

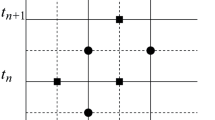
The idea of multi-scale exploration is to interpolate an unknown field at a coarse level with the assistance of supposed scaling functions. Any enhancement to initial approximation is accomplished by adding “details” rendered by basis functions referred to as wavelets. A multi-scaling analysis forms a sequence of closed subspaces to satisfy certain self-similarity relations as well as completeness and regularity relations. The basis functions in \( W_{j} \) are called wavelet functions. Wavelet functions are symbolized by \( \psi_{j,k} \). These scaling and wavelet functions are employed for wavelet-based multi-scaling. A function \( f \in L^{2} (R) \) is approximated by its projection \( P^{j} f \) onto the space Vj and the projection of f on \( W_{j} \) as \( Q^{j} f \), we have

$$ P^{j} f = P^{j - 1} f + Q^{j - 1} f. $$
(4)

If the coefficient vector of \( P^{j} f \) (or coefficients of scaling functions) is \( {\mathbf{C}}_{j} = \{ C_{j,0} , \ldots ,C_{j,v(j)} \}^{\text{T}} \) and coefficient vector of \( Q^{j} f \) (or coefficients of some wavelets) is \( {\mathbf{d}}_{j} = \{ d_{j,0} , \ldots ,d_{j,w(j)} \}^{\text{T}} \), then we can write wavelet transform as

$$ {\mathbf{C}}_{j} = [T_{j} ]\left[ {\frac{{{\mathbf{C}}_{j - 1} }}{{{\mathbf{d}}_{j - 1} }}} \right]. $$
(5)

The matrix \( [T_{j} ] \) is used to achieve next higher level by transforming scaling and detail coefficients of Vj−1 and Wj−1 spaces, respectively. In this paper, B-spline wavelet and Daubechies (D4) wavelet [25] are used for wave propagation.

2.3 Nonstandard Multi-scale Decomposition of Finite Element Matrix

Two observations can be made while solving some PDEs using the wavelet bases: (i) In theoretical terms, most of the available wavelet methods have stable Riesz basis and better condition number than FEM or FDM. (ii) But in practical applications, wavelet methods are not yet ready to compete with the traditional FEM approach. One important reason is while the FEM can always produce a sparse matrix with more regular sparsity patterns, use of wavelet bases does not produce such sparse matrices. But the combination of wavelets with other methods, such as FDM, FEM, and recently SEM [22], show good results. Here, we have used FEM discretization to derive a sparse matrix, as the FEM remains the most versatile tool to solve PDEs.

Let us consider a continuous wave field \( u(x,y) \) and \( v(x,y) \) for a source of excitation over 2D homogeneous medium. The approximation of the continuous wave field on the discrete domain is denoted by \( u^{j} \) and \( v^{j} \). It represents the discrete wave field that is obtained with a classic time–space finite element method for a sufficiently fine discretization of \( V_{j} \subset R^{2} \). The 2D wavelet transform cascades projections of the discrete wave field over different approximation grids \( V_{1} ,V_{2} ,V_{3} , \ldots ,V_{j} \) of increasing resolution.

In this multi-scale algorithm, we used NS operator proposed by Beylkin [26]. To the best of authors’ knowledge, no one researcher has used NS operator in wavelet–FEM coupling or wavelet–FDM coupling. It has been proved by Beylkin [26, 27] that NS operator is more efficient than the standard form of operator used by most of the researchers. In this paper, we have used NS operator in two-dimensional wavelet–finite element coupling technique. The finite element equations for the transient problem, Eq. 3, can be expressed in the expanded form as

$$ \left[ {\begin{array}{*{20}c} {\left[ {k_{uu}^{j} } \right]} & {\left[ {k_{uv}^{j} } \right]} \\ {\left[ {k_{vu}^{j} } \right]} & {\left[ {k_{vv}^{j} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u^{j} } \\ {v^{j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {f_{u}^{j} } \right]} \\ {\left[ {f_{v}^{j} } \right]} \\ \end{array} } \right]. $$
(6)

We can apply the wavelet transformation on the field variables of both the directions:

$$ \left[ {\begin{array}{*{20}c} {\left[ {T^{\text{T}} } \right]} & {[0]} \\ {[0]} & {\left[ {T^{\text{T}} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {k_{uu}^{j} } \right]} & {\left[ {k_{uv}^{j} } \right]} \\ {\left[ {k_{vu}^{j} } \right]} & {\left[ {k_{vv}^{j} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ T \right]} & {[0]} \\ {[0]} & {\left[ T \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {d^{1} } \right]} \\ {\left[ {u^{1} } \right]} \\ {\left[ {e^{1} } \right]} \\ {\left[ {v^{1} } \right]} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {T^{\text{T}} } \right]} & {[0]} \\ {[0]} & {\left[ {T^{\text{T}} } \right]} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {f_{u}^{j} } \right]} \\ {\left[ {f_{v}^{j} } \right]} \\ \end{array} } \right]. $$
(7)

The organization of the matrix after three-level transform of nonstandard form can be extended and expressed in the new notations as [24]

(8)

In order to solve it, Gines et al. [24] proposed nonstandard LU decomposition.

3 Results and Discussion

Elastic waves have been employed for identification of damage in the thin wall structures such as plates and pipes [5]. Guided Lamb waves are excited in the structures through narrowband burst signals. In order to evaluate the performance of wavelet-based multi-scale method. We considered an example in which a 50 × 50 mm2 homogeneous, isotropic aluminum plate with a density of 2700 kg/m3. The simulation of Lamb wave in this plate with 400 kHz central frequency is presented in Fig. 1. Contour plots of the displacement in the x-direction at three different time instants are well depicted in this figure.

Fig. 1
figure 1

Contour plots of the displacement in the x-direction at three different time frames for isotropic plate

Full size image

Nonlinear Lamb wave is more sensitive to small-scale damage identification. However, the investigations of the higher harmonics in propagating Lamb waves were ignored due to high computational cost. To see the efficiency of the wavelet-based method, higher harmonics are added in the Lamb wave and propagation of waves is observed. This study uses the following actuation function with 400 kHz central frequency:

$$ E(t) = \left\{ {\begin{array}{*{20}l} {f_{o} \sin (\Omega t)*\left( {\sin \left( {0.1\Omega t} \right)} \right)^{2} + 0.1f_{o} \sin (2*5\Omega t)*\left( {\sin (\Omega t)} \right)^{2} ,} \hfill & {t < {{10\pi } \mathord{\left/ {\vphantom {{10\pi }\Omega }} \right. \kern-0pt}\Omega }} \hfill \\ {0,} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right. $$

where \( \Omega \) is the frequency of excitation and \( E_{o} \) is the maximum amplitude. The excitation signal on a plate with a higher harmonics is shown in Fig. 2. An aluminum plate of 200 mm length and 2 mm thickness is used in the analysis. Poisson’s ratio = 0.3, density = 2700 kg/m3, and Young’s modulus E = 69 GPa are assumed as material properties. The Lamb wave in this material has longitudinal velocity CL = 5299 m/s and transverse velocity CT = 3135 m/s. The waves are actuated by employing pin forces applied to the left boundary of the plate. The excitation forces are parallel to the longitudinal (propagating) direction. In-phase pin forces are applied to the top and bottom edge nodes of the plate for excitation of fundamental symmetric (S0) modes, and the antisymmetric modes are propagated by imposing out-of-phase pin forces. In this paper, we considered the cases in which the pure S0 mode is excited. Ten cycles Hanning-window actuation is given through excitation function to deliver a limited cycle sinusoidal tone burst.

Fig. 2
figure 2

Excitation signal for Lamb wave with higher harmonics

Full size image

Higher frequency wave propagation problems demand enormous computer resources because of very large number of time integration steps and highly dense mesh. Generally, in the case of Lamb wave, 20 elements per wavelength are required but this is not sufficient for higher harmonic simulation. Figure 3 depicts the measured nodal displacement response of time-domain signals obtained using FEM simulation of the plate with 40, 80, and 120 elements per wavelength. It can be observed that higher harmonics are not properly visible in the response of the plate with 40 elements per wavelet. On the other hand, as shown in the same figure, higher harmonics are visible for 80 elements per wavelength.

Fig. 3
figure 3

Comparison of response of plate for 40, 80, and 120 elements per wavelength

Full size image

In the present analysis, B-spline and Daubechies (D4) wavelet are used to establish robustness and sensitivity of wavelet-based wave propagation method. To capture higher harmonics in the plates, FEM uses 17,080 uniformly distributed nodes while half of the FEM nodes are required after application of one level of wavelet transform. Nodal displacement response of plate received from B-spline and D4 wavelet transform at level 1 along with FEM results is demonstrated in Fig. 4. It establishes good agreement between conventional finite element and proposed wavelet-based method. It can be observed that B-spline wavelet produces response close to FEM results, while there is some deviation in the results of D4 wavelet. Further, we examined wavelet-based method at various levels of wavelet transform to find the level up to which this method can work efficiently. These results show some attenuation but wavelets are not eliminating higher frequency components of waves which are important in many analyses.

Fig. 4
figure 4

Comparison of higher harmonic Lamb waves plates response at wavelet transform level 1

Full size image

4 Conclusion

The spatial derivative operators in the wave equations are handled using multi-resolution transforms in a physical domain. We presented a wavelet-based framework to reduce the size of global stiffness matrix of finite element analysis which is becoming too large in the case of nonlinear wave propagation problem. Wavelet-based method is not only to develop the compressed stiffness matrix, but also to propagate higher harmonics of waves using least number of nodes and able to reduce the computational cost significantly. Without disturbing the programming advantages of FE regarding the implementation of boundary conditions and efficient numerical integration of interpolation functions, wavelet-based methods are able to reduce the size of matrix as much as one by a sixteenth of original FE matrix. These fundamental characteristics show that the wavelet-based method can be utilized for more complex wave propagation problems.