Keywords

1 Introduction

To understand boundary value problems for various practical geotechnical problems, understanding the behavior of soil under generalized loading conditions becomes paramount. The classical methodology of solving such problems is to formulate an analytical solution which becomes complex and cumbersome with an increase in difficulty. Numerical methods, with appropriate constitutive models, facilitate computation of a solution but require proper development, calibration, and refinement [6]. Capturing the various aspects of the behavior of soils gives rise to a large number of constitutive law, which is often too sophisticated to be used in practical problems. At the cost of simplicity, these constitutive laws define rigid mathematically derived parameters which are difficult to obtain through comprehensive experimental testing of soils [19]. As an alternative to classical elasto-plastic theory, the hypoplastic model was developed to describe the mechanical behavior of granular materials. The cornerstone of hypoplastic law is its simplicity and definition of parameters which can be derived experimentally, through routine laboratory test and its inherit nonlinearity which facilitates the localization of deformation. It is a rate type constitutive law which relates the strain rate to the stress rate and stems from rational mechanics in which a single equation can capture the different essential features of the behavior of granular materials [2, 13].

Pioneering attempts of physicist to simulate fracture with discrete models gave birth to Lattice methods. In parallel to these, methods, where each node corresponds to a single particle/aggregate, were developed called the Discrete Element Method Cundall and Strack [5]. Later, DEM became a prominent tool in micromechanics research with the introduction of interparticle shear and particle rotations [8]. As the mechanical behavior of granular materials depends upon the fabric/configuration characteristics and the properties of constituting soil particles, modeling of each grain particle in DEM directly simulates the microstructure of granular materials, and can be used to study different micro-level events such as initiation, formation, and growth of shear zones [10, 12, 14]. With DEM codes being widely available and implemented in parallel computing, cloud computing, and high-performance computing, the computation times have become significantly low.

The objective of this paper is to act as a bridge between the laboratory experiments, continuum and discontinuum mechanics. An attempt was made by Lin and Wu [11] to compare the DEM and hypoplasticity for 2D simulations with considerable success. Firstly, a brief theory of hypoplasticity and discrete element method is presented. Secondly, by simulating three-dimensional quasi-static drained triaxial tests, the contact law parameters are calibrated with results of experimental triaxial tests conducted on Karlsruhe sand. These calibrated contact parameters are then used in DEM simulations of routine geotechnical laboratory tests (gravity deposition, vibration table, compression) in order to find the critical parameters for hypoplastic constitutive law. Thirdly, using a MATLAB code, triaxial tests using hypoplastic parameters obtained using DEM simulations and from the literature are simulated. Finally, a comparison is presented of experimental results, DEM simulation results for triaxial tests, triaxial test simulated using hypoplastic parameters obtained from DEM simulations and triaxial test simulated using hypoplastic parameters obtained from the literature.

2 Theories (or Experiments, or Methodology)

2.1 Hypoplasticity

Non-linear tensor function establishes the core component of Hypoplasticity, instead of decomposition of deformation into elastic and plastic parts. With no distinction between elastic and plastic deformation, a single unique equation can be used for both loading and unloading. The equation is given in Herleand Gudehus [7] and used in this paper which relates stress rate tensor (T) with the stretching rate D, the Cauchy skeleton stress Ts and the void ratio e with a tensor function h given as:

$$ \dot{T}_{s} = h\left( {T_{s} ,D,e} \right) $$
(1)

In compression, the tensorial equation reduces to two scalar equations given as

$$ \begin{aligned} \dot{T}_{{s1}} & = f_{s} \frac{{\left( {T_{{s1}} + 2T_{{s2}} } \right)^{2} }}{{T_{{s1}}^{2} + 2T_{{s2}}^{2} }}\left[ {D_{1} + a^{2} \frac{{T_{{s1}} D_{1} + 2T_{{s2}} D_{2} }}{{\left( {T_{{s1}} + 2T_{{s2}} } \right)^{2} }}T_{{s1}} } \right. \\ & \quad \quad \quad \quad \quad \quad \quad \quad \left. { + f_{d} \frac{a}{3}\frac{{5T_{{s1}} - 2T_{{s2}} }}{{T_{{s1}} + 2T_{{s2}} }}\sqrt {D_{1}^{2} + 2D_{2}^{2} } } \right] \\ \end{aligned} $$
(2)
$$ \begin{aligned} \dot{T}_{{s2}} & = f_{s} \frac{{\left( {T_{{s1}} + 2T_{{s2}} } \right)^{2} }}{{T_{{s1}}^{2} + 2T_{{s2}}^{2} }}\left[ {D_{2} + a^{2} \frac{{T_{{s1}} D_{1} + 2T_{{s2}} D_{2} }}{{\left( {T_{{s1}} + 2T_{{s2}} } \right)^{2} }}T_{{s2}} } \right. \\ & \quad \quad \quad \quad \quad \quad \quad \quad \left. { + f_{d} \frac{a}{3}\frac{{4T_{{s2}} - T_{{s1}} }}{{T_{{s1}} + 2T_{{s2}} }}\sqrt {D_{1}^{2} + 2D_{2}^{2} } } \right] \\ \end{aligned} $$
(3)

The barotropic factor fb takes into consideration the increase of stiffness with an increase of the mean stress and is given as

$$ f_{s} = \frac{{h_{s} }}{n}\left( {\frac{{e_{i} }}{e}} \right)^{\beta } \frac{{1 + e_{i} }}{{e_{i} }}\left( {\frac{{3p_{s} }}{{h_{s} }}} \right)^{1 - n} \left[ {3 + a^{2} - a\sqrt {3 } \left( {\frac{{e_{i0} - e_{d0} }}{{e_{c0} - e_{d0} }}} \right)^{\alpha } } \right]^{ - 1} $$
(4)

Finally, fd is the pressure dependent relative void ratio and is computed as:

$$ f_{d} = \left( {\frac{{e - e_{d} }}{{e_{c} - e_{d} }}} \right)^{\alpha } $$
(5)

In total eight parameters are required to define a hypoplastic model which are, ei0, ec0, ed0, hs, n, a, α and β. A detailed description of a, α and β, can be found in [7].

2.2 Discrete Element Method

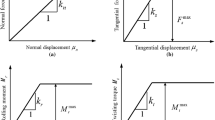
YADE, a three-dimensional discrete element software developed by the University of Grenoble, is used in this study [17]. It implements the soft particle approach to model the contact deformation and computes the force-displacement while tracking the positions, velocities, and accelerations of individual particles. These forces are divided into normal and tangential components which control the normal deformation, sliding, and rotation at contacts. With the total forces, the particles are pushed into new positions, and their accelerations are computed by integrating Newton’s equations of motion [10]. To complement the simplicity of hypoplastic law, a simple linear elastic normal contact with linear rotational moment law is proposed to simulate the response of spherical particles. The normal and tangential forces are proportional to the normal stiffness and tangential stiffness as (Fig. 1):

Fig. 1
figure 1

The response of the contact law and the grain size distribution of Karlsruhe sand

Full size image
$$ \overrightarrow {{F_{n} }} = k_{n} U\vec{N} $$
(6)
$$ \Delta \overrightarrow {{F_{s} }} = k_{s} \Delta \overrightarrow {{X_{s} }} $$
(7)

where U is the depth of penetration and ΔX is the tangential displacement vector. The stiffness parameters kn and ks are computed using the stiffness of the grain contact Ec and radii of the particles Ra and Rb respectively.

$$ k_{n} = E_{c} \frac{{2\,R_{a} R_{b} }}{{R_{a} + R_{b} }}\,{\text{and}}\,k_{s} = v_{c} E_{c} \frac{{2\,R_{a} R_{b} }}{{R_{a} + R_{b} }} $$
(8)

The frictional sliding is mobilized when the Mohr-Coulomb law is satisfied;

$$ \overrightarrow {{F_{s} }} \le \overrightarrow {{F_{n} }} \tan \left( \mu \right) $$
(9)

where, μ is the inter particle friction angle. To increase the rolling resistance of pure spheres, simple linear rotational moment law is introduced. Due to the normal forces, the rotation of the particles is arrested, resisting the rotation as

$$ \Delta M = k_{r} \Delta \vec{\omega } $$
(10)

Iwashita and Oda [8] related the rotational stiffness kr to the tangential stiffness ks as

$$ k_{r} = \beta k_{s} R_{a} R_{b} $$
(11)

A dimensionless rotation coefficient is introduced to control the moment of rotation (similar to Mohr–Coulomb sliding),

$$ \overrightarrow {\text{M}} \le \eta \frac{{R_{a} + R_{b} }}{2}\overrightarrow {{F_{n} }} $$
(12)

As compared to other discrete models incorporating contact moments, YADE is designed primarily for 3D simulations where rolling resistance is an independent parameter; rotations are described using quaternions and grain shape coefficient is not included [18]. In a total of five micromechanical parameters are required for discrete simulations Ec, μ, νc, η, β; along with ρ (density of particles) and damping.

2.3 Calibration of Contact Parameters

The most important part of any simulation is the calibration of the underlying law with experimental/physical results. The contact parameters were calibrated using the corresponding triaxial test experimentally conducted on Karlsruhe sand by Kolymbas and Wu [9]. Each component of the contact law affects the macroscopic response of the material depicted in the stress-strain and volume change curves as shown in Fig. 2 [3, 16]. In numerical simulations, a cloud of 10,000 particles was created in a cuboidal space of 0.25 cm × 0.25 cm × 0.75 cm space (aspect ratio of 3) with periodic boundaries. The particles were created based on the upscaled grain size distribution of Karlsruhe sand to decrease the time of simulation. The whole simulation process was divided into two main parts. In the first part, the cloud of the particle was isotropically compressed to the required confining stress under gravity-free conditions. If the required void ratio (e  = 0.53) was not reached during isotropic compression, the friction angle was reduced in order to assist the tighter rearrangement of particles. Once the confining stress was reached isotropically and the unbalanced forces reached low enough values, the friction angle was changed to the desired value, and the shearing in the form of axial strain application (a quasi-static condition with the loading of 1 mm/s) was started. Damping coefficient is kept at a low value of 0.1 in order to exclude the effect of damping on simulation results, yet large enough to dissipate the unbalanced energies and lower the time of simulation. Deviator stresses and corresponding volume change with axial strain were plotted at the constant interval during the simulation.

Fig. 2
figure 2

a Effect of contact parameters on the typical response of soil in the triaxial test; b numerical sample for the triaxial test in YADE; c velocity vectors at the final stage of shearing showing the slip plane

Full size image

2.4 Limiting Void Ratios at Zero Pressure

The limiting void ratio ei, ed and ec decrease exponentially with increase in ps following Eq. 13. The parameters hs and n control the pressure dependence of grain assembly. hs, which has the units of stress, is called the reference pressure and controls the slope of the void ratio confining pressure curve. Exponent n controls the non-linearity of the void ratio with confining pressure curve, which shows the increase in incremental stiffness with increasing confining stress. At zero ps, the limiting void ratio reaches a maximum value (ei0, ed0, and ec0) and each of them is determined using DEM in subsequent sections (Fig. 3).

Fig. 3
figure 3

Numerical simulation of a gravity deposition test (left), boundary conditions and sample for minimum void ratio test (right)

Full size image
$$ \frac{{e_{i} }}{{e_{i0} }} = \frac{{e_{c} }}{{e_{c0} }} = \frac{{e_{d} }}{{e_{d0} }} = \exp \left[ { - \left( {\frac{{3p_{s} }}{{h_{s} }}} \right)^{n} } \right] $$
(13)

2.4.1 Maximum Void Ratio at Zero Pressure (ei0)

ei0 is the loosest void ratio for a grain skeleton which is reached when a cloud of particles is isotropically compressed in a gravity-free space. As pure isotropic compression is difficult in the laboratory, it is almost impossible to determine the value of ei0 experimentally. DEM, on the other hand, provides control over the strain rate and gravitational forces in the system. Isotropic compression has been used extensively for numerical sample preparations, especially for subsequent triaxial testing. To compute ei0 for Karlsruhe sand, isotropic compression was simulated in a periodic cube of size 0.1 m. The contact parameters used were the same as calibrated in Sect. 2.3. By observing the force chains and void ratio with confining stress curve, 5 kPa was used as a limit to report ei0 values. Using the same compression curve, the values of hs and n were computed using the methodology given by Herle and Gudehus [7].

2.4.2 Critical Void Ratio at Zero Pressure (ec0)

In a laboratory test for determination of maximum void ratio (emax), sand is poured into a cylinder with vanishing height. As large deformations are developed during the steady state at zero pressure, a state close to critical state is reached. Furthermore, a comparison of ec0 and emax reveals good correspondence [7]. Assuming ec0 =  emax, gravity deposition simulations were carried out similar to the methodology proposed by Abbrireddy and Clayton [1]. A cuboidal space of size 0.15 m × 0.15 m × 0.45 m was filled with a randomly distributed cloud of particles with no overlap and very high initial porosity. Gravity was switched on, and the particles were free to settle in the cuboid. Once the unbalanced forces reach a stable value of 0.01, the void ratio of the settled particles was computed. Many researchers have studied the effect of the wall on the void ratio [15], and due to these boundary effects, the void ratios were computed at a distance of 2.5d50 from the edges and 5d50 from the bottom.

2.4.3 Minimum Void Ratio at Zero Pressure (ed0)

When a packing of particles is subjected to tapping or vibrations, the packing experiences densification which depends on the conditions of the vibrations applied and this forms the basis for determination of minimum void ratio in the laboratory (emin). Moreover, when cyclic shearing with small amplitude is performed after static compression, ed0 is reached asymptotically. A comparison of ed0 and emin shows that the values are usually close to each other. Therefore, ed0 is equal to emin is assumed in this study [7]. Chang et al. [4] followed the standard ASTM D4253 to simulate densification using DEM. Similar to their methodology, densification simulations with vertical vibrations were conducted to compute the ed0 values. To simplify the simulations, a cloud of particles were created in a cubical container of size 0.2 m. These particles were allowed to settle under gravity in a stable loose packing. The top plate of the container was pressed with a surcharge of 14 kPa. The bottom plate was vibrated as a sinusoidal oscillator whose amplitude was taken as 0.2 times the maximum particle size with the frequency of 60 Hz. ed0 was reported when a stable void ratio was reached asymptotically, which did not change with the time of simulation.

3 Results and Discussion

3.1 Calibration of Contact Parameters

Figure 4 shows the comparison of numerical and experimental results for triaxial tests for dense Karlsruhe sand (e  = 0.53) at different confining pressure. Both experimental curves, global axial normal stress with axial strain and volumetric strain with axial strain, were reproduced very well. The calculated friction angle from simulations is 41.4° which correlates well with the experimental value of 43.7°. Similarly, the dilatancy angle from simulations is 31.2° and is in satisfactory agreement with the experimental result of 28.5°. The calibrated micromechanical parameters obtained were: Ec = 85 GPa, ν  = 0.2, ρ  = 2660 kg/m3, μ  = 3°, β  = 0.15, η  = 0.5. For Ec = 85 GPa, approximate kn value is computed close to 0.85 GPa, which is in the range of values found in the literature. These calibrated contact parameters were used in the simulations in the subsequent simulations to compute the value of hypoplastic law parameters using simple experimental simulations.

Fig. 4
figure 4

Comparison of results from numerical and experiment results of the triaxial test on Karlsruhe Sand

Full size image

3.2 Limiting Void Ratios at Zero Pressure

Figure 5 shows the variation of void ratio with confining stress during isotropic compression from a cloud of particles in a gravity-free space. The solid black lines show the result of isotropic compression as obtained from YADE and dotted red lines shows the fit theoretical curve. Also, Fig. 5 shows the variation of void ratio with time for vertical vibrations simulation. The initial straight part is the gravity deposition process and after the particles are settled the particles are vibrated. Parameters obtained from DEM simulations and the corresponding values as given in [7] are summarized in Table 1. Even through the angularity of particles is simulated by using a rotational resistance at the contact, due to inherit sphericity of the particles, the limiting void ratios are lower in value for simulated results. In order for rotational resistance to come into the picture, the simulation has to be done in a quasi-static regime which is not the case with gravity deposition. Also, the value of hs is lower for simulation results than literature values. The value of 1450 MPa is close to the value of Hochstetten sand, Hostun RF sand, and Lausitz sand, which are predominately subrounded in shape.

Fig. 5
figure 5

a Variation of void ratio with confining stress during isotropic compression; b variation of void ratio with a time of simulation for vertical vibration test

Full size image
Table 1 Summary of hypoplastic parameters as obtained from DEM simulations and literature
Full size table

3.3 Triaxial Test Simulations

A MATLAB code was created to simulate the triaxial test using eight parameters of hypoplastic law. Using Eqs. 2 and 3, the code computes the corresponding stress-strain and volume change for every time step Fig. 6 shows the comparison of stress-strain and volume change behavior of Karlsruhe sand as obtained from experiments, DEM simulations, simulations using hypoplastic law with parameters obtained from literature and simulations using hypoplastic law with parameters obtained from DEM simulations. Only the results from hypoplastic simulations using parameters from the literature show a distinct peak state. The results from hypoplastic simulations with parameters from DEM simulations are on the lower side, yet follow the experimental results in parallel. In all the cases the DEM simulation results and simulations using hypoplastic law with parameters obtained from the literature are more dilative in comparison to other results. It is interesting to note that although the limiting void ratios from DEM simulations are lower than the values from literature, they do not change the triaxial test simulation results considerably. This is because the computation of parameters fd (Eq. 4) and fb (Eq. 5), the limiting void ratios are taken in the form of a ratio, which remains fairly constant over the range of stress. For example, the value of the ratio (ei0 − ed0)/(ec0 − ed0) for parameters in column 2 of Table 1 comes out to be 1.6, and for column 3 of Table 1 it comes out to a similar value of 1.52. The trend of similar ratio value is continued throughout the stress range. The major difference in the response of the two hypoplastic simulations comes from the different values of hs and, a higher hs value makes the overall response more dilative with a distinct peak.

Fig. 6
figure 6

Comparison of triaxial test results at confining pressure of 100 kPa (top), 200 kPa (middle) and 300 kPa (bottom)

Full size image

4 Conclusions

This paper illustrates the versatility of the Discrete Element Method in the simulation of conventional geotechnical tests, in order to understand the underlying mechanics behind the behavior of granular materials. An attempt has been made to understand the behavior of sands in macro-, micro- and continuum scale, under generalized loading conditions. The main conclusions are

  1. 1.

    Numerical simulations of a quasi-static triaxial test using DEM show good correspondence with the experimental results on Karlsruhe Sand. To complement the simplicity of hypoplastic law, a simple linear elastic normal contact with linear, rotational moment law is proposed to simulate the response of particles over upscaled grain sized distribution of Karlsruhe sand. At failure, a clear slip plane is observed for a sample with an aspect ratio of 3 (Fig. 2).

  2. 2.

    Limiting void ratios for the hypoplastic law parameters were computed using various DEM simulations (ei0 using isotropic compression, ec0 using gravity deposition, ed0 using vertical vibrations) and compared to the values reported in the literature. Although rotational law was used to simulate the angularity of the particles, limiting void ratios for DEM simulations were lower than the ones reported in the literature.

  3. 3.

    MATLAB code was created to simulate the triaxial test using hypoplastic constitutive law. The results of experimental triaxial tests on Karlsruhe Sand were fairly well produced by triaxial test simulation using hypoplastic law with parameters obtained from the literature, as well as, DEM simulations of simple geotechnical tests. As the limiting void ratios are computed as ratios in Eqs. 4 and 5, the effect of the difference between experimental and simulated limiting void ratio on the results of triaxial test simulations using hypoplasticity appears to be inconsequential. The difference could be attributed to the value of peak friction angle, critical friction angle, and parameter (hs). A parametric study is required to understand the effect of different parameters on the result of triaxial simulations with hypoplastic.

With this paper, we take one step forward in the formulation of a unified theory which can help us understand the behavior of soils using experiments, micro-scale dis-continuum DEM simulations and continuum-based constitutive laws.