Keywords

1 Introduction

The bearing capacity of shallow foundation is generally estimated by considering soil as a homogeneous medium. However, the natural soil deposits are generally stratified. One of the earliest work to estimate the bearing capacity of two-layered clay deposit was carried out by Reddy and Srinivasan [1] by using limit equilibrium method and assuming circular failure mechanism. Based on the experimental results, Brown and Meyerhof [2] proposed empirical equations to calculate the bearing capacity of two layered clay for circular and strip foundation. Chen [3] addressed the layered problem by employing the upper bound limit analysis and adopting the circular failure mechanism. Meyerhof and Hanna [4] proposed the semi-empirical formulae for estimating the bearing capacity of strip and circular foundation resting over strong layer overlaying weak deposit and weak layer over strong deposits. A punching shear failure mechanism was suggested for the case of strong layer overlying weak deposits. For the case of weak layer overlaying strong deposits, the failure was assumed by squeezing of the top weak layer. By using slip surface method, Georgiadis and Michalopoulos [5] presented bearing capacity of strip foundation for any combination of cohesive and cohesionless soil. Merifield et al. [6] bracketed the bearing capacity of strip foundation resting on two layered clayey soil by using linear approximation of Tresca yield criterion. Michalowski [7] presented the upper bound solution for strip foundation placed on two-layered clay subjected to both horizontal and vertical loads. Kuo et al. [8] predicted the bearing capacity of strip foundation on multilayer clayey soil by adopting ANN-based model. Benmebarek et al. [9] and later. Ahmadi et al. [10] used explicit finite difference code FLAC estimate the bearing capacity of strip foundation placed on two-layered clay soil.

From the available literature, it is evident that most of the studies on layered clays have been carried out for strip foundations and the available rigorous solutions for the strip foundations are based on linearization of the yield criterion. However, there are very few literatures available for determining the bearing capacity of circular foundations. In the present study, an attempt is made to estimate the rigorous bearing capacity of strip and circular foundation resting on two-layered clays by using the lower and upper bound limit analysis in conjunction with finite elements and nonlinear optimization. The advantage of finite-element limit analysis is that it does not require any assumption regarding the size and shape of the failure surface and the failure mechanism. The bearing capacity for strip and circular foundation are presented for different ratios of t/b and cu1/cu2. The obtained solutions are further compared with the available data from the literature.

2 Problem Domain, Boundary Conditions, and Statement of the Problem

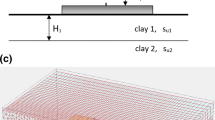
A rough circular footing of diameter b (for strip footing, b equals to width of the footing) is rested over two layered clays; where, the undrained cohesive strength of the top (of thickness t) and the bottom layers are cu1 and cu2 respectively. The bearing capacity of strip and circular foundation are calculated by assuming the problem to be of plane strain case and axisymmetric case, respectively. In the present analysis, full domain is being adopted for the plane strain case. However, due to its symmetricity and two-dimensional nature of the axisymmetric problem, only half of the domain is considered in the analysis. The boundary conditions of the plane strain and the axisymmetric case are depicted in Fig. 1.

Fig. 1
figure 1

Problem Domain and boundary conditions for a circular foundation, and b strip foundation

Full size image

The length and the depth of the domain are chosen to be sufficiently large so that the failure zone is confined well within the domain; the magnitude of L and D for strip and circular footing are considered to be 7.5 b. Both the clay layers are assumed to be perfectly plastic and governed by the Mohr–Coulomb yield criterion and associated flow rule. It is intended to calculate the bearing capacity of the foundation for different ratios of t/b and cu1/cu2.

3 Methodology

The numerical limit theorems are applied here for obtaining the limiting solutions. In order to obtain the lower bound solution a statically admissible stress field is required to construct in the domain. On the contrary, a kinematically admissible velocity field is required to perform the upper bound analysis. The detailed methodology of obtaining the limiting solutions for plane strain problems using linear/nonlinear optimization can be referred in the work of Sloan [11], Sloan and Kleeman [12], Makrodimopoulos and Martin [13, 14], Chakraborty and Kumar [15]. The basis of obtaining both the extremities for axisymmetric problems can be viewed in the article of Kumar and Khatri [16], Kumar and Chakraborty [17].

In the present article, the lower and upper bound limit analysis has been performed using Optum G2 [18] along with adaptive mesh refinement based on plastic shear dissipation. Mesh refinement based on shear dissipation is considered most efficient and reliable for limit analysis. The clay in both the layer is assumed to isotropic, undrained and completely saturated. It can be noted that for undrained and completely saturated case (i.e., ϕ = 0°) Mohr–Coulomb yield criterion eventually becomes the Tresca criterion.

4 Results

4.1 Numerical Solutions

The bearing capacity (qu) for strip and circular footing is obtained by lower (LB) and upper bound (UB) limit analysis. The difference between the LB and UB solutions remains negligible in most of the cases. The actual collapse load is supposed to be within these two extreme values. The solutions are presented as the non-dimensional form of the bearing capacity, namely, qu/cu2. Figures 2 and 3 depict the variation of qu/cu2 with t/b corresponding to different values of cu1/cu2 ratio. The bearing capacities are presented as the average of the LB and UB solutions.

Fig. 2
figure 2

Variation of non-dimensional bearing capacity (qu/cu2) for stiff layer overlaying soft layer (cu1/cu2> 1) for a circular foundation, and b strip foundation

Full size image
Fig. 3
figure 3

Variation of non-dimensional bearing capacity (qu/cu2) for soft layer overlaying stiff layer (cu1/cu2 < 1) for a circular foundation, and b strip foundation

Full size image

Figure 2 represents the bearing capacity for the case where the footings are placed over stiff clay overlying soft clay (Case A) and Fig. 3 represents the bearing capacity for the footings placed over soft clay overlying stiff clay (Case B). It is observed that the bearing capacity depends upon (i) t/b ratio, (ii) cu1/cu2 ratio and (iii) the type of foundation. In this analysis, the ratio of cu1/cu2 was varied between 0.1 and 10. This range is sufficient to cover almost all practical cases. From the results of Meyerhof and Hanna [4] and Merifield et al. [6] it can be inferred that when (i) t/b < 0.125, the top layer does not have appreciable influence on qu and (ii) t/b > 2, the bearing capacity of circular/strip footing depends only on the top layer. Hence, the range of t/b, correspond to a certain cu1/cu2 ratio, is kept between 0.125 and 3.

For Case A, the magnitude of the bearing capacity increases with increase in t/b and cu1/cu2 ratio. Figure 2 shows that for a specific cu1/cu2 ratio, the increment of the bearing capacity takes place up to a certain value of t/b; beyond this particular value of t/b there is no further improvement in strength prediction. For Case B, the graph shows completely opposite trend. The value of qu/cu2 decreases with increase in t/b. The rate of decrement is significantly higher for smaller t/b. After a certain value of t/b, the graph attains a constant value. In this text, the particular value of t/b beyond which there is no appreciable change of bearing capacity is denoted as topt/b (i.e., optimum t/b). This can be interpreted as that the bearing capacity is solely governed by the strength characteristics of the top layer (cu1) when t/b is greater than topt/b. The magnitude of topt/b depends on cu1/cu2 ratio and the type of the foundation.

Figure 4 presents the variation of topt/b with different values of cu1/cu2 ratio. It is observed that as long as cu1/cu2 is smaller than 1, the magnitude of topt/b remains to be constant. On the contrary, for Case A, topt/b increases continuously with increase in cu1/cu2; however, the rate of increment reduces with higher cu1/cu2 value.

Fig. 4
figure 4

Variation of topt/b with cu1/cu2 for the circular and strip foundation

Full size image

Figure 2 also suggests that for a specific t/b and cu1/cu2 ratio, the bearing capacity of circular foundation is greater than that of its strip counterpart. The difference between the bearing capacity increases with increase in cu1/cu2. It is quite evident from Fig. 4 that for the same cu1/cu2, the topt/b value for circular foundation is quite smaller as compared to that of strip foundation.

4.2 Failure Patterns

Lower bound solutions are used to obtain the failure patterns for several cases. For the strip footing, the state of stress at any point is being specified by (i) σx, σy and τxy for the strip footing, and, (ii) σr, σz, τrz and σθ for the circular footing. After obtaining the stresses at each node, the ratio of a/d is calculated; where, a represent the radius of Mohr circle defining the state of stress at the node and d represents the radius of Mohr circle touching the failure envelope. On the basis of a/d ratio the failure patterns are drawn. As a/d approaches 1, plastic shear failure of the soil will take place and if a/d < 1 the state of soil will be in a non-plastic state. The detailed procedure of calculating a and d for circular footing can be seen in the work of Kumar and Chakraborty [19].

Figures 5 and 6 depict the failure pattern for strip and circular foundation corresponding to Case A and Case B, respectively. The figures were drawn for different t/b ratio corresponding to a specific cu1/cu2 ratio. The dark patch in the figures indicates the failure zone. For the sake of clarity half of the failure domain beneath the strip foundation is shown in the present article. From Fig. 5, it is observed that the horizontal and the vertical extent of the failure zone gets further extended with the increase of t/b value. The extension of the plastic zone continues up to topt/b; beyond that the failure zone decreases and remains confined only to the top layer. The failure pattern also suggests that for the same type of strata, strip footing yields larger failure zone than the circular footing. Comparing Figs. 5 and 6, it can be concluded that the expansion of the failure zone for Case A is far higher than that of Case B. This is observed for both the strip as well as circular footing. From the failure pattern a non-plastic triangular wedge is observed below the foundation. The size of the wedge reduces with the increase of t/b ratio. A second non-plastic wedge is also observed adjacent to the strip footing, as mentioned by Merifield et al. [6]. This adjacent wedge increases in size with the increase in t/b ratio.

Fig. 5
figure 5

For cu1/cu2= 2, the failure patterns for a strip foundation with t/b equals to a 0.125, b 1, and c 2 and for a circular foundation with t/b equals to d 0.125, e 1, and f 2

Full size image
Fig. 6
figure 6

For cu1/cu2= 0.5, the failure patterns for a strip foundation with t/b equals to a 0.375, and b 1.5, and for a circular foundation with t/b equals to c 0.375, and d 1

Full size image

4.3 Nodal Velocities

Velocity contours are plotted from the results of upper bound analysis. The nodal velocity diagrams illustrate the magnitudes and the directions of the soil movement at various points within the considered domain. Figures 7 and 8 present nodal velocity pattern for strip and circular foundation corresponding to two different cu1/cu2 ratios, namely, 3 and 0.5. It can be clearly observed that the velocities of the soil particles along the ground surface and adjacent to the footing edge are significantly higher as compared to the velocities of the soil particles just beneath the footing edge. The formation of the triangular rigid wedge beneath the footing replicates the similar outcome as observed in the failure contour drawn by using the lower bound stress field solution. The velocity discontinuities are found to be prominent near the footing edge. The zone of influence which indicates the soil portion where the velocities are significantly higher than the rest of the domain depends highly on cu1/cu2, t/b, and, the type of foundation. It is clearly observed that compare to the strip foundation the extent of the zone of influence is lesser for the case of circular foundation.

Fig. 7
figure 7

For cu1/cu2= 3, the nodal velocity contours for a strip foundation with t/b equals to a 0.125, b 1.75, and c 2 and for a circular foundation with t/b equals to d 0.125, e 1, and f 2

Full size image
Fig. 8
figure 8

For cu1/cu2= 0.5, the nodal velocity contours for a strip foundation with t/b equals to a 0.125, b 0.75, and c 1.5 and for a circular foundation with t/b equals to d 0.125, e 0.375, and f 1.5

Full size image

5 Comparison of Results

Table 1 presents the comparison of the obtained limiting solutions for the strip footings with the available solutions in the literature. The present solutions are validated on the basis of bearing capacity factor, N*c, where N*c = qu/cu1. The comparisons are provided for Case A as well as Case B. The LB and the UB solutions remain closer to each other. The comparisons show that the UB and LB solutions obtained from the present analysis lie between the limiting values presented by Merifield et al. [6]. The LB and UB solutions obtained by Merifield et al. [6] were within a 12% bracket of the average collapse load whereas the current solutions lie within a 2% bracket of the average solution. The reason of this improvement can be attributed to the fact that unlike the liner optimization employed by Merifield et al. [6], the present analysis is performed by second order conic optimization. The present solutions are also compared with the semi-analytical solutions of Meyerhof and Hanna [4], numerical solutions of Michalowski [7] and Ahmadi et al. [10]. The present solutions compare quite well with the available solutions. Table 2 shows the comparison for the circular footings with the available semi-analytical solutions of Meyerhof and Hanna [4]. The obtained limiting solutions are higher than the values provided by Meyerhof and Hanna [4] for Case A. However, for Case B, the bearing capacity factor presented by Meyerhof and Hanna [4] are on the higher side. This trend is being observed for both the strip and circular footing. The difference between the present and the semi-analytical solutions are noticeable as long as t/b < topt/b. The present solutions are also verified with the results of experimental model test performed by Meyerhof and Hanna [4] and are displayed in Table 3. The average value of LB and UB solution agrees quite well with the experimental observations.

Table 1 Value of bearing capacity factor (N*)c for strip foundation
Full size table
Table 2 Value of bearing capacity factor (N*c) for circular foundation
Full size table
Table 3 Comparison with experimental result for cu1/cu2= 3.5
Full size table

The optimum t/b ratio for both circular and strip foundation obtained from the solution of Meyerhof and Hanna [4] are higher as compared to the optimum t/b ratio of the present solution.

6 Conclusion

In this article, the bearing capacity for strip and circular footing resting on two layered clay medium has been estimated by using numerical limit theorems in conjunction with finite elements and second order cone optimization. The strength predictions were carried out by varying the (i) undrained shear strength of the two layers (represented as non-dimensional form, namely, cu1/cu2) and (ii) top layer thickness (represented as t/b ratio). The design charts are provided by averaging out the lower and upper bound solutions. There always remains a certain top layer thickness (topt) beyond which there is no impact of the bottom layer strength value. The value of topt/b varies with the type of foundation and cu1/cu2 ratio. The failure contours and the nodal velocity patterns further present clearly the extent of the failure zone and the magnitude and the direction of the movement of the soil particles in the zone of influence. The results from the analysis were found to match reasonably well with the available analytical, numerical, and experimental solutions from the literature.