Keywords

1 Introduction

Optimal Reactive Power Dispatch (ORPD) is the subcategory of Optimal Power Flow (OPF) optimization framework. In the ORPD, redistribution of reactive power sources (such as the magnitude of the voltage of the generators, transformer’s tap position, and value of VAR compensation devices) has been used to reduce total active power losses and total voltage deviation. In literature, many solution methodologies for the ORPD problem have been already proposed and analyzed their performances by various researchers. These solution methodologies may be classified into two broad categories: (a) classical methodologies, and (b) intelligent metaheuristic methodologies [1]. The classical methods are appropriate for single modal optimization problems with decent convergence capabilities. The main drawback of the classical methods is that they are unable to handle the multimodal optimization problems [1]. Whereas, the intelligent metaheuristic optimization methods may be applied to solve the multimodal optimization problems.

The intelligent metaheuristic methodologies may be listed as: Particle Swarm Optimization (PSO) [2], Cataclysmic Genetic Algorithm (CGA) [3], Self-Adaptive Real-Coded Genetic Algorithm (SA-RCGA) [4], Principal Component Analysis (PCA) based Real Coded GA [5], Differential Evolutionary Algorithm (DEA) [6,7,8], Seeker Optimization Algorithm (SOA) [9], Harmony Search Algorithm (HSA) [10], Biogeography-Based Optimization (BBO) [11], Ant Colony Optimization (ACO) [12], Teaching Learning-Based Optimization (TLBO) and Quasi-Oppositional Teaching Learning-Based Optimization (QOTLBO) [13], PSO with scale-free Gaussian-dynamic [14], etc. Similarly, the hybrid form of these metaheuristic methodologies may be listed as real coded GA and Simulated Annealing (SA) [15], the Multi-Agent System (MAS) and PSO [16], the modified PSO (GA into PSO) and MAS [17], Shuffled Frog Leaping Algorithm (SFLA) and Nelder–Mead (NM) [18], Modified Imperialist Competitive Algorithm (MICA) and Inverse Weed Optimization Algorithm (IWOA) [19], Modified TLBO and Double Differential Evolution (DDE) [20], PSO and Gravitational Search Algorithms (GSA) [21], etc.

In this paper, the interface between MATLAB and DigSILENT PowerFactory software has been used to solve the optimal reactive power dispatch problem [22]. The power flow calculations have been executed on DigSILENT PowerFactory software, whereas the process of optimization through Genetic Algorithm has been implemented on MATLAB. The proposed approach has been tested on standard IEEE 30 bus system. The results obtained by the proposed approach has been compared with the results presented in the literature [21]. Rest of the paper has been organized as follows: the complete mathematical formulation of ORPD problem has been presented in Sect. 2. The flowchart of the proposed approach is presented in Sect. 3. The results obtained from the proposed approach are presented in Sect. 4. Finally, the conclusion of the paper is presented in Sect. 5.

2 Problem Formulation

The primary purpose of the ORPD problem is to reduce the total active power losses in the transmission lines and to improve the voltage profile of load buses. The complete mathematical formulation for ORPD is presented below.

2.1 Objective Function

$$ P_{\text{loss}} = \mathop \sum \limits_{k = 1}^{{N_{TL} }} g_{k} \left[ {V_{i}^{2} + V_{j}^{2} - 2V_{i} V_{j} \cos \left( {\delta_{i} - \delta_{j} } \right)} \right] , \forall \,i \in N_{\text{Bus}} ,\forall \,j \in N_{\text{Bus}} $$
(1)
$$ VD = \mathop \sum \limits_{k = 1}^{{N_{\text{Bus}} }} \left| {V_{k} - V_{k}^{sp} } \right| $$
(2)

2.2 System Constraints

$$ P_{{G_{i} }} - P_{{D_{i} }} = V_{i} \mathop \sum \limits_{j = 1}^{{N_{\text{Bus}} }} \left[ {G_{ij} \cos \left( {\delta_{i} - \delta_{j} } \right) + B_{ij} \sin \left( {\delta_{i} - \delta_{j} } \right)} \right] ,\quad \forall \,i,j \in N_{\text{Bus}} $$
(3)
$$ Q_{{G_{i} }} - Q_{{D_{i} }} = V_{i} \mathop \sum \limits_{j = 1}^{NB} \left[ {G_{ij} \cos \left( {\delta_{i} - \delta_{j} } \right) - B_{ij} \sin \left( {\delta_{i} - \delta_{j} } \right)} \right] ,\quad \forall \,i,j \in N_{\text{Bus}} $$
(4)
$$ V_{{G_{i} }}^{ \hbox{min} } \le V_{{G_{i} }} \le V_{{G_{i} }}^{ \hbox{max} } \,\forall \,i \in N_{\text{Gen}} $$
(5)
$$ P_{{G_{i} }}^{ \hbox{min} } \le P_{{G_{i} }} \le P_{{G_{i} }}^{ \hbox{max} } \,\forall \,i \in N_{\text{Gen}} $$
(6)
$$ Q_{{G_{i} }}^{ \hbox{min} } \le Q_{{G_{i} }} \le Q_{{G_{i} }}^{ \hbox{max} } \,\forall \,i \in N_{\text{Gen}} $$
(7)
$$ T_{j}^{ \hbox{min} } \le T_{j} \le T_{j}^{ \hbox{max} } \,\forall \,j \in N_{\text{Tap}} $$
(8)
$$ Q_{{C_{i} }}^{ \hbox{min} } \le Q_{{C_{i} }} \le Q_{{C_{i} }}^{ \hbox{max} } \,\forall \,i \in N_{\text{Cap}} $$
(9)
$$ V_{{L_{i} }}^{ \hbox{min} } \le V_{{L_{i} }} \le V_{{L_{i} }}^{ \hbox{max} } \,\forall \,i \in N_{PQ} $$
(10)
$$ S_{j} \le S_{j}^{ \hbox{max} } \,\forall \,j \in N_{\text{Tline}} $$
(11)
$$ x^{T} = \left[ {V_{{G_{1} }} \ldots V_{{G_{{N_{\text{Gen}} }} }} ,Q_{{C_{1} }} \ldots Q_{{C_{{N_{\text{Cap}} }} }} ,T_{1} \ldots T_{{N_{\text{Tap}} }} } \right] $$
(12)
$$ u^{T} = \left[ {P_{{G_{1} }} ,V_{{L_{1} }} \ldots V_{{L_{{N_{PQ} }} }} ,Q_{{G_{1} }} \ldots Q_{{G_{{N_{\text{Gen}} }} }} } \right] $$
(13)

2.3 General Formulation of the Objective Function

The final objective function, which is used by the optimization algorithm as given below.

$$ {\text{minimize}}\,F = F_{OBF} + PN_{1} \alpha_{{PN_{1} }} + PN_{2} \alpha_{{PN_{2} }} + PN_{3} \alpha_{{PN_{3} }} $$
(14)
$$ PN_{1} = \left( {P_{{G_{1} }} - P_{{G_{1} }}^{ \lim } } \right)^{2} ,\quad \alpha_{{PN_{1} }} = \left( {PN_{1} + 1} \right) $$
(15)
$$ PN_{2} = \mathop \sum \limits_{i = 1}^{NL} \left( {V_{{L_{i} }} - V_{{L_{i} }}^{ \lim } } \right)^{2} ,\quad \alpha_{{PN_{2} }} = \left( {PN_{2} + 1} \right) $$
(16)
$$ PN_{3} = \mathop \sum \limits_{i = 1}^{NG} \left( {Q_{{G_{i} }} - Q_{{G_{i} }}^{ \lim } } \right)^{2} ,\quad \alpha_{{PN_{3} }} = \left( {PN_{3} + 1} \right) $$
(17)

3 Solution Methodology

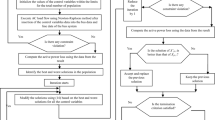
The flow chart of the proposed approach has been presented in Fig. 1. In this paper, two modification has been proposed: one is “MIN MAX modification” and second is “Violation of the Constraints Penalize by itself”. In MIN MAX modification, the minimum value of the control variables are set as the “base value” and the difference between the upper and lower boundary of the control variables are set as the “difference value”. Now, the new setting of the upper and lower limit of the control variables are “1” and “0”, respectively. GA performs optimization process using newly defined range of control variables.

Fig. 1
figure 1

Flowchart of the interface between GA and DigSILENT PowerFactory

Full size image

In second modification, violations of control variables as depicted in Eq. (12) have restricted by the lower and upper limit of the control variables. Similarly, violation of the state variables as depicted in Eq. (13) have been restricted by penalty based objective function as depicted in Eq. (14). Penalty function approach has been used to handle the violation of the inequality constraint [5]. The violation of the constraints has been penalized by the proposed penalty factor. The formulation of the proposed penalty factors is presented in Eqs. (15–17). \( PN_{1} \), \( PN_{2} \) and \( PN_{3} \) are the measurement of the violation of the state variables and \( \alpha_{{PN_{1} }} \), \( \alpha_{{PN_{2} }} \) and \( \alpha_{{PN_{3} }} \) are the penalty factor, respectively.

4 Simulation Result

In this section, the proposed approach has been tested on standard IEEE 30 bus system. The IEEE 30 bus system data and limits of control and state variables are adapted from [21]. The total active power demand of the system is 2.834 p.u. at 100 MVA base. In this paper, 30 individual test runs have performed to validate the proposed approach. Results obtained by the proposed approach have been compared with those reported in [21]. The target objectives, those are presented by Eq. (1) (case 1) and Eq. (2) (case 2) and formulated as Eq. (14), have been solved using the proposed approach. The comparison of the results obtained by proposed approach and results reported in [21] are presented in Tables 1 and 2. The convergence graph of the target objectives is depicted in Fig. 2.

Table 1 Comparison of results for case 1
Full size table
Table 2 Comparison of result for case 2
Full size table
Fig. 2
figure 2

Convergence of the total active power loss (a) and voltage deviation (b) in IEEE 30 bus power system using the proposed optimization method

Full size image

It is observed from the Table 1 that the proposed approach is able to reduce the total active power losses in the transmission line 4.5323 MW that is 22.16% from the initial value 5.8223 MW in comparison to 22.04% with PSO [21], 21.83% with GSA [21]. Also, it is observed from the Table 2 that the proposed approach is able to reduce the total voltage deviation 0.1002 pu that is 91.29% from the initial value 1.1497 pu in comparison to 91.26% with PSO [21], 88.77% with GSA [21]. The statistical analysis in terms of Best, Worst and Standard Deviation (SD) for Case 1 (i.e. power loss minimization) and Case 2 (i.e. voltage deviation minimization) are listed in Tables 3 and 4, respectively.

Table 3 Comparison of best, worst, and standard deviation (SD) for case 1
Full size table
Table 4 Comparison of best, worst, and standard deviation (SD) for case 2
Full size table

5 Conclusion

In this paper, the ORPD problem has been successfully solved by the proposed GA based optimization approach. ORPD is a nonlinear, nonconvex, non differentiable, and multimodal problem with a discrete and continuous control variable. In this study, two different objective functions such as total active power loss in the transmission line and total voltage deviation on load buses have been minimized subjective to different equality and inequality constraints for IEEE 30 bus power system. In addition, the interface between GA and DigSILENT PowerFactory software has been realized efficiently to solve the ORPD problem. The obtained results demonstrate the potential and effectiveness of the proposed approach.