Keywords

1 Introduction

As the electric vehicle and in-wheel motor technology develops rapidly, a four in-wheel-motor independent-drive electric vehicle (4MIDEV) has attracted lots of attention [1, 2]. Compared with the traditional vehicle, the 4MIDEV is directly driven by four motors integrated into wheel hubs without the need for additional mechanical transmission components, such as drive shafts. Since the torque of each drive wheel can be independently controlled, this distributed drive form brings more possibilities for achieving better stability and maneuverability of the vehicle [3]. In recent years, a great deal of valuable work has been carried out on the steering stability control of the 4MIDEV.

The stability control strategy of the 4MIDEV generally adopts a hierarchical structure, including an upper control level to compute the virtual force commands and a lower control level to realize the control of each wheel torque [4]. However, the previously proposed control strategy rarely considers the effects of changes in the adhesion coefficient, which may introduce additional control errors. As the road conditions become more complex, there is a need for a new stability control strategy adapted to road adhesion, so as to ensure good steering stability control effect. Thus, the requirements for the upper control level and the lower control level are much higher.

The direct yaw moment control (DYC) has been widely used in the upper control level and proved to be very effective [4,5,6]. Most of the DYCs proposed so far only control the yaw rate without the consideration of the sideslip angle [7] or take the sideslip angle as an intermediate variable in the control of the yaw rate [8, 9]. Although accurate control of the yaw rate can be achieved, these methods have poor consideration of the sideslip angle or require a high accuracy for estimating the sideslip angle [2]. Furthermore, the impact of adhesion coefficient is seldom taken into account in the DYC, which will greatly affect the final stability control results when the adhesion coefficient changes. In the lower control level, the optimal torque allocation algorithm is preferred over other algorithms such as average allocation and dynamic-load allocation [10, 11], whose optimal objective usually selects the tire workload usages to reflect steering stability [1, 12]. However, the different adhesion conditions at each wheel are always neglected in the torque allocation. The tire workload usages are generally considered to be equally important for stability, i.e., their weight coefficients were equal or independent of the adhesion coefficient, which may result in extreme loads on the wheels at low adhesion while other wheels still have a relatively high stability margin.

To solve the above problems, this paper proposes an adaptive stability control strategy to accommodate different adhesion coefficients. The proposed strategy adopts a hierarchical structure which takes the road adhesion coefficient into account in both the upper control level and lower control level. The adaptive control of the yaw rate and the sideslip angle is realized in the upper control level to ensure a better DYC control result. A weight-based optimal torque allocation algorithm is also developed in the lower control level to achieve different weight control of each motor torque according to road adhesion coefficient. The adaptive upper control level and the lower control level can effectively improve the steering stability of the 4MIDEV under different road adhesion coefficients.

2 Design of Adaptive Steering Stability Control Strategy for the 4MIDEV

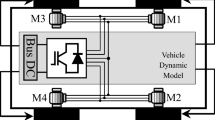
The proposed adaptive stability control strategy, as shown in Fig. 1, consists of a reference output level with reference dynamic model, an upper control level based on the yaw moment control and speed control, and a lower control level with the weight-based optimal allocation algorithm.

Fig. 1
figure 1

Configuration of adaptive stability control strategy

Full size image

2.1 Reference Output Level

The reference output level adopts a reference model to compute the desired dynamics parameters, such as the sideslip angle and the yaw rate, for the further control of the upper control level. To investigate the planar motion of the vehicle, a three-degree-of-freedom (3-DOF) model is constructed by ignoring the roll and pitch motions, as shown in Fig. 2, which can be described as:

Fig. 2
figure 2

Vehicle dynamics model

Full size image
$$\left[ {\begin{array}{*{20}c} {\dot{V}_{x} } \\ {\dot{V}_{y} } \\ {\dot{\gamma }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {V_{y} \gamma - \frac{{\rho C_{d} }}{2m}AV_{x}^{2} } \hfill \\ { - V_{x} \gamma } \hfill \\ 0 \hfill \\ \end{array} } \right] + {\mathbf{B}}_{x} \left[ {\begin{array}{*{20}c} {F_{xfl} } \\ {F_{xfr} } \\ {F_{xrl} } \\ {F_{xrr} } \\ \end{array} } \right] + {\mathbf{B}}_{{\mathbf{y}}} \left[ {\begin{array}{*{20}c} {F_{yfl} } \\ {F_{yfr} } \\ {F_{yrl} } \\ {F_{yrr} } \\ \end{array} } \right]$$
(1)

where \(V_{x}\) and \(V_{y}\) denote the longitudinal velocity and the lateral velocity of vehicle, respectively, and \(\dot{V}_{x}\) and \(\dot{V}_{y}\) are their derivatives. \(\gamma\) and \(\dot{\gamma }\) denote the yaw rate and its derivative, respectively. \(\rho\) denotes the air density, \(C_{d}\) is the air resistance coefficient, and A represents the maximum cross-sectional area. m stands for the mass of vehicle. \(F_{xij}\) and \(F_{yij}\) are the longitudinal and lateral forces of the wheels, respectively. \(i \in \{ f,r\}\) stands for the front or the rear and \(j \in \{ l,r\}\) stands for the left or the right.

The coefficient matrices \({\mathbf{B}}_{x}\) and \({\mathbf{B}}_{y}\) can be formulated as:

$${\mathbf{B}}_{x} = \left[ {\begin{array}{*{20}c} {\frac{{\cos \delta_{f} }}{m}} & {\frac{{\cos \delta_{f} }}{m}} & {\frac{1}{m}} & {\frac{1}{m}} \\ {\frac{{\sin \delta_{f} }}{m}} & {\frac{{\sin \delta_{f} }}{m}} & 0 & 0 \\ {\frac{{a\sin \delta_{f} - d\cos \delta_{{_{f} }} }}{{I_{z} }}} & {\frac{{a\sin \delta_{f} + d\cos \delta_{f} }}{{I_{z} }}} & { - \frac{d}{{I_{z} }}} & {\frac{d}{{I_{z} }}} \\ \end{array} } \right]$$
(2)
$${\mathbf{B}}_{y} = \left[ {\begin{array}{*{20}c} { - \frac{{\sin \delta_{f} }}{m}} & { - \frac{{\sin \delta_{{_{f} }} }}{m}} & 0 & 0 \\ {\frac{{\cos \delta_{{_{f} }} }}{m}} & {\frac{{\cos \delta_{{_{f} }} }}{m}} & {\frac{1}{m}} & {\frac{1}{m}} \\ {\frac{{a\cos \delta_{{_{f} }} + d\sin \delta_{f} }}{{I_{z} }}} & {\frac{{a\cos \delta_{f} - d\sin \delta_{{_{f} }} }}{{I_{z} }}} & { - \frac{b}{{I_{z} }}} & {\frac{b}{{I_{z} }}} \\ \end{array} } \right]$$
(3)

where \(I_{z}\) denotes the yaw inertia of the vehicle, and \(\delta_{f}\) is the front-wheel steering angle. d is half of the tread. a is the distance between the center of gravity and the front axle, and b is the distance to the rear axle.

To more clearly and directly reflect the driver’s steering intention, the above vehicle dynamics model is simplified to two degrees of freedom, i.e., the later motion and yaw motion, as shown in Fig. 2. The target values of sideslip angle and yaw rate can be obtained from the 2-DOF model:

$$\left\{ \begin{aligned} {\gamma^{\prime}} & = \frac{1}{{1 + AV_{x}^{2} }} \cdot \frac{{V_{x} }}{l} \cdot \delta _{f} \\ {\beta^{\prime}} & = \frac{{1 - \left( {\frac{m}{L}} \right)\left( {\frac{a}{{bK_{r} }}} \right)V_{x}^{2} }}{{1 + AV_{x}^{2} }} \cdot \frac{b}{l} \cdot \delta _{f} \\ \end{aligned} \right.$$
(4)

where \(A = \frac{m}{{l^{2} }} \cdot \frac{{aK_{f} - bK_{r} }}{{K_{f} K_{r} }}\), \(K_{f}\) and \(K_{r}\) stand for the sum of the tire cornering stiffnesses of the front axle and the rear axle, respectively.

Considering the different road adhesion conditions, it is necessary to limit the above target values [2]:

$$\left\{ {\begin{array}{*{20}l} {\gamma_{\text{limit}} = \frac{0.85}{{V_{x} }}\;\upmu {\text{g}}} \hfill \\ {\beta_{\text{limit}} = \tan^{ - 1} \left( {0.02\;\upmu {\text{g}}} \right)} \hfill \\ \end{array} } \right.$$
(5)

In summary, the desired yaw rate \(\gamma_{{ - {\text{des}}}}\) and sideslip angle \(\beta_{{ - {\text{des}}}}\) can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {\gamma_{{ - {\text{des}}}} = \hbox{min} \left\{ {\left| {\gamma^{\prime}} \right|,\gamma_{\lim } } \right\} \cdot {\text{sgn}}(\delta_{f} )} \hfill \\ {\beta_{{ - {\text{des}}}} = \hbox{min} \left\{ {\left| {\beta^{\prime}} \right|,\beta_{\lim } } \right\} \cdot {\text{sgn}}(\delta_{f} )} \hfill \\ \end{array} } \right.$$
(6)

2.2 Upper Control Level

The upper control level consists of speed control and yaw moment control, as shown in Fig. 1, which computes the virtual commands of traction force and yaw moment to control the longitudinal and lateral motions of the vehicle based on the desired dynamics parameters form the reference output level.

2.2.1 Speed Control

In order to reduce the calculation cost and ensure the real-time performance, the speed control, as shown in Fig. 1, adopts the PID method to control the longitudinal traction force \(F_{{x - {\text{des}}}}\) of the vehicle according to the error between the actual speed \(V_{x}\) and the desired speed \(V_{{x - {\text{des}}}}\) from the “preview-follow” driver model [13], so as to meet the driving demand for speed. The speed \(V_{x}\) can be estimated by the driver’s input to the acceleration/brake pedal [14].

2.2.2 Yaw Moment Control

The yaw moment control selects both the yaw rate and the sideslip angle corresponding to maneuverability and stability as control variables, as shown in Fig. 1, which control the lateral motion of vehicle through a yaw moment. Unlike the yaw rate, the sideslip angle and the yaw moment are related by the nonlinear tire forces, and the estimation accuracy of the sideslip angle is limited. Thus, the influence of the sideslip angle is considered in the control of the yaw rate by introducing a correction coefficient K. Then, the nominal yaw rate \(\gamma_{0}\) can be obtained:

$$\gamma_{0} = K\gamma$$
(7)

The correction coefficient K is studied by a fuzzy controller, as shown in Fig. 1. Considering the influence of sideslip angle rate \(\dot{\beta }\), the integrated control quantity \(\beta + B_{1} \dot{\beta }\) is designed as the input of the fuzzy controller based on the \(\beta - {\text{Method}}\) theory [15] and the phase plane method [16], where \(B_{1}\) is a coefficient related to the adhesion coefficient. Furthermore, since the impact of the sideslip angle is different for the stability under different adhesion coefficients, the adhesion coefficient \(\mu\) is also introduced as the other input of the fuzzy controller. The fuzzy rules for the correction coefficient K are shown in Table 1, where seven fuzzy subsets are designed to define the values of both inputs and outputs, such as Zero (Z), Positive-Small (PS), Positive-Medium (PM), Positive-Big (PB), Negative-Small (NS), Negative-Medium (NM), and Negative-Big (NB).

Table 1 Fuzzy rules for coefficient K
Full size table

In order to adapt to the nonlinear system and minimize the calculation cost, the fuzzy PID method is adopted in the yaw moment control to make the nominal yaw rate \(\gamma_{0}\) follow the desired value \(\gamma_{{ - {\text{des}}}}\), as shown in Fig. 1. The inputs of the fuzzy PID controller are the error between the \(\gamma_{0}\) and \(\gamma_{{ - {\text{des}}}}\) and its rate. The output is the desired yaw moment \(M_{{z - {\text{des}}}}\). The fuzzy rules of the fuzzy PID controller are shown in Table 2, where \(\Delta k_{p}\), \(\Delta k_{i}\) and \(\Delta k_{d}\) are the correcting values of the proportional, integral, and differential coefficients, respectively.

Table 2 Fuzzy rules for yam moment control
Full size table

2.3 Lower Control Level

The lower control level converts the desired yaw moment and traction force from the upper control level to the driving/brake torque required for in-wheel motors based on the torque allocation algorithm. The relationship between the lower level and upper level can be summarized as:

$${\mathbf{v}} = {\mathbf{Bu}}$$
(8)

where \({\mathbf{u}} = [T_{fl} \;T_{fr} \;T_{rl} \;T_{rr} ]^{\text{T}}\), \({\mathbf{v}} = [F_{{x - {\text{des}}}} \;M_{{z - {\text{des}}}} ]{}^{\text{T}}\),

$${\mathbf{B}} = \frac{1}{R}\left[ {\begin{array}{*{20}c} {\cos \delta_{f} } & {\cos \delta_{f} } & 1 & 1 \\ { - d\cos \delta_{f} + a\sin \delta_{f} } & {d\cos \delta_{f} + a\sin \delta_{f} } & { - d} & d \\ \end{array} } \right].$$

For torque allocation, the friction ellipse constraint needs to be fully considered to ensure the feasibility of control:

$$F_{xij}^{2} + F_{yij}^{2} \le \left( {\mu_{ij} F_{zij} } \right)^{2}$$
(9)

where \(\mu_{ij}\) denote the road adhesion coefficient at each wheel, and \(F_{zij}\) stands for the vertical force. The lateral force \(F_{yij}\) can be obtained from the simplified tire model proposed in [2]:

$$F_{yij} = - K_{\alpha ij} \sqrt {1 - \left( {\frac{{F_{xij} }}{{\mu_{ij} F_{zij} }}} \right)^{2} } \frac{{\mu_{ij} }}{k}\tan^{ - 1} \left( {\frac{{K_{\alpha ij} \pi }}{{2\mu_{ij} F_{zij} }}\alpha_{ij} } \right)$$
(10)

where \(\alpha_{ij}\) and \(K_{\alpha ij}\) are the slip angle and lateral stiffness of each tire, respectively. Since there is a certain delay in the change of vertical load, the lateral tire force in the next sampling period can be estimated approximately according to the vertical load in the current sampling period and the longitudinal tire force in the next sampling period. The adhesion coefficient \(\mu_{ij}\) can be estimated in real time by the second-order nonlinear state observer proposed in [17]. The longitudinal tire force \(F_{xij}\) is related to the torque \(T_{ij}\) of the in-wheel motor:

$$\dot{\omega }_{ij} = \frac{1}{{J_{c} }}\left( {T_{ij} - F_{xij} R - M_{fij} } \right)$$
(11)

where \(M_{fij}\), \(\dot{\omega }_{ij}\), R and \(J_{c}\) are the rolling resistance moment, angular acceleration, rolling radius, and moment of inertia of the wheel, respectively.

The lower control level develops a weight-based optimal allocation algorithm, which selects the tire workload usages as the main optimization objective to reflect the stability margin. As this objective goes smaller, the stability margin of vehicle will be increased [1, 2]. The tire workload usage \(\Omega _{ij}\) can be described as

$$\Omega _{ij} = \frac{{F_{xij}^{2} }}{{\mu_{ij}^{2} F_{zij}^{2} }}$$
(12)

In previous studies, the tire workload usage of each wheel was often simply added as an overall optimization goal, regardless of the differences in adhesion condition at each wheel. However, this may result in some low-attachment wheels being unstable, while the torque of other wheels cannot be utilized to the maximum. Thus, the weight factor \(\psi_{ij}\) for \(\Omega _{ij}\) is investigated to suit different adhesion coefficients as follows:

$$\psi_{ij} = \frac{{\Omega _{ij} }}{{\sum {\Omega _{ij} } }}$$
(13)

In conclusion, the proposed torque allocation algorithm can be formulated as:

$$\hbox{min} \;J_{1} = \left\| {{\varvec{\Gamma}}\,{\mathbf{u}}} \right\|_{2}$$
(14)

where \({\mathbf{u}} = [T_{fl} \;T_{fr} \;T_{rl} \;T_{rr} ]^{\text{T}}\), \({\varvec{\Gamma}} = {\text{diag}}\left( {\frac{{\psi_{ij} }}{{\mu_{ij}^{{}} F_{zij}^{{}} R^{{}} }}} \right)\), R denotes the rolling radius. The constraints of optimal allocation can be described as:

$$\left\{ {\begin{array}{*{20}c} {F_{xij}^{2} + F_{yij}^{2} \le \left( {\mu_{ij} F_{zij} } \right)^{2} } \\ {{\mathbf{Bu}} = {\mathbf{v}}} \\ {{\mathbf{u}}_{{ \lim {-}}} \le {\mathbf{u}} \le {\mathbf{u}}_{{ \lim {+}}} } \\ \end{array} } \right.$$
(15)

where \({\mathbf{u}}_{{ \lim {-}}}\) and \({\mathbf{u}}_{{ \lim {+}}}\) are the lower limit and upper limit of u, respectively. Considering that the constraint strength of the equation is too strong to solve, it can be converted into a penalty term and introduced into (11), then:

$$\hbox{min} \;J_{2} = \left\| {{\varvec{\Gamma}}\,{\mathbf{u}}} \right\|_{2} + \xi \left\| {{\mathbf{W}}_{v} \left( {{\mathbf{Bu}} - {\mathbf{v}}} \right)} \right\|_{2}$$
(16)

where \(\xi\) and \({\mathbf{W}}_{v}\) denote the allocation weight coefficient and matrix, respectively. In particular, the \({\mathbf{W}}_{v}\) reflects the control priority of the yaw moment and traction force. For example, the control priority of the yaw moment is much higher than that of the traction force when the adhesion coefficient is low, so as to ensure good lateral stability.

The (16) can be reformulated as a general form:

$$J_{2} = \arg \mathop { \hbox{min} }\limits_{{\underline{{\mathbf{u}}} \le {\mathbf{u}} \le {\bar{\mathbf{u}}}}} \left\| {\left( {\begin{array}{*{20}c} {\xi^{{\frac{1}{2}}} {\mathbf{W}}_{v} {\mathbf{B}}} \\ {{\varvec{\Gamma}}_{1} } \\ \end{array} } \right){\mathbf{u}} - \left( {\begin{array}{*{20}c} {\xi^{{\frac{1}{2}}} {\mathbf{W}}_{v} {\mathbf{v}}} \\ 0 \\ \end{array} } \right)} \right\|_{2}^{2} = \left\| {{\mathbf{Au}} - {\mathbf{C}}} \right\|_{2}^{2}$$
(17)

The proposed optimization problem can be solved by the active set method [2].

3 Simulation Results

The adaptive steering stability control strategy proposed for the 4MIDEV was validated in the co-simulation with a strategy model in the Matlab/Simulink and a vehicle model in the Carsim, where the double-lane-change (DLC) maneuver was respectively carried out on the joint road and the μ-split road to further verify the adaptability of the strategy to the adhesion coefficient. In addition, the other two strategies, referred to as “ordinary control” and “speed control,” were compared with the proposed control strategy, referred to as “adaptive control.” The “ordinary control” proposed in [1] also developed a hierarchical control structure, but did not consider the influence of the adhesion coefficient. The “speed control” includes only the PID speed controller and a driver model to control lateral stability. The route of the DLC maneuver is shown in Fig. 3. The main parameters of the vehicle and hub motors for simulation are shown in Table 3.

Fig. 3
figure 3

Route of the DLC maneuver

Full size image
Table 3 The parameters of the vehicle and in-wheel motors
Full size table

3.1 μ-Split Road

In the simulation test for the μ-split road, the DLC maneuver was conducted at a constant speed of 60 km/h, where the adhesion coefficient was initially set to 0.75 and then changed to 0.75 on the right side and 0.2 on the left side at a distance of 105 m from the start, as shown in Fig. 4. Figure 5a–c show the track, yaw rate, and sideslip angle responses of the vehicle under aforementioned strategies, respectively. Although the adhesion coefficient changed, the adaptive control could better follow the desired trajectory, with the minimum error and the fastest stable speed. In addition, a good control effect of the yaw rate and sideslip angle was also guaranteed by the adaptive control. Compared with the general control, the error of these two quantities could be reduced by up to 55 and 58.8% respectively under the adaptive control. Figure 6f shows the phase plane of the sideslip angle and the sideslip angle rate. The curves of the speed control, general control, and adaptive control were gradually more concentrated on the origin, which means that the stability control effects of the above strategies were getting better [1].

Fig. 4
figure 4

μ-Split road

Full size image
Fig. 5
figure 5

Simulation results of the DLC maneuver under the μ-split road

Full size image
Fig. 6
figure 6

Joint road

Full size image

3.2 Joint Road

The DLC maneuver was then conducted on the joint road for further verification, where the vehicle kept a constant speed of 60 km/h. The setting of joint-road surface is shown in Fig. 6, the adhesion coefficient of which was initially set to 0.75 and then changed to 0.2 at the middle of the maneuver. Figure 7a–c show the track, yaw rate, and sideslip angle responses of the vehicle under above three strategies, respectively. The adaptive control showed the best control effect in the following of the target trajectory and could effectively reduce the control error of the yaw rate and sideslip angle after the change of adhesion coefficient. Figure 7f shows the phase plane of the sideslip angle and the sideslip angle rate. The curve of the adaptive control is most concentrated on the origin compared to those of the other two strategies, indicating that its stability control effect is the best.

Fig. 7
figure 7

Simulation results of the DLC maneuver under the joint road

Full size image

4 Conclusion

In this paper, an adaptive stability control strategy is proposed for the 4MIDEV to accommodate different adhesion coefficients. A new yaw moment control adapted to the adhesion coefficient is investigated in the upper control level to realize the comprehensive control of yaw rate and sideslip angle. The lower control level develops the optimization algorithm based on different weight coefficients, so as to realize different control of each motor torque according to the adhesion conditions at each wheel. The final simulation results show that the proposed control strategy can effectively improve the steering stability of the 4MDIEV on the road with different adhesion coefficients, such as on the joint road. In the future work, this strategy will verified by the hardware-in-the-loop simulation, and finally the real-car experiment will be also carried out.