1 Introduction

Fractional calculus represents a generalization of the classical differentiation and integration of nonnegative integer order to arbitrary order. This type of calculus has recently gained its importance and popularity because of the significant and interesting results which were obtained when fractional operators were utilized to model real-world problems in diversity of fields, e.g., physics, engineering, biology, etc. [1, 6, 12,13,14, 16, 23,24,25,26,27,28,29,30,31, 35, 37,38,39, 42, 43, 46, 47].

The Lagrangian and Hamiltonian mechanics are an alternate of the standard Newtonian mechanics. They are important because they can be used for the sake of solving any problem in the traditional mechanics. It is worth mentioning that in the Newtonian mechanics, the conception of force is needed. While, in the Lagrangian and Hamiltonian systems, the terms of energy are required.

Riewe [44, 45] was the first to consider the Lagrangian and Hamiltonian for a given dissipative system in the frame of fractional operators. Agarwal and Baleanu made significant contributions to the concept of fractional variational principles in [2,3,4,5, 19, 21].

In [2, 4, 20, 21, 40, 41], variety of optimization problems embodying constant order fractional control problems were considered. In [2, 4], the author proposed a general formulation for fractional optimal control problems and presented a solution scheme for such problems. This formulation was based on variation principles and Lagrange multipliers technique. In [40, 41], the authors extended the classical control theory to diffusion equations involving fractional operators in a bounded domain with and without a state constraints. These works were advanced in to a larger family of fractional optimal control systems containing constant orders in [11, 17]. Other contributions to this field were discussed in [18, 32, 33] and the references therein. Nevertheless, to the last extent of our knowledge, the area of calculus of variations and optimal control of fractional differential equations with variable order has been paid less attention than the case where fractional derivatives with constant orders. (see [15, 22, 36, 37]). This work is an attempt to fill this gap.

Motivated by what was mentioned above, we discuss the Lagrangian and Hamiltonian formalism for constrained systems in the presence of fractional variable order in this work.

Recently, in order to overcome the disadvantage of the existence of the singular kernels involved in the traditional fractional operators, Atangana and Baleanu [8] proposed a derivative with fractional order. The kernel involved in this derivative is nonlocal and nonsingular. Many researches have considered several applications on this fractional derivative (see e.g [7, 9, 48] and the references therein).

In this study, we use the aforementioned fractional derivative with variable order and propose to generalize the concept of equivalent Lagrangian for the fractional case. For a certain class of classical Lagrangian, there are several techniques to find the Euler–Lagrange equations and the associated Hamiltonians. However, the fractional dynamics depending on the fractional derivatives are used to construct the Lagrangian to begin with. Therefore, the existence of several options can be utilized to deal with a certain physical system. From this point of you, applications of the fractional derivative proposed by Atangana and Baleanu to the fractional dynamics may adduce new advantages in studying the constrained systems primarily because of the fact that there exist left and right derivatives of this kind. Addition, the fractional derivative of a function is given by a definite integral and it depends on the values of the function over the entire interval. Therefore, the fractional derivatives proposed are suitable to model systems with long-range interactions in space and/or time (memory) and process with many scales of space and/or time involved.

This work is organized as follows: In Sect. 2, we go over some concepts and definitions, and then we present the integration by parts formula in the framework of variable-order Atangana–Baleanu fractional time derivative. Section 3 includes a tabloid review of the fractional Lagrangian and Hamiltonian approaches in the frame of the proposed variable-order fractional derivatives and some detailed examples. In Sect. 4, we discuss constrained systems in the frame of the proposed derivative and investigate some example in details. In Sect. 5, the Fractional Optimal Control Problem (FOCP) is presented. Section 6 is dedicated to our conclusions.

2 Preliminaries

In this section, we present some definitions and notions related to Atangana–Baleanu fractional derivatives.

Let \(L^2(\varOmega )\) be the usual Hilbert space fitted to the scalar product (., .) and let \(H^m(\varOmega )\), \(H^m_ 0 (\varOmega )\) denote the usual Sobolev spaces.

First, lets recall the Mittag-Leffler function \(E_{\alpha (x),\beta }(u)\) for variable \(\alpha (x) \in (0,1)\) that is used in a great scale in this work and given below

$$ E_{\alpha (x),\beta }(u)=\sum _{k=0}^{\infty }\frac{u^k}{\varGamma (k\alpha (x)+\beta )},\, 0<\alpha (x)< 1, 0<\beta < 1, $$
$$ E_{\alpha (x),1}(u)=E_{\alpha (t)}(u),~ u\in \mathbb {C}, $$

where \(\varGamma (.)\) denotes the Gamma function defined as

$$ \varGamma (\alpha (x))=\int ^{\infty }_{0}s^{\alpha (x)-1}e^{-s}ds, ~ \mathfrak {R}{(\alpha (x)}>0. $$

It can be easily noticed that the exponential function is a particular case of the Mittag-Leffler function. In fact,

$$ E_{1,1}(u) = e^{u}, ~ E_{2,1}(u)=\cosh \sqrt{u},~ E_{1,2}(u)=\frac{e^{u}-1}{u}, ~~ E_{2,2}(u)=\frac{\sinh \sqrt{u}}{\sqrt{u}}. $$

A more generalized form of the Mittag-Leffler function is the Mittag-Leffler function with three parameters defined as

$$ E_{\alpha ,\beta }^{\lambda }(u)=\sum _{k=0}^{\infty }\frac{(\lambda )_{k}}{\varGamma (k\alpha +\beta )}\frac{u^k}{k!}, u,\beta , \lambda \in \mathbb {C},~ \mathfrak {R}{(\alpha )}>0, $$

where, \((\lambda )_{k}\) denotes the familiar Pochhammer symbol.

First of all, we present a new approach in defining variable-order Riemann–Liouville fractional integrals different from those in [10].

Definition 1

Let \(\phi (x)\) be an integrable defined on an interval [a, b] and a let \(\alpha (x)\) be function such that \(0<\alpha (x)\le 1\). We define the left Riemann–Liouville fractional integral of order \(\alpha (x]\) as

$$\begin{aligned} ~_{a}I^{\alpha (.)}\phi (x)=\frac{1}{\varGamma (\alpha (x))}\int _a^x (x-s)^{\alpha (x)-1}\phi (s)ds \end{aligned}$$
(1)

and

$$\begin{aligned} ~_{a}\mathscr {I}^{\alpha (.)}\phi (x)=\int _a^x (x-s)^{\alpha (s)-1}\phi (s)\frac{1}{\varGamma (\alpha (s))}ds. \end{aligned}$$
(2)

In the right case, we have

$$\begin{aligned} I_b^{\alpha (.)}\phi (x)=\frac{1}{\varGamma (\alpha (x))}\int _x^b (s-x)^{\alpha (x)-1}\phi (s)ds \end{aligned}$$
(3)

and

$$\begin{aligned} \mathscr {I}_b^{\alpha (.)}\phi (x)=\int _t^b (s-x)^{\alpha (s)-1}\phi (s)\frac{1}{\varGamma (\alpha (s))}ds. \end{aligned}$$
(4)

To define fractional integral type operators with variable order, we follow [34].

Definition 2

$$\begin{aligned} \mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}\varphi (x)=\frac{B(\alpha (x))}{1-\alpha (x)}\int _a^x E_{\alpha (x)} \left[ \frac{-\alpha (x)}{1-\alpha (x)} (x-s)^{\alpha (x)}\right] \varphi (s) ds,~~x>a. \end{aligned}$$
(5)

Similarly, we define the right generalized fractional integral as

$$\begin{aligned} \mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}\varphi (x)=\frac{B(\alpha (x))}{1-\alpha (x)}\int _t^b E_{\alpha (x)} \left[ \frac{-\alpha (x)}{1-\alpha (x)}(s-x)^{\alpha (x)}\right] \varphi (s) ds,~~x<b. \end{aligned}$$
(6)

We define the following operators as well:

$$\begin{aligned} \mathscr {E}_{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}\varphi (x)=\int _a^x \frac{B(\alpha (s))}{1-\alpha (s)} E_{\alpha (s)} \left[ \frac{-\alpha (s)}{1-\alpha (s)} (x-s)^{\alpha (s)}\right] \varphi (s) ds,~~x>a \end{aligned}$$
(7)

and

$$\begin{aligned} \mathscr {E}_{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}\varphi (x)=\int _x^b \frac{B(\alpha (s))}{1-\alpha (s)} E_{\alpha (s)} \left[ \frac{-\alpha (s)}{1-\alpha (s)}(s-x)^{\alpha (s)}\right] \varphi (s) ds,~~x<b. \end{aligned}$$
(8)

Now, we present the definitions of the fractional integrals and derivatives of variable order in the point of view of Atangana–Baleanu [7].

Definition 3

For a given function \(u\in H^{1}(a, b), b > a\), \(\alpha (x) \in (0,1)\), the Atangana–Baleanu fractional integrals (AB integral) of variable order \(\alpha (x)\) of a given function \(u\in H^{1}(a, b), b>x> a\) (where A denotes Atangana, B denotes Baleanu) with base point a is defined at a point \(x\in (a, b)\) by

$$\begin{aligned} \begin{array}{ccc} ^{AB}_{ \,\,\,a}I_{x}^{\alpha (x)}u(x)&{}=&{} \frac{1-\alpha (x)}{B(\alpha (x))}u(t)+\frac{\alpha (x)}{B(\alpha (x))\varGamma (\alpha (x))}\int _{a}^{x}u(s)(x-s)^{\alpha (x)-1}ds, ~~\text{(left } \text{ ABI) }\\ &{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\frac{\alpha (x)}{B(\alpha (x))}\,_{a}I_{x}^{\alpha (x)}u(x)\end{array} \end{aligned}$$
(9)

and

$$\begin{aligned} \begin{array}{ccc} ^{AB}_{ \,\,\,x}I_{b}^{\alpha (x)}u(x)&{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\frac{\alpha (x)}{B(\alpha (x))\varGamma (\alpha (x))}\int _{x}^{b}u(s)(s-x)^{\alpha (x)-1}ds, ~~\text{(right } \text{ ABI) }\\ &{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\frac{\alpha (x)}{B(\alpha (x))}\,_{x}I_{b}^{\alpha (x)}u(x).\end{array} \end{aligned}$$
(10)
$$\begin{aligned} \begin{array}{ccc} ^{AB}_{ \,\,\,a}{\mathscr {I}}_{x}^{\alpha (x)}u(x)&{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\int _{a}^{x}\frac{\alpha (s)}{B(\alpha (s))\varGamma (\alpha (s))}u(s)(x-s)^{\alpha (s)-1}ds, ~~\text{(left } \text{ AB }{\mathscr {I}})\\ &{}=&{}\frac{1-\alpha (x)}{B(\alpha (t))}u(x)+\,_{a}{\mathscr {I}}_{x}^{\alpha (x)}\left[ \frac{\alpha (x)}{B(\alpha (x))}u(x)\right] \end{array} \end{aligned}$$
(11)

and

$$\begin{aligned} \begin{array}{ccc} ~^{AB}_{ ~\,\,x}{\mathscr {I}}_{b}^{\alpha (x)}u(x)&{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\int _{x}^{b}\frac{\alpha (s)}{B(\alpha (s))\varGamma (\alpha (s))}u(s)(s-x)^{\alpha (s)-1}ds, ~~\text{(right } \text{ AB }{{\mathscr {I}})}\\ &{}=&{}\frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\,{\mathscr {I}}_b^{\alpha (x)}\left[ \frac{\alpha (x)}{B(\alpha (x))}u(x)\right] .\end{array} \end{aligned}$$
(12)

Once one takes \(\alpha (x) =0\) in (9), (10) we recover the initial function and when \(\alpha (x) =1\) is considered in (9), (10) we recover the ordinary integral.

The Atangana–Baleanu fractional derivatives in the Riemann–Liouville sense (ABR derivative) of variable order \(\alpha (x)\) for a given function \(\varphi (x)\in H^{1}(a, b), b>x> a\) (where R denotes Riemann) with base point a is defined at a point \(x\in (a, b)\) by

$$\begin{aligned} ^{ABR}_{~ \,\,\,a}D_{x}^{\alpha (x)}\varphi (x)=\frac{d}{dx}{} \mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}\varphi (x) ~~\text{(left } \text{ ABRD) } \end{aligned}$$
(13)
$$\begin{aligned} ^{ABR}_{~ \,\,\,x}D_{b}^{\alpha (t)}\varphi (x)=-\frac{d}{dt} \mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}\varphi (x) ~~\text{(right } \text{ ABRD) }, \end{aligned}$$
(14)
$$\begin{aligned} ^{ABR}_{~\,\,\,a}{\mathscr {D}}_{x}^{\alpha (t)}\varphi (x)=\frac{d}{dx} \mathscr {E}_{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}\varphi (x) ~~\text{(left } \text{ ABR }{\mathscr {D}}) \end{aligned}$$
(15)
$$\begin{aligned} ^{ABR}_{~ \,\,\,x}{\mathscr {D}}_{b}^{\alpha (x)}\varphi (t)=-\frac{d}{dx} \mathscr {E}_{\alpha (t), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}\varphi (x) ~~\text{(right } \text{ ABR }{\mathscr {D}}) \end{aligned}$$
(16)

and the Caputo Atangana–Baleanu fractional derivatives (ABC derivative) of variable order \(\alpha (x)\) for a given function \(\varphi (x)\in H^{1}(a, b), b>x> a\) (where C denotes Caputo) with base point a is defined at a point \(x\in (a, b)\) by

(17)
(18)
(19)
(20)

Remark 1

If one replace \(\alpha (x)\) in (5) and (6) by \(\alpha (x-s)\) and replaces each \(\alpha (s)\) in (7) and (8) by \(\alpha (x-s)\), then the ABR and ABC fractional derivatives with variable order can be expressed in the convolution form. Analogously, if one replaces \(\alpha (x)\) in (9) and (10) by \(\alpha (x-s)\) and replaces each \(\alpha (s)\) in (11) and (12) by \(\alpha (x-s)\), then the second part of the AB fractional integrals with variable order can be expressed in the convolution form.

Lemma 1

For functions u and v defined on [a, b] and \(0<\alpha (x)\le 1\) we have

$$\begin{aligned} \int _a^b u(x) ~_{a}I_x^{\alpha (x)} v(x)dx=\int _a^b v(x) ~_{x}\mathscr {I}_b^{\alpha (x)} u(x)dx, \end{aligned}$$
(21)
$$\begin{aligned} \int _a^b u(x) ~_{a}\mathscr {I}_x^{\alpha (x)} v(x)dt=\int _a^b v(x) ~_{x}I_b^{\alpha (x)} u(x)dx. \end{aligned}$$
(22)

Proof

Using Definition 1 and changing the order of integration, we have

$$\begin{aligned} \nonumber \int _a^b u(x) ~_{a}I_x^{\alpha (x)} v(x)dx= & {} \int _a^b u(x)\left( \frac{1}{\varGamma (\alpha (x))} \int _a^x (x-s)^{\alpha (x)-1}v(s)ds\right) dx\\ \nonumber= & {} \int _a^b v(s) \left( \int _s^b (x-s)^{\alpha (x)-1} \frac{u(x)}{\varGamma (\alpha (x))}dx \right) ds \\= & {} \int _a^b v(s) ~_{s}\mathscr {I}_b^{\alpha (s)} u(s)ds. \end{aligned}$$

On the other side, again using Definition 1 and changing the order of integrations, we get

$$\begin{aligned} \nonumber \int _a^b u(x) ~_{a}\mathscr {I}_x^{\alpha (x)} v(x)dx= & {} \int _a^b u(x)\left( \int _a^x (x-s)^{\alpha (s)-1} v(s) \frac{ds}{\varGamma (\alpha (s))}\right) dx\\ \nonumber= & {} \int _a^b v(s) \left( \frac{1}{\varGamma (\alpha (s))}\int _s^b u(x) (x-s)^{\alpha (s)-1} dx \right) ds\\= & {} \int _a^b v(s) ~_{x}I_b^{\alpha (s)} u(s)ds \end{aligned}$$

Now, benefiting from Lemma 1 we can show that the following integration by parts formulas hold.

Theorem 1

(Integration by parts for AB fractional integrals) Let \(\alpha (x)>0,\, p\ge 1,\, q\ge 1\), and \(\frac{1}{p}+\frac{1}{q}\le 1+\alpha (x)\) for all t. Then for any \(u(x)\in L^{p}(a,b),v(x)\in L^q(a,b)\), we have

$$\begin{aligned} \int _a^b u(t) ~^{AB}_{~ a}I_x^{\alpha (x)} v(x)dt=\int _a^b v(x) ~^{AB}_{~ x}\mathscr {I}_b^{\alpha (x)} u(x)dx, \end{aligned}$$
(23)
$$\begin{aligned} \int _a^b u(x) ~^{AB}_{~ a}\mathscr {I}_x^{\alpha (x)} v(x)dx=\int _a^b v(x) ~^{AB}_{~ x}I_b^{\alpha (x)} u(x)dx. \end{aligned}$$
(24)

Proof

From Definition 3 and by applying the first part of Lemma 1, we have

$$\begin{aligned} \nonumber \int _a^b u(x) ~^{AB}_{a}I_x^{\alpha (x)} v(x)dt= & {} \int _a^b v(x) \frac{1-\alpha (x)}{B(\alpha (x))}u(x) dx+\int _a^b u(x)\frac{\alpha (x)}{B(\alpha (x))}~_{a}I_x^{\alpha (x)}v(x)dx \\ \nonumber= & {} \int _a^b v(x) \frac{1-\alpha (x)}{B(\alpha (x)}u(x) dx+\int _a^b v(t) _{ ~x}\mathscr {I}_b^{\alpha (x)} \left[ \frac{u(x) \alpha (x)}{B(\alpha (x))}\right] dx \\= & {} \int _a^b v(x)\left( \frac{1-\alpha (x)}{B(\alpha (x))}u(x)+\,_{~x}{\mathscr {I}}_b^{\alpha (x)}[\frac{\alpha (x)}{B(\alpha (x))}u(x)]\right) dx \\= & {} \int _a^b v(x) ~^{AB}_{x}\mathscr {I}_b^{\alpha (x)} u(x)dx. \end{aligned}$$

The proof of the formula in (24) can be done similarly, once we use the second part of Lemma 1.

Lemma 2

Let u(x) and v(x) be functions defined on [a, b] and let \(0<\alpha (x)\le 1\). Then, we have

$$\begin{aligned} \int _a^b u(x)\mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}v(x) dx=\int _a^b v(x) \mathscr {E}_{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}u(x) dx, \end{aligned}$$
(25)
$$\begin{aligned} \int _a^b u(x) \mathscr {E}_{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}v(x) dx=\int _a^b v(x) \mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},b^-}u(x) dx. \end{aligned}$$
(26)

Proof

The proof can be executed using some definitions and changing the order of integrations. In fact, we have

\(\displaystyle \int _a^b u(x)\mathbf E _{\alpha (x), 1, \frac{-\alpha (x)}{1-\alpha (x)},a^+}v(x) dx\)

\(\displaystyle =\int _a^b u(x) \frac{B(\alpha (x))}{1-\alpha (x)} \left( \int _a^x v(s) E_{\alpha (x)}(\frac{-\alpha (x)}{1-\alpha (x)} (x-s)^{\alpha (x)})ds\right) dx\)

\(\displaystyle = \int _a^b v(s) \left( \int _s^b \frac{B(\alpha (x))}{1-\alpha (x)} E_{\alpha (x)}(\frac{-\alpha (x)}{1-\alpha (x)} (x-s)^{\alpha (x)})u(x)dx\right) ds\)

\(\displaystyle =\int _a^b v(s) \mathscr {E}_{\alpha (s), 1, \frac{-\alpha (s)}{1-\alpha (s)},b^-}u(s) ds\).

The formula in (26) can proved similarly.

Theorem 2

Let u(x) and v(x) be functions defined on [a, b] and let \(0<\alpha (x)\le 1\). We have

(27)
(28)
(29)

and

(30)

Proof

The proof follows from Definition 3, Lemma 2 and the classical integration by parts. Bellow, we prove (27) only. The proofs of the rest of the formulas are analogous. Actually, using Definition 3 and applying the first part of Lemma 2 and the traditional integration by parts, we have

(31)

3 Fractional Variational Principles in the Frame of Variable-Order Fractional Atangana–Baleanu’s Derivatives

In this section, we present Euler–Lagrange and fractional Hamilton equations in the frame of the fractional variable-order Atangana–Baleanu derivatives are.

Theorem 3

Let J[z] be a functional of the form

(32)

defined by the set of functions which have continuous variable-order Atangana–Baleanu fractional derivative in the Caputo sense on the set of order \(\alpha (x)\) in [a, b] and which satisfy the boundary conditions \(z(a)=z_{a}\) and \(z(b)=z_{b}\). Then a necessary condition for J[z] to have a maximum for given function z(x) is that z(x) must satisfy the following Euler–Lagrange equation:

(33)

Proof

To obtain the necessary conditions for the extremum, we assume that \(z^{*}(x)\) is the desired function. Let \(\varepsilon \in R\) define a family of curves

$$\begin{aligned} z(x)=z^{*}(x)+\varepsilon \eta (x) \end{aligned}$$
(34)

where, \(\eta (t)\) is an arbitrary curve except that it satisfies the homogeneous boundary conditions; that is

$$\begin{aligned} \eta (a) = \eta (b) = 0. \end{aligned}$$
(35)

To obtain the Euler–Lagrange equation, we substitute equation (34) into Eq. (32) and differentiate the resulting equation with respect to \(\varepsilon \) and set the result to 0. This leads to the following condition for extremum:

(36)

Using Eqs. (30), (36) can be written as

(37)

We call , the natural boundary condition. Now, since \(\eta (x)\) is arbitrary, it follows from a well established result in calculus of variations that

(38)

Equation (38) is the Generalized Euler–Lagrange Equation GELE for the Fractional Calculus Variation (FCV) problem defined in terms of the variable-order Atangana–Baleanu Fractional Derivatives ABFD. Note that the Atangana–Baleanu derivatives in the Caputo and Riemann–Liouville sense appears in the resulting differential equations.

Example 1

Consider the following Lagrangian:

(39)

then independent fractional Euler–Lagrange equation (38) is given by

(40)

Example 2

We consider now a fractional Lagrangian of the oscillatory system

(41)

where m the mass and k is constant. Then the fractional Euler–Lagrange equation is

(42)

This equation reduces to the equation of motion of the harmonic oscillator when \(\alpha (x) \rightarrow 1\).

3.1 Some Generalizations

In this section, we extend the results obtained in give some Theorem 3.1 to the case of n variables \(z_1(x), z_2(x),..., z_n(x)\). We denote by \(\mathscr {F}_n\) the set of all functions which have continuous left ABC fractional derivative of order \(\alpha (x)\) and right ABC fractional derivative of order \(\beta \) for \(x\in [a, b]\) and satisfy the conditions

$$ z_i(a) = z_{ia} , z_i(b) = z_{ib}, i = 1,2,...,n. $$

The problem can be defined as follows: find the functions \(z_1,z_2,...,z_n\) from \(\mathscr {F}_n\), for which the functional

has an extremum, where \(L(x,z_1,...,z_n,y_1,...,y_n,w_1,...,w_n)\) is a function with continuous first and second partial derivatives with respect to all its arguments. A necessary condition for \(J[z_1,z_2,...,z_n]\) to admit an extremum is that \(z_1(x), z_2(x),..., z_n(x)\) satisfy Euler–Lagrange equations:

(43)

Example 3

Lets consider the system of two planar pendula, both of length l and mass m, suspended from the same distance apart on a horizontal line so that they are moving in the same plane. The fractional counter part of the Lagrangian is

(44)

To obtain the fractional Euler–Lagrange equation, we use

(45)

It follows that

(46)

These equation reduces to the equation of motion of the harmonic oscillator when \(\alpha (t) \rightarrow 1\).

$$\begin{aligned} z_1^{\prime \prime }+\frac{g}{l}z_1=0,\quad z_2^{\prime \prime }+\frac{g}{l}z_2=0 \end{aligned}$$
(47)

4 Fractional Variational Principles and Constrained Systems in the Frame of Variable-Order Atangana–Baleanu’s Derivatives

Lets now consider the following problem: Find the extremum of the functional

subject to the dynamical constraint

with the boundary conditions

$$ x(a)=x_a, \quad x(b)=x_{b}. $$

In this case, we define the functional

$$ S[x]=\int _{a}^{b}[L+\lambda \varPhi ]dx, $$

where

and \(\lambda \) is the Lagrange multiplier. Then Eq. (38) in this case takes the form

(48)

which can be written as

(49)

Example 4

Lets consider

with the boundary conditions

$$ z(0)=0, \quad z(1)=0, $$
$$ \int _{0}^{1}zdx=0,\quad \int _{0}^{1}xzdx=1. $$

Then we have

where \(\lambda _1, \lambda _2\) are the Lagrange multipliers. Then Eq. (48) takes the form

(50)

5 Fractional Optimal Control Problem Involving Variable-Order Atangana–Baleanu’s Derivatives

Find the optimal control v(t) for a that minimizes the performance index

$$\begin{aligned} J[v]=\int _{0}^{1}F(z,v,x)dx, \end{aligned}$$
(51)

subject to the dynamical constraint

(52)

with the boundary conditions

$$\begin{aligned} z(0)=z_0. \end{aligned}$$
(53)

where z(x) is the state variable, x represents the time, and F and G are two arbitrary functions. Note that Eq. (51) may also include some additional terms containing state variables at the end point. This term in not considered here for simplicity. When \(\alpha (x) = 1\), the above problem reduces to the standard optimal control problem. To find the optimal control we follow the traditional approach and define a modified performance index.

Lets define the functional

(54)

where \(\lambda \) is the Lagrange multiplier. The variations of Equation (54) give

(55)

Using Eqs. (27), (55) becomes

(56)

where \(\delta z(0) = 0\) or \(\lambda (0) = 0\), and \(\lambda z(1) = 0\) or \(\lambda (1) = 0\). Because z(0) is specified, we have \(\delta z(0) = 0\), and since z(1) is not specified, we require \(\lambda (1)=0\). Using these assumptions, Eqs. (55) and (56) become

(57)

Since \({\mathscr {J}}[v]\) and consequently J(v)) is minimized, \(\delta z, \delta v\), and \( \delta \lambda \) in Eq. (57) are all equal to zero. This gives

(58)
$$\begin{aligned} \,^{ABR}_{\quad \,\,\,x}{\mathscr {D}}_{1}^{\alpha (x)}\lambda =\frac{\partial F}{\partial z}+\lambda \frac{\partial G}{\partial z} \end{aligned}$$
(59)
$$\begin{aligned} \frac{\partial F}{\partial v}+\lambda \frac{\partial G}{\partial v}=0. \end{aligned}$$
(60)

and

$$\begin{aligned} z(0) = z_{0}\,~ \text{ and }~\, \lambda (1) = 0. \end{aligned}$$
(61)

Observe that Eq. (58) contains Left Atangana–Baleanu in Caputo sense FD, whereas Eq. (59) contains Right Atangana–Baleanu in Caputo FD. This clearly indicates that the solution of optimal control problems requires knowledge of not only forward derivatives but also backward derivatives to count on the end conditions. In classical optimal control theories, this issue is either not discussed or they are not clearly stated. This is largely because the backward derivative of order 1 turns out to be the negative of the forward derivative of order 1.

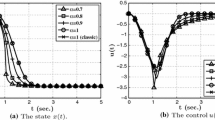
Example 5

Consider

$$\begin{aligned} J[v]=\frac{1}{2}\int _{0}^{1}[a(x)z^{2}(x)+b(x)v^{2}(x)]dx, \end{aligned}$$
(62)

where \(a(x)\ge 0\), \(b(x)> 0\), and,

(63)

This linear system for \(\alpha (t)= 1\) and \(0< \alpha (t)< 1\) was considered before in the literature and formulations and solution schemes for this system within the traditional Riemann–Liouville and Caputo derivatives are addressed in many books and articles (see e.g. [2, 3]. Here, we discuss the same problem in the framework of Atangana–Baleanu fractional derivatives. For \(0< \alpha (t)< 1\), the Euler–Lagrange Equations (58) to (60) gives (63) and

$$\begin{aligned} ^{ABR}_{\quad \,\,\,x}{\mathscr {D}}_{1}^{\alpha (x)}\lambda = a(x)z(x) + c(x)\lambda , \end{aligned}$$
(64)

and

$$\begin{aligned} b (x)v(x) + d(x)\lambda = 0. \end{aligned}$$
(65)

From (63) and (65), we obtain

(66)

Thus, z(x) and \(\lambda (x)\) can be computed from (64) and (66).

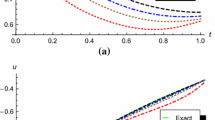
Example 6

Consider the following time-invariant problem.

Find the control v(x) which minimizes the quadratic performance index

$$\begin{aligned} J[v]=\frac{1}{2}\int _{0}^{1}[z^{2}(z)+v^{2}(x)]dx, \end{aligned}$$
(67)

subject to

(68)

and the initial condition

$$\begin{aligned} z(0) = 1. \end{aligned}$$
(69)

Note that from (5), we have

$$\begin{aligned} a(x) = b (x) = -c(x) = d(x) = z_{0} = 1, \end{aligned}$$
(70)

and (64) and (65) read

$$\begin{aligned} ^{ABR}_{\quad \,\,\,t}{\mathscr {D}}_{1}^{\alpha (x)} \lambda = z-\lambda \end{aligned}$$
(71)

and

$$\begin{aligned} v + \lambda = 0. \end{aligned}$$
(72)

6 Conclusions

In this work, we have tackled some types of optimal control problems in the presence of the newly proposed nonlocal and nonsingular fractional derivatives that involve Mittag-Leffler functions as kernels. In order to obtain Euler–Lagrange equations, we exploited the techniques mentioned in several books and the fractional integration by parts formulas. It turned out, the formulation shewed and the obtained equations are analogous with the ones when the classical variation principles are used; but with slight differences. That is, all the concepts of the classical calculus of variation can be carried to fractional calculus of variation in the frame of either the traditional fractional operators with singular kernels or the newly defined operators involving nonsingular kernel. However, since there is a little advance that has been done in the theory of fractional operators with variable order, there is no big progress in the calculus of variation in the presence of such operators. Therefore, we believe in the need of tackling such operators and that this work may initiate the interest of researches and them as they can also be used in modeling some problems considered in various fields of sciences.