Studies on Transport of Reactive and Non-reactive Elements in Fractured Media

Abstract

In recent years, the focus has been shifted to groundwater quality because the consumptive lifestyle has been the reason for deterioration of groundwater. The contaminant transport in the subsurface has to be studied to know the extent of contaminant transport and also know the final magnitude of contaminant. Normally, these contaminants travel through a saturated or unsaturated porous media and sometimes fractured till clays or silts are encountered in the surroundings. The contaminant transport is very different when it has to travel through a fractured media as the hydraulic conductivity is high in the fractures even though the porosity is low, and hence makes it a very important topic of discussion. In the present study, a numerical model for contaminant transport in fractured porous media has been presented. Transport process in single fracture–matrix system is described by two coupled equations, one for fracture and other for matrix. Analysis is performed using meshfree method called element-free Galerkin method. A FORTRAN programme has been developed to obtain numerical solution, and it is validated with the results in the literature. Overall, the results predicted are found in good agreement. Parametric study has been performed to examine the transport of different reactive and non-reactive elements in the fractured media by varying their dispersivity, retardation factor and dispersion coefficient. Parameters of fracture like fracture thickness and hydraulic conductivity shall be varied to observe the transport of these elements in fractured porous media.

1 Introduction

In recent years, the focus has drifted from water supply to groundwater quality. The present consumptive lifestyle has deteriorated the groundwater quality, and it is evident from the contamination of groundwater reserves as well as rivers and lakes. Often the time taken to identify the contamination of groundwater is large, and it is difficult to apply remedial measures, and hence the focus is to reduce the emission of contaminants in the system. The contaminants are transported by advection, dispersion and retardation, but the behaviour of contaminants in fracture media is slightly different. In fractured zones, porosity is low but still the groundwater velocities are higher. Fractures, offer least hydraulic resistance and the contaminant will enter the system primarily through the fractures. Matrix diffusion from the fractures to the porous matrix constitutes in removing contaminant from the primary flow channels, and hence it acts as a dynamic storage mechanism within the fracture flow system. As a result, contaminant transport in fractured porous media can be different from contaminant transport in porous granular media in the conventional sense, where such a mechanism is not generally represented (Freeze and Cherry 1979). Solute transport through fractured porous media has been studied by many researchers in the past decade. Grisak and Pickens (1980) developed a finite element model for transport in fracture and matrix. The model was developed by considering two-dimensional transport by dividing the subregions into linear triangular elements and assigning each element of different properties. Tang et al. (1981) developed an analytical solution considering coupling of matrix flux in fracture and matrix. Wu et al. (2010) proposed a conceptual model of fracture-flow-enhanced matrix diffusion, which correlates with fracture flow velocity. The proposed model incorporated an additional matrix diffusion process, which was induced by rapid fluid flow along the fractures.

Sharma and Dixit (2014) conducted experimental study to investigate the behaviour of solute transport in fractured media. Sharma and Srivastava (2012) developed an implicit finite difference model to observe the reactive transport in fracture and matrix simultaneously. The model is useful for remediation of fractured porous media and disposal of hazardous waste material. In recent years, meshfree methods are getting attention as they aim to eliminate the structure of mesh and construct approximate solutions for the equations in terms of nodes (Liu and Gu 2005). Most common and successful meshfree method is the element-free Galerkin method (EFGM) and has been used for solving boundary value problems related to various field studies (Belytschko et al. 1994; Kumar and Dodagoudar 2008, 2009; Mategaonkar and Eldho 2012; Satavalekar and Sawant 2015).

In this paper, contaminant transports for different ions like Cl⁻, Na⁺, F⁻, Mg²⁺, Ca²⁺ and Cu²⁺ (non-reactive and reactive ions) have been observed through a fracture–matrix-saturated porous media, modelled using Element-Free Galerkin Method (EFGM). The governing equation employed is one-dimensional two-coupled contaminant transport through the fracture–matrix porous media. A detailed parametric study is conducted to examine the effect of velocity in fracture and matrix diffusion on the transport of contaminant in the media.

2 Methodology

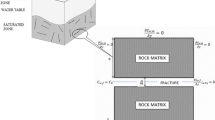
The conceptual model is presented in Fig. 1. Transport process in single fracture–matrix system is described by two coupled equations, one for fracture and other for matrix. The coupling is incorporated through continuity of fluxes and concentrations along the interface. Groundwater velocity in fracture is assumed constant. The solute source is considered at the inlet of the fracture. The width of fracture is much smaller than the length, and the migration of contaminant is faster in fracture than matrix. The diffusive flux from fracture to matrix takes place perpendicular to the fracture.

Fig. 1

Domain of fracture–matrix media

Linear diffusive transport equilibrium equation for the concentration of solute in the solution along the matrix C_m (M/L³) considering sorption, diffusion and first-order degradation for porous matrix (Tang et al. 1981) is written as

$$R_{m} \frac{{\partial C_{m} }}{\partial t} - D_{xm} \frac{{\partial^{2} C_{m} }}{{\partial x^{2} }} - D_{zm} \frac{{\partial^{2} C_{m} }}{{\partial z^{2} }} + \lambda C_{m} = 0$$

(1)

in which, D_xm and D_zm are the diffusive flux in the matrix in the x- and z-directions (L²/T), λ is the decay constant (T⁻¹) and R_m is the retardation factor in matrix. Retardation factor R_m is related to bulk density of soil matrix ρ_b (M/L³), distribution coefficient K_m (L³/M) and matrix porosity θ as $R_{m} = 1 + \left( {k_{m} \rho_{b} /\theta } \right)$

One-dimensional transport equation for the concentration of solute in the solution along the fracture C_f (M/L³) including linear equilibrium sorption and first-order degradation for fracture (Tang et al. 1981) is written as

$$R_{f} \frac{{\partial C_{f} }}{\partial t} - D_{f} \frac{{\partial^{2} C_{f} }}{{\partial z^{2} }} - \frac{{\theta D_{xm} }}{b}\frac{{\partial C_{m} }}{\partial x} + v_{f} \frac{{\partial C_{f} }}{\partial z} + \lambda C_{f} = 0$$

(2)

where b is the half-aperture (L), λ is the decay constant (T⁻¹) and D_f is the diffusive flux in the fracture (L²/T) given as $D_{f} = \alpha_{f} v_{f} + D_{m}$. R_f is the retardation factor in fracture related to distribution coefficient in fracture K_f (L³/M) as $R_{f} = 1 + {{k_{f} } \mathord{\left/ {\vphantom {{k_{f} } b}} \right. \kern-0pt} b}$. α_f is the dispersivity in the direction of fracture axis.

Third term in Eq. 2, $\frac{{\theta D_{xm} }}{b}\frac{{\partial C_{m} }}{\partial x}$ is the coupling term, which provides the continuity of fluxes and concentrations along the interface of the boundary.

The following initial and boundary condition for fracture and porous matrix are used:

Initial condition

$$C_{f} (x,0) = 0{\kern 1pt} \;;\quad \left. {\frac{{\partial C_{f} }}{\partial z}} \right|_{(\infty ,t)} = 0$$

(3)

Constant-type boundary condition

$$\begin{aligned} & C_{f} (0,t) = C_{0} \\ & C_{m} (x,z,0) = 0\;;\;C_{m} (x,b,t) = C_{f} (z,t){\kern 1pt} ;\;\left. {\frac{{\partial C_{m} }}{\partial x}} \right|_{(x,L,t)} = 0 \\ \end{aligned}$$

(4)

where C₀ is the initial concentration injected at the inlet of the fracture (M/L³), EFGM uses only set of nodes to model the boundary and generate discrete equations. It employs moving least squares (MLS) approximants formulated by Lancaster and Salkauskas (1981) to approximate the function C(x) with C^h(x) in which C(x) is the contaminant concentration at x, where x is a position coordinate. EFGM does not satisfy the Kronecker delta criterion, and hence the Lagrangian multiplier technique (Dolbow and Belytschko 1998) is used to enforce the Dirichlet boundary condition. A detailed mathematical formulation and algorithm referred from Satavalekar (2015) and Satavalekar and Sawant (2015).

3 Model Verification

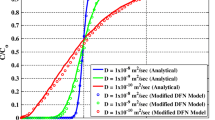
The model developed using element-free Galerkin method is verified with the results of Tang et al. (1981). Tang et al. (1981) analysed the one-dimensional two-coupled equation for fracture and matrix by developing a general analytical solution. Tang et al. (1981) considered one-dimensional flow in both fracture and matrix, and the coupling of fluxes was provided along the interface. The material properties are mentioned in Table 1 used in the present study. Sensitivity analysis is carried out with nodes varying from 11 × 11, 21 × 21 and 51 × 11. The results for the variation in normalized concentration with distance along fracture at last time step are presented in Fig. 2. It can be observed from Fig. 2 that the results by EFGM using 21 × 21 nodes are in good agreement with the results obtained by Tang et al. (1981). The domain of the fracture–matrix system is presented in Fig. 1. The fracture is a one-dimensional model, and the matrix is a two-dimensional model. The Dirichlet boundary is at the first node of the fracture.

Table 1 Material properties, Tang et al. (1981)

Fig. 2

Comparison of EFGM results with Tang et al. (1981)

4 Parametric Study

A parametric study is performed considering ions like Cl⁻, Na⁺, F⁻, Mg²⁺, Ca²⁺ and Cu²⁺. The diffusion and distribution coefficients of these ions are presented in Table 2. These values have been referred from Shackelford and Daniel (1991), Chakraborty and Ghosh (2010), Sharma and Dixit (2014) and Tombul et al. (2005). A parametric study considering variation in fracture velocity and dispersivity has been performed. Parametric study provides a better idea of migration of contaminant when a particular parameter is changed. Material properties considered in the parametric study are reported in Table 2 except for the values of diffusion coefficient and time. The diffusion coefficient for different ions is considered from Table 3, and time of 100 days is considered. In the study, a particular parameter under consideration (whose effect is to be examined) is varied, while the other parameters are kept constant as reported in Table 1.

Table 2 Material properties, Grisak and Pickens (1980)

Table 3 Material properties of different ions

4.1 Effect of Velocity

In this section, the effect of change of flow velocity in fracture is observed on the transport of different ions presented in Table 3 while maintaining other parameters like diffusion coefficient, dispersivity, distribution factor, aperture size same as reported in Tables 2 and 3. The fracture velocity is varied as 0.3 and 0.6 m/day, and the effect is presented in Fig. 3 for distance 0.76 m and time 100 days. From Fig. 3a, it can be observed that with a fracture velocity of 0.6 m/day, chloride ions (Cl⁻) migrate faster and at the end of the fracture (0.76 m) will have a final normalized concentration of 0.95, whereas F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺ have final normalized concentration of 0.92, 0.9, 0.75, 0.9 and 0.78 as these ions are reactive in nature and concentration reduces due to adsorption of these in the matrix. From Fig. 3b, it can be observed that with a flow velocity of 0.3 m/day, chloride ions (Cl⁻) migrate faster and at the end of the fracture (0.76 m) will have a final normalized concentration of 0.86, whereas F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺ have final normalized concentration of 0.83, 0.8, 0.53, 0.77 and 0.53. By reduction of velocity by half, the concentrations of Cl⁻, F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺ are reduced by 9, 11, 12, 28, 15 and 31%, respectively. It is observed that when the flow velocity of fracture is lower, the transport of contaminant is lesser and it varies for different ions. Non-reactive ions having zero distribution coefficient observe faster transport as compared to ions having tendency to retard due to adsorption. Similar results were also reported by Grisak and Pickens (1980, 1984).

Fig. 3

Effect of velocity on concentration

4.2 Effect of Fracture Aperture

In this section, the effect of fracture aperture is observed on the transport of different ions presented in Table 3 while maintaining other parameters like diffusion coefficient, distribution factor, aperture size same as reported in Tables 2 and 3. The fracture aperture is varied from 0.0000005 to 0.0005 m and is presented in Fig. 4. It is observed from Fig. 4a that when fracture aperture is increased to 0.0005 the final normalized concentrations for different ions (Cl⁻, F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺) are increased by 0.77, 0.96, 1.11, 2.12, 0.36 and 0.05%. From Fig. 4b, it is observed that when aperture is reduced to 0.000005 m, and the normalized concentrations for different ions (Cl⁻, F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺) are reduced by 2.72, 3.8, 4.6, 10.8, 7 and 16%; and when the aperture is further reduced to 0.0000005 m as presented in Fig. 4c, the final normalized concentrations for different ions (Cl⁻, F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺) are reduced by 4.7, 6.8, 8.3, 16.5, 11.4 and 26.8%. This indicates that concentration of reactive ions reduces when fracture aperture is reduced. Similar results were reported by Grisak and Pickens (1980) and Satavalekar (2015).

Fig. 4

Effect of fracture aperture on concentration

5 Conclusions

The one-dimensional two-coupled formulation for the contaminant transport through fracture and matrix can be modelled using EFGM. It is validated with the example from Tang et al. (1981). The size of the support domain (D_max) should be maintained by 1.25 for better results. In the present study, transport of different ions like Cl⁻, F⁻, Na⁺, K⁺, Cu²⁺ and Mg²⁺ has been considered in the fracture, and the behaviour of the same has been presented by performing parametric study. The parameters considered are fracture flow velocity, dispersivity, diffusion coefficient and distribution coefficient, and the following conclusion has been drawn.

• It can be observed that the flow velocity in fracture is responsible for the rate of contaminant transported in the fracture media. It is also observed that the transport is also governed by diffusion coefficient and distribution coefficient of different ions. A non-reactive ion-like Cl⁻ will move faster than Mg2+ ion.

• Fracture aperture plays a similar role like fracture velocity in reducing the concentration in the fracture. The larger the aperture, the larger is the concentration transported in the fracture and vice versa. It is observed that with smaller aperture sizes, reactive ions diffuse more in the matrix and less in the fracture.