Modeling of High-Pressure Fuel Injection in Internal Combustion Engines

Abstract

The internal combustion engine has been a major power plant in transportation and industry, and demands continuously advanced technologies to improve its performance and fuel economy, and to reduce its pollutant emissions. Liquid fuel injection is critical to the combustion process in both compression ignition (CI) diesel engines and gasoline direct injection (GDI) engines. Much effort has been focused on modeling of spray atomization, droplet dynamics, and vaporization using a Lagrangian-drop Eulerian-fluid (LDEF) framework, which has been applied in engine computational fluid dynamic (CFD) simulations with success. However, recent experiments have shown the mixing-controlled characteristics of high-pressure fuel injection under vaporization conditions that are relevant to both gasoline and diesel engines. Under such conditions, instead of being dominated by droplet dynamics, the vaporization process of a liquid spray is limited by the entrainment rate of hot ambient gas and a saturated equilibrium phase is reached within the two-phase region. This suggests that an alternative approach of fuel spray modeling might be applicable. An equilibrium phase (EP) spray model was recently proposed for application to engine combustion simulation, based on this mixing-controlled jet theory and assumption of local phase equilibrium. This model has been applied to simulate both diesel fuel injection and GDI sprays, and has shown excellent predictions for transient vapor/liquid penetrations, spatial distribution of mixture fraction, as well as combustion characteristics in terms of flame lift-off length and soot emission. It has also shown better computational efficiency than the classical LDEF spray modeling approach since the dynamic process of droplet breakup, collision, coalescence, and vaporization is not modeled. The model and results relevant to engine simulation are reviewed in this chapter.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In all direct injection engines, such as diesel and gasoline direct injection (GDI) engines, high-pressure fuel spray is an important process that impacts the subsequent steps of fuel/air mixture preparation, auto-ignition, combustion, emission formation, etc. Multiple-injection strategies with shaped rate-of-injection profile have been used as effective means for reduction of combustion noise (Augustin et al. 1991; Schulte et al. 1989), particulate matter, and nitrogen oxides (NO_x) emissions (Han et al. 1996; Nehmer et al. 1994; Pierpont et al. 1995; Su et al. 1996; Tow et al. 1994). In advanced combustion modes, such as reactivity controlled compression ignition (RCCI) (Reitz et al. 2014) and partially premixed compression ignition (PPCI) (Musculus et al. 2013), the stability and controllability of high-efficient combustion are usually achieved by in-cylinder stratification that is tailored by injection strategies. Although the study of liquid fuel spray has been ongoing for decades in engine combustion research community, it is still required to better understand high-pressure fuel injection process in order to improve engine design and meet ever-stringent regulations. Conventional knowledge suggests that the liquid spray is dominated by dynamic processes of liquid breakup, collision, coalescence, and interfacial vaporization. After exiting the nozzle into the combustion chamber, the continuous liquid phase is disintegrated into discrete liquid structure through aerodynamic force, cavitation, and turbulence effects, which is followed by secondary breakup and drop collision. Finite-rate vaporization occurs when the droplet is surrounded by unsaturated vapor.

In computational fluid dynamics (CFD) studies, the techniques for multi-phase flow problem can be generally divided into two categories: the Eulerian–Eulerian and the Lagrangian–Eulerian approaches. In the Eulerian–Eulerian approach, both gaseous and liquid phases are resolved on a computational mesh as continuous Eulerian fluids. For fuel injection simulations, this Eulerian–Eulerian approach usually demands refined mesh resolution of the order of microns in order to fully resolve the internal and/or near-nozzle region or even to resolve the discrete liquid drops. However, the characterization of a sharp interface between liquid and gas still needs to be modeled, such as volume-of-fluid (VOF) methods, level-set methods, or front-tracking methods (Gueyffier et al. 1999). While it provides detailed insight into the processes of internal flow and external spray development (Battistoni et al. 2018; Lacaze et al. 2012; Ménard et al. 2007; Xue et al. 2015; Yue et al. 2018a), the computational cost of this Eulerian–Eulerian approach is prohibitively expensive for application in large-scale problems, e.g., internal combustion (IC) engine simulations.

The Lagrangian–Eulerian approach has been widely used for engine simulations, wherein the liquid phase is represented as Lagrangian parcels and the gaseous phase is resolved as a continuous Eulerian fluid. Specifically, the liquid fuel is introduced into the computational domain as discrete ‘blobs’ with the prescribed boundary conditions, such as rate of injection, spray cone angle, initial Sauter mean diameter (SMD) (Reitz 1987; Reitz and Diwakar 1987). Following that, the processes of droplet/blob breakup, collisions, coalescence, and vaporization are also modeled (Beale et al. 1999; Munnannur et al. 2009; Ra et al. 2009; Ricart et al. 1997; Som et al. 2010; Su et al. 1996). A hybrid Kelvin–Helmholtz (KH)/Rayleigh–Taylor (RT) instability analysis model is often used to predict drop breakup (Su et al. 1996). In this case, a breakup length determined from Levich’s theory (Levich 1962) is often adopted to regulate the competition between KH and RT breakup (Beale et al. 1999; Ricart et al. 1997). Further development of breakup models has led to the inclusion of in-nozzle flow effects, such as cavitation and turbulence (Som et al. 2010). Recent development also enables the coupling of Lagrangian-drop Eulerian-fluid (LDEF) spray modeling with internal flow simulation (Saha et al. 2017, 2018; Wang et al., 2011b), wherein the prescribed fluid condition at the nozzle outlet is not required and internal flow effects can be directly included. The spray modeling usually involves a number of model constants that requires optimization to improve the prediction. Perini et al. (2016) applied a multi-objective genetic algorithm (GA) to study the interactions of various spray model constants for improved prediction accuracy in simulations of a diesel spray. However, accurately predicting the fuel injection and spray process under a wide range of engine-relevant conditions and for different types of fuel remains a very challenging task.

While much effort has been focused on modeling liquid breakup and droplet vaporization, the experimental study (Siebers 1998, 1999) has revealed the mixing-controlled characteristics of high-pressure fuel injection under diesel engine-relevant conditions. In this scenario, the liquid atomization is strong enough that the liquid jet can be considered analogous to a turbulent gas jet and the vaporization process is limited by the rate of hot ambient gas entrainment, rather than by liquid breakup and mass transfer rates at droplet surfaces. It is assumed that local phase equilibrium is achieved and a saturated vapor condition is fully reached at the tip of the liquid length.

Iyer et al. (2000) performed a diesel spray CFD simulation with a two-fluid model where the Eulerian transport equations are solved for both the liquid and the gaseous phases. In their simulation approach, the vaporization is controlled by turbulent mixing by applying the locally homogeneous flow (LHF) approximation with an empirical phase equilibrium model. The results showed reasonably good agreement in the liquid length prediction, again suggesting the mixing-controlled behavior of diesel sprays. Matheis et al. (2017) adopted a detailed thermodynamic phase equilibrium model (Qiu et al. 2014) that consists of phase stability analysis and flash calculation in large eddy simulation (LES) of the Engine Combustion Network (ECN) Spray A condition and concluded that the mixing-controlled two-phase mixture model can be applied for dense or moderately dense spray regimes.

An efficient equilibrium phase (EP) spray model (Yue and Reitz 2017, 2018) has been recently proposed for engine CFD simulations, which is based on mixing-controlled jet theory and the assumption of local phase equilibrium. This model has been applied to simulate diesel-type fuel injection as well as GDI sprays with good predictions in terms of spray and combustion characteristics under a wide range of operating conditions without the need for model constant tuning. Moreover, the model shows better computational efficiency than the classical spray modeling approach since the consideration of the droplet dynamic processes is bypassed.

In the following section, an idealized model for mixing-controlled sprays and the derivation of a liquid length scaling law are reviewed. Then, the formulation of the EP spray model for CFD simulations and its application to diesel and GDI spray simulations are presented, followed by a brief summary.

2 Mixing-Controlled Vaporization of High-Pressure Sprays

Siebers (1998, 1999) studied liquid fuel penetration in a constant volume chamber operated under diesel-like conditions for a number of fuels, injector orifice sizes, and ambient conditions. This study discovered that: (1) The liquid length, which is defined as the maximum penetration distance of liquid fuel, linearly correlates with injector orifice size; (2) the liquid length is insignificantly dependent on injection pressure. These experimental findings can be well explained by mixing-controlled vaporization process, which is examined by applying jet theory.

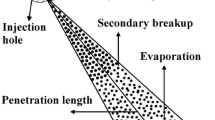
Siebers’ idealized model for high-pressure spray is illustrated in Fig. 5.1, which assumes a quasi-steady flow with a uniform growth rate and perfect adiabatic mixing within the spray boundaries. The dashed lines outline the control volume used for mass, momentum, and energy balances. The downstream side of the control surface ($x = L$, and L is the liquid length) is defined as the axial location where the fuel has just completely vaporized (viz., the liquid length).

Fig. 5.1

Schematic of the ‘idealized’ spray model used to develop the liquid length scaling law (Siebers 1999)

Applying integral analysis for the controlled volume with the assumption of local thermodynamic equilibrium, while neglecting the recovery of the kinetic energy in the fuel vaporization region, the following equations are derived from mass and momentum conservation:

$$ \dot{m}_{f} = \rho_{f} \cdot A_{\text{noz}} \cdot U_{\text{inj}} = \dot{m}_{f} \left( x \right) \propto \rho_{f} \cdot d^{2} \cdot U_{\text{inj}} $$

(5.1)

$$ \dot{m}_{a} \left( x \right) = \rho_{a} \cdot A\left( x \right) \cdot U\left( x \right) \propto \sqrt {\rho_{a} \cdot \rho_{f} } \cdot d \cdot x \cdot U_{\text{inj}} \cdot { \tan }(\theta /2) $$

(5.2)

$$ \dot{m}_{f} \cdot U_{\text{inj}} = \dot{m}_{f} \left( x \right) \cdot U\left( x \right) + \dot{m}_{a} \left( x \right) \cdot U\left( x \right) $$

(5.3)

where $\dot{m}_{f}$ is the injected fuel mass flow rate, $\rho_{f}$ is the injected fuel density, $A_{\text{noz}}$ is the effective nozzle area, $U_{\text{inj}}$ is the constant injection velocity, $\dot{m}_{f} \left( x \right)$ is the fuel mass flow rate at any axial location x, $\dot{m}_{a} \left( x \right)$ is the mass flow rate of entrained ambient gas, $\rho_{a}$ is the ambient gas density, $A\left( x \right)$ is the spray cross-sectional area, $U\left( x \right)$ is the radially uniform spray velocity, d is the nozzle diameter, and $\theta$ is the spray spreading angle.

From jet theory, $\dot{m}_{a} \left( x \right)$ is proportional to d, while $\dot{m}_{f} \left( x \right)$ is proportional to d², which results in a linear dependency of liquid length on the nozzle diameter if the vaporization process is mixing controlled. On the other hand, both $\dot{m}_{a} \left( x \right)$ and $\dot{m}_{f} \left( x \right)$ are proportional to $U_{\text{inj}}$, indicating an independency of liquid length on injection velocity or injection pressure.

Equations (5.1)–(5.3) can be rearranged to give a parabolic equation for the fuel/ambient gas ratio, $\frac{{\dot{m}_{f} \left( x \right)}}{{\dot{m}_{a} \left( x \right)}}$, and its positive root gives the axial variation of this ratio,

$$ \frac{{\dot{m}_{f} \left( x \right)}}{{\dot{m}_{a} \left( x \right)}} = \frac{2}{{\sqrt {1 + 16 \cdot \tilde{x}^{2} } - 1}} $$

(5.4)

Here, $\tilde{x} = x/x^{ + }$ is the axial distance in the spray normalized by $x^{ + } = \sqrt {\frac{{\rho_{f} }}{{\rho_{a} }}} \cdot \frac{{\sqrt {C_{a} } \cdot d}}{{{ \tan }\left( {\theta /2} \right)}}$. $C_{a}$ is the area-contraction coefficient of nozzle.

At the tip of the liquid length ($x = L$), the liquid fuel has just vaporized completely such that

$$ \frac{{\dot{m}_{f} \left( L \right)}}{{\dot{m}_{a} \left( L \right)}} = B\left( {T_{a} ,P_{a} ,T_{f} } \right) $$

(5.5)

The term $B\left( {T_{a} ,P_{a} ,T_{f} } \right)$ is the mass ratio of liquid fuel and ambient gas in a completely vaporized and saturated condition, which is a thermodynamic equilibrium problem with given ambient temperature $\left( {T_{a} } \right)$, pressure $\left( {P_{a} } \right)$, and injected fuel temperature $\left( {T_{f} } \right)$.

A liquid length scaling law (Siebers 1999) is then derived by combining Eqs. (5.4) and (5.5) and substituting the definition of $x^{ + }$,

$$ L = C_{L} \cdot \sqrt {\frac{{\rho_{f} }}{{\rho_{a} }}} \cdot \frac{{\sqrt {C_{a} } \cdot d}}{{{ \tan }\left( {\theta /2} \right)}}\sqrt {\left( {\frac{2}{{B\left( {T_{a} ,P_{a} ,T_{f} } \right)}} + 1} \right)^{2} - 1} $$

(5.6)

Here, $C_{L}$ is a model constant which has a theoretical value of 0.38. Siebers adjusted this value to 0.62 to match n-hexadecane and heptamethylnonane liquid length data. The adjusted value of 0.62 is also used in current work.

Siebers (1999) compared the scaling law with measured liquid length data for several types of fuels under a very wide range of engine-relevant operating conditions and showed that the scaling law reproduced all major trends in the experimental results. The close agreement between the liquid length scaling law and the measured data suggests that vaporization in a high-pressure diesel injection approaches a limit governed by spray mixing processes, and atomization and local interphase transport processes at droplet surfaces are not limiting factors for fuel vaporization. Parrish (2014) examined the scaling law in GDI measurement by lumping the term $C_{\text{L}} \cdot \frac{{\sqrt {C_{a} } \cdot d}}{{{ \tan }\left( {\theta /2} \right)}}$ into a single constant, which was adjusted through trial and error to match the experimental data. It was found that the lumped constant reached a fixed value at high ambient temperature, indicating that under such conditions the fuel vaporization also becomes mixing controlled in GDI sprays.

3 Equilibrium Phase (EP) Spray Model

3.1 Governing Equations

In the LDEF approach for two-phase turbulent flow simulations, such as in the KIVA code (Amsden et al. 1989) implementation, the liquid flow and gaseous flow are resolved on two different but connected fields. The gaseous mixture of ambient gas and vaporized fuel is resolved on an Eulerian field where the transport equations are solved for species, momentum, and internal energy. Using the Reynolds-averaged Navier–Stokes (RANS) method, the instantaneous equations are averaged and expressed with mean quantities, as shown below (Amsden et al. 1989).

The continuity equation for species m is

$$ \frac{{\partial \rho_{m} }}{\partial t} + \nabla \cdot \left( {\rho_{m} {\mathbf{u}}} \right) = \nabla \cdot \left( {\rho D\nabla \left( {\frac{{\rho_{m} }}{\rho }} \right)} \right) + \dot{\rho }_{m}^{c} + \dot{\rho }_{m}^{s} \delta_{m1} $$

(5.7)

where ${\mathbf{u}}$ is the velocity vector for the mean flow, $\rho_{m}$ is the mass density of species m, $\rho$ is the total mass density, D is the diffusion coefficient, $\dot{\rho }_{m}^{c}$ is a source term due to chemical reactions, $\dot{\rho }_{m}^{s}$ is a source term due to the spray, and $\delta_{m1}$ is the Dirac delta function so that there is no spray source term for non-fuel species.

The momentum equation for the fluid mixture is

$$ \frac{{\partial \left( {\rho {\mathbf{u}}} \right)}}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{uu}}} \right) + \nabla P = \mu \nabla \cdot \left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{\text{T}} - \frac{2}{3}\nabla \cdot {\mathbf{uI}}} \right) - \nabla \left( {\frac{2}{3}\uprho{\text{k}}} \right) + F^{s} $$

(5.8)

where P is the fluid pressure, $\mu$ is the dynamic viscosity, superscript T denotes transpose, ${\mathbf{I}}$ is the identity tensor, k is the turbulent kinetic energy, and $F^{s}$ is the momentum exchange between the liquid spray and the ambient flow.

The internal energy equation is

$$ \frac{{\partial \left( {\rho I} \right)}}{\partial t} + \nabla \cdot \left( {\rho {\mathbf{u}}I} \right) = - P\nabla \cdot {\mathbf{u}} + \lambda \nabla^{2} T + \rho D\sum\limits_{m} {\left( {h_{m} \nabla^{2} \left( {\frac{{\rho_{m} }}{\rho }} \right)} \right)} + \rho \varepsilon + \dot{Q}^{c} + \dot{Q}^{s} $$

(5.9)

where I is the specific internal energy, $\lambda$ is the thermal conductivity, $h_{m}$ is the specific enthalpy of species m, $\varepsilon$ is the dissipation rate of turbulent kinetic energy, $\dot{Q}^{c}$ is a source term due to chemical heat release, and $\dot{Q}^{s}$ is a source term due to spray interaction.

For a turbulent flow, the Reynolds stresses are modeled by assuming the same form as the viscous tensor for Newtonian fluids but with a modified viscosity, $\mu$, which is given as

$$ \mu = \mu_{0} + \mu_{t} $$

(5.10)

where $\mu_{0}$ is the laminar dynamic viscosity, $\mu_{t} = C_{\mu } k^{2} /\varepsilon$ is the turbulent viscosity, and $C_{\mu }$ is a model constant. Turbulent fluxes of species and enthalpy are modeled by assuming Fick’s law diffusion with a single diffusion coefficient, which is given as

$$ D = \frac{\mu }{\rho \cdot Sc} $$

(5.11)

where $Sc$ is the Schmidt number and a constant value is assumed. Two more transport equations for k and $\varepsilon$ are needed in the turbulence model (Han et al. 1995; Launder et al. 1972; Wang et al. 2011a; Yakhot et al. 1992), which will be discussed later in this section.

On the other hand, the liquid fuel is initialized at the location of nozzle exit as Lagrangian parcels with the prescribed rate of injection and initial size equal to an effective nozzle diameter. Each parcel represents an assembly of a number of identical drops with the same temperature, size, momentum, etc. The Lagrangian and Eulerian fluids interact with each other in terms of mass, momentum, and energy transfer, through the source terms $\dot{\rho }_{m}^{s} ,F^{s} ,\dot{Q}^{s}$ introduced above. In the traditional LDEF approach, the two-phase flow process is primarily governed by the dynamics of the Lagrangian drops, i.e., breakup, collision, and vaporization.

In order to model the fuel spray process with emphasis on mixing-controlled vaporization, it is desired to simulate the liquid as a continuous fluid with an Eulerian treatment. However, this treatment requires the computational mesh to be refined to a micron level such that the near-nozzle flow can be resolved, and its application in engine simulations is limited due to the resulting significant computational cost. In the current EP model, the framework of the LDEF approach is retained such that a practical mesh resolution can be used for engine simulations. However, the non-equilibrium processes of liquid breakup and collision are not considered. Instead, after being injected into the domain, the Lagrangian parcels gradually transition to the Eulerian liquid phase, which is assumed to be homogenously mixed with the local gaseous phase. The governing equation for the Eulerian liquid can be written as

$$ \frac{{\partial \rho_{l} }}{\partial t} + \nabla \cdot \left( {\rho_{l} {\mathbf{u}}} \right) = \nabla \cdot \left[ {\rho D\nabla \left( {\frac{{\rho_{l} }}{\rho }} \right)} \right] + \dot{S}_{\text{EP}} + \dot{S}_{\text{release}} $$

(5.12)

where the subscript l denotes the Eulerian liquid phase, $\dot{S}_{E}$ describes the mass exchange between the Eulerian liquid and vapor phase assuming phase equilibrium, and $\dot{S}_{\text{release}}$ is the source term that describes the transition rate from Lagrangian drops to the Eulerian liquid. Other governing equations used in the LDEF approach are unchanged, and the Eulerian liquid can be considered as an intermediate step between Lagrangian drops and Eulerian vapor.

Figure 5.2 illustrates a schematic diagram for the current spray modeling approach. The injected Lagrangian parcels are denoted by the yellow spheres with size proportional to the drop mass. The blue contour represents the Eulerian liquid mass fraction, while the red contour represents the vapor mass fraction. The dashed arrows indicate velocity vectors of the Eulerian flow field. As can be seen, the droplets release mass smoothly as they move away from the nozzle. The phase change for the Eulerian fluid $\left( {\dot{S}_{\text{EP}} } \right)$ is solved for by employing a phase equilibrium solver, and it is a function of the local mixture composition and thermodynamic state. Thus, the process of fuel vaporization becomes controlled by the air entrainment and mixing, as illustrated by the velocity field.

Fig. 5.2

Schematic of EP spray model, generated from CFD results (Yue et al. 2017)

A liquid-jet model was derived based on Siebers’ scaling analysis to solve for the term $\dot{S}_{\text{release}}$ in Eq. (5.12). Combining Eqs. (5.1) and (5.4) gives

$$ \gamma \left( x \right) = \frac{{\dot{m}_{a} \left( x \right)}}{{\dot{m}_{a} \left( L \right)}} = \frac{{\sqrt {1 + 16\tilde{x}^{2} } - 1}}{{\sqrt {1 + 16\left( {L/x^{ + } } \right)^{2} } - 1}} $$

(5.13)

The function $\gamma \left( x \right)$ is the ratio between the entrainment flow rate at distance x and the one at the tip of liquid length. In a mixing-controlled spray, $\gamma \left( x \right)$ also represents the possible upper bound of the proportion of fuel being vaporized at any axial location. Therefore, the conversion rate from the Lagrangian parcels to the Eulerian liquid is modeled by adopting the function $\gamma \left( x \right)$ as

$$ \dot{S}_{\text{release}} = \left( {m_{\text{parcel}} - m_{\text{parcel,initial}} \cdot \left( {1 - \gamma \left( x \right)} \right)} \right)/{\text{d}}t $$

(5.14)

Here, $m_{\text{parcel}}$ is the mass of the parcel, $m_{\text{parcel,initial}}$ is the initial mass of the same parcel upon injection, and dt is the computational time step. One should note that $\dot{S}_{\text{release}}$ controls only the process of liquid release from Lagrangian-to-Eulerian phase and not the vaporization process. The vaporization process is controlled by the local phase equilibrium $\left( {\dot{S}_{\text{EP}} } \right)$.

The spray spreading angle $\theta$ is modeled as a function of gas/liquid density ratio, $\frac{{\rho_{f} }}{{\rho_{a} }}$, Reynolds number, $Re_{f}$, and Weber number, $We_{f}$, according to the aerodynamic surface wave theory for liquid-jet breakup (Ranz 1958; Reitz et al. 1979):

$$ \tan \theta /2 = C_{\theta } 4\pi \sqrt {\frac{{\rho_{a} }}{{\rho_{f} }}} f\left( {\frac{{\rho_{f} }}{{\rho_{a} }}\left( {\frac{{Re_{f} }}{{We_{f} }}} \right)^{2} } \right) $$

(5.15)

$C_{\theta }$ is a model constant and is dependent on injector’s internal geometry and flow condition. The function, f, is given in the references. The value of $C_{\theta }$ can be determined from the best fit of the experimental data. Figure 5.3 shows a comparison of experiments and model predictions of spreading angles as a function of injection pressure for three ambient densities, for the ECN Spray A injector, with a $C_{\theta }$ of 0.45.

Fig. 5.3

Spray spreading angle as a function of injection pressure at three ambient conditions (Yue et al. 2017)

3.2 Gas-Jet Model

The Lagrangian and Eulerian fluids are fully coupled in conservation of mass, momentum, and energy. An aerodynamic drag force, $F^{s}$, is applied to the Lagrangian parcels when a relative velocity exists between the liquid droplets and the gaseous phase, and leads to momentum transfer as seen in the momentum equation. $F^{s}$ is modeled as

$$ F^{s} = \frac{3}{8}\frac{\rho }{{\rho_{f} }}\frac{{\left| {{\mathbf{u}} + {\mathbf{v}}^{{\prime }} - {\mathbf{v}}} \right|}}{{r_{d} }}\left( {{\mathbf{u}} + {\mathbf{v}}^{{\prime }} - {\mathbf{v}}} \right)C_{D} C_{\text{distortion}} $$

(5.16)

where v is the velocity vector of droplet, ${\mathbf{v}}^{{\prime }}$ is a turbulent drop dispersion velocity, and $r_{d}$ is the droplet radius. The effect of droplet distortion on drag is considered by an enhanced coefficient, $C_{\text{distortion}}$ (Liu et al. 1993). The drag coefficient for undistorted droplet, $C_{D}$, is modeled as

$$ C_{D} = \left\{ {\begin{array}{*{20}l} {\frac{24}{{Re_{d} }}\left( {1 + 1/6Re_{d}^{2/3} } \right) } \hfill & {Re_{d} < 1000} \hfill \\ {0.424 } \hfill & {Re_{d} \ge 1000} \hfill \\ \end{array} } \right.,\quad Re_{d} = \frac{{2\rho \left| {{\mathbf{u}} + {\mathbf{v}}^{{\prime }} - {\mathbf{v}}} \right|r_{d} }}{{\mu_{t} }} $$

(5.17)

However, a practical computational mesh for engine simulation is usually much larger than the injector orifice size and cannot resolve the velocity profile in the near-nozzle region. The estimation of drag force and momentum exchange becomes dependent on mesh size when a mean value of CFD-resolved velocity is used to calculate the relative velocity, and a coarse mesh usually results in overprediction of momentum transfer and slow spray penetration. In order to improve the grid independency of momentum coupling, the gas-jet model (Abani et al. 2008a, b) is employed, wherein a sub-grid scale velocity ${\mathbf{u}}_{sgs}$ estimated from the turbulent gas-jet theory is used instead of the CFD-resolved velocity.

In the gas-jet model, the solution for a gas jet with same injection velocity, mass flow rate, and injection momentum is used to represent the velocity field of the liquid fuel spray. Accordingly, an equivalent orifice size for the gas jet is determined to be $d_{\text{eq}} = d\sqrt {\rho_{f} /\rho }$. In a gas jet with transient injection profile, the effective injection velocity ${\mathbf{u}}_{\text{eff}} \left( {x,t} \right)$ can be written as a function of axial distance, x, and time, t, which represents the convolution of n successive changes in the initial injection velocity, ${\mathbf{U}}_{\text{inj}} \left( {t_{0} } \right)$ (Abani et al. 2007),

$$ {\mathbf{u}}_{\text{eff}} \left( {x,t} \right) = {\mathbf{U}}_{\text{inj}} \left( {t_{0} } \right) + \sum\limits_{k = 1}^{n} {\left( {\left( {1 - { \exp }\left( { - \frac{{t - t_{k} }}{{\tau \left( {x,t_{k} } \right)}}} \right)} \right) \times \left( {{\mathbf{U}}_{\text{inj}} \left( {t_{k} } \right) - {\mathbf{U}}_{\text{inj}} \left( {t_{k - 1} } \right)} \right)} \right)} $$

(5.18)

$$ \tau \left( {x,t} \right) = St\frac{x}{{\left| {{\mathbf{U}}_{\text{inj}} \left( t \right)} \right|}} $$

(5.19)

Here, the jet response time, $\tau \left( {x,t} \right)$, is calculated using the spray jet analogy with a constant value of 3.0 for the particle Stokes number, $St$ (Abani et al. 2007).

Once the effective injection velocity is determined, the transient sub-grid gas-jet velocity can be calculated with given axial distance, radial distance, and time, as shown in Eqs. (5.20)–(5.23) (Perini et al. 2016).

$$ {\mathbf{u}}_{\text{sgs}} \left( {x,r,t} \right) = \frac{{f\left( \chi \right){\mathbf{u}}_{\text{eff}} \left( {x,t} \right)}}{{\left( {1 + \frac{{12r^{2} }}{{K_{\text{entr}}^{2} x^{2} }}} \right)^{2} }} $$

(5.20)

$$ f\left( \chi \right) = \left\{ {\begin{array}{*{20}l} {1/\chi , } \hfill & {\chi \ge \varphi } \hfill \\ {\gamma_{ \hbox{max} } - \frac{{32\gamma_{ \hbox{max} }^{3} \left( {\chi - 1} \right)^{2} }}{{\left( {3 + \Delta } \right)^{2} \left( {3 + \Delta - 4\gamma_{ \hbox{max} } } \right)}}, } \hfill & {1 \le \chi < \varphi } \hfill \\ {\gamma_{ \hbox{min} } + \chi \left( {2 - \chi } \right)\left( {\gamma_{ \hbox{max} } - \gamma_{ \hbox{min} } } \right),} \hfill & {\chi < 1} \hfill \\ \end{array} } \right.;\quad \chi = \frac{{xK_{\text{entr}} }}{{3d_{\text{eq}} }} $$

(5.21)

$$ \Delta = \sqrt {9 - 8\gamma_{ \hbox{max} } } $$

(5.22)

$$ \varphi = \frac{3 + \Delta }{{4\gamma_{ \hbox{max} } }} $$

(5.23)

The denominator in the right-hand side of Eq. (5.20) describes the velocity decay along radial direction, and $K_{\text{entr}}$ is a coefficient of turbulent entrainment rate. The piecewise function, $f\left( \chi \right)$, describes the velocity damping profile along axial direction that is defined by $\gamma_{ \hbox{max} }$ and $\gamma_{ \hbox{min} }$. The values of these model constants are adopted from a multi-objective GA optimization in simulation of diesel spray (Perini et al. 2016).

3.3 Phase Equilibrium in High-Pressure Sprays

Liquid fuel injection involves several non-equilibrium phenomena. However, as discussed previously, liquid vaporization is limited by the rate of ambient hot gas entrainment, while local interphase transport rates are so fast due to the small drop sizes that the assumption of local phase equilibrium can be applied to simplify the problem. Therefore, other than the liquid fuel and ambient gas mixing rate, the determination of phase equilibrium is also critical for the determination of spray vaporization.

For a multi-component mixture under ideal conditions, the vapor/liquid equilibrium can be determined using Raoult’s law,

$$ P_{i,v} = X_{i,l} \cdot P_{{{\text{sat}},i}} $$

(5.24)

$P_{i,v}$ is the partial pressure of species i in the vapor phase. $X_{i,l}$ is the mole fraction in the liquid phase. $P_{{{\text{sat}},i}}$ is the vapor pressure of the pure species for a given temperature, which can be calculated by a number of vapor pressure equations (Reid et al. 1987). The subscripts v and l denote the vapor phase and liquid phase, respectively. It is seen that equilibrium in this case only depends on temperature. However, under high-pressure conditions, Raoult’s law is no longer valid, and a real gas equation of state (EoS) is needed to solve the problem.

The Gibbs free energy is a thermodynamic potential that is used to measure the obtainable energy from a closed thermodynamic system, and it is minimized when the equilibrium is reached with a specified temperature, pressure, and mixture composition. Therefore, the equilibrium calculation is a search for the global minimum of the Gibbs free energy in a multi-dimensional space, which is usually achieved by requiring fugacity equality, e.g., in case of a two-phase equilibrium,

$$ f_{i,v} = f_{i,l} $$

(5.25)

f is the fugacity, which is equal to the pressure of an ideal gas that has the same chemical potential as the real gas at some pressure. However, the fugacity equality is a necessary but insufficient condition for phase equilibrium, because it stands for a local stationary point that does not guarantee a global minimum. While the local extreme given by the fugacity equality could happen to be the global extreme for a simple fluid, this approach sometimes presents a ‘false’ equilibrium state for a multi-component mixture.

Qiu and Reitz (2014a, b, 2015), Qiu et al. (2014) developed a phase equilibrium solver based on classical thermodynamic equilibrium with a real gas EoS, which is reported to be thermodynamically consistent and is computationally robust and efficient. This solver has been applied to a number of multi-phase flow problems such as condensation and supercritical fluids. In this approach, the phase equilibrium problem is solved in two steps, viz., a phase stability test and a phase-splitting calculation. The phase stability test is performed first to examine whether a phase-splitting calculation is required and to provide initial guess values for the phase-splitting calculation. For a multi-component mixture, the tangent plane distance (TPD) method (Baker et al. 1982; Michelsen 1982) is used to test the phase stability. The TPD function is defined as:

$$ {\text{TPD}}\left( \varvec{X} \right) = \sum\limits_{i = 1}^{{N_{c} }} {X_{i} \left( {\mu_{i} \left( \varvec{X} \right) - \mu_{i} \left( \varvec{Z} \right)} \right)} $$

(5.26)

Here, X is the mole fraction array, Z is the feeding composition array, $\mu$ is the chemical potential, and $N_{c}$ is the number of components. Geometrically, ${\text{TPD}}\left( \varvec{X} \right)$ represents the vertical distance from the tangent hyperplane to the molar Gibbs free energy surface of Z. It requires ${\text{TPD}}\left( \varvec{X} \right)$ to be nonnegative at all stationary points to achieve phase stability. Therefore, the TPD method reduces the search space from the whole domain to the local extremes and hence an exhaustive search of all possible $\varvec{X}$ is avoided. Whenever the phase stability test yields a negative value of ${\text{TPD}}\left( \varvec{X} \right)$, the flash calculation is performed based on the Rachford–Rice algorithm (Rachford et al. 1952):

$$ \sum\nolimits_{i = 1}^{{N_{c} }} {\frac{{Z_{i} \left( {k_{i} - 1} \right)}}{{1 + \lambda \left( {k_{i} - 1} \right)}} = 0} $$

(5.27)

$k_{i}$ is the phase equilibrium ratio of species i, and $\lambda$ is the mole fraction of one phase. The outcome of the stability test is used as an initial guess for solving the objective function.

3.4 Equation of State

In CFD simulations, the EoS calculation is called numerous times for each computational cell at each time step. Therefore, it is important to maintain a good balance between accuracy and efficiency for EoS calculation in engineering applications. The Peng–Robinson (PR) EoS is a two-parameter efficient cubic EoS, which has the form

$$ P = R_{u} T/\left( {\bar{v} - b_{m} } \right) - a_{m} /\left( {\bar{v}^{2} + 2b_{m} \bar{v} - b_{m}^{2} } \right) $$

(5.28)

where P is the pressure, T is the temperature,$\bar{v}$ is the molar volume, and $R_{u}$ is the universal gas constant. $a_{m}$ and $b_{m}$ are attraction and repulsion parameters, respectively. For species i, the parameters are expressed as functions of critical properties and acentric factor,

$$ {\text{a}}_{i} = 0.45724R_{u}^{2} T_{c}^{2} /P_{c}^{2} \left[ {1 + f\left( \omega \right)\left( {1 - \sqrt {T_{c} /T} } \right)} \right]^{2} $$

(5.29)

$$ {\text{b}}_{i} = 0.07780R_{u} T_{c} /P_{c} $$

(5.30)

where P_c is the critical pressure, T_c is the critical temperature, $\omega$ is the acentric factor, and $f\left( \omega \right) = 0.37464 + 1.54226\omega - 0.26992\omega^{2}$. The parameters for a multi-component mixture can be calculated following the van der Waals mixing rule

$$ a_{m} = \sum\limits_{i} {\sum\limits_{j} {x_{i} x_{j} \left( {a_{i} a_{j} } \right)^{{\frac{1}{2}}} \left( {1 - k_{ij} } \right)} } $$

(5.31)

$$ b_{m} = \sum\limits_{i} {x_{i} b_{i} } $$

(5.32)

The subscript m denotes the mixture, and i and j denote individual species. x is the species mole fraction. $k_{ij}$ is the binary interaction parameter for species i and j, and its value can be found in reference (Knapp 1982). Table 5.1 lists the properties required for EoS calculation for the major species that is considered in this work. The listed species in total account for more than 99% mole fraction of the mixtures in either a non-reacting or a reacting case in current study and, therefore, are considered sufficient to represent the complete mixture in the EoS calculations. These parameters are also used by the phase equilibrium solver.

Table 5.1 Species and properties considered for the EoS calculation

Substituting the definition of the compressibility factor ${\text{z}}\mathop {\text{def}}\limits_{ = } P\bar{v}/R_{u} T$ into Eq. (5.28), an alternative form of PR EoS is derived,

$$ z^{3} - \left( {1 - B} \right)z^{2} + \left( {A - 3B^{2} - 2B} \right)z - \left( {AB - B^{2} - B^{3} } \right) = 0 $$

(5.33)

where ${\text{A}} = \frac{{a_{m} P}}{{R_{u}^{2} T^{2} }}$ and ${\text{B}} = \frac{{b_{m} P}}{{R_{u} T}}$. This cubic equation is numerically solved with Newton’s method to yield one or three roots depending on the number of phases.

The internal energy is only a function of temperature when the ideal gas law is applied. When a real fluid is considered at high temperatures and pressures, it requires two independent thermodynamic variables to calculate the non-ideal departure in internal energy. For example, internal energy as a function of temperature and molar volume is expressed as

$$ {\text{I}}\left( {{\text{T}},\bar{v}} \right) = I\left( {T,\infty } \right) + \left( {\frac{{a_{m} - T\frac{{da_{m} }}{dT}}}{{w_{\text{avg}} 2\sqrt 2 b_{m} }}} \right)\left[ {\ln \left| {\frac{{b_{m} \left( {\sqrt 2 - 1} \right) - \bar{v}}}{{b_{m} \left( {\sqrt 2 + 1} \right) + \bar{v}}}} \right|} \right] $$

(5.34)

where $w_{\text{avg}}$ is the mixture-averaged molecular weight. The first term, $I\left( {T,\infty } \right)$, on the right-hand side represents the internal energy at the ideal condition where the molar volume approaches infinity. The second term on the right-hand side represents the departure from ideality. This form of internal energy equation can be solved analytically and is therefore implemented in this study.

Figure 5.4 shows the compressibility factors for a simple fluid ($\omega = 0$) calculated by the PR EoS, in comparison with results by the Lee–Kesler-modified Benedict–Webb–Rubin (BWR) EoS (Reid et al. 1987). The BWR EoS is considered a more accurate EoS that applies to a wide range of pressures and temperatures, but is more computationally expensive compared to the cubic PR EoS. The compressibility factor is plotted as a function of reduced temperature $T_{r}$ and reduced pressure $P_{r}$, which are defined as $T_{r} = T/T_{c}$ and $P_{r} = P/P_{c}$, respectively. A close agreement of predictions by the PR and the BWR EoS can be found at low-reduced pressures with a relative difference less than 5%. The discrepancy increases at higher-reduced pressures, especially at lower-reduced temperatures. The blue symbols in Fig. 5.4 mark the status of major species of engine charge at 900 K, 75 bar, which is relevant to engine operating conditions. It is seen that these species locate in a low-reduced pressure and high-reduced temperature region, where the PR EoS provides similar accuracy as the BWR EoS.

Fig. 5.4

Compressibility factor as a function of reduced pressure and temperature for a simple fluid comparing PR EoS and BWR EoS (Yue et al. 2018b). Black solid lines are BWR EoS, and red dashed lines are PR EoS. The blue symbols are the compressibility factors for selected species at typical engine operating condition (900 K, 75 bar), estimated using this z-chart

The Peng–Robinson EoS was implemented into the KIVA-3vr2 code (Amsden 1999) with the RANS framework, wherein the turbulent viscosity and diffusivity are modeled to provide closures for the Reynolds stresses and turbulent fluxes, respectively. Non-ideal effects in the transport properties are not taken into account here since turbulent transport properties in RANS approach are generally two orders of magnitude larger than laminar transport properties for the turbulent flows in engines.

In the KIVA code, the Navier–Stokes equations are solved by the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) algorithm. Briefly, a corrected pressure $P^{c}$ is yielded to eliminate the difference between $V^{p}$, the predicted volume based on EoS calculation, and $V^{c}$, the corrected volume related to the cell-face velocities (Amsden et al. 1989). This process iterates until the predicted and corrected values converge. Use of a real gas EoS generally requires more iterations since the pressure dependency of thermodynamic derivatives leads to slower convergence compared to the standard KIVA. Therefore, the computational time for an engine CFD simulation is increased by 20–50% when the PR EoS is used (Yue et al. 2018b).

3.5 Generalized RNG Model

For turbulence modeling in engine simulations, the RANS approach is currently the most practical and dominant method because of its computational efficiency. In the RANS approach, two more transport equations for the turbulent kinetic energy, $k$, and its dissipation rate, $\varepsilon$, are solved in addition to the mass, momentum, and energy equations. In this work, a generalized renormalization group (gRNG) k-ε model (Wang et al. 2011a) is used. Compared to the standard two equation models (Launder et al. 1972), the original RNG model (Yakhot et al. 1992) and the modified RNG model (Han et al. 1995), the gRNG model accounts for flow compressibility and has model coefficients that are functions of the flow strain rate. This allows improved predictions in the three types of pure compression of interest in engine flows: a 1D unidirectional axial compression, a 2D cylindrical-radial compression (squish flow), and a 3D spherical compression. In the gRNG model, the transport equations for k and $\varepsilon$ are solved as follows

$$ \rho \frac{Dk}{Dt} = P_{k} - \rho \varepsilon + \dot{W}^{s} + \nabla \cdot \left[ {\alpha_{k} \rho \nu \nabla {\text{k}}} \right] $$

(5.35)

$$ \begin{aligned} \rho \frac{D\varepsilon }{Dt} & = \frac{\varepsilon }{k}C_{1} P_{k} + C_{1}^{ '} \rho \nu \frac{\varepsilon }{k}\left( {\nabla \cdot {\mathbf{u}}} \right)^{2} - C_{2n} \rho \frac{{\varepsilon^{2} }}{k} - \rho R + C_{3} \rho \varepsilon \left( {\nabla \cdot {\mathbf{u}}} \right) \\ & \quad + C_{s} \frac{\varepsilon }{k}\dot{W}^{s} + \nabla \cdot \left[ {\alpha_{\varepsilon } \rho \nu \nabla\upvarepsilon} \right] \\ \end{aligned} $$

(5.36)

where $\dot{W}^{s}$ is a source term due to interactions with the spray (Amsden 1999). v is the kinematic viscosity. The production of turbulent kinetic energy $P_{k}$ and the additional term R from RNG analysis are modeled as

$$ P_{k} = \frac{2}{3}\left[ {a\rho \nu \left( {\nabla \cdot {\mathbf{u}}} \right)^{2} - \rho k\left( {\nabla \cdot {\mathbf{u}}} \right)} \right] $$

(5.37)

$$ R = \sqrt {\frac{{2\left( {1 + a} \right)}}{3}} C_{\mu } C_{\eta } \eta \varepsilon \left| {\nabla \cdot {\mathbf{u}}} \right| $$

(5.38)

The model coefficients are summarized in Table 5.2 (Wang et al. 2011a). $\eta = Sk/\varepsilon$ is the ratio of turbulent to mean strain-time scale, and $S = \left( {2S_{ij} S_{ij} } \right)^{1/2}$ is the magnitude of the mean strain $S_{ij} = \frac{1}{2}\left( {\partial u_{i} /\partial x_{j} + \partial u_{j} /\partial x_{i} } \right)$. The terms a and n reflect the ‘dimensionality’ of the strain rate field, which are defined as

Table 5.2 Coefficients for gRNG turbulence model

$$ a = 3\left( {S_{11}^{2} + S_{22}^{2} + S_{33}^{2} } \right)/\left( {\left| {S_{11} } \right| + \left| {S_{22} } \right| + \left| {S_{33} } \right|} \right)^{2} - 1 $$

(5.39)

$$ n = 3 - \sqrt {2a} $$

(5.40)

4 Diesel Spray Simulation

4.1 ECN Spray A

The Sandia combustion vessel (Pickett et al. 2010, 2011; Skeen et al. 2016) simulates a wide range of ambient environments (temperature, density, oxygen concentration, etc.) for high-pressure fuel injection and provides full optical access to help in the understanding of the details of the spray combustion process. The present spray model is validated with the ECN ‘Spray A’ operating conditions in this section. The Spray A features a single-hole injector. The injected fuel is n-dodecane, which is often used as a surrogate for diesel fuel in research. The injection pressure is 150 MPa, and the fuel temperature is 373 K. The injection profile has a rapid start and end with a steady period in between, forming a top hat profile. For the simulations, the rates of injection were determined by a virtual injection rate generator (http://www.cmt.upv.es/ECN03.aspx), as recommended by the ECN. The specifications of the operating conditions are given in Table 5.3.

Table 5.3 Operating conditions and injector specification for ECN Spray A (Pickett et al. 2010, 2011; Skeen et al. 2016)

As can be seen, cases 1–6 represent non-reacting conditions with 0% oxygen, where the transient liquid/vapor penetration and quasi-steady-state mixture fraction were measured. Mie-scatter and Schlieren imaging were used to track the liquid spray and vapor plume, respectively. Rayleigh-scatter imaging was used for the quantitative measurement of vapor mixture fraction (Pickett et al. 2011). Cases 7–11 represent combusting spray conditions with varying oxygen content and ambient temperature. Laser-induced incandescence (LII) imaging combined with line-of-sight extinction technique was applied for the quantitative measurement of soot volume fraction distribution (Idicheria et al. 2005; Manin et al. 2013; Skeen et al. 2016), while OH chemiluminescence was used to indicate the jet lift-off length (Higgins et al. 2001). In the CFD simulation results, the liquid and vapor phase penetrations are determined as the maximum axial distance between the injector exit and the farthest location with 0.1% liquid volume fraction and with 0.1% vapor mass fraction, respectively. The nearest axial location where the local OH mass fraction reaches 2% of its maximum value is used as the lift-off length. The model constants were kept unchanged for all simulations in this section, as summarized in Table 5.4. For the reacting conditions, the combustion is modeled as a well-stirred reactor. A reduced n-dodecane mechanism (Wang et al. 2014) with 100 species and 432 reactions is used. A reduced mechanism for polycyclic aromatic hydrocarbons (PAHs) is included, which enables the use of a semi-detailed soot model (Vishwanathan et al. 2010) that uses pyrene as soot precursor, and also considers acetylene- and PAHs-assisted surface growth, particle coagulation, and soot oxidation by oxygen and OH.

Table 5.4 Spray model constants

4.2 Grid Sensitivity

Three computational meshes with different resolutions were used so that the grid sensitivity of the spray model could be tested. The three meshes are: Fig. 5.5a—a 2D cylindrical mesh with a refined resolution of 0.7 mm * 0.7 mm * 0.5° at the nozzle; Fig. 5.5b—a 3D cubic mesh with a refined resolution of 1 mm * 1 mm * 1 mm at the nozzle; and Fig. 5.5c—a 3D cubic mesh with a refined resolution of 1.5 mm * 1.5 mm * 1.5 mm at the nozzle. The 2D cylindrical mesh considers a cylindrical computational domain with a radius of 6.332 cm and a height of 10 cm, which is similar to the geometry of the combustion vessel in the experiments. The 3D cubic meshes consider a domain with a width of 1.8 cm and a height of 10 cm, which is large enough to simulate the spray process.

Fig. 5.5

Computational meshes for spray A

Figures 5.6 and 5.7 show transient liquid and vapor penetrations and quasi-steady-state mixture fraction distributions for 900 K, 22.8 kg/m³ and 1100 K, 15.2 kg/m³ operating conditions. The black lines represent the ensemble average of the experimental measurement, and the shadow area indicates the standard deviation. The red, green, and blue lines are CFD predictions with resolutions of 0.7, 1, and 1.5 mm, respectively. Due to the improved grid independency by using liquid-jet and gas-jet models, the liquid penetration is seen to be almost unaffected by the different mesh sizes. However, deviations are found in the vapor penetrations in the region downstream of the liquid length at 10–20 mm axial distance from the nozzle exit, wherein the penetration rate is lower with the coarser mesh. Although the amount of momentum transfer is accurately predicted, the profiles of gaseous phase velocity and mixture fraction distribution have large radial gradient in the near-nozzle region and cannot be sufficiently resolved by the coarse mesh, which leads to flat spray profile (Figs. 5.6a, b and 5.7a, b) and slow penetration rate. However, as the spray keeps penetrating into farther downstream region, the growth rates of penetration for a different mesh resolution become similar, and the transient penetration profiles are all in good agreement with the experimental data for 1.5–3 ms after the start of injection (ASI). Similarly, in the region of 3–5 cm axial distance, grid convergence is achieved for the prediction of mass fraction distribution, indicating a good grid independency of the current spray model. The 2D mesh with 0.5 cm resolution gives the best match with the experimental measurement under both non-reacting conditions and is used for the rest of this section exclusively.

Fig. 5.6

Grid sensitivity for 900 K, 22.8 kg/m³ operating condition (Yue et al. 2017). Black lines are the experimental results; gray area indicates uncertainty; red lines are results of the 0.5° sector mesh (2D) with a resolution of 0.7 mm; green and blue lines are results of cubic meshes with a resolution of 1 and 1.5 mm, respectively. a Vapor and liquid penetrations; mixture fractions b along spray centerline, and c–f along radial directions at four axial distances from the nozzle exit at quasi-steady state

Fig. 5.7

Grid sensitivity for 1100 K, 15.2 kg/m³ operating condition. See Fig. 5.6 for more explanation

4.3 Effects of Turbulence Model

As mentioned in Sect. 5.3.5, a generalized RNG model is used for the turbulence modeling in this work. However, for comparison, simulations were also performed using the modified RNG model (Han et al. 1995) and the standard k-ε model (Launder et al. 1972), and the results are plotted as green lines and blue lines, respectively, in Figs. 5.8 and 5.9. It is seen that the standard k-ε model overpredicts the spray dispersion with slower penetration, which is considered to be a result of an unchanged model constant used for both compressing and expanding flows $\left( {C_{3} = - 1.0} \right)$. For 22.8 kg/m³, the mRNG model gives a similar result as the gRNG model and only slightly overpredicts the dispersion at downstream locations. This is largely because the compressibility of flow is also considered in mRNG model $\left( {C_{3} = \left\{ {\begin{array}{*{20}c} {1.726,{\mkern 1mu} {\mkern 1mu} {\text{if}}{\mkern 1mu} \nabla \cdot {\mathbf{u}} < 0} \\ { - 0.90,{\mkern 1mu} {\mkern 1mu} {\text{if}}{\mkern 1mu} \nabla \cdot {\mathbf{u}} > 0} \\ \end{array} } \right.} \right)$). However, the discrepancy grows for a lower ambient density condition, where mRNG predicts more similarly to the standard k-ε model, as can be seen in Fig. 5.9, indicating that there is better flexibility of the gRNG model in spray modeling for a wide range of operating conditions which is obtained by modeling $C_{3}$ as a function of strain rate; see Table 5.2.

Fig. 5.8

Influence of turbulence models for 900 K, 22.8 kg/m³ operating condition. Black lines are the experimental results; gray area indicates uncertainty; red, green, and blue lines are CFD results of gRNG, mRNG, and standard k-ε models

Fig. 5.9

Influence of turbulence models for 1100 K, 15.2 kg/m³ operating condition. See Fig. 5.8 for more explanation

4.4 Comparison of the EP and Classical Spray Models

It is also of great interest to compare the EP model with a classical Lagrangian spray modeling approach, which includes the hybrid KH-RT breakup model (Beale et al. 1999), the radius-of-influence (ROI) drop collision model (Munnannur et al. 2009), the gas-jet model (Abani et al. 2007), and the discrete multi-component (DMC) vaporization model (Ra et al. 2009). This integrated approach has been widely employed in simulations of fuel injection in IC engines. In this work, the spray model constants were optimized for condition of 900 K, 22.8 kg/m³ (Wang et al. 2014) and were kept unchanged for all the other cases here.

Figures 5.10 and 5.11 compare the predicted spray penetration and fuel vapor distribution by the EP (red lines) and the classical spray model (green lines), for 900 K, 22.8 kg/m³ and 1100 K, 15.2 kg/m³ operating conditions, respectively. Meanwhile, the KH-RT breakup and ROI collision models were also enabled in couple with the EP model, as shown by the blue lines, to assess the importance of these non-equilibrium processes. The three modeling approaches are seen to give very similar predictions that are also in good agreement with the experimental data. The consideration of drop breakup and collision is shown to have a small influence on the EP model prediction, since these processes neither affect the air entrainment and mixing nor do they have an influence on the Lagrangian-to-Eulerian liquid conversion. The only effect that breakup and collision could have on the EP model prediction is through the calculation of drop drag force, which depends on drop size. However, as seen in Figs. 5.10 and 5.11, this influence is seen to be negligible for such a vaporizing condition with high injection pressure. By contrast, the breakup and collision models are critical in the classical approach since they determine the droplet surface area density and the evaporation rate, which usually have a number of model constants that can be optimized to achieve good prediction for spray simulations. A comparison of liquid lengths predicted by the EP model and the classical model under various ambient temperatures and ambient densities is given in Fig. 5.12. The EP model consistently provides accurate prediction under all conditions, while the classical spray model is shown to be less dependent on the ambient temperature wherein a case-by-case adjustment in the model constants might be necessary to match the experiment under a wide range of conditions. Another advantage of the EP spray model is better computational efficiency since the non-equilibrium processes of breakup, collision, and vaporization are bypassed, as illustrated in Table 5.5. It is also worth to note that the DMC vaporization model used in the classical spray model applies Raoult’s law and the Clausius–Clapeyron equation to determine the equilibrium at liquid–gas interfaces, which are less accurate at elevated pressures, e.g., engine operating conditions.

Fig. 5.10

Comparisons of the EP and classical spray models for 900 K, 22.8 kg/m³ operating condition (Yue et al. 2017). Black lines are the experimental results; gray area indicates uncertainty; red lines are EP model without breakup and collision models; green lines are classical spray model, which features droplet breakup, collision, vaporization models; blue lines are EP model with breakup and collision models

Fig. 5.11

Comparisons of the EP and classical spray models for 1100 K, 15.2 kg/m³ operating condition. See Fig. 5.10 for more explanation

Fig. 5.12

Quasi-steady-state liquid length for various ambient temperatures and densities (Yue et al. 2017). Red: 22.8 kg/m³; blue: 15.2 kg/m³; and black: 7.6 kg/m³. Solid symbols: experimental results; half symbol: EP spray model; and open symbol: classical spray model

Table 5.5 Computational time for the EP and classical spray model

4.5 Flame Lift-off Length and Soot Formation

The flame lift-off length and spatial distribution of soot emissions are used to validate reacting sprays of cases 3–7 in Table 5.3. The comparison of CFD predictions and experimental measurement for quasi-steady-state sprays is presented in Fig. 5.13. The spatial distributions of soot volume fraction are shown by the color contour, and the same scales are applied for both CFD and experimental results. The blue dashed lines mark the locations of flame lift-off lengths. The constants for soot model were kept unchanged for all the operating conditions. At lower ambient temperatures and lower O₂ content, the ignition occurs further downstream with increased lift-off length, which results in better fuel/air mixing and less soot formation. The prediction of soot volume fraction is in good agreement with the experimental data. The location and area of the soot cloud are also well captured, which is attributed to the accurate prediction of mixture fraction in the downstream area.

Fig. 5.13

Comparisons of soot from the EP model CFD predictions (Yue et al. 2017) and experimental measurements (Skeen et al. 2016). a–e give comparisons of the experiment (left) and CFD (right) for different operating conditions. Color contours indicate the soot volume fraction; blue dashed lines indicate lift-off length

5 Gasoline Direct Injection (GDI) Simulation

The previous sections present validation and applications of the EP spray model in simulations of high-pressure, diesel-like fuel sprays. The success of those simulations verifies the mixing-controlled characteristics of high-pressure diesel sprays. On the other hand, GDI engines have drawn increasing attention due to a number of advantages over port fuel injection (PFI) systems, such as accurate fuel delivery, less cycle-to-cycle variation (CCV), better fuel economy with extended knock-limited operating condition, and potential for stratified lean operation (Zhao et al. 1999). Fuel injection is one of the critical processes in a GDI engine, especially for spray-guided combustion systems, which make use of the injection process to form a stably ignitable fuel/air mixture around the spark plug. The multi-hole GDI nozzle has the advantage of providing a stable spray structure, and it is less sensitive to the operating conditions compared to pressure-swirl atomizers (Mitroglou et al. 2007). Despite the similarity to multi-hole diesel injectors, multi-hole gasoline injectors usually feature a narrower drill angle, smaller length/diameter (L/D) ratios, a step-hole design, and a relatively lower fuel pressure (10–40 MPa), with a more volatile, less viscous fuel being injected into a cooler and lower density chamber. In this section, the EP model is applied to simulate sprays of a multi-hole GDI injector and its controlling mechanism is also examined.

The experimental data were taken in a constant volume spray chamber by Parrish (2014), Parrish and Zink (2012). The operating conditions can be found in Table 5.6, showing that three ambient densities were targeted, with temperatures varying from 400 to 900 K. The injector has eight holes with a stepped-hole geometry and a nominal-included angle of 60°. However, the measured value of 50° was used in the simulations. Iso-octane was used as a surrogate for gasoline in the experiments, and the injection pressure was held at 20 MPa for all tested conditions. The duration of the injection was 766 μs, which is shorter and more transient than the ECN Spray A cases. Schlieren and Mie-scatter imagining were used to track the envelopes of the vapor jets and liquid sprays, respectively. Unlike for a single-hole injector, the liquid and vapor penetrations were evaluated for the entire spray rather than for a single plume, and the distance from the nozzle exit to the jet tip was measured along the direction of the injector axis.

Table 5.6 Operating conditions and injector specification for GM GDI (Parrish 2014)

For the simulation setup, the computational domain was a cylinder with a diameter of 10 cm and a height of 10 cm. A 45° sector mesh was used, as shown in Fig. 5.14, to simulate one spray plume with the injector located at the top center. A clip plane colored by the mixture fraction is also shown in Fig. 5.14 to illustrate the injector location and spray plume direction. In this case, plume-to-plume interaction is simplified by assuming each plume is identical. The mesh resolution is 0.5 mm * 0.5 mm * 4.5° near the nozzle and transitions to 2.75 mm * 2.75 mm * 4.5° at the sides. As mentioned in Sect. 5.3.1, the model constant $C_{\theta }$ in the spreading angle correlation depends on the injector configuration and nozzle flow, e.g., cavitation. Therefore, the value of $C_{\theta }$ for a GDI injector is expected to be different than the value used for the Spray A injectors. Due to the lack of the experimental measurement of spreading angles, $C_{\theta }$ was determined to be 0.6, based on a best match of jet penetrations for the 6 kg/m³ ambient density cases.

Fig. 5.14

Computational domain for one spray plume simulation

The predictions of liquid and vapor envelopes are compared with the experimental measurements for several conditions, as shown in Figs. 5.15, 5.16, and 5.17, for three ambient temperatures, respectively. Three ambient densities are shown for each ambient temperature. For each operating condition, results are compared at 0.5, 1.0, and 1.5 ms after the start of injection in each row. The experimental results are shown on the left in each pair of the experiment/CFD comparison. Red lines and green lines outline the liquid and vapor envelopes, respectively, and the black dashed lines mark the measured spray-included angle. For the CFD predictions, white clouds represent the vapor plume and red clouds represent the liquid jet. The result of a simulated single plume in a sector mesh was replicated and rotated to form an eight-plume spray in order to compare with the experimental results.

Fig. 5.15

Liquid and vapor envelopes for 500 K conditions. Ambient densities are 3, 6, 9 kg/m³ from left to right. Each row corresponds to 0.5, 1.0, 1.5 ms after start of injection, respectively. For the experiment, red and green lines outline the envelopes of liquid and vapor phases, respectively. For CFD, red and white clouds represent liquid jet and vapor plume, respectively

Fig. 5.16

Liquid and vapor envelopes for 700 K conditions. See Fig. 5.15 for more explanations

Fig. 5.17

Liquid and vapor envelopes for 900 K conditions. See Fig. 5.15 for more explanations

The general trend is that both spray penetration and liquid residence time decrease with increasing ambient temperature and increasing ambient density, which is observed in both the experimental results and the CFD predictions. According to the mixing-controlled spray analysis, higher ambient temperature at constant ambient density results in higher internal energy per unit entrained gas and consequently leads to faster vaporization and shorter liquid length. On the other hand, higher ambient density at constant ambient temperature results in a wider spray cone angle that leads to a faster entrainment rate; thus, the vaporization is also accelerated. The included angle and shape of the vapor envelopes seen in the experiments are accurately captured by the simulations at each transient time for each operating condition. The fingerlike shape of the liquid jet is also well predicted by the model, with slight overprediction in liquid residence time after the end of injection for low ambient density conditions, as can be seen at 1.5 ms ASI of the 500 K, 3 kg/m³ condition and at 1.0 ms ASI of the 900 K, 3 kg/m³ condition.

The liquid and vapor penetrations are plotted as line graphs in Fig. 5.18. Solid lines are the experimental results, while dashed lines are the CFD predictions and colors indicate different ambient densities. Similar to observations in the 2D spray envelopes, the transient penetration of the vapor plume is accurately predicted by the model predictions with less than 5% error even at 3.5 ms ASI. Quasi-steady state of liquid length is reached after an initial transient period for both the 700 and 900 K cases. However, such a quasi-steady period is not seen for 500 K, indicating the quasi-steady-state liquid length cannot be reached within such a short duration of injection. Even though the current EP spray model is derived based on the experiments of long-duration, quasi-steady-state fuel injection, its application in the present GDI simulations is seen to capture the transient behavior of a short-duration injection very well, as shown in the predictions of liquid penetration for the 6 and 9 kg/m³ conditions. Furthermore, although the liquid length is considerably overpredicted at low ambient density conditions, the transient vapor penetration is still accurately captured by the model.

Fig. 5.18

Liquid and vapor penetrations. a, b, and c are liquid penetrations for 500, 700, and 900 K ambient temperatures, respectively; d, e, and f are their corresponding vapor penetrations. Black, red, and blue lines correspond to 3, 6, and 9 kg/m³ ambient densities, respectively. Solid lines are the experimental measurement, and dashed lines are CFD predictions

Figure 5.19 shows the maximum liquid length as a function of ambient temperature for each ambient density condition. Excellent agreements can be found between the experimental results and the CFD predictions for most cases. However, the error in the prediction of maximum liquid length grows with decreasing ambient density and temperature. In this case, the validity of mixing-controlled assumption is considered not to be the reason of such error, as the phase equilibrium, mixing-controlled vaporization process would be expected to always give a faster vaporization and a shorter liquid length compared to the non-equilibrium vaporization process. Possibly, the constant value of $C_{L}$ in Eq. (5.6) is questionable. $C_{L}$ has a theoretical value of 0.38 from the derivation of Siebers’ scaling law and was adjusted to 0.62 in order to match the n-hexadecane and heptamethylnonane liquid length data (Siebers 1999). The change in $C_{L}$ is considered to be a compensation for errors introduced by assumptions made when deriving the liquid length scaling law, which should not be expected to be the same when the operating condition changes significantly.

Fig. 5.19

Liquid length as a function of ambient temperature. Black, red, blue lines correspond to 3, 6, 9 kg/m³ ambient densities, respectively. Solid triangles are the experimental results; hollow triangles are CFD predictions

Moreover, the accuracy of the correlation for the spray spreading angle $\theta$ can also affect the liquid length prediction. Particularly, liquid cavitation within the nozzle passages is a possible agency in the determination of $C_{\theta }$ in Eq. (5.15) (Reitz et al. 1982), which is not considered in this study. The cavitation number K is usually used to quantify the cavitation transition, which is defined as $K = \left( {P_{\text{inj}} - P_{\text{amb}} } \right)/\left( {P_{\text{amb}} - P_{v} } \right)$. $P_{\text{inj}}$ is the injection pressure, $P_{\text{amb}}$ is the ambient pressure, and $P_{v}$ is the fuel vapor pressure. For the studied cases in this section, the value of K ranges from 7.5 for the highest ambient pressure condition to 70.4 for the lowest ambient pressure condition, which is estimated using $P_{v}$ of 0.78 for iso-octane at 363 K. A higher K value indicates higher tendency of cavitation and consequently wider spreading angle. Thus, the consideration of the K factor could mitigate the deviation in liquid length prediction seen at low-pressure conditions. Nonetheless, the current form of the EP spray model provides satisfying results for most engine-relevant conditions, especially for the vapor plume, which is essential in engine combustion simulations.

6 Summary

Experimental studies have shown that the vaporization process of a high injection pressure engine spray is controlled by the hot ambient gas entrainment and the overall fuel/air mixing within the spray, instead of being controlled by transport rates of mass and energy at spray droplet surfaces. This conclusion is valid for fuel injection problem under most of IC engine operating conditions. However, most CFD models that have been applied in IC engine simulations use the LDEF method for the modeling of the two-phase flow process of liquid fuel injection, where the non-equilibrium processes of drop breakup, collision and coalescence, and liquid/vapor interfacial vaporization are modeled by tracking droplets with considerable modeling and computational effort. An equilibrium phase (EP) spray model has been recently developed and implemented into an open-source CFD program, KIVA-3vr2 (Amsden 1999), for application to IC engine simulation, where the role of mixing-controlled vaporization is emphasized by the introduction of an Eulerian liquid phase into the LDEF framework and employing an advanced phase equilibrium solver. The EP spray model was developed based on a jet theory and a phase equilibrium assumption, without the need for modeling drop breakup, collision, and surface vaporization processes.

The integrated model was validated widely in the ECN Spray A, as well as GDI sprays. The validations confirm the good accuracy and grid independency of the EP model in predictions of liquid/vapor penetrations, fuel mass fraction distributions for the non-reacting sprays, and heat release rates, pressure traces, and emission formation for reacting cases, over a wide range of operating conditions (700 K to 1400 K, 7.6–22.8 kg/m³ for diesel sprays; 500–900 K, 3–9 kg/m³ for GDI sprays) without the need for tuning of model constants, except for the constant in the spreading angle correlation, which is expected to change for different injector configurations. The accuracy of the liquid length prediction for GDI sprays at low ambient densities could potentially be improved even further by using a comprehensive spray cone angle model that considers in-nozzle flow, cavitation, etc. Moreover, the EP model was also proven to be 37% more computationally efficient than the widely used ‘classical’ model for the studied cases.