Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

According to a definition by Collier and Thome (2001), boiling is ‘the process of addition of heat to a liquid in such a way that generation of vapor occurs.’ Boiling heat transfer is a very efficient heat transport mechanism and is employed in a wide field of applications. Heat removal by a boiling fluid is encountered in a variety of engineering systems ranging from large nuclear/conventional power plants to cooling of tiny high-performance electronic chips, for the reason it can transfer large heat fluxes across relatively small temperature differences. Due to its intensive use in engineering applications and newer areas of application (e.g, microheatpipes, biochips), research in boiling has intensified over time in the last hundred years (Collier and Thome 2001; Kakaç et al. 1988; Bergles 1988). The energy crunch and its associated environmental consequences have made it a crying need for all appliances to strive for higher thermal efficiency which in turn have led to further efforts to enhance boiling heat transfer.

A comprehensive review of research up to the 1970s has been provided by Bergles (1981a) supplemented by the review by Nishikawa (1987). More recent review articles by Dhir (1998) and Mangalik (2006) summarize the current achievements in the field of boiling heat transfer research.

2 Boiling Phenomena

In this section, the phenomenon of boiling and major achievements in boiling research is briefly described. Heat transfer mechanisms during boiling are still not well understood and are an area of research. One of the first comprehensive studies in this area was the pioneering work of Jakob and Fritz (1931); it was followed by Nukiyama (1934) who established the boiling curve for nucleate boiling conditions, i.e., when the generation of vapor is induced via heating of a solid surface. This work has become a kind of benchmark for nucleate boiling investigations. Subsequently, McAdams et al. (1949) extended the nucleate boiling curve to conditions whereby boiling at a surface is induced in a pool of liquid at a temperature below saturation (‘subcooled’ boiling). With the rapid development in the field of nuclear power and related safety issues, there was explosive growth in the number of publications in the area of nucleate boiling heat transfer. In particular, much attention was devoted to understanding fault conditions leading to uncontrollable boiling modes that can cause damage of the nuclear fuel rods because of critical heat flux (CHF) and predict accurately the heat transfer via circulation of fluids undergoing subcooled boiling (Nishikawa 1987; Bergles 1981b).

In this context, boiling in a stationary pool of liquid at a horizontal surface (pool boiling) and boiling in ducts with a strong imposed liquid flow (flow boiling) are the most studied phenomena. A typical pool boiling curve is shown in Fig. 15.1.

Fig. 15.1
figure 1

Pool boiling curve

Full size image

In pool boiling, different regimes of heat transfer are (Collier and Thome 2001; van Stralen and Cole 1979):

  1. (i)

    Partial nucleate boiling: where individual bubbles form and detach from the heated surface without any interaction. High heat transfer rates are characteristic of this region.

  2. (ii)

    Nucleate boiling: With the increase of heat flux, numerous bubble nucleation sites are activated and steady columns of vapor bubbles are generated. However, as more and more area of the heating element is blanketed by vapor the required wall superheat increases due to the insulating effect of the vapor and the overall heat removal rate decreases dramatically (a typical instance of CHF).

  3. (iii)

    Transition to film boiling: When CHF is reached, a large part of the surface of the heater is covered with vapor. With a slight increase in heat flux, the wall temperature increases inordinately, damaging the heating element.

  4. (iv)

    Stable film boiling: A stable vapor layer is formed in this regime, and the liquid phase is separated from the heated wall.

Numerous experimental studies have been carried out to study the various aspects of boiling: Bubble dynamics, nucleation site density, the formation and evaporation of thin liquid layers beneath growing bubbles are among the most studied topics (Ramaswamy et al. 2002; Cole 1967; Ivey 1967; McHale and Garimella 2010).

In isolated bubbles boiling (i.e., when there is some space between nucleation sites and bubbles do not interact, for example, do not merge or disturb the flow pattern near each other), it is sufficient to focus on any single bubble on the surface and observe local parameters (Duan et al. 2013; Jung and Kim 2014). Figure 15.2 shows the schematic of a single bubble being formed during nucleate boiling. For typical fluids, in low-pressure pool boiling conditions the liquid near the horizontal surface is highly superheated, which causes rapid bubble expansion (Rayleigh 1917; Plesset and Zwick 1954, 1955; Scriven 1958; Prosperetti and Plesset 1978; Prosperetti 2017). These almost hemispherical bubbles leave behind on the solid surface a liquid layer (microlayer) which then evaporates and contributes itself to bubble expansion (Koffman and Plesset 1983; Jung and Kim 2018). For high-pressure pool boiling, the reduced density ratio (Scriven 1958) reduces the expansion rate and no microlayer is formed (Jung and Kim 2018). In high-pressure boiling, bubble departure diameters are much smaller than in low-pressure conditions. It has been speculated that this could be due to a decrease in wettability of typical metallic surfaces as the temperature increases (Ardron et al. 2017). Figure 15.3 shows images of a boiling bubble taken with the help of a high-speed camera.

Fig. 15.2
figure 2

Schematic of single bubble nucleate boiling

Full size image
Fig. 15.3
figure 3

Adapted from Jung and Kim (2014)

High-speed camera images of a boiling bubble and corresponding liquid–vapor phase boundary, temperature, and heat flux distributions at the boiling surface.

Full size image

In flow boiling conditions, the basic mechanism of heat transfer remains the same. However, due to forced convection the liquid is only slightly superheated near the wall and bubble behavior is dictated mainly by hydrodynamic aspects: lift, drag, buoyancy, surface tension, and wall adhesion forces (Klausner et al. 1993; Thorncroft et al. 1998). Figure 15.4 illustrates a typical flow boiling regime in a vertical tube.

Fig. 15.4
figure 4

Adapted from Collier and Thome (2001)

Flow boiling regime in a vertical tube.

Full size image

One aspect of boiling phenomena that has always worried designers is CHF. As discussed earlier, when the heat flux is increased, conditions could be reached whereby increasing the power input causes the surface to be entirely covered by a vapor blanket, due to, for example, bubble interactions and ‘crowding.’ This causes the temperature to increase inordinately following a slight perturbation in the flow parameters (Hewitt 1998a, b). It has become imperative to study the collective behavior of bubbles, which is much more difficult than modeling the behavior of a single bubble. This collective behavior is poorly understood, and the current understanding is empirical or phenomenological in nature. There are different mechanisms for CHF prevalent in published literature, starting with Kutateladzes (1961) pioneering work to the popular work by Zuber (1958). An extensive and very recent two-part review by Liang and Mudawar (2018a, b) is an excellent read on the subject.

Over time measurement techniques have developed and very small length and time scales are now being resolved, which has made the measurement of instantaneous heat transfer beneath a bubble possible with remarkable accuracy. High-speed infrared thermography (Schweizer and Stephan 2009; Wagner et al. 2006) provides a very detailed insight about the transient heat transfer between the heating element and the fluid. Another very important area of boiling research is boiling on microstructured surfaces, as nucleate boiling heat transfer and CHF enhancement are possible via employing carefully engineered surfaces. Several review articles on the enhancement of boiling heat transfer on microstructured surfaces have been reported (Shojaeian and Kosar 2015; Kim 2011; Ahn and Kim 2012; Dong et al. 2015).

As stated earlier, boiling is a complex physical process due to the interaction of a great variety of important parameters. A complete theoretical model which could predict boiling heat fluxes only as function of a given set of input parameters is yet to be developed. Concurrent with experimental studies and empirical correlations, efforts are aimed at understanding the physical mechanisms of boiling in depth. A consensus is still lacking among researchers in this field regarding the dominant mechanism of heat transfer during boiling. Over time different theoretical models have been proposed for boiling heat transfer. One of the first papers that discussed different mechanisms of boiling heat transfer was by Han and Griffith (1965a, b). They described two methods of heat transfer: bulk convection, in which the superheated liquid is removed away from the wall as the bubble detaches and natural convection from the heated wall to the fluid in the space between bubble nucleation locations. Cooper and Lyod (1969) inferred the existence of a thin liquid film beneath boiling bubbles, called a microlayer, which enables the high heat transfer during bubble growth. Kern and Stephan (2003, 2004) developed a theory where they described the mechanisms of the transport of heat from the wall to the fluid. Due to the separation of scales, the model considers the transport phenomena on microscopic and macroscopic scales. A substantial part of the heat from the wall flows through the microlayer where the thermal resistances of the liquid film is negligible which leads to high heat transfer and hence governs the overall heat transfer performance. At a macroscopic scale, the liquid in the vicinity of a rising bubble is set in motion, which results in an enhanced heat transfer and transient heat conduction due to rewetting of the heater surface.

Mechanistic wall heat transfer models proposed by De Valle and Kenning (1985) or Kurul and Podowski (1990) use very crude theory of heat flux partitioning along the lines of the Han and Griffith model, enabling little physical understanding. These models break down when bubbles begin to interact with each other (Basu 2003).

3 Numerical Modeling

Boiling flows belong to a subset of a much larger group of flows classified as multiphase flows. Efforts to simulate multiphase flows have been one of the major challenge areas since the inception of computational fluid dynamics (CFD). The main difficulty is solving the Navier–Stokes equations with a deforming phase boundary. In the last two decades, thanks to exponential rise of computing power and development of new numerical tools (Prosperrotti and Trygvassion 2007; Yeoh and Tu 2010), major progress has been achieved in this field such that numerical simulation of boiling is also established as a tool that can complement experimental investigations in order to understand the physics of boiling better. The crux of simulation of multiphase flows is the accurate identification of the interface dynamics through which flow regimes can be defined and momentum and energy transfer mechanisms between the phases can be quantified.

There are mainly two major approaches of numerical simulation of boiling flows: (a) two-fluid models or interpenetrating media approach (Ishii and Hibiki 2011) and (b) single-fluid formulation or interface tracking methods (ITMs) (Tryggvasson et al. 2001). In interpenetrating media approach, each point in the mixture is occupied simultaneously by both phases, and separate conservation equations are required for each field. In single-fluid formalism, the topology and dynamics of the interface are directly simulated by the use of direct interface tracking methods. In the last decade, newer techniques like lattice Boltzmann method and phase field method have been used for the simulation of boiling flows. In the subsequent sections, we will discuss each of these major approaches in detail.

3.1 Interpenetrating Media

The main challenge in simulating boiling flows is posed by the requirement of capturing the energy transfer from wall to fluid associate to the formation and release of bubbles at the heat transfer surface. Interpenetrating continua methods predict the evolution of spatially and temporally averaged quantities and provide no means of mechanistic modeling the behavior of bubbles near the wall. Typically, in such circumstances one computational near-wall cell is several times the bubble characteristic dimension.

Various wall boiling models are used in commercial CFD codes (Colombo and Fairweather 2016) with the aim of predicting energy transfer from wall to fluid. All of these approaches rely on heat flux partitioning, and various correlations for wall heat flux partitioning have been proposed in the literature. Mechanistic models based on relevant heat transfer mechanisms occurring during the boiling process are used for the estimation of the wall heat flux as well as the partitioning of the wall heat flux between the liquid and vapor phases. Most numerical simulations of boiling flow are mainly based on the use of these mechanistic models, of which a large majority are extensions of the model proposed by Kurul and Podowski of the Rensselaer Polytechnic Institute (RPI) (Kurul and Podowski 1990). Following Griffith (Han and Griffith 1965a), the wall heat flux is usually partitioned into three heat flux components: convective heat flux, evaporative heat flux, and ‘quenching’ (i.e., transient conduction to the liquid) heat flux. These models rely on previous knowledge of three unknown parameters, which should be modeled accurately: nucleation density (Na), bubble departure diameter (Db), and bubble departure frequency (f).

The Eulerian–Eulerian two-fluid model represents the most detailed macroscopic formulation of the thermal and hydrodynamic characteristics of any two-phase systems. As noted, the problem with this method is the specification of closure relations for mass, momentum, and energy exchanges across the interface and calculating the corresponding interfacial area. Here, the field equations are expressed by six conservation equations of mass, momentum, and energy. For boiling flow, three equations are used to model the bubbles (i.e., the vapor phase) while the three equations are used to model the liquid phase. The interfacial terms arising out of the averaging of the equations represent the mass, momentum, and energy transfers through the interface between the phases. The existence of these interfacial transfer terms is rather significant as they determine the rate of phase changes, and the degree of thermal non-equilibrium between phases. Most importantly, they provide the necessary closure relations required in two the fluid model.

In the mass conservation equations, mass transfer is accounted between phases due to the evaporation from liquid to bubbles or bubbles being condensing in the bulk liquid (which is at a temperature below saturation). In the momentum conservation equations, the important interfacial effects between the liquid and gas phases due to the drag force as well as other possible so-called non-drag forces in the form of lift, wall lubrication, and turbulent dispersion are incorporated. In the energy conservation equations, the interfacial heat transfer accounts for the phase change due to evaporation/condensation. Also, the prediction of the local bubble sizes in the subcooled liquid flow is strongly influenced by factors like turbulent dispersion, local coolant temperature fluctuations occurring near the heated wall.

The two set of conservation equations governing mass, momentum, and energy can be written as:

Liquid-phase continuity equation

$$ \frac{{\partial \rho_{l} \alpha_{l} }}{\partial t} + \nabla \,.\,\left( {\rho_{l} \alpha_{l} \overline{{u_{l} }} } \right) =\Gamma _{lg} $$

Vapor-phase continuity equation

$$ \frac{{\partial \rho_{g} \alpha_{g} }}{\partial t} + \nabla \,.\,\left( {\rho_{g} \alpha_{g} \overline{{u_{g} }} } \right) =\Gamma _{lg} $$

Liquid-phase momentum equation

$$ \begin{aligned} & \frac{{\partial \rho_{l} \alpha_{l} \overline{u} }}{\partial t} + \nabla \,.\,\left( {\rho_{l} \alpha_{l} \overline{{u }}_{l} \overline{{u}}_{l}} \right) = - \alpha_{l} \nabla P + \alpha_{l} \rho_{l} \overrightarrow {g} \\ & \quad \nabla \,.\,\left[ {\alpha_{l} \mu_{l}^{\text{eff}} \left( {\nabla \overline{{u}}_{l} + \left( {\nabla \overline{{u}}_{l} } \right)^{T} } \right)} \right] + \left( {\Gamma_{lg} \overline{{u}}_{g} - \Gamma_{gl} \overline{{u}}_{l} } \right) + F_{lg} \\ \end{aligned} $$

Vapor-phase momentum equation

$$ \begin{aligned} & \frac{{\partial \rho_{g} \alpha_{g} \overline{u}_{g} }}{\partial t} + \nabla \,.\,\left( {\rho_{g} \alpha_{g} \overline{u}_{g} \overline{u}_{g} } \right) = - \alpha_{g} \nabla P + \alpha_{g} \rho_{g} \overrightarrow {g} \\ & \quad + \nabla \,.\,\left[ {\alpha_{g} \mu_{g}^{\text{eff}} \left( {\nabla \overline{u}_{g} + \left( {\nabla \overline{u}_{g} } \right)^{\text{T}} } \right)} \right] + \left( {\Gamma_{gl} \overline{u}_{l} - \Gamma_{gl} \overline{{u}}_{g} } \right) + F_{gl} \\ \end{aligned} $$

Liquid-phase energy equation

$$ \begin{aligned} \frac{{\partial \rho_{l} \alpha_{l} H_{l} }}{\partial t} + \nabla \,.\,\left( {\rho_{l} \alpha_{l} \overline{{u}}_{l} H_{l} } \right) & = \nabla \,.\,\left[ {\alpha_{l} \lambda_{l} \nabla T_{l} + \frac{{\mu_{Tl} }}{{\Pr_{Tl} }}\nabla H_{l} } \right] \\ & \quad \quad \quad + \left( {\Gamma_{lg} H_{g} - \Gamma_{gl} H_{l} } \right) \\ \end{aligned} $$

Vapor-phase energy equation

$$ \begin{aligned} \frac{{\partial \rho_{g} \alpha_{g} H_{g} }}{\partial t} + \nabla \,.\,\left( {\rho_{g} \alpha_{g} \overline{{u}}_{g} H_{g} } \right) & = \nabla \,.\,\left[ {\alpha_{g} \lambda_{g} \nabla T_{g} + \frac{{\mu_{{T_{g} }} }}{{\Pr_{{T_{g} }} }}\nabla H_{g} } \right] \\ & \quad \quad \quad + \left( {\Gamma_{gl} H_{l} - \Gamma_{lg} H_{g} } \right) \\ \end{aligned} $$

The source term Γlg represents the mass transfer rate due to evaporation or condensation in the bulk subcooled liquid and Γgl = − Γlg. The wall vapor generation rate is modeled in a mechanistic way. Interfacial transfer terms in momentum and energy equations denote transfer from one phase to another. The total interfacial force is the sum of the drag force (Ishii and Zuber 1979), lift force (Drew and Lahey 1979), wall lubrication force (Anglart and Nylund 1996), and turbulence-assisted bubble dispersion force (Antal et al. 1991).

Over time, many researchers (Koncar et al. 2004; Lo 2005) have proposed different techniques for modeling the different interfacial terms; other efforts were directed for the improvement in bubble size modeling and interfacial area concentration modeling. Ishii and Hibiki (2011) were the first to propose a detailed modeling of the interfacial area transport equation. Later, Yeoh and Tu (2005) applied an interfacial area transport equation and bubble number density transport equations in CFD codes for prediction of subcooled boiling flows. Figure 15.5 shows a contour plot of the simulated vapor fraction at the outlet of a pipe during subcooled boiling (Bartolomei and Chanturiya 1967).

Fig. 15.5
figure 5

Prediction of subcooled flow boiling (Bartolomei and Chanturiya 1967) using STAR-CCM+(v9.06)

Full size image

Though different models in two-fluid approach have confirmed the ability of numerical simulations in providing detailed predictions for some cases, significant improvements in model accuracy is required for general applicability. Even when codes are built using a mechanistic approach, numerous empirical closure relations are still required for wall boiling, population balance, and turbulence models. The problem of formulating an all-encompassing closure law arises from the fact that each closure law depends on the specific physical phenomenon.

3.2 Single-Fluid Formalism

In single-fluid formalism, the idea is to simulate the whole field as a single fluid, with variable properties changing sharply at the interphase boundary, which is modeled as having zero thickness.

From a hydrodynamic point of view, the main difficulty is caused by the need of accounting for surface terms (e.g., the surface tension force) in the fundamental transport equations, which are derived for stationary fluid control volumes.

From a thermal point of view, capturing the thermodynamic state of the interface in the presence of phase-change processes represents the main difficulty. Interface thermodynamics cannot be modeled from first principles within the framework of continuum mechanics: The continuum description itself is underpinned by underlying thermodynamic hypotheses (e.g., local equilibrium). Hence, it is necessary to make assumptions about the thermodynamic state of the interface. Most single-fluid methods assume that the interface temperature is equal to the equilibrium saturation temperature corresponding to the system pressure.

Interfacial terms (representing surface forces or energies) are modeled as source terms in the momentum equations. They are written as delta functions at the interface. The unsteady Navier–Stokes equations are solved on a fixed where the position of the interface, or front, is not known a priori and is a part of the solution. Forces such as surface tension are modeled as volumetric source term. The advection equation is solved in a coupled manner to model the motion of the front. With these methods, there are difficulties in computing the curvature, estimation of the surface tension term, modeling wall adhesion, computing evaporative mass transfer at the interface (Fig. 15.6).

Fig. 15.6
figure 6

Schematic of two phases of the same fluid separated by an interface marked by particles

Full size image

The governing equations in single-fluid formalism are

$$ \frac{{\partial u_{j} }}{{\partial x_{j} }} = \nabla \,.\,\overrightarrow {V} = 0 $$
$$ \frac{{\partial \rho_{m} u_{i} }}{\partial t} + \frac{{\partial \rho_{m} u_{j} u_{i} }}{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\mu_{m} \frac{{\partial u_{i} }}{{\partial x_{j} }}} \right] - \frac{\partial p}{{\partial x_{i} }} + \rho_{m} g_{i} + F_{st,i} \delta + \frac{\partial }{{\partial x_{j} }}\left[ {\mu_{m} \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right] $$

The first equation represents volume conservation, whereas the second equation represents momentum equation in conservative form. \( F_{st,i} \delta \) is the surface tension force that acts at the interface. The interface location is tracked by solving an equation for the conserved scalar Φ,

$$ \frac{\partial \Phi }{\partial t} + \frac{{\partial \Phi u_{j} }}{{\partial x_{j} }} = 0. $$

Typically, there are mainly three ITMs which are used for the simulation of boiling heat transfer:

  • The marker-and-cell (MAC) method (Harlow and Welch 1965) in which the interface is marked by massless particles that are convected by the velocity field and are used to reconstruct the interface position.

  • The volume-of-fluid (VOF) method (Hirt and Nichols 1981) in which an advection equation is postulated for predicting the distribution of volume fraction F in space and time. Some geometric properties of the interface are derived from the local F distribution so as to facilitate evaluation of convective fluxes according to the donor–acceptor.

  • The level set (LS) method (Osher and Sethian 1988) which relies in part on the theory of curve and surface evolution (Osher and Fedkiw 2003) and on the link between the front propagation and hyperbolic conservation laws. It is based on the construction of a smooth function, defined everywhere in the computational domain, representing the shortest distance to the front. Negative values correspond to one fluid and positive values to the other. The exact location of the interface corresponds to the zero level of the function.

Besides these three methods, researchers have also developed the arbitrary Lagrangian–Eulerian (ALE) method (Hirt et al. 1974) in which the nodes of the computational mesh may be moved with the continuum in normal Lagrangian fashion or be held fixed in Eulerian manner.

The main difficulty in using the marker-and-cell (MAC) method or the volume-of-fluid (VOF) method is maintaining a sharp boundary between the different fluids and the computation of the surface tension at the interface. Brackbill et al. (1992) proposed the continuum surface force (CSF) model in which the surface force was distributed volumetrically. This to some extent solved the problem of accounting for surface forces in the framework of an Eulerian control volume approach. The problem with the CSF model is its impracticality of computation of the curvature in three spatial dimensions and associated rise of spurious currents; Nandi and Date (2009a, b) formulated a method of calculating curvature from fluid dynamic consideration and were able to reduce the computational effort involved, and it also showed significant reduction of spurious currents.

Tryggvason and co-workers (Tryggvasson et al. 2001; Unverdi and Tryggvason 1992) extended the original MAC method for simulating boiling flows. Esmaeli and Trygvason simulated multimode film boiling on horizontal surfaces and boiling in complex geometries (Esmaeeli and Tryggvason 2004). Their method predicted the interface curvature very accurately which in turn helped improved simulation of very small bubbles. However, microscale heat transfer at the solid–liquid–vapor (‘three-phase’) contact line at the bubble base, or the transient heat conduction in the solid wall, is not accounted for their model. Figure 15.7 shows the evolution of the interface during film boiling.

Fig. 15.7
figure 7

(from Esmaeeli and Tryggvason 2004)

Evolution of a liquid–vapor interface and velocity field during film boiling process

Full size image

Welch and Wilson applied VOF methods to simulate film boiling (Welch and Wilson 2000), implementing a model for phase change suitable for the VOF framework. Subsequently, Welch and Rachidi (2002) extended the model for simulating saturated horizontal film boiling including the conjugate heat transfer with the solid wall. This relaxed the idealization of uniform wall superheat or uniform wall heat flux boundary conditions. Sato and Niceno (2018) used a color function (similar to VOF), to develop a somewhat different numerical approach to simulate nucleate pool boiling, employing an interface-sharpening algorithm. They took into account the conjugate heat transfer between the solid wall and the fluid domains and used their own depletable microlayer model (Sato and Niceno 2015) for computing its vaporization.

Dhir (2001) and co-workers used LS method for various boiling simulations for a wide range of configurations. Son and Dhir (1998) incorporated the effect of phase change into a modified LS method for simulation of film boiling, while Son et al. (1999) developed a microlayer model for estimating single bubble heat transfer associated with nucleate pool boiling. The model accounts for the microscale heat and fluid flow.

VOF methods typically have the problem of generating smeared interfaces, whereas the LS method captures the interface very accurately but leads to violation of mass conservation. A combination of level set–VOF method (CLSVOF) was proposed by Sussman and Puckett (2000), which combined the advantages of both the methods while avoiding the shortcomings. In this method, LS is used only to compute the geometric properties at the interface while the indicator function is advected using the VOF approach. Biswas (Tomar et al. 2005) and Tao (Sun and Tao 2010), among other researchers, used this method for simulation of boiling flows.

Cerne et al. (2001) proposed a coupled Eulerian–Eulerian and VOF model. In the computational domain where the grid resolution is fine enough to allow surface tracking, the VOF method is used and Eulerian two-fluid model is used in regions where the flow is dispersed. Each model uses a separate set of equations suitable for description of the two-phase flow. A ‘switching parameter’ based on the indicator function in the VOF method is used for the transition between the models.

3.3 Other Methods

Classically, at a macroscopic scale, an interface between a liquid and its vapor is modeled as a surface of discontinuity with properties like surface tension. However, at a microscopic scale, an interface has nonzero thickness and all forces at the interface are smoothly distributed. Therefore, the general equations of fluid mechanics can be applied to describe a liquid–vapor system with interfaces.

Diffuse interface models provide a way (Anderson et al. 1998) of modeling all forces at the interface as continuum forces and the discontinuities at the interface are smoothed by varying them continuously over thin interfacial layers. Phase field model is one of such models, which is being applied for the calculation of two-phase flows (Jacqmin 1999; Chen and Doolen 1998). This model allows the simulation of interface movement and topological changes on fixed grids. The Navier–Stokes equations are modified by the addition of the continuum forcing term which is a function of composition variable (C) and its chemical potential. The equation for interface advection is replaced by a continuum advective–diffusion equation, with diffusion driven by C’s chemical potential gradients, and the liquid–vapor interface is described as a three-dimensional continuous medium across which physical properties have strong but continuous variations.

Phase field methods appear to have several potential advantages over the VOF-LS approach. It can capture interface deformations such as coalescence and interface break-up in an energy-dissipative fashion without losing mass. It is easy to implement in three dimensions and unstructured grids and is free of spurious currents. However, the phase field model also has its drawbacks. One has to accurately model relevant the physical phenomena, and the interface layers have to be very thin, and for this, the numerical phase field interfaces are typically kept four to eight cells wide. But this brings its own problems since large gradients now must be resolved computationally.

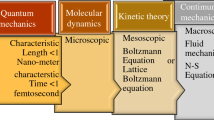
In recent decades, the lattice Boltzmann method (LBM) (Chen and Doolen 1998; Mohamad 2011) has emerged as another method tool for solving the Navier–Stokes equations. LBM is based on microscopic models and mesoscopic kinetic equations. It originated from Ludwig Boltzmann’s kinetic theory of gases. The fundamental idea is that gases/fluids can be imagined as consisting of a large number of small particles moving with Brownian motion. The exchange of momentum and energy is because of elastic collision between the particles. The LBM simplifies Boltzmann’s original idea of gas dynamics by reducing the number of particles and confining them to the nodes of a lattice.

In recent years, the lattice Boltzmann method (LBM) has been applied to simulate multiphase flow, in which the pseudopotential LB model has been quite popular because of automatic phase separation via an inter-particle potential (Frank et al. 2006; Shan and Chen 1993). Gong and Cheng (2015) combined multiphase LBM with an energy equation model to simulate the liquid–vapor phase change.

In the pseudopotential LB approach (Chen et al. 2014; Li et al. 2015), the liquid–vapor interfaces can naturally arise, deform, and migrate without using the interface tracking or interface capturing techniques and hence a big advantage compared to the existing methods.

In the future, ever-increasing computational power and newer computational techniques will enable fundamental understanding of turbulent two-phase flows, which will underpin the development of new boiling heat transfer models. Combining direct numerical simulation (DNS) of turbulence with interface tracking methods for simulating turbulent boiling flows is still not feasible. The computational cost of direct numerical simulation increases linearly with Reynolds number added with this; the complex topological changes of the interface along with its own computational difficulties make it a daunting task. DNS of two-phase flows is understandably still not foreseeable at the moment, but when it is developed it will be the ultimate numerical tool for bridging the gap between scales of simulation and enable decisive advancement of our understanding of the boiling processes.

4 Summary

A review of different techniques and models for simulating boiling flows has been presented. Simulation of boiling and two-phase heat transfer poses a number of challenges, and in this brief review, we have tried to show how the challenges were addressed by different researchers using different techniques.