Keywords

1 Introduction

Every day, a large amount of wastes are produced by mining industry. It is a great challenge to adequately manage these mine wastes. For most case, they are deposited on surface and constitute potential sources of environmental (e.g. acid mine drainage) and geotechnical problems (failure of tailings dams) [1]. However, mine wastes can be used as filling material to fill underground mined-out spaces (stopes). This practice, known as underground mine backfilling, can improve ground stability, increase ore recovery and decrease the amount of mine wastes to be deposited on surface. The environmental impact from mining industry can thus be reduced.

An important issue of mine backfilling is to have a safe and economic design of barricade, a confining structure built at the base of stope near the draw-point to hold the fresh slurried backfill in the stope. Failures of barricade in several mines have been reported and often lead to serious consequences. Subsequently, care is needed to the stability and design of barricades. This requires a pressure estimation in backfilled stopes, which needs a full understanding of the hydro-mechanics behavior of the slurried backfill placed in mine stopes.

When a slurried backfill is discharged into a mine stope, the solid particles tend to settle down under the action of their own weight. The backfill thus tends to become denser while the pore water tends to be expelled out of the slurry. As mine backfill made of full tailings usually contains a large portion of fine particles, the permeability is usually small. The pore water cannot drain out quickly and excess pore water pressure (PWP) is generated. In most case, the total PWP at the moment of slurry pour can be as high as the vertical total stress based on the overburden of the backfill. The effective stresses are absent. The vertical and horizontal total stresses are identical and equal to the PWP. The pressures are called hydrostatic, geostatic or isostatic pressure based on overburden.

With time, the drainage and dissipation of excess PWP take place. When the process reaches a degree where the particles contact each other, effective stress can be developed. This drainage and dissipation of the excess PWP are called self-weight consolidation. Gibson [2] is probably the first one to evaluate the evolution of the PWP associated with the self-weight consolidation of accreting deposition of slurried backfill. As the Gibson [2] model is one dimensional consolidation theory without consideration of the effective stresses, it has been directly used to evaluate the pressure evolution in mine backfilled stopes [3, 4].

However, when the dissipation of the excess PWP reaches a degree where the particles of the backfill touch each to other, effective stresses start to develop, leading to the generation of shear stresses along the fill-wall contacts. The shear stresses along the fill-wall contacts tend to decrease the stresses in the backfilled opening, resulting in stresses and pressures less than those based on the overburden solution. This phenomenon is known as arching effect.

The arching theory has been used to estimate the pressures of backfill placed in mine stopes. More representative conditions of mine backfilled stopes have also been considered in the arching theory, such as the 3D geometry [5] and non-uniform stress distribution across the stope width [6]. However, most of the previous studies involving arching effect were conducted by considering dry backfill. Only a few studies were reported by considering submerged backfill in stopes with hydrostatic pressure, a state corresponding to the final steady state at the end of the drainage and dissipation of the excess PWP [7].

The brief literature review given above indicates that most of the existing works on pressure estimation in backfilled openings are devoted to the two extreme cases, either to the beginning or to the end of the self-weight consolidation process. No consideration was given to the intermediate state, in which the excess PWP dissipation and arching development jointly occur.

In this paper, the self-weight consolidation and arching effect during the placement of slurried backfill are jointly considered in evaluating the stresses in backfilled stopes. The excess PWP is first calculated by using the truly analytical solution of the Gibson (1958) model [2], developed by Zheng et al. [4]. The PWP is then introduced into the arching solution to obtain the effective and total stresses. The proposed solution is validated by numerical modeling conducted with PLAXIS 2D.

2 Proposed Solution

2.1 Self-weight Consolidation of Accreting Deposition of Slurried Backfill

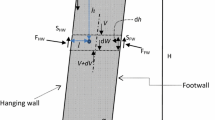
Figure 1 shows a mine stope (with impervious surrounding rock walls) being continuously filled with a slurried backfill. The backfill thickness increases at a filling rate of m (m/h). On the figure, h is the current thickness of the backfill at a given time t (i.e. h = mt); H is the final thickness at the end of deposition; B is the width of the stope; x and y are the abscissa and ordinate of the coordinate system, respectively; l is the depth of a layer element to be considered in the solution development; V is the vertical force on the top of the layer element; W is the weight of the layer element, C and S are the compressive and shear forces on the side of the layer element, respectively.

Fig. 1.
figure 1

Accreting deposition of slurried material in a mine stope with a horizontal layer element.

Full size image

Gibson (1958) gave the following equation to describe the self-weight consolidation of an accreting deposition of slurried backfill:

$$ c_{v} \frac{{\partial^{2} u}}{{\partial y^{2} }} = \frac{\partial u}{\partial t} - \gamma^{\prime}\frac{dh}{dt} $$
(1)

where u (kPa) is the excess PWP, cv (m2/h) is the consolidation coefficient, t (h) is the deposition time, γ′ (kN/m3) is the submerged unit weight of the backfill.

Solving Eq. (1) leads to the following equation (Gibson [2]):

$$ u = \gamma^{\prime}mt - \gamma^{\prime}E(\pi c_{v} t)^{{ - \frac{1}{2}}} \exp \left( {\frac{{ - y^{2} }}{{4c_{v} t}}} \right) $$
(2)

where

$$ E = \int_{0}^{\infty } {\xi \tanh \left( {\frac{m\xi }{{2c_{v} }}} \right)} \times \cosh \left( {\frac{y\xi }{{2c_{v} t}}} \right) \times \exp \left( { - \frac{{\xi^{2} }}{{4c_{v} t}}} \right)d\xi $$
(3)

and ξ(m) is an integral variable (0 < ξ < ∞).

The derivation of excess PWP leads to an expression as follows:

$$ \frac{du}{dy} = - \gamma^{\prime}(\pi c_{v} t)^{{ - \frac{1}{2}}} \exp \left( {\frac{{ - y^{2} }}{{4c_{v} t}}} \right) \times \left[ {\left( {\frac{ - y}{{2c_{v} t}}} \right) \times E + F} \right] $$
(4)

where

$$ F = \int_{0}^{\infty } {\xi \tanh \left( {\frac{m\xi }{{2c_{v} }}} \right)} \times \sinh \left( {\frac{y\xi }{{2c_{v} t}}} \right) \times \left( {\frac{\xi }{{2c_{v} t}}} \right) \times \exp \left( { - \frac{{\xi^{2} }}{{4c_{v} t}}} \right)d\xi $$
(5)

The integral in Eqs. (3) or (5) can be approximated by a summation of series proposed by Goodwin [8]:

$$ \int_{ - \infty }^{\infty } {g(z) \times \exp ( - z^{2} )dz = h_{0} } \sum\limits_{n = - \infty }^{\infty } {g(nh_{0} )\exp ( - n^{2} h_{0}^{2} )} $$
(6)

in which, g is a generic function of a variable z; n is a series number; h0 is step interval of z. Goodwin [8] has shown that high accuracy approximation can be obtained as the value of n is large enough and h0 is taken between 0 and 1.

Equations (3) and (5) can then be rewritten as follows:

$$ E = \frac{{h_{0} }}{2}\sum\limits_{n = - \infty }^{\infty } {4c_{v} } t \times (nh_{0} ) \times \tanh \left( {\frac{{mnh_{0} \sqrt t }}{{\sqrt {c_{v} } }}} \right) \times \cosh \left( {\frac{{ynh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \exp ( - n^{2} h_{0}^{2} ) $$
(7)
$$ F = \frac{{h_{0} }}{2}\sum\limits_{n = - \infty }^{\infty } {4c_{v} } t \times (nh_{0} ) \times \tanh \left( {\frac{{mnh_{0} \sqrt t }}{{\sqrt {c_{v} } }}} \right) \times \sinh \left( {\frac{{ynh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \left( {\frac{{nh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \exp ( - n^{2} h_{0}^{2} ) $$
(8)

With Eqs. (2) and (7), the excess PWP, u, can be expressed as follows:

$$ u = \gamma^{\prime}mt - \gamma^{\prime}(\pi c_{v} t)^{{ - \frac{1}{2}}} \exp \left( {\frac{{ - y^{2} }}{{4c_{v} t}}} \right) \times \frac{{h_{0} }}{2}\sum\limits_{n = - \infty }^{\infty } {4c_{v} } t \times (nh_{0} ) \times \tanh \left( {\frac{{mnh_{0} \sqrt t }}{{\sqrt {c_{v} } }}} \right) \times \cosh \left( {\frac{{ynh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \exp ( - n^{2} h_{0}^{2} ) $$
(9)

Equation (9) is the analytical solution of Gibson [2] model proposed by Zheng et al. [4]. In most case, a stable result of u can be obtained when the value of h0 is taken as 0.3 and n is in the range of −91 to 91.

With Eqs. (4), (7) and (8), the du/dy can be expressed as follows:

$$ \begin{aligned} \frac{du}{dy} = - \gamma^{\prime}(\pi c_{v} t)^{{ - \frac{1}{2}}} \exp \left( {\frac{{ - y^{2} }}{{4c_{v} t}}} \right) \times [\left( {\frac{ - y}{{2c_{v} t}}} \right) \times \frac{{h_{0} }}{2}\sum\limits_{n = - \infty }^{\infty } {4c_{v} } t \times (nh_{0} ) \times \tanh \left( {\frac{{mnh_{0} \sqrt t }}{{\sqrt {c_{v} } }}} \right) \times \cosh \left( {\frac{{ynh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \exp ( - n^{2} h_{0}^{2} ) + \\ \frac{{h_{0} }}{2}\sum\limits_{n = - \infty }^{\infty } {4c_{v} } t \times (nh_{0} ) \times \tanh \left( {\frac{{mnh_{0} \sqrt t }}{{\sqrt {c_{v} } }}} \right) \times \sinh \left( {\frac{{ynh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \left( {\frac{{nh_{0} }}{{\sqrt {c_{v} t} }}} \right) \times \exp ( - n^{2} h_{0}^{2} )] \\ \end{aligned} $$
(10)

Equations (10) will be used in the next section to evaluate the stresses in backfilled stopes during the placement of backfill by considering the excess PWP dissipation.

2.2 Arching Consideration

Considering the equilibrium of the isolated layer element (Fig. 1) yields

$$ dV + 2S = W $$
(11)

The vertical force V can be calculated as follows by assuming a uniformly distributed vertical stress σv across the width of stope

$$ V = \sigma_{v} B $$
(12)

The weight of the layer element is expressed as follows

$$ W = \gamma_{sat} B\,{\text{d}}l $$
(13)

where γsat (kN/m3) is the unit weight of the saturated backfill; dl is the thickness of the layer element.

The shear force acting on the side of the layer element can be calculated by using the Mohr-Coulomb criterion

$$ S = \sigma^{\prime}_{h} \,\tan \,\delta^{\prime}\,dl = K\sigma^{\prime}_{v} \,\tan \,\phi^{\prime}\,dl $$
(14)

where \( \sigma^{\prime}_{v} \) (kPa) is the vertical effective stress; \( \sigma^{\prime}_{\text{h}} \) (kPa) is the horizontal effective stress; δ′ (°) is the effective friction angle along the interface between the backfill and rock wall, which is assumed to be equal to the effective internal frictional angle of the backfill ϕ′(°); K is the earth pressure coefficient, which is usually taken as the Rankine’s active earth pressure coefficient Ka ( = (1 − sinϕ′)/(1 + sinϕ′)) or Jaky’s at-rest earth pressure coefficient K0 (= 1 − sinϕ′) in mine backfilled stopes.

Introducing Eqs. (12), (13) and (14) into Eq. (11) leads to

$$ \frac{{d\sigma^{\prime}_{v} }}{dl} + \frac{{2K\,\tan \,\phi^{\prime}}}{B}\sigma^{\prime}_{v} = \gamma^{\prime} - \frac{du}{dl} $$
(15)

The vertical effective stress can be solved from Eq. (15) as follows

$$ \sigma_{v}^{'} = e^{{ - \frac{{2K\,\tan \,\phi^{'} }}{B}l}} \left[ {\int {(\gamma^{'} - \frac{du}{dl})e^{{\frac{{2K\,\tan \,\phi^{'} }}{B}l}} } dl + A} \right] $$
(16)

where A is an arbitrary constant.

Considering the boundary condition \( \sigma^{\prime}_{v} \) = 0 at l = 0 leads to

$$ \sigma^{\prime}_{v} = e^{{ - \frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} \int_{0}^{l} {\left( {\gamma^{\prime} - \frac{du}{dy}} \right)e^{{\frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} } dl $$
(17)

Considering l = h − y and du/dl = −du/dy, Eq. (17) yields

$$ \sigma^{\prime}_{v} = e^{{ - \frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} \int_{0}^{l} {\left( {\gamma^{\prime} + \frac{du}{dy}} \right)} e^{{\frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} dl $$
(18)

Equation (18) constitutes a solution to calculate the vertical effective stress within the slurried backfill during the accreting deposition. The horizontal effective stress can be calculated as \( \sigma^{\prime}_{\text{h}} \) = K\( \sigma^{\prime}_{\text{h}} \), while the vertical and horizontal total stresses can then be calculated as follows:

$$ \sigma_{v} = \sigma^{\prime}_{v} + u + \gamma_{w} l = e^{{ - \frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} \int_{0}^{l} {\left( {\gamma^{\prime} + \frac{du}{dy}} \right)} e^{{\frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} dl + u + \gamma_{w} l $$
(19)
$$ \sigma_{h} = \sigma^{\prime}_{h} + u + \gamma_{w} l = ke^{{ - \frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} \int_{0}^{l} {\left( {\gamma^{\prime} + \frac{du}{dy}} \right)} e^{{\frac{{2K\,\tan \,\phi^{\prime}}}{B}l}} dl + u + \gamma_{w} l $$
(20)

3 Validation of the Proposed Solution by PLAXIS 2D

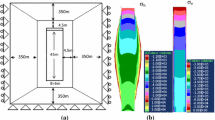
To evaluate the validation of the proposed solution, numerical simulations were conducted with PLAXIS2D to evaluate the stresses distribution in a backfilled stope.

Figure 2 shows the numerical model of a mine backfilled stope. The stope has a width of B = 4 m and filled at a filling rate of m = 0.5 m/h to a final height of H = 12 m. The slurried backfill is cohesionless and obeys the Mohr-Coulomb criterion; its properties are shown in Fig. 2. The impermeable surrounding rock is elasto-plastic, obeying the Mohr-Coulomb criterion. Its properties are shown in the figure.

Fig. 2.
figure 2

Numerical model of a backfilled stope filled with a slurried backfill.

Full size image

As shown in Fig. 2, the symmetry plane was taken into account and the numerical simulations were conducted by considering half of the model. The upper outer boundary of the numerical model is left free in all directions. The bottom of outer boundary is fixed in the horizontal and vertical directions. The two vertical side boundaries are allowed to freely move in the vertical direction but fixed in the horizontal direction. Drainage is only allowed through the top surface of each newly added backfill layer.

An initial stress is first obtained in the rock. The excavation is conducted to form the mine stope, which is then filled with backfill in layers. In practice, the filling is continuous. This can only be approximated in PLAXIS 2D by instantaneous additions of thin layers of backfill. The backfill thickness should be small enough to represent the continuous deposition. Here, the stop is filled to a final height of 12 m with layer thickness of 0.4 m. The waiting time between two consecutive layers is 0.8 h with m = 0.5 m/h.

Figure 3 shows the distribution of the excess PWP (Fig. 3a), effective and total (Fig. 3b) stresses along the height of the backfilled stope at the end of filling operation (at t = 24 h), obtained with the PLAXIS 2D and calculate with the proposed solution (Eqs. 9, 18, 19, and 20) by considering K = Ka. The good agreements between the pressures and stresses obtained by the proposed solution using K = Ka and the numerical modeling with PLAXIS 2D indicate that the proposed solution is validated. One can also see that the u obtained by the numerical modeling and calculated with the proposed solution are much smaller than that based on the isostatic pressure solution. This indicates the occurrence of significant dissipation of the excess PWP during the filling operation. In addition, the occurrence of arching effect during the placement of the backfill is illustrated by the non-negligible effective stresses and the calculated total stresses smaller than the isostatic pressure based on the overburden pressure shown in Fig. 3b. Neglecting the excess PWP dissipation and arching effect may thus result in overly conservative and uneconomic design of barricades.

Fig. 3.
figure 3

Distribution of the (a) excess PWP, (b) effective and total stresses along the height of the backfilled stope at the end of the filling operation, obtained by numerical modeling with PLAXIS 2D and calculated with the proposed solution (Eqs. 9, 18, 19, and 20) using K = Ka.

Full size image

4 Conclusion

The safe and economic design of backfill barricades is largely dependent on the reliability and accuracy of the stress estimation in backfilled stopes and pressures on barricades. In this paper, a new solution has been proposed to evaluate the stresses in backfilled stopes during the accreting deposition on an impervious base. Self-weight consolidation and arching effect are jointly considered by calculating the excess PWP in the backfill using the analytical solution of Gibson (1958) model first and then introducing into the arching solution. The proposed solution is validated by numerical simulations conducted with PLAXIS 2D. It thus constitutes a useful tool to calculate the stresses in backfilled stopes. The proposed solution can also be used to evaluate the influence of some key factors (e.g., filling rate, consolidation coefficient, backfill final height, etc.) on the stresses development in backfilled stopes during the filling.