Glucose Regulation in Diabetes Patients Via Insulin Pump: A Feedback Linearisation Approach

Abstract

The primary objective of the paper is to design a nonlinear control technique for a nonlinear intravenous model of Type 1 diabetes mellitus (T1DM) patient. Input–output feedback linearisation is utilised for deriving the nonlinear control law based on a modified version of Bergman’s minimal model augmented with the dynamics of the insulin pump and the meal disturbance. The results depict that the proposed control technique avoids severe hypoglycaemia and postprandial hyperglycaemia in the presence of exogenous meal disturbance as well as parametric uncertainty within a population of 100 virtual T1DM patients (inter-patient variability). The efficacy of the proposed control technique is investigated through variability grid analysis.

1 Introduction

Due to immune-mediated depredation of the pancreatic $\beta$-cells resulting in negligible secretion of insulin, blood glucose concentrations cannot be tightly controlled within the safe range (50–180 mg/dl) by the pancreas leading to events of hyperglycaemia (>180 mg/dl) or severe hypoglycaemia (<50 mg/dl) [11]. While hyperglycaemia is associated with long-term health diseases such as heart disease, blindness, kidney failure and nerve damage, hypoglycaemia has the immediate effect that may lead to diabetic coma leading to death [3, 6]. The dependency of T1DM patients on exogenous insulin infusions either through multiple daily insulin injections or insulin infusion pump (IIP) results in hyperglycaemic and hypoglycaemic events. The role of Artificial Pancreas (AP) system is vital in addressing these issues via closed-loop control of the blood glucose concentration that is achieved through sensing the blood glucose by continuous glucose monitoring (CGM) systems and infusing insulin continuously through IIP as determined by the control algorithm [7]. Despite the advances in technology and communications in AP systems, important control challenges exist due to: (i) huge time lags in insulin action, insulin absorption and glucose sensing dynamics, (ii) exogenous disturbances like meals, exercise, stress and sleep and (iii) parametric variability both within a population (inter-patient variability) and within the same T1DM patient (intra-patient variability) [5]. The physiologically based mathematical models of T1DM patients can be broadly categorised into the intravenous models [4] and the subcutaneous models [6, 15] depending upon whether the glucose sensing and insulin infusion route are intravenous (directly into the veins) or subcutaneous (under the skin). In this current work, we have considered popular Bergman’s minimal model (BMM) that is not only simplistic in structure but also represents the glucose–insulin regulatory system quite accurately, which have important applications in ICU medications and treatment of diabetes ketoacidosis [20].

Various control algorithm like proportional–integral–derivative (PID), model predictive control (MPC) and fuzzy logic control have been proposed for maintaining the plasma glucose concentration in the safe range in T1DM patients are discussed in [11]. Different variants of sliding mode control (SMC) techniques like back steeping SMC [19], Higher order SMC [14, 16] and super twisting controller [1] were designed for Bergman’s minimal model where the issue of inter-patient variability was addressed. It is important to note that the design of the control algorithms based on BMM as reported in [1, 8, 9, 14, 16, 19] did not consider the dynamics of IIP. The novelty in this paper is the consideration of more realistic scenario for AP system by augmenting the pump dynamics [12, 13] to the modified Bergman’s minimal model [2], where the parametric variability appearing due to inter-patient variability in T1DM patients is addressed. The design of the nonlinear controller avoids the linearization of the nonlinear dynamics as in [9, 12, 13], thus preserving the nonlinear characteristics of the system. Since control variability grid analysis (CVGA) [18] is a significant tool for the performance assessment of closed-loop control techniques in addressing inter-patient variability, unlike the above-mentioned control algorithms [1, 8, 9, 12,13,14, 16, 19], here CVGA was performed for 100 virtual T1DM patients.

The paper is structured into four sections. Section 2 deals with the modelling of the glucose–insulin regulatory system of T1DM patients as well as the design of the control law. The simulation results investigating the effectiveness of the proposed scheme is provided in Sect. 3. Section 4 contains the concluding remarks and future scope of the proposed work.

2 Design Methodology

In this section, an integrated mathematical model that is essentially a modification of the BMM is introduced where the insulin pump dynamics, as well as the meal disturbance dynamics, are augmented. The first subsection deals with the mathematical modelling of T1DM patients. The design of the control law is discussed in the succeeding subsection.

2.1 Mathematical Model for Glucose–Insulin Regulatory System

In this present work, the BMM [4] is chosen for the model-based controller design. A modified version of the BMM is considered here as in [2]. Further, the modified model is augmented with the insulin pump dynamics as discussed below

$$\begin{aligned} \dot{{ G}}_{p}({ t})= & {} -{ I}_{r}({ t}){ G}_{p}({ t})-{ c}_{1}{ G}_{p}({t}) +{c}_{1}{G}_{b}+{D}({t})\end{aligned}$$

(1)

$$\begin{aligned} \dot{{I}}_{r}({t})= & {} -{c}_{2}{I}_{r}({t}) +{c}_{3}{I}_{p}({t})-{c}_{3}{I}_{b},\end{aligned}$$

(2)

$$\begin{aligned} \dot{{I}}_{p}({t})= & {} -{c}_{4}{I}_{p}({t})+{c}_{4}{I}_{b} +\gamma _{p}[{G}_{p}({t})-{h}_{p}]^{+}{t}, \end{aligned}$$

(3)

where the BGC is represented by ${G}_{p}({t})$, the delayed insulin’s effect on BGC by ${I}_{r}({t})$ (min$^{-1}$) and ${I}_{p}({t})$ ($\upmu$U/ml) denotes the plasma insulin concentration. ${G}_{b}$ and ${I}_{b}$ denote the steady state (basal) value of ${G}_{p}({t})$ and ${I}_{p}({t})$, respectively. The BMM is essentially a compartmental model composed of the dynamics for glucose homeostasis and insulin kinetics as modelled by Eqs. (1)–(3) representing the plasma glucose compartment, the remote insulin compartment and plasma insulin compartments, respectively. The important physiological parameters of glucose–insulin regulatory system can be expressed in terms of the BMM’s parameters [2, 4] directly. The parameter, ${c}_1$ (min$^{-1}$) signifies the insulin-independent glucose utilisation occurring in muscles and liver. Insulin sensitivity is represented by $\frac{{c}_3}{{c}_2}$ ($(\upmu {U}/{ml})^{-1}\hbox {min}^{-1}$) and ${c}_{4}$ (min$^{-1}$) is the rate of degradation of ${I}_{p}({t})$. $\gamma _{p}[{G}_{p}({t})-{h}_{p}]^{+}{t}$ represents the pancreatic actions in maintaining BGC (negligible in T1DM patients). As mentioned in [10], the term D(t) (mg/dl/min) represents the exogenous meal disturbance (the rate at which glucose appears in the plasma glucose compartment) that is modelled by an exponentially decaying function, as follows:

$$\begin{aligned} \dot{{D}}({t})= & {} -{c}_{6} {D}({t}),\quad {c}_6 >0, \end{aligned}$$

(4)

where the parameter ${c}_6$ (min$^{-1}$) represents the time-to-peak glucose following exogenous glucose disturbance.

In this present work, the above-mentioned modified version of the BMM is augmented with a simple first-order linear state-space model that represents the actuator (insulin pump) dynamics, thus enabling us to design a suitable controller for regulating BGC in T1DM patients for a more realistic scenario. As reported in [12, 13], the pump model is represented as

$$\begin{aligned} \dot{{U}}({t})={c}_5[-{U}({t})+ {U}_{c}({t})] \end{aligned}$$

(5)

where $\frac{1}{{c}_5}$ represents the time constant for the pump and ‘U’ is the actual insulin infusion rate as determined by the command input ‘${U}_{c}$’. All the dynamics of the physiological variables of the glucoregulatory system along with the meal disturbance as well as insulin pump dynamics are expressed in a compact form:

$$\begin{aligned} \begin{array}{l} \dot{{x}}_{1_{o}}=-{x}_{1_{o}}{x}_{2_{o}}-{c}_{1}{x}_{1_{o}}+{c}_{1} {G}_{b}+{x}_{5_{o}}\\ \dot{{x}}_{2_{o}}=-{c}_{2}{x}_{2_{o}}+{c}_{3}{x}_{3_{o}}-{x}_{3_{o}}{I}_{b}\\ \dot{{x}}_{3_{o}}= -{c}_4{x}_{3_{o}}+{c}_{4}{I}_{b}+{x}_{4_{o}}\\ \dot{{x}}_{4_{o}}=-{c}_5{x}_{4_{o}}+{c}_5 {U}_{c}\\ \dot{{x}}_{5_{o}}=-{c}_6{x}_{5_{o}} \end{array} \end{aligned}$$

(6)

where, ${x}_{1_{o}}, {x}_{2_{o}}, {x}_{3_{o}}, {x}_{4_{o}}$ and $x_{5_{o}}$ represents ${G}_{p}({t}), {I}_{r}({t}), {I}_{p}({t}), {U}({t})$ and D(t), respectively. The state variable appearing in (6) can be expressed as deviation terms from their equilibrium as reported in [2].

$$\begin{aligned} \begin{array}{l} \dot{{x}}_{1d}=-{c}_{1}{x}_{1d}-({x}_{1d}+{G}_{b}) {x}_{2d}+{x}_{5d} \\ \dot{{x}}_{2d}=-{c}_{2}{x}_{2d}+{c}_{3}{x}_{3d} \\ \dot{{x}}_{3d}=-{c}_{4}{x}_{3d}+{x}_{4d} \\ \dot{{x}}_{4d}=-{c}_{5}{x}_{4d}+{c}_{5}{U}_{c}\\ \dot{{x}}_{5d}=-{c}_{6}{x}_{5d} \end{array} \end{aligned}$$

(7)

where the deviated states $[{x}_{1_{d}}~{x}_{2_{d}}~ {x}_{3_{d}}~{x}_{4_{d}}~{x}_{5_{d}}]^{T}$ are expressed as the difference between the original states $[{x}_{1_{o}} ~{x}_{2_{o}} ~{x}_{3_{o}}~ {x}_{4_{o}}~ {x}_{5_{o}}]^{T}$ and their equilibrium $[{x}_{1_{e}}={G}_{b}~ {x}_{2_{e}}=0 ~ {x}_{3_{e}}={I}_{b} ~ {x}_{4_{e}} =0~ {x}_{5_{e}}=0]^{T}$ are given as follows:

$$\begin{aligned} \left[ \begin{array}{ccccc} {x}_{1_{o}}&{x}_{2_{o}}&{x}_{3_{o}}&{x}_{4_{o}}&{x}_{5_{o}} \end{array} \right] ^{T}=\left[ \begin{array}{ccccc} {x}_{1_{e}}&{x}_{2_{e}}&{x}_{3_{e}}&{x}_{4_{e}}&{x}_{5_{e}} \end{array} \right] ^{T}+\left[ \begin{array}{ccccc} {x}_{1_{d}}&{x}_{2_{d}}&{x}_{3_{d}}&{x}_{4_{d}}&{x}_{5_{d}} \end{array} \right] ^{T}, \end{aligned}$$

(8)

We can rewrite (7) as in the compact form as,

$$\begin{aligned} \dot{\varvec{x}}_{\varvec{d}}({t})=\varvec{f}(\varvec{x}_{\varvec{d}}, t)+ \varvec{g}(\varvec{x}_{\varvec{d}},t){U}_{c}({t}), \end{aligned}$$

(9)

$$ \text {where},\, \varvec{f}(\varvec{x}_{\varvec{d}},t)= \begin{bmatrix} \begin{array}{l} -{c}_{1}{x}_{1d}-\left( {x}_{1d}+{G}_{b}\right) {x}_{2d}+{x}_{5d}\\ -{c}_{2}{x}_{2d}+{c}_{3}{x}_{3d}\\ -{c}_{4}{x}_{3d}+{x}_{4d}\\ -{c}_{5} {x}_{4d}\\ -{c}_{6}{x}_{5d} \end{array} \end{bmatrix}, \varvec{g}(\varvec{x}_{\varvec{d}},t)= \begin{bmatrix} \begin{array}{c} 0 \\ 0 \\ 0\\ {c}_5\\ 0 \end{array} \end{bmatrix} ,\text {and output} $$

$$\begin{aligned} {y}({t})={h}(\varvec{x}_{\varvec{d}},t)={\varvec{C}} \varvec{x}_{\varvec{d}},~~{\varvec{C}}=\left[ 1 ~0~ 0~ 0~ 0~\right] \end{aligned}$$

(10)

2.2 Feedback Linearisation Control Technique

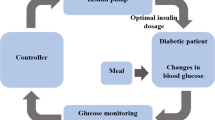
In this work, a nonlinear control law is proposed based on the input–output feedback linearisation. A conceptual block diagram of the proposed control technique is demonstrated in Fig. 1.

Fig. 1

Feedback linearisation-based nonlinear control

The main idea of this control technique is composed of (i) the choice of appropriate scalar output function and (ii) the linearisation of the input–output mapping of the original nonlinear system by the proposed controller via successive differentiation of the selected output. Here, the output of the system is chosen as ${y}={h}(\varvec{x}_{\varvec{d}})={x}_{1d}$ (BGC) that can be measured directly via CGM devices.

$$\begin{aligned} {y}={h}(\varvec{x}_{\varvec{d}})={x}_{1d} \end{aligned}$$

(11)

The derivatives of the output function are calculated as

$$\begin{aligned} {y}^{(1)}= \mathscr {L}_{\varvec{f}}{h}(\varvec{x}_{\varvec{d}})= {x}_{5d} - {c}_{1}{x}_{1d} - {x}_{2d}({G}_{b} + {x}_{1d}),~~~~\mathscr {L}_{\varvec{g}} \mathscr {L}_{\varvec{f}}{h}(\varvec{x}_{\varvec{d}})=0 \end{aligned}$$

(12)

$$\begin{aligned} {y}^{(2)}=\mathscr {L}_{\varvec{f}}^2{h}(\varvec{x}_{\varvec{d}})=({c}_1 + {x}_{2d}) ({c}_1 {x}_{1d} - {x}_{5d} + {x}_{2d}({G}_{b} + {x}_{1d})) - {c}_6 {x}_{5d} + \end{aligned}$$

$$\begin{aligned} ({G}_{b} + {x}_{1d})({c}_2 {x}_{2d} - {c}_3 {x}_{3d}),~~~~ \mathscr {L}_{\varvec{g}} \mathscr {L}_{\varvec{f}}^{2h}(\varvec{x}_{\varvec{d}})=0 \end{aligned}$$

(13)

$$\begin{aligned}&{y}^{(3)}=\mathscr {L}_{\varvec{f}}^{3h}(\varvec{x}_{\varvec{d}})= {c}_6 {x}_{5d} ({c}_1 + {c}_6 + {x}_{2d}) - ({c}_2 {x}_{2d} - {c}_3 {x}_{3d}) ({c}_1 {x}_{1d} - {x}_{5d} + ({G}_{b} + {x}_{1d})\nonumber \\&({c}_1 + {x}_{2d}) + {c}_2 ({G}_{b} + {x}_{1d}) + {x}_{2d} ({G}_{b} + {x}_{1d})) -{c}_3 ({G}_{b} + {x}_{1d}) ({x}_{4d} - {c}_4 {x}_{3d}) -({c}_1 {x}_{1d}\nonumber \\&\quad \qquad \qquad \qquad \qquad - {x}_{5d} + {x}_{2d} ({G}_{b} + {x}_{1d})) ({c}_2 {x}_{2d} - {c}_3 {x}_{3d} + ({c}_1 + {x}_{2d})^2) \end{aligned}$$

(14)

$$\begin{aligned} \mathscr {L}_{\varvec{g}} \mathscr {L}_{\varvec{f}}^{3h}(\varvec{x}_{\varvec{d}}) =-{c}_3 {c}_5 ({G}_{b} + {x}_{1d}) \ne 0 \end{aligned}$$

(15)

$$\begin{aligned} {y}^{(4)}&=\mathscr {L}_{\varvec{f}}^{4h}(\varvec{x}_{\varvec{d}}) = (({c}_1 + {x}_{2d})({c}_{2}{x}_{{2d}} - {c}_{3}{x}_{{3d}} + ({c}_1 + {x}_{2d})^2)\nonumber \\&\quad + ({c}_2 {x}_{2d} - {c}_3 {x}_{3d}) ({2c}_1 + {c}_2 + {2x}_{2d})\nonumber \\&\quad + {c}_3({x}_{4d} - {c}_4 {x}_{3d})) ({c}_1 {x}_{1d} - {x}_{5d} + {x}_{2d} ({G}_{b} + {x}_{1d})) \nonumber \\&\quad + ({c}_2 {x}_{2d} - {c}_3 {x}_{3d})(({G}_{b} + {x}_{1d})({c}_2 {x}_{2d} - {c}_3 {x}_{3d} + ({c}_1 + {x}_{2d})^2)\nonumber \\&\quad + (2 {G}_{b} + 2 {x}_{1d}) ({c}_2 {x}_{2d} - {c}_3 {x}_{3d}) - {c}_6 {x}_{5d} + ({c}_1 {x}_{1d}\nonumber \\&\quad - {x}_{5d} + {x}_{2d} ({G}_{b} + {x}_{1d})) (2 {c}_1 + {c}_2 + 2 {x}_{2d})\nonumber \\&\quad + {c}_2 ({c}_1 {x}_{1d} - {x}_{5d} + ({G}_{b} + {x}_{1d}) ({c}_1 + {x}_{2d}) + {c}_2 ({G}_{b} +{x}_{1d}) \nonumber \\&\quad + {x}_{2d} ({G}_{b} + {x}_{1d}))) + ({x}_{4d} - {c}_4 {x}_{3d}) ({c}_3 ({c}_1 {x}_{1d} - {x}_{5d} + {x}_{2d} ({G}_{b} + {x}_{1d}))\nonumber \\&\quad + {c}_3 ({c}_1 {x}_{1d} - {x}_{5d} + ({G}_{b} + {x}_{1d}) ({c}_1 + {x}_{2d}) + {c}_2 ({G}_{b} + {x}_{1d}) + {x}_{2d}({G}_{b} + {x}_{1d}))\nonumber \\&\quad + {c}_3 {c}_4 ({G}_{b} + {x}_{1d})) - {c}_{6}{x}_{5d} ({2c}_2 {x}_{2d} - 2 {c}_3 {x}_{3d} + {c}_6 ({c}_1 + {c}_6 + {x}_{2d})\nonumber \\&\quad + ({c}_1 + {x}_{2d})^2) + {c}_3 {c}_5 {x}_{4d} ({G}_{b} + {x}_{1d}) \end{aligned}$$

(16)

where ${y}^{({i})}, {i}=1,{2}\ldots ,4$ denote the successive differentiation terms of the output function (10), respectively. Since $\mathscr {L}_{\varvec{g}} \mathscr {L}_{\varvec{f}}^{3h}({\varvec{x}}_{d}) \ne 0$ the relative degree of the system (9) is $\rho =4$. Clearly, since the relative degree ($\rho =4$) is less than the system’s order (${n}=5$), the system (9) can be expressed in the in the transformed coordinate as follows:

$$\begin{aligned} \dot{\varvec{\zeta }}={\varvec{A}}_{\varvec{\zeta }} \zeta +{\varvec{B}}_{\varvec{\zeta }}{v} \end{aligned}$$

(17)

$$\begin{aligned} \dot{\varvec{\eta }}=\varvec{f}_{\varvec{0}}(\eta ,\zeta ) \end{aligned}$$

(18)

$$\begin{aligned} {y}={\varvec{C}}_{\varvec{\zeta }} \eta \end{aligned}$$

(19)

where ${\varvec{A}}_{\varvec{\zeta }}=\left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right]$, ${\varvec{B}}_{\varvec{\zeta }}=\left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ \end{array} \right]$ and ${\varvec{C}}_{\varvec{\zeta }}=\big [1~0~0~0\big ]$. In (18), $\dot{\varvec{\eta }}=\varvec{f}_{\varvec{0}}(\eta ,\zeta )=-{p}_6 {x}_{5_{d}}$ (i.e. internal dynamics), with respect to the chosen output (10). The equilibrium point $\eta =0$ is locally asymptotically stable and hence if we can stabilise the transformed system (17) by designing a state-feedback control law ${v}=-{K}\zeta$ [17]. The ${\rho =4}{{th}}$-derivative of the output function is given by

$$\begin{aligned} {y}^{(4)}=\mathscr {L}_{\varvec{f}}^{4}{h}(\varvec{x}_{\varvec{d}}) +\mathscr {L}_{\varvec{g}} \mathscr {L}_{\varvec{f}}^{3}{h}(\varvec{x}_{\varvec{d}}){U}_{c} \end{aligned}$$

(20)

Let us consider the auxiliary control as

$$\begin{aligned} {y}^{(4)}={v} \end{aligned}$$

(21)

Then, the actual controller expression can be computed from (20) using (21) as follows:

$$\begin{aligned} {U}_{c}=\frac{-\mathscr {L}_{\varvec{f}}^\rho {h}(\varvec{x}_{\varvec{d}})+{v}}{\mathscr {L}_{\varvec{g}}\mathscr {L}_{\varvec{f}}^{\rho -1} {h}(\varvec{x}_{\varvec{d}})} \end{aligned}$$

(22)

The auxiliary control input ‘v’ can be designed as

$$\begin{aligned} {v}=-{k}_{4}{y}^{(3)}-{k}_{3}{y}^{(2)}-{k}_{2} {y}^{(1)}-{k}_{1}{y} \end{aligned}$$

(23)

such that the resulting output dynamics

$$\begin{aligned} {y}^{(4)}=-{k}_{4}{y}^{(3)}-{k}_{3}{y}^{(2)}-{k}_{2} {y}^{(1)}-{k}_{1}{y} \end{aligned}$$

(24)

is linear and time-invariant with the positive constants ${k}_1, {k}_2, {k}_3$ and ${k}_4$ chosen such that the characteristic polynomial given below is Hurwitz.

$$\begin{aligned} \lambda ^4+ {k}_4\lambda ^3+{k}_3\lambda ^2+{k}_2\lambda +{k}_1=0 \end{aligned}$$

(25)

The characteristic polynomial (25) is derived from the fact that the output dynamics can be expressed in a matrix form as follows:

$$\begin{aligned} \dot{\zeta }={A}_{cl}\zeta \end{aligned}$$

(26)

where

$$\begin{aligned} \zeta =\big [{y}~{y}^{(1)}~{y}^{(2)}~{y}^{(3)}\big ]^{T},~~ {A}_{cl}= \left[ \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ -{k}_1 &{} -{k}_2 &{} -{k}_3 &{} -{k}_4 \\ \end{array} \right] \end{aligned}$$

(27)

The exponential convergence of the output trajectories to the origin is guaranteed by the Routh–Hurwitz criterion. From the Routh–Hurwitz criterion, it is obtained that if the inequality

$$\begin{aligned} {k}_4{k}_3>{k}_2 \end{aligned}$$

(28)

holds then the matrix ${A}_{cl}$ is Hurwitz and

$$\lim _{{t}\rightarrow 0} \zeta =0$$

with exponential rate of convergence.

3 Simulation Results

In this section, the simulation studies are carried out for the performance assessment of the proposed feedback linearisation based nonlinear control technique for regulating plasma glucose concentration in T1DM patients for the augmented minimal model. The T1DM patient is considered to be in the hyperglycaemic state (${x}_{1_{o}}=230\,\hbox {mg}/\hbox {dl}$) with no prior exogenous insulin infusions that is reflected by the initial conditions ${x}_{2_{o}} = 0~ \hbox {min}^{-1}$, ${x}_{3_{o}} = 7~{mU}/{l}$ and ${x}_{4_{o}} = 0~\hbox {mU}/\hbox {l}$, with high exogenous meal disturbance ${x}_{5_{o}}= 10$ mg/dl/min. The BMM’s parameter values are considered as in Table 1. The controller gains ${k}_1=0.00009, {k}_2=0.0058, {k}_3=0.15$ and ${k}_4=4.5$ are chosen heuristically for the adjustment in the insulin dosages, u(t) such that the control objectives are satisfied.

Table 1 Nominal value of the parameters [2, 13]

Fig. 2

Plasma glucose concentration of treated and untreated patient

It is evident from Fig. 2 that the blood glucose level stays at the hyperglycaemic state in the absence of exogenous insulin infusion, whereas the blood glucose level is brought down below 180 mg/dl within 150 min thereby avoiding postprandial hyperglycaemia and hypoglycaemia. The external insulin infusion by the insulin pump as determined by the control command ${U}_{c}$ is depicted in Fig. 3.

Fig. 3

Exogenous insulin infusion U(t) determined by the insulin pump

Finally, to investigate the controller’s robustness to parametric uncertainty representing inter-patient variability, CVGA [18] is carried out. CVGA is essentially the grid representation of the maximum (Y-axis) and minimum (X-axis) blood glucose variations of a virtual T1DM patient during the whole simulation period. 100 numerical simulations are carried out with random parameters with $\pm 10\%$ variation from the nominal value specified in Table 1 and with the initial conditions ${x}_{1_{o}}=80\,\hbox {mg}/\hbox {dl},{x}_{2_{o}}=0\,\hbox {min}^{-1}, {x}_{3_{o}}=7\,\hbox {mU}/\hbox {l}, {x}_{4_{o}}=0 \hbox {mU/l/min}, {x}_{5_{o}} =0\,\hbox {mg/dl/min}$ and with an administration of meal disturbance of 10 mg/dl/min at the 100th min. Figure 4 elucidates that all the black dots corresponding to T1DM subjects are confined to the grid B (green zone), thereby ensuring no events of hypoglycaemia during the whole simulation period.

Fig. 4

Control variability grid analysis of 100 closed-loop responses. Each black dot corresponds to 400 min long closed-loop simulation for a single T1DM patient

4 Conclusion

A feedback linearisation technique-based nonlinear control law is designed for the plasma glucose regulation problem of an augmented intravenous modified minimal model of T1DM patient by considering the insulin pump dynamics. The closed-loop performance under inter-patient variability ($\pm 10\%$) is investigated. Occurrences of prolonged hyperglycaemia, as well as hypoglycaemia, are completely avoided as validated by the simulation studies. Despite the parametric uncertainty, the controller is able to maintain the plasma glucose of 100 random virtual T1DM patients in the safe range (50–180 mg/dl) as confirmed by control variability grid analysis plot. Although the proposed controller can efficiently handle parametric uncertainty of $\pm 10\%$, to deal with larger parametric uncertainty, robust and adaptive controllers need be designed.