A Mathematical Approach to Study the Blood Flow Through Stenosed Artery with Suspension of Nanoparticles

Abstract

The present paper deals with the effects of an overlapping stenosis of a micropolar fluid with nanoparticles in a uniform tube. The governing equations have been linearized. The expressions for impedance and shear stress at wall have been deduced. Effects of various parameters like coupling number, micropolar parameter, Brownian motion parameter, thermophoresis parameter, local temperature Grashof number, and local nanoparticle Grashof number on resistance to the flow and wall shear stress of the fluid are studied. Effect of these parameters on arterial blood flow characteristics are shown graphically and discussed briefly under the influence nanoparticles and streamline patterns have been studied with particular emphasis. It is noticed that impedance enhances with the increase of micropolar parameter, thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number but reduces with the increase of coupling number and Brownian motion parameter. Shear stress at wall increases with coupling number and Brownian motion parameter but decreases with micropolar parameter, thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number.

1 Introduction

The Atherosclerosis or Stenosis is a serious medical issue because most of the deaths are occurred due to cardiovascular diseases. It realized that cardiovascular diseases are closely related with flow characteristics in the blood vessels. One of such diseases is stenosis, which is defined as a partial blockage of the blood vessels due to the cholesterol, cellular waste products and deposits of fatty substances, calcium, and fibrin in the inner lining of an artery. These substances are causes for the blockage of blood flow in an artery. It leads to heart attack and stroke, etc. Mainly in this condition flow behavior is quite different from that in a normal artery and it results into significant changes in blood flow, pressure distribution, wall shear stress, and the impedance (flow resistance). In the view of this, blood flow through the stenosed arteries has become prominent and played a leading role of cardiovascular diseases. Based on this, several researchers investigated the characteristics of blood flow in an artery having stenosis by treating blood as non-Newtonian or Newtonian fluid [1, 2].

Micropolar fluid is a non-Newtonian fluid. Eringen [3] proposed the model of micropolar fluid. The main feature of this fluid is that it takes care of the rotation of fluid particles by means of independent kinematic vector known as micro rotation. Several researchers have investigated stenosis by considering blood as micropolar fluid [4, 5].

Present days, many researchers are concentrated on analysis of nanofluids for various flow geometries. A fluid containing nanoscaled particles is called as nanofluid. Nanofluid particles are added to the fluids having low thermal conductivity to increase the thermal conductivity of the fluids. Choi [6] was the first person to introduce the nanofluids. Micropolar fluid having nanoparticles through peristaltic transport in small intestines was studied by Akbar et al. [7].

It is realized that stenosis may develop in series like multiple stenosis or irregular shapes or overlapping. Based on this Srivastava and Shailesh [8] and Maruthi Prasad et al. [9] studied the non-Newtonian arterial blood flow through an overlapping stenosis. However, the effect of overlapping stenosis of a micropolar fluid with nanoparticles has not been studied.

Motivated by the above studies, an effort has been made in this paper to examine the effects overlapping stenosis of a micropolar fluid with nanoparticles has been investigated under the assumption of mild stenosis. The analysis is done analytically. The effect of different relevant parameters on flow variables has been observed through the graphs.

2 Mathematical Formulation

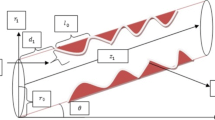
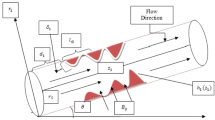
Consider the steady flow of blood through an axially symmetric but radially nonsymmetric overlapping stenosed artery. The geometry of Stenosis can be taken as [8].

$$ \begin{aligned} h & = \frac{R(z)}{{R_{0} }} \\ & = \left\{ {\begin{array}{*{20}l} {1 - \frac{3\delta }{{2R_{0} L_{0}^{4} }}\left[ {11(z - d)L_{0}^{3} - 47(z - d)^{2} L_{0}^{2} + 72(z - d)^{3} L_{0} - 36(z - d)^{4} } \right]} \hfill & {d \le z \le d + L_{0} ,} \hfill \\ {1,} \hfill & {{\text{otherwise}}.} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(1)

where $R_{0} (z)$ the tube radius without stenosis, $R(z)$ is tube radius with stenosis, $L_{0 }$ is stenosis length and d indicates the location of stenosis, and $\delta$ is the maximum stenosis height. Projection of stenosis at the two positions is denoted by z as $z = d + \frac{{L_{0} }}{6},\;z = d + \frac{{5L_{0} }}{6}$, respectively. The critical height is taken as $\frac{3\delta }{4}$ at $z = d + L_{0} /2$, from the origin (Fig. 1).

Fig. 1

Geometry of a uniform tube of circular cross section with overlapping stenosis

Using the following nondimensional quantities

$$ \begin{array}{*{20}c} {\bar{z} = \frac{z}{L}, \overline{L} = \frac{L}{{L_{0} }},\;\bar{u} = \frac{u}{U}, \overline{R} (z) = \frac{R(z)}{{R_{0} }},\;\bar{\delta } = \frac{\delta }{{R_{0} }},\;\bar{u}_{z} = \frac{{u_{z} }}{{u_{0} }},} \\ {\bar{u}_{r} = \frac{{Lu_{r} }}{{u_{0} \delta }},\;\bar{v}_{\theta } = \frac{{R_{0} v_{\theta } }}{{u_{0} }}, \overline{P} = \frac{P}{{\mu UL/R_{0}^{2} }},\bar{q} = \frac{q}{{\pi R_{0}^{2} U}},R_{e} = \frac{{\rho UR_{0} }}{\mu }, } \\ {\bar{h} = \frac{h}{{h_{0} }}, N_{b} = \frac{{(\rho C)_{P} D_{{\overline{B} }} \overline{C}_{0} }}{{(\rho C)_{f} }} ,\quad N_{t} = \frac{{\left( {\rho C} \right)_{P} D_{T} \overline{T}_{0} }}{{\left( {\rho C} \right)_{f} \beta }},G_{r} = \frac{{g\beta \overline{T}_{0} R_{0}^{3} }}{{\gamma^{2} }},\quad B_{r} = \frac{{g\beta \overline{C}_{0} R_{0}^{3} }}{{\gamma^{2} }}.} \\ \end{array} $$

The equations of an incompressible micropolar fluid with nanoparticle under assumption of mild stenosis approximation ($\frac{\delta }{{R_{0} }} \ll 1,\;R_{e}^{*} (2\delta /L_{0} ) \ll 1$, and $2R_{0} /\widetilde{{L_{0} }}(1)$) are defined Maruthi Prasad et al. [10] as

$$ \frac{\partial p}{\partial r} = 0 $$

(2)

$$ \left( {\frac{{\partial^{2} u_{z} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{z} }}{\partial r} + \frac{N}{r}\frac{\partial }{\partial r}\left( {rv_{\theta } } \right)} \right) + (1 - N)\left( {G_{r} \theta_{t} + B_{r} \sigma } \right) = (1 - N)\frac{\partial p}{\partial z} $$

(3)

$$ 2v_{\theta } + \frac{{\partial u_{z} }}{\partial r} - \frac{2 - N}{{m^{2} }}\frac{\partial }{\partial r}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {rv_{\theta } } \right)} \right) = 0 $$

(4)

$$ 0 = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \theta_{t} }}{\partial r}} \right) + N_{b} \frac{\partial \sigma }{\partial r}\frac{{\partial \theta_{t} }}{\partial r} + N_{t} \left( {\frac{{\partial \theta_{t} }}{\partial r}} \right)^{2} $$

(5)

$$ 0 = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \sigma }{\partial r}} \right) + \frac{{N_{t} }}{{N_{b} }}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \theta_{t} }}{\partial r}} \right)} \right) $$

(6)

In which N is the coupling number m is the micropolar parameter, $u_{z}$ is the velocity in the axial direction, $v_{\theta }$ is the micro-rotation in the $\theta$ direction, $\theta_{t}$ is the temperature profile, $\sigma$ is nanoparticle phenomena. $N_{t} ,N_{b} ,B_{r}$, and $G_{r}$ denote thermophoresis parameter, Brownian motion parameter, local nanoparticle Grashof number and local temperature Grashof number.

The relative nondimensional boundary conditions are

$$ \frac{{\partial u_{z} }}{\partial r} = 0,\;\frac{{\partial \theta_{t} }}{\partial r} = 0,\;\frac{\partial \sigma }{\partial r} = 0\quad at\;r = 0 $$

(7)

$$ u_{z} = 0,\;\theta_{t} = 0,\sigma = 0,\;v_{\theta } = 0\quad at\;r = h $$

(8)

$$ u_{z} \;{\text{is}}\;{\text{finite}},\;v_{\theta } \;{\text{is}}\;{\text{flinite}}\;{\text{at}}\;r = 0 $$

(9)

3 Solution

The solutions of the coupled Eqs. (5) and (6) have been solved by using homotropy perturbation method (HPM) as

$$ H\left( {q_{t,} \theta_{t} } \right) = \left( {1 - q_{t} } \right)\left[ {L\left( {\theta_{t} } \right) - L\left( {\theta_{{t_{10} }} } \right)} \right] + q_{t} \left[ {L\left( {\theta_{t} } \right) + N_{b} \frac{\partial \sigma }{\partial r}\frac{{\partial \theta_{t} }}{\partial r} + N_{t} \left( {\frac{{\partial \theta_{t} }}{\partial r}} \right)^{2} } \right] $$

(10)

$$ H\left( {q_{t} ,\sigma } \right) = \left( {1 - q_{t} } \right)\left[ {L\left( \sigma \right) - L\left( {\sigma_{10} } \right)} \right] + q_{t} \left[ {L\left( \sigma \right) + \frac{{N_{t} }}{{N_{b} }}\left( {\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \theta_{t} }}{\partial r}} \right)} \right)} \right]. $$

(11)

Where $q_{t}$ is the embedding parameter which has the range $0 \le q_{t} \le 1$. For our convenience, $L = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right)$ is taken as linear operator. The initial guesses $\theta_{{t_{10} }}$ and $\sigma_{10}$ are defined as

$$ \theta_{{t_{10} }} (r,z) = \left( {\frac{{r^{2} - h^{2} }}{4}} \right),\quad \sigma_{10} (r,z) = - \left( {\frac{{r^{2} - h^{2} }}{4}} \right) $$

(12)

Adopting the same procedure as done by Maruthi Prasad et al. [10], the solution for temperature and nanoparticle phenomena can be written for $q_{t} = 1$ as

$$ \theta_{t} (r,z) = \left( {\frac{{r^{4} - h^{4} }}{64}} \right)\left( {N_{b} - N_{t} } \right) $$

(13)

$$ \sigma (r,z) = - \left( {\frac{{r^{2} - h^{2} }}{4}} \right)\frac{{N_{t} }}{{N_{b} }}. $$

(14)

Substituting Eqs. (13) and (14) in Eq. (3), we get $v_{\theta }$ as,

$$ \begin{aligned} v_{\theta } & = AI_{1} (mr) + BK_{1} (mr) + \frac{(N - 1)}{(2 - N)}\frac{r}{2}\frac{dp}{dz} \\ & \quad + \frac{{G_{r} (1 - N)\left( {N_{b} - N_{t} } \right)}}{(2 - N)}\left[ {\frac{{r^{5} }}{384} + \frac{{r^{3} }}{{16m^{2} }} + \frac{r}{{2m^{4} }} - \frac{{h^{4} r}}{128}} \right] \\ & \quad + \frac{{B_{r} (N - 1)}}{(2 - N)}\frac{{N_{t} }}{{N_{b} }}\left[ {\frac{{r^{3} }}{16} + \frac{r}{{2m^{2} }} - \frac{{h^{2} r}}{8}} \right] \\ \end{aligned} $$

(15)

where $I_{1} (mr)$ and $K_{1} (mr)$ are the modified Bessel functions of first and second order, respectively. Substituting the value of $v_{\theta }$ and using the boundary conditions Eqs. (7)–(9) and expression for velocity $u_{z}$ is

$$ \begin{aligned} u_{z} & = \frac{{(1 - N)}}{{(2 - N)}}\frac{{dp}}{{dz}}\left\{ {\frac{{r^{2} - h^{2} }}{2} + \frac{{Nh}}{{2mI_{1} (mh)}}\left[ {I_{0} (mh) - I_{0} (mr)} \right]} \right\} \\ & \quad + \frac{{G_{r} (1 - N)\left( {N_{b} - N_{t} } \right)}}{{2(2 - N)}} \\ & \quad \left\{ \begin{gathered} \frac{N}{{I_{1} \left( {mh} \right)}}\left( {\frac{{h^{5} }}{{96m}} - \frac{{h^{3} }}{{8m^{3} }} - {\text{~}}\frac{h}{{m^{5} }}} \right)\left[ {I_{0} (mh) - I_{0} (mr)} \right] \hfill \\ - \frac{{r^{6} }}{{576}} - \frac{{h^{6} }}{{72}} + \frac{{h^{4} r^{2} }}{{64}} - \frac{N}{{32m^{2} }}\left( {r^{4} - {\text{~}}h^{4} } \right) - \frac{{16N}}{{32m^{4} }}\left( {r^{2} - h^{2} } \right) \hfill \\ \end{gathered} \right\} \\ & \quad + \frac{{B_{r} (N - 1)}}{{2(2 - N)}}\frac{{N_{t} }}{{N_{b} }}\left\{ \begin{gathered} \frac{N}{{I_{1} \left( {mh} \right)}}\left( {\frac{{h^{3} }}{{8m}} - \frac{h}{{m^{3} }}} \right)\left[ {I_{0} (mh) - I_{0} (mr)} \right] \hfill \\ - \frac{1}{{16}}\left( {r^{4} + 3h^{4} } \right) - {\text{~}}\frac{N}{{2m^{2} }}\left( {r^{2} - h^{2} } \right) + \frac{{h^{2} r^{2} }}{4} \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

(16)

The dimension-less flux q is

$$ q = \int\limits_{0}^{h} {2ru_{z} \,dr} . $$

(17)

By substituting Eq. (16) in Eq. (17), the flux is

$$\begin{aligned} q & = \frac{{(1 - N)}}{{(2 - N)}}\frac{{dp}}{{dz}}\left\{ {\frac{{ - h^{4} }}{4} + \frac{{Nh^{3} I_{0} \left( {mh} \right)}}{{2mI_{1} \left( {mh} \right)}} - \frac{{Nh^{2} }}{{m^{2} }}} \right\} \\ & \quad + \frac{{B_{r} (N - 1)}}{{(2 - N)}}\frac{{N_{t} }}{{N_{b} }}\left\{ {\left( {\frac{{h^{5} }}{{16}} - \frac{{h^{3} }}{{2m^{2} }}} \right)\frac{{NI_{0} \left( {mh} \right)}}{{mI_{1} \left( {mh} \right)}} + \frac{{Nh^{2} }}{{m^{4} }} - \frac{{h^{6} }}{{24}}} \right\} \\ & \quad + \frac{{G_{r} (1 - N)\left( {N_{b} - N_{t} } \right)}}{{(2 - N)}}\left\{ \begin{gathered} \left( {\frac{{h^{7} }}{{192}} - \frac{{h^{5} }}{{16m^{2} }} - \frac{{h^{3} }}{{2m^{4} }}} \right)\frac{{NI_{0} (mh)}}{{mI_{1} (mh)}} \hfill \\ + \frac{{Nh^{4} }}{{4m^{4} }} + \frac{{Nh^{2} }}{{m^{6} }} - \frac{{5h^{8} }}{{1536}} \hfill \\ \end{gathered} \right\} \\ \end{aligned} $$

(18)

From Eq. (18), $\frac{dP}{dz}$ can be given as

$$ \begin{aligned} & \frac{{dp}}{{dz}} = \frac{{q(2 - N)}}{{S(N - 1)}} + \frac{{G_{r} \left( {N_{b} - N_{t} } \right)}}{S} \\ & \quad \left\{ {\left( {\frac{{h^{7} }}{{192}} - \frac{{h^{5} }}{{16m^{2} }} - \frac{{h^{3} }}{{2m^{4} }}} \right)\frac{{NI_{0} \left( {mh} \right)}}{{mI_{1} \left( {mh} \right)}} + \frac{{Nh^{4} }}{{4m^{4} }} + \frac{{Nh^{2} }}{{m^{6} }} - \frac{{5h^{8} }}{{1536}}} \right\} \\ & \quad - \frac{{B_{r} N_{t} }}{{SN_{b} }}\left\{ {\left( {\frac{{h^{5} }}{{16}} - \frac{{h^{3} }}{{2m^{2} }}} \right)\frac{{NI_{0} \left( {mh} \right)}}{{mI_{1} \left( {mh} \right)}} + \frac{{Nh^{2} }}{{m^{4} }} - \frac{{h^{6} }}{{24}}} \right\} \\ \end{aligned} $$

(19)

where $S = \left[ {\frac{{h^{4} }}{4} - \frac{{Nh^{3} I_{0} (mh)}}{{2mI_{1} (mh)}} + \frac{{Nh^{2} }}{{m^{2} }}} \right]$

The pressure drop over one wavelength $p(0) - p(\lambda )$ is

$$ \Delta p = - \int\limits_{0}^{1} {\frac{dp}{dz}dz} $$

(20)

The impedance $\lambda$ is defined as

$$ \lambda = \frac{{\Delta p}}{q} $$

(21)

The pressure drop without stenosis $h = 1$ is defined as

$$ \Delta p_{n} = \left[ { - \int\limits_{0}^{1} {\frac{dp}{dz} dz} } \right]_{h = 1} $$

(22)

The impedance in the normal artery is defined as

$$ \lambda_{n} = \frac{{\Delta p_{n} }}{q} $$

(23)

The normalized impedance defined as

$$ \bar{\lambda } = \frac{\lambda }{{\lambda_{n} }} $$

(24)

And the wall shear stress $\tau_{h}$ is defined as

$$ \tau_{h} = - \frac{h}{2}\frac{dp}{dz} $$

(25)

4 Result Analysis

Using MATHEMATICA 9.0 Software, computer codes are developed to evaluate analytical solutions for impedance $\left( {\bar{\lambda }} \right)$ and shear stress at wall $\left( {\tau_{h} } \right)$. The effects of pertinent parameters on impedance, shear stress at wall and nanoparticle phenomena have been computed numerically for different values of height of the stenosis and are presented graphically in Figs. 2, 3, 4, 5, 6, 7, 8, and 9 by considering the parameter values as $d = 0.2,\;{\text{L}}_{0} = 0.4,\;m = 1,\;q = 0.1,\;L = 1$, $N = 0.1,\;{\text{N}}_{\text{b}} = 0.3,\;{{N}}_{\text{t}} = 0.8,\;{{B}}_{\text{r}} = 0.3,\;{{G}}_{\text{r}} = 0.5$ [9, 10].

Fig. 2

Effect of $\delta$ and $N_{t} ,m$ on $\bar{\lambda }$

Fig. 3

Effect of $\delta$ and $N_{b} ,N$ on $\bar{\lambda }$

Fig. 4

Effect of $\delta$ and $G_{r} ,B_{r}$ on $\bar{\lambda }$

Fig. 5

Effect of $\delta$ and N, m on $\tau_{h}$

Fig. 6

Effect of $\delta$ and $N_{t} ,N_{b}$ on $\tau_{h}$

Fig. 7

Effect of $\delta$ and $G_{r} ,B_{r}$ on $\tau_{h}$

Fig. 8

Stream line patterns for different values of $N_{b}$

Fig. 9

Stream line patterns for different values of $N_{t}$

In Figs. 2, 3, and 4, it is observed that impedance $\left( {\bar{\lambda }} \right)$ increases with the heights of the stenosis (δ), micropolar parameter (m), thermophoresis parameter $(N_{t} )$, local temperature Grashof number $(G_{r} )$, and local nanoparticle Grashof number $(B_{r} )$ but decreases with coupling number (N) and Brownian motion parameter $(N_{b} )$.

The shear stress at wall $\left( {\tau_{h} } \right)$ acting over the height of the stenosis (δ) is shown graphically in Figs. 5, 6 and 7, it is seen that shear stress at wall increases with the heights of the stenosis (δ), coupling number (N) and Brownian motion parameter $(N_{b} )$ but decreases with micropolar parameter (m), thermophoresis parameter $(N_{t} )$, local temperature Grashof number $(G_{r} )$, and local nanoparticle Grashof number $(B_{r} )$.

Figures 8 and 9 illustrate the streamline patterns and it is noticed that size of bolus increases with the increase of Brownian motion parameter $(N_{b} )$ and size of the bolus decreases with the increase in thermophoresis parameter $(N_{t} )$.

5 Conclusion

A mathematical analysis for the steady flow of an incompressible micropolar fluid with nanoparticles in a tube having overlapping stenosis has been studied by assuming stenosis is to be mild. The analytical solutions of the governing equations are obtained by using Homotropy perturbation method. It is noticed that shear stress at wall increases with the stenotic heights, coupling number, and Brownian motion parameter but decreases with micropolar parameter, thermophoresis parameter, local temperature Grashof number and local nanoparticle Grashof number. Impedance increases with the heights of the stenosis, length of the stenosis, micropolar parameter, thermophoresis parameter, local temperature Grashof number, and local nanoparticle Grashof number but decreases with coupling number and Brownian motion parameter.