Keywords

1 Introduction

A new candidate element for brain-inspired computing has recently appeared: spintronics, which is the main topic of this chapter. In this section, we provide a brief introduction to this research field.

1.1 Recurrent Neural Network and Reservoir Computing

The brain has long been a fascinating research target in science. Nonlinear interactions between neurons in the brain via synapses carry and/or store information, and prompt the growth of living things. Human beings, as well as biological systems in general, show surprising computational ability due to their brains. The brain can perform various functions, including (visual and/or audio logic) recognition, associative memory, prediction from past experiences, action modification, and task optimization. Moreover, the human brain has notably low power consumption for computation. If we could replace current computing systems based on the von Neumann architecture by neural networks, our lives would be drastically changed. Brain-inspired computing aimed at achieving artificial neural networks has attracted much attention in a wide range of scientific research fields, such as physics, chemistry, biology, engineering, and nonlinear science.

A crucial task in the advancement of brain-inspired computing is developing an appropriate model (Gerstner et al. 2014; Goodfellow et al. 2017) and implementing it in a real system. A class of artificial neural network, called recurrent neural network (RNN), is an architecture exhibiting a dynamic response to a time sequence of an input data (Mandic and Chambers 2001). The response of an RNN depends not only on the input and the system’s weights at a certain time but also on the input at some previous time. In other words, RNNs store past input information. Thus, RNNs enable a time sequence of input data such as data on spoken languages and movies to be classified and calculated.

A reservoir computing system is an RNN in which the internal weights of the network are not changed by learning; only the reservoir-to-output weights are trained (Maass et al. 2002; Jaeger and Haas 2004; Verstraeten et al. 2007; Appeltant et al. 2011; Nakajima 2020). This approach simplifies the tuning of the weights used for computing and enables any physical system to be used as a “reservoir.” Various such systems have been developed, including a photonic architecture with delayed feedback (Brunner et al. 2013), a soft robotic reservoir using body dynamics generated from a soft silicone arm (inspired by octopus’s arm in water) (Nakajima et al. 2015), and a quantum reservoir consisting of several qubits (Fujii and Nakajima 2017).

The purpose of this chapter is to introduce a promising new candidate for reservoir computing: spintronics. Spintronics is a relatively young research field in condensed matter physics and has been developed by investigating spin-dependent electron transport in solids with nanometer (nm) scale. Spintronics technology has several advantages for reservoir computing, such as its applicability to an array structure with nanoscale dimensions, low energy consumption, and strong nonlinearity. However, the research targets in spintronics to date have been electronic devices, such as nonvolatile memory and microwave generators, and the ability of spintronics technology from the viewpoint of artificial neural networks has not yet been thoroughly investigated. What is required in reservoir computing is rich (or complex) dynamics of physical systems because the reservoir should show several and distinguishable responses to different sequences and/or inputs. The richness (or complexity) of a dynamical system is quantitatively characterized by its memory and nonlinear capacities, which characterize, respectively, the amount of information the RNN can store and its nonlinear computational capability. Here, the capacities are estimated by examining the response to binary input as done in Jaeger (2002). Short-term memory capacity is simply characterized how much past information fed into the system can be stored and reconstructed from the current output of the reservoir with trained weight. This task can be accomplished even in a linear system, in principle. Therefore, the nonlinear computational capability on the stored information is further characterized by the parity check capacity by predicting the parity of the past input sequence, which essentially requires nonlinearity. For example, the short-term memory capacity of a quantum reservoir consisting of several qubits (\({\ge }4\)) with virtual nodes (\({\ge }4\)) was reported to be of the order of 10 (Fujii and Nakajima 2017). In this chapter, we describe our recent measurements of memory capacity in spintronics devices (Tsunegi et al. 2018a; Furuta et al. 2018).

We start by describing the history of this research field, and discuss the applicability of spintronics technology to brain-inspired computing.

1.2 History of Spintronics and Key Technologies

An electron has two degrees of freedom, charge and spin. Research on electricity and magnetics has a long history, and it was unified at the end of the nineteenth century as classical electromagnetism (Jackson 1999). People began to notice that both electricity and magnetism originate from a charged particle, but it took time to widely accept the existence of elementary particles (or atoms and molecules) until the beginning of the twentieth century. The rapid growth of quantum mechanics provided a new picture of electrons and of elementary particles, in general, which resulted in a drastic change in our understanding of the nature. In particular, the discovery of spin led the transition from classical to quantum physics because it was the first finding of an internal degree of freedom in elementary particles (Dirac 1928). Spin has relativistic quantum mechanical origin (Weinberg 2005), determines the statistics of the elementary particles (Pauli 1940), and is related to many physics, such as the stimulated emission of light (Dirac 1927), the origin of ferromagnetism (Heisenberg 1928), superconductivity (Bardeen et al. 1957), and the fate of stars (Chandrasekhar 1984). Importantly, the quantum mechanics has also resulted in the development of applied physics. Electronics based on semiconductors has provided many devices useful in everyday life. Magnetic devices as well have become widely used for such things as a storage device. Charge and spin have been, however, used separately for electronics and magnetic devices, respectively.

Spintronics (or spin electronics) is both electronics and magnetism at nanoscale and aims to develop new electronics devices, such as nonvolatile memory [magnetoresistive random access memory (MRAM)] and microwave generators, in which spin plays a key role. Quantum mechanical interactions between the spins of conducting electrons in metals and semiconductors, magnetization in ferromagnets, magnons (spin-wave quanta) in insulating ferromagnets, light helicity, and so on provide interesting new phenomena in fundamental physics and have opened the door to practical applications. The growth of spintronics is due to advances in nanostructure fabrication processes. This is because the spin of electrons in condensed matter is not a conserved quantity. For example, the spin in metals relaxes over the length scale (the spin diffusion length) (Valet and Fert 1993), which is typically of the order of nanometers (Bass and Pratt 2007); therefore, nanostructures are necessary to observe spin-dependent phenomena.

A key phenomenon in spintronics is the tunneling magnetoresistance (TMR) effect, which was found by Julliere in a magnetic tunnel junction (MTJ) consisting of Fe/Ge/Co (Julliere 1975). The magnetoresistance effect is a physical phenomenon in which the resistance of an electrical circuit depends on the magnetization directions of the ferromagnets. The TMR effect originates from spin-dependent tunneling through an insulator, and so it is a purely quantum mechanical phenomenon. Although several other magnetoresistance effects, such as anisotropic magnetoresistance and the planar Hall effect, have been found since the nineteenth century and their origins were revealed to be quantum mechanical phenomena in the middle of the twentieth century (Thomson 1856; Kundt 1893; Pugh and Rostoker 1953; Karplus and Luttinger 1954; McGuire and Potter 1975; Sinitsyn 2008; Nagaosa et al. 2010), the discovery of the TMR effect in 1975 is often regarded as a beginning of spintronics. Since the electrons pass through the interfaces between multilayers, the structure of an MTJ is often called a “current-perpendicular-to-plane (CPP)” structure. The research target shifted from MTJs (Julliere 1975; Maekawa and Gäfvert 1982; Maekawa and Shinjo 2002) to giant magnetoresistive (GMR) systems consisting of metallic ferromagnetic/nonmagnetic multilayers when the relatively large magnetoresistance effect, called the “GMR effect,” was found in 1988–1989 by Fert and Grünberg independently (Baibich et al. 1988; Binasch et al. 1989). The GMR effect was first observed in a current-in-plane (CIP) structure, in which the electrons move in a direction parallel to the metallic interface. It was, however, soon noticed that the CPP structure shows a larger GMR effect than the CIP structure (Pratt et al. 1991; Zhang and Levy 1991). Research interest shifted to back MTJs when a large TMR effect was found in an Fe/AlO/Fe MTJ in 1995 (Miyazaki et al. 1995; Moodera et al. 1995) and a giant TMR effect was found in an MTJ with an Fe/MgO/Fe MTJ in 2004 (Yuasa et al. 2004a; Parkin et al. 2004; Yuasa et al. 2004b).

A magnetoresistance effect, such as the TMR effect, enables the magnetization direction in a ferromagnet to be detected by using an electrical circuit. Typical TMR and GMR devices include two ferromagnets, and the resistance of the circuit is low (high) when the alignment of their magnetizations is parallel (antiparallel). In addition, the theoretical prediction of a spin-transfer torque (STT) effect by Slonczewski and Berger provided a new technology controlling the magnetization direction (Slonczewski 1989, 1996; Berger 1996; Slonczewski 2005). After the discovery of magnetism, the magnetization direction of a ferromagnet has been controlled by applying an external magnetic field. The STT effect is a completely different phenomenon, where an electric current is applied to a ferromagnetic/nonmagnetic/ferromagnetic trilayer structure. One ferromagnet, the “reference layer,” acts as a polarizer of the spin angular momentums of the conducting electrons. When these spin-polarized electrons are injected into the other ferromagnet, the “free layer,” the spins of the conducting electrons are transferred to the magnetization of the ferromagnet via quantum mechanical interaction and excite STT (Ralph and Stiles 2008). When the magnitude of the electric current is sufficiently large, the STT can change the magnetization direction in the free layer. Such magnetization reversals were observed in a GMR device in 2000 (Katine et al. 2000) and in an MTJ in 2005 (Kubota et al. 2005).

In summary, there are two important phenomena in spintronics, the TMR and STT effects. The magnetization direction of a nanostructured ferromagnet can be detected electrically by using the TMR effect and can be changed by using the STT effect. These are the operation principles for any kind of spintronics device (Locatelli et al. 2014). In fact, as discussed below, brain-inspired computing based on spintronics technology utilizes these phenomena. There are many other interesting phenomena in spintronics, such as the spin pumping effect (Silsbee et al. 1979; Tserkovnyak et al. 2002; Mizukami et al. 2002), the spin Hall effect (Dyakonov and Perel 1971; Hirsch 1999; Kato et al. 2004), and the topological effect (Murakami et al. 2003). Readers who are interested in spintronics can easily find good textbooks and review articles, such as Maekawa (2006), Shinjo (2009), and Maekawa et al. (2012).

1.3 Brain-Inspired Computing Based on Spintronics

There are many advantages of applying spintronics technology to brain-inspired computing (Grollier et al. 2016). First of all, the small size of spintronics device and their applicability to an array structure enable development of high-density computing devices. The typical size of an MTJ is of the order of 1 nm in thickness and 10–100 nm in diameter (Fukushima et al. 2018; Watanabe et al. 2018). The nonvolatility of the magnetization as memory results in low power consumption during operation (Dieny et al. 2016). The large output signal due to the giant TMR effect is another advantage for electronics applications (Yuasa et al. 2004a; Parkin et al. 2004; Yuasa et al. 2004b; Djayaprawira et al. 2005; Ikeda et al. 2008; Yakushiji et al. 2010; Sukegawa et al. 2013; Kubota et al. 2013; Tsunegi et al. 2016a). The figure of merit for TMR and GMR devices is the magnetoresistance ratio, which is defined as \((R_\mathrm{AP}-R_\mathrm{P})/R_\mathrm{P}\), where \(R_\mathrm{P}\) and \(R_\mathrm{AP}\) are the resistances of the system for parallel (P) and antiparallel (AP) magnetization alignments. Currently, the TMR ratio is of the order of 100%, which results in a visible change in the output signal that is sufficient to experimentally detect by overcoming noise. Strong nonlinearity of the magnetization dynamics excited by the STT effect (Bertotti et al. 2005, 2007, 2009; Slavin and Tiberkevich 2009) is desirable for computation calculating a time sequence of input data. In fact, as mentioned below, we found that an MTJ with TMR and STT effects is applicable as an element for reservoir computing. The fast relaxation time of the magnetization dynamics (Zhou et al. 2010; Kudo et al. 2010; Suto et al. 2011; Nagasawa et al. 2011; Rippard et al. 2013; Jenkins et al. 2016; Taniguchi et al. 2017; Tsunegi et al. 2018b), of the order of 1–100 nanoseconds (ns), is suitable for fast computing. Application of these features to brain-inspired computing by using spintronics technology has recently been reported.

An associative memory operation in a network consisting of CIP devices was reported by Borders, Fukami, and their collaborators in 2017 (Borders et al. 2017). They used analog switching of the magnetization in a CoNi ferromagnet placed on a PtMn antiferromagnet as memory for storing the weight of computing. A total of 36 devices were used to demonstrate the associative memory operation of identifying a word consisting of three alphabetic letters.

Spoken-digit recognition competitive to that of state-of-the-art neural networks was demonstrated by Torrejon, Grollier, and their collaborators, including some of the present authors of this chapter, also in 2017 (Torrejon et al. 2017). A vortex spin-torque oscillator (STO) was used for the computation, and the information of a sequence of spoken words was stored using the nonlinear dynamics of the magnetic vortex. A high recognition rate (\({\ge }95\)%) was obtained for spoken digits (0–9) pronounced by five speakers. The detail of this work is explained in the other chapter of this book. Vowel recognition with four coupled STOs was also achieved recently (Romera et al. 2018). In the following sections, we will revisit artificial neural networks based on an STO.

There have also been several reports of numerical simulation focused on brain-inspired computing based on a spintronics computing architecture (Furuta et al. 2018; Vodenicarevic et al. 2017; Kudo and Morie 2017; Huang et al. 2017; Nakane et al. 2018; Chen et al. 2018; Pinna et al. 2018; Arai and Imamura 2018; Nomura et al. 2018). For example, Kudo and Morie demonstrated pattern recognition using an array of STOs in 2017 (Kudo and Morie 2017). Nakane and his collaborators investigated the possibility of reservoir computing based on spin-wave excitation and detection in 2018 (Nakane et al. 2018). As can be seen, a wide variety of device designs have been proposed. This is due to the rich physics of nanostructured devices. The magnetization dynamics in a ferromagnet is usually highly nonlinear. Since spintronics devices consist of nanomagnets, magnetic interactions, such as dipole interaction and spin wave, can be used as an operation principle. In addition, electrical interaction through the STT effect can also be an operation principle for such devices. Accordingly, spintronics provides interesting examples of dynamical systems and therefore can be considered a strong candidate as a fundamental element of brain-inspired computing, see, for example, a review (Grollier et al. 2020) including both experiments and theory.

1.4 Spin-Torque Oscillator (STO)

A key device for brain-inspired computing based on spintronics technology is the STO (Torrejon et al. 2017). An STO typically consists of an MTJ, for which the main structure is a trilayer (reference layer/insulating barrier/free layer), as illustrated in Fig. 1a. The typical material for the barrier is MgO (Yuasa et al. 2004a, b; Parkin et al. 2004). As mentioned above, when an electric current is injected into an MTJ, STT is excited on the magnetization in the free layer. The STT leads to magnetization dynamics when the magnitude of the electric current is sufficiently large. The magnetization dynamics is typically classified as reversal (Kubota et al. 2005) or oscillation (Kiselev et al. 2003). Magnetization reversal has been used as an operation principle for MRAM (Dieny et al. 2016). Magnetization oscillation has been widely studied for both GMR and TMR structures with the aim of developing practical applications such as microwave generator, highly sensitive sensors, and phased array radar (Kiselev et al. 2003; Rippard et al. 2004; Houssameddine et al. 2007). An STO device uses this magnetization oscillation in an MTJ for such practical applications.

Fig. 1
figure 1

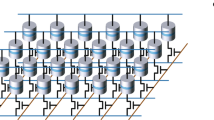
a Schematic diagram of fundamental structure of MTJ connected to electric battery. b Schematic diagram of MTJ with vortex-type free layer. Each white arrow represents local direction of magnetic moment \(\mathbf {m}(\mathbf {x})\). Magnetic moment at center points in the perpendicular direction with respect to film surface and is called a “vortex core.” Magnetic moments around core lie in film plane. c Schematic diagram of MTJ with macromagnetic free layer. Almost all local magnetic moments point in same direction, so local variable \(\mathbf {m}(\mathbf {x})\) can be replaced with macroscopic variable \(\mathbf {m}\). In both b, c, direction of magnetization in reference layer, which is assumed to be macromagnetic, is represented as \(\mathbf {p}\)

Full size image

Since STOs are nonlinear oscillator showing an auto-oscillation (a limit cycle), there are a dissipation due to friction and source of energy injection, as is any auto-oscillator in nature (Pikovsky et al. 2003). The source of the energy is the work done by the STT, while the dissipation is relaxation minimizing the magnetic energy of the ferromagnets. The oscillation frequency ranges from 100 MHz to 100 GHz depending on the device structure and magnetic configuration, see Sects. 2.1, 2.2, and 2.3 for more detail. The oscillation of the magnetization in an STO is detected through the TMR effect. The resistance of the MTJ is \(R=1/G\), where conductance G is given by

$$\begin{aligned} G = \frac{G_\mathrm{P}+G_\mathrm{AP}}{2} + \frac{G_\mathrm{P}-G_\mathrm{AP}}{2} \cos \theta , \end{aligned}$$
(1)

where \(\theta \) is the relative angle between the magnetizations of the free and reference layers, and \(G_\mathrm{P}=1/R_\mathrm{P}\) and \(G_\mathrm{AP}=1/R_\mathrm{AP}\) are the conductances for the parallel and antiparallel magnetization alignments. Therefore, the resistance, or voltage, of the STO oscillates over time when the magnetization in the free layer is in an auto-oscillation state. In other words, the oscillation state of the STO can be detected by electrical measurement.

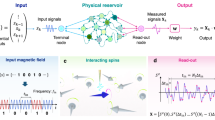
Our motivation focusing on reservoir computing based on spintronics technology is as follows. Imagine that we fabricate an array of STOs. Each STO interacts with the other STOs through magnetic and/or electrical interactions. Such a system may experience phase synchronization (Slavin and Tiberkevich 2009), in which the phase differences between the magnetizations saturate to certain values. This synchronization phenomenon may be applicable to some portion of brain-inspired computing (Kudo and Morie 2017). It should be noted, however, that the coupling strength between the STOs normally cannot be changed after fabrication of the array. This means that the interconnections (weights) between the elements in the RNN cannot be tuned for computing. Reservoir computing solves this problem and thus opens the door to the applicability of STO devices to brain-inspired computing. The highly nonlinear, and thus complex, dynamics of STOs should provide rich dynamics to a reservoir and is unnecessary to be tuned for computing. To clarify the applicability of STO devices to reservoir computing it is necessary to evaluate the performance capabilities of STOs, which is the main objective of this chapter (Tsunegi et al. 2018a; Furuta et al. 2018).

2 Methods

In this section, we summarize the methods we used to evaluate the short-term memory and parity check capacities of reservoir computing with STOs.

2.1 Landau–Lifshitz–Gilbert Equation

We start by introducing a theoretical model of the magnetization dynamics frequently used in the fields of magnetism and spintronics. It is often assumed that the magnetization dynamics in a ferromagnet is described by the Landau–Lifshitz–Gilbert (LLG) equation with spin-transfer torque (Slonczewski 1996; Landau and Lifshitz 1935):

$$\begin{aligned} \frac{\mathrm{d}\mathbf {m}}{\mathrm{d}t} = -\gamma \mathbf {m} \times \mathbf {H} - \frac{\gamma \hbar P g(\theta )J}{2eM_\mathrm{s}d} \mathbf {m} \times \left( \mathbf {p} \times \mathbf {m} \right) + \alpha \mathbf {m} \times \frac{\mathrm{d}\mathbf {m}}{\mathrm{d}t}, \end{aligned}$$
(2)

where \(\mathbf {m}\) is the unit vector pointing in the local magnetization direction. Magnetic field \(\mathbf {H}\) consists of both internal and external fields; the internal fields include an exchange field, anisotropy field, and dipole field. Parameter \(\gamma \), the “gyromagnetic ratio,” is related to Bohr magneton \(\mu _\mathrm{B}\) and Landé g-factor \(g_\mathrm{L}\) via \(\gamma =g_\mathrm{L}\mu _\mathrm{B}/\hbar \). Saturation magnetization \(M_\mathrm{s}\) is the magnetic moment per volume, whereas d is the thickness of the free layer. Spin polarization P (\(0\le P <1\)) characterizes the strength of the STT, and the vector \(\mathbf {p}\) (\(|\mathbf {p}|=1\)), which is usually parallel to the magnetization of the reference layer, determines the direction of the STT. The current density flowing in the MTJ is denoted as J. Factor \(g(\theta )\), a function of the relative angle between \(\mathbf {m}\) and \(\mathbf {p}\) (\(\cos \theta =\mathbf {m}\cdot \mathbf {p})\), determines the angular dependence of the STT. The explicit form of \(g(\theta )\) depends on the structure of the spintronics device (Xiao et al. 2004; Taniguchi et al. 2015). Dimensionless parameter \(\alpha \), the “damping constant,” which characterizes the strength of the dissipation due to friction of the magnetization dynamics (Gilbert 2004) and is of the order of \(10^{-3}-10^{-2}\) for typical ferromagnets used in spintronics devices (Oogane et al. 2006). The magnetization dynamics in a ferromagnet has been investigated by solving the LLG equation both analytically (Bertotti et al. 2009) and numerically (Lee et al. 2004).

The LLG equation is a nonlinear differential equation. The first term on the right-hand side of Eq. (2) is the field-torque term and describes a steady precession (oscillation) of the magnetization around the magnetic field. The second (STT) term moves the magnetization parallel or antiparallel to the direction of \(\mathbf {p}\) depending on the direction of the electric current. The third term (the damping term) describes the energy dissipation of the ferromagnet phenomenologically (Gilbert 2004). Auto-oscillation of magnetization \(\mathbf {m}\) in an STO is excited when the energy dissipation (\(\propto \alpha \)) is cancelled by the energy supplied by the work done by the STT (Bertotti et al. 2009). When this condition is satisfied, the auto-oscillation around the magnetic field, which is described by the field-torque term, is realized. The oscillation trajectory is almost on a constant energy curve (Bertotti et al. 2009).

2.2 Micro- and Macro-Structures of Nanomagnet

For the following discussions, we need to briefly review the microstructure of the free layer. As mentioned above and shown in Fig. 1a, the size of the free layer is typically 10–100 nm in diameter and 1 nm in thickness. Such a ferromagnet consists of numerous magnetic atoms, so its macroscopic magnetization consists of numerous magnetic moments. The direction of each magnetic moment in equilibrium is determined to minimize the magnetic energy E, which is related to the magnetic field \(\mathbf {H}\) via \(\mathbf {H}=-\delta E/\delta (M \mathbf {m})\) (Lifshitz and Pitaevskii 1980), and consists of the exchange energy, magnetic anisotropy energy, dipole field energy, and Zeeman energy (Hubert and Schäfer 1998).

When the free layer, in particular the thickness, is relatively large, the microstructure of each magnetic moment becomes a vortex so as to minimize the stray field energy, i.e., the magnetic moment at the center of the area points in the direction perpendicular to the cross-sectional area of the free layer whereas the magnetic moments around the center exhibit a chiral structure, as illustrated in Fig. 1b. In this case, \(\mathbf {m}\) is a function of location \(\mathbf {x}\) inside the free layer. Another micromagnetic structure called domain wall separates two uniformly magnetized domains. One way to investigate the magnetization dynamics in such systems is to use the LLG equations to compute the magnetization dynamics of all the magnetic moments simultaneously, i.e., by using numerical micromagnetic simulation (Brown and LaBonte 1965; Hayashi and Goto 1971; Nakatani et al. 1989, 2003; Dussaux et al. 2010). Another way to investigate the dynamics is to reduce the LLG equation to an equation of motion of the vortex core. The reduced equation is called Thiele equation, which describes the motions of the radius and rotation angle in the film plane of the vortex core (Thiele 1973; Guslienko 2006; Liu et al. 2007; Khvalkovskiy et al. 2009; Dussaux et al. 2012; Grimaldi et al. 2014).

On the other hand, when the free layer is relatively small, almost all magnetic moments point in the same direction so as to minimize the exchange and anisotropy energies. In this case, we can replace local magnetization \(\mathbf {m}\) in Eq. (2) with a macroscopic single moment as illustrated in Fig. 1c. This model is called a macromagnetic or macrospin model. The macromagnetic magnetization in the thin magnetic film used in spintronics devices usually points in the direction parallel to the film plane. This is because this in-plane magnetized configuration minimizes the stray field generated outside the ferromagnet and reduces the magnetic energy. The magnetization can be, however, oriented in the direction perpendicular to the film plane by controlling the perpendicular anisotropy energy. For example, adding an MgO barrier neighboring a CoFe ferromagnet induces an interface anisotropy effect (Hine et al. 1979; Yakata et al. 2009; Ikeda et al. 2010; Kubota et al. 2012). Applying an electrical voltage also changes the perpendicular anisotropy due to interface effect (Weisheit et al. 2007; Chiba et al. 2008; Maruyama et al. 2009; Nozaki et al. 2010; Shiota et al. 2012). The perpendicularly magnetized MTJ is of great interest for MRAM applications because it is suitable for high-density structures.

The number of variables in Eq. (2) for the vortex structure is \(2\mathcal {N}\), where \(\mathcal {N}\) is the number of magnetic moments. In the macromagnetic case, the number of variables is 2. One might consider that, since vector \(\mathbf {m}\) is defined in a three-dimensional space, the number of variables should be \(3\mathcal {N}\) and 3 for the vortex and macromagnetic case. However, the LLG equation conserves the norm of magnetization \(\mathbf {m}\) because the equation satisfies \(\mathrm{d}|\mathbf {m}|^{2}/\mathrm{d}t=(1/2)\mathbf {m}\cdot (\mathrm{d}\mathbf {m}/\mathrm{d}t)=0\), so there is a constraint condition \(|\mathbf {m}|=1\), which reduces the number of independent variables. This conservation of the magnetization norm means that the temperature of the system is sufficiently lower than the Curie temperature of the ferromagnet. According to the Poincaré–Bendixson theorem (Wiggins 1990), chaos is precluded in a macromagnetic model without interaction with other ferromagnets and/or feedback. Magnetization \(\mathbf {p}\) in the reference layer is usually assumed to be macromagnetic.

The ferromagnets used in spintronics devices typically have two energy minima due to uniaxial anisotropy energy. Such a ferromagnet can be used as a bit of memory devices. The strengths of the STT and damping torque represented in Eq. (2) depend on the direction of the magnetization. Related to this fact, there are two thresholds, \(J_\mathrm{c}\) and \(J_\mathrm{sw}\), of current density J in Eq. (2). When \(J/J_\mathrm{c}>1\), the STT exceeds the damping torque near the equilibrium state and destabilizes the magnetization. When \(J/J_\mathrm{sw}>1\), the magnetization moves from one equilibrium to another. Note that auto-oscillation of the magnetization is excited in range \(J/J_\mathrm{c}>1\) and \(J/J_\mathrm{sw}<1\). To satisfy these conditions, \(J_\mathrm{sw}/J_\mathrm{c}\) should be larger than one. If this condition is not satisfied, i.e., \(J_\mathrm{sw}/J_\mathrm{c}<1\), the MTJ exhibits the switching without showing an auto-oscillation (Taniguchi et al. 2013; Taniguchi 2015). This means that not all MTJs exhibit an auto-oscillation. The magnitude relationship between \(J_\mathrm{c}\) and \(J_\mathrm{sw}\) depends on the magnetic field and STT angular dependence.

The oscillation frequencies of a vortex and macromagnetic STO are typically of the order of 100 MHz and 1–10 GHz, respectively. A vortex-type STO was used for the experimental estimation of short-term memory capacity (Sect. 3) whereas the macromagnetic model was used for the numerical simulation (Sect. 4).

2.3 Recurrent Neural Network Based on STO

We developed two models of an STO-based RNN. One uses a single vortex-type STO, while the other uses a single macromagnetic STO or nine macromagnetic STOs as a reservoir. In both models, the output voltage from the STO is used as the dynamic response from the reservoir. According to Eq. (1), the resistance, or voltage, of an STO oscillates due to the oscillation of magnetization \(\mathbf {m}\) in the free layer (\(\cos \theta =\mathbf {m}\cdot \mathbf {p}\)). The output voltage from the STO is given by

$$\begin{aligned} v_\mathrm{out}(t) = v_\mathrm{a}(t) \sin \left[ 2\pi ft + \varphi _\mathrm{out}(t) \right] , \end{aligned}$$
(3)

where f is the oscillation frequency of the TMR. Amplitude \(v_\mathrm{a}\) and phase \(\varphi _\mathrm{out}\) of the voltage are constant in an auto-oscillation state. On the other hand, when an additional current (voltage) pulse is applied to the STO, they vary over time. This is because the additional torque changes the balance between the STT and damping torque, causing the magnetization to move a different oscillation state. The relaxation process for the new oscillation state depends on the sequence of additional voltage pulses. In other words, the STO in the relaxation process stores past input information. Therefore, the STO is a candidate for reservoir computing. The ability of a reservoir is quantitatively characterized by its memory and nonlinear capacities, as mentioned in Sect. 1.1. Therefore, it is necessary to evaluate the memory and nonlinear capacities of STO devices.

2.4 Methods for Evaluating Memory Capacities

Here, we describe methods for evaluating the short-term memory and parity check capacities.

We first explain, with the help of Fig. 2, how we evaluate short-term memory capacity. The figure schematically shows how the input is applied to the STO and how the output is obtained. As mentioned, memory capacity is evaluated by examining the response to binary input. We first sequentially apply Z-bit random voltage pulses (Z: integer) to the STO. The input voltage is expressed as \(V_{\mathrm{in},k}=V_\mathrm{low}+(V_\mathrm{high}-V_\mathrm{low})s_{\mathrm{in},k}\), where \(V_\mathrm{low}\) and \(V_\mathrm{high}\) are the lower and higher values of the input voltages, respectively, whereas \(s_{\mathrm{in},k}=0\) or 1 is the random binary data. The memory capacity is evaluated by examining the response of the reservoir to binary input (Jaeger 2002), and therefore masking procedure (Appeltant et al. 2011) is not applied to the input data in this work. The total length of the voltage pulses is \(Z \Delta t\), where \(\Delta t\) corresponds to the duration of 1 bit. These input data are called training data. The kth (\(k=1,2,\ldots ,Z\)) pulse is applied from time \(t=(k-1)\Delta t\) to \(t=k \Delta t\).

Fig. 2
figure 2

Schematic illustration of input voltage \(V_\mathrm{in}\) and output signal X(t). The numbers such as k and \(k+1\) indicate the pulse numbers. The kth input voltage is \(V_{\mathrm{in},k}=V_\mathrm{low}+(V_\mathrm{high}-V_\mathrm{low})s_{\mathrm{in},k}\); the corresponding output signal at the ith node is \(X_{k,i}\), where \(s_{\mathrm{in},k}\) is input binary data. For evaluation of short-term memory capacity, training data \(y_{\mathrm{STM},k}\) was directly related to input data via \(y_{\mathrm{STM},k}=s_{\mathrm{in},k}\). Weight \(w_{D,i}\) was determined so as to reproduce \(y_{\mathrm{STM},k}\) (\(V_{\mathrm{in},k-D}\)) from \(X_{k,i}\). Cases \(D=0\) and \(D=1\) are shown in figure. For evaluation of the parity check capacity, training data \(y_{\mathrm{PC},k}\) was related to input binary data (voltage) via Eq. (12) (After Tsunegi et al. 2018a)

Full size image

The STT excited by the input voltage changes the oscillation trajectory of the magnetization, resulting in a change in the voltage output from the STO, as schematically shown in Fig. 2. Not only the output voltage but also the STO variables can be used for the evaluation. For example, in Sect. 3, voltage amplitude \(v_\mathrm{a}\) is used as the output signal, whereas resistance x is used in the simulation described in Sect. 4. In this section, we denote a general signal output from an STO as X(t). We divide the output signal from \(t=(k-1)\Delta t\) to \(t=k\Delta t\) into N-nodes, where N is the number of virtual nodes. These virtual nodes are used, along with linear regression, to obtain the output from the reservoir. For simplicity, we denote the output signal at the ith (\(i=1,2,\ldots ,N\)) node as \(X_{k,i}\), i.e.,

$$\begin{aligned} X_{k,i} = X \left( (k-1) \Delta t + i \frac{\Delta t}{n} \right) . \end{aligned}$$
(4)

Weight \(w_{0,i}\) is then introduced to obtain the output from the reservoir;

$$\begin{aligned} \sum _{i=1}^{N+1} w_{0,i} X_{k,i}. \end{aligned}$$
(5)

The learning task here is to find the weight that minimizes the error between the output from the reservoir and the training data, which is defined as

$$\begin{aligned} \sum _{k=1}^{Z} \left( \sum _{i=1}^{N+1} w_{0,i} X_{k,i} - y_{\mathrm{STM},k} \right) ^{2}, \end{aligned}$$
(6)

where \(y_{\mathrm{STM},k}\) is the training data used for evaluating short-term memory capacity, and is related, specifically for the case without any delay, to the input binary data \(s_{\mathrm{in},k}\);

$$\begin{aligned} y_{\mathrm{STM},k} = s_{\mathrm{in},k}. \end{aligned}$$
(7)

The meaning of the suffix “0” in \(w_{0,i}\) in Eq. (6) will be explained below. The term with subscript \(i=N+1\) corresponds to the bias term used to tune the constant value, and \(X_{k,N+1}=1\) in Eq. (6).

Weight \(w_{0,i}\) introduced above is determined to reproduce training data \(y_{\mathrm{STM},k}\) applied during time \((k-1)\Delta t \le t \le k \Delta t\). Since an RNN is an artificial neural network used for classifying and calculating a time sequence of input data, it should be able to reproduce the past input voltage from the current output signal. To enable this functionality, Eq. (6) is extended:

$$\begin{aligned} \sum _{k=1}^{Z} \left( \sum _{i=1}^{N+1} w_{D,i} X_{k,i} - y_{\mathrm{STM},k-D} \right) ^{2}, \end{aligned}$$
(8)

where \(D=1,2,3,..\) is the delay. Weight \(w_{D,i}\) is set so as to reproduce the \((k-D)\)th input binary data \(y_{\mathrm{STM},k-D}\) applied during time \((k-D-1)\Delta t \le t \le (k-D) \Delta t\) from output signal X(t) obtained during time \((k-1)\Delta t \le t \le k \Delta t\).

After this learning, other \(Z^{\prime }\)-random pulse sequences \(s_{\mathrm{in},n}^{\prime }\) are applied to the STO as voltages, where \(Z^{\prime }\) is the number of input data instances. The prime symbol is used to distinguish the quantities related to testing from those related to learning. Test data \(y_{\mathrm{STM},n}^{\prime }\) is defined similarly to Eq. (7), i.e., \(y_{\mathrm{STM},n}^{\prime }=s_{\mathrm{in},n}^{\prime }\). The output signal at the ith node responsive to the nth test data is denoted as \(X_{n,i}^{\prime }\). Using the weight determined by the learning, we define the reconstructed data as

$$\begin{aligned} y_{\mathrm{R},n-D}^{\prime } = \sum _{i=1}^{N+1} w_{D,i} X_{n,i}^{\prime }, \end{aligned}$$
(9)

where \(X_{n,N+1}=1\). Whether the reconstructed data reproduces the test data with delay D is characterized by correlation coefficient \(\mathrm{Cor}(D)\) given by

$$\begin{aligned} {\begin{matrix}&\mathrm{Cor}(D) = \frac{\sum _{n=1}^{Z^{\prime }} \left( y_{\mathrm{STM},n-D}^{\prime }- \langle y_{\mathrm{STM},n-D}^{\prime } \rangle \right) \left( y_{\mathrm{R},n-D}^{\prime } - \langle y_{\mathrm{R},n-D}^{\prime } \rangle \right) }{\sqrt{ \sum _{n=1}^{Z^{\prime }} \left( y_{\mathrm{STM},n-D}^{\prime }- \langle y_{\mathrm{STM},n-D}^{\prime } \rangle \right) ^{2} \sum _{n=1}^{Z^{\prime }} \left( y_{\mathrm{R},n-D}^{\prime } - \langle y_{\mathrm{R},n-D}^{\prime } \rangle \right) ^{2} }}, \end{matrix}} \end{aligned}$$
(10)

where \(\langle \cdots \rangle \) is the average value. The short-term memory capacity is estimated as

$$\begin{aligned} C_\mathrm{STM} = \sum _{D=1}^{Z^{\prime }} [\mathrm{Cor}(D)]^{2}. \end{aligned}$$
(11)

The short-term memory capacity characterizes the ability of the reservoir to store past input as is, which can be done by simply using a linear transformation. The nonlinear transformation ability for the stored information can be examined by using a parity check task, where the following task data are used for the learning and testing:

$$\begin{aligned} y_{\mathrm{PC}, k-D} = \sum _{i=0}^{D} s_{\mathrm{in},k-D+i}\ \ \ \ \mathrm{mod}\ 2. \end{aligned}$$
(12)

The ability of the nonlinear transformation is quantitatively evaluated by introducing parity check capacity \(C_\mathrm{PC}\), which is defined similarly to Eq. (11). In the evaluation of parity check capacity, the data input to the STO is again binary voltage data. However, when the weight is determined, \(y_{\mathrm{PC},k-D}\) given by Eq. (12) should be substituted into the right-hand side of Eqs. (6) and (8). Similarly, during testing, test data \(y_{\mathrm{PC},n}^{\prime }\) are defined from the input binary data in accordance with Eq. (12) whereas the reconstructed data \(y_\mathrm{R}^{\prime }\) are obtained from the signal output from the STO and the weight determined by the learning, as shown in Eq. (9). The parity check capacity \(C_\mathrm{PC}\) is evaluated from the correlation between the test and reconstructed data.

3 Reservoir Computing with STO (Experiment)

In this section, we report our experimental evaluation of the short-term memory capacity of a vortex-type STO.

3.1 Experimental Methods

The STO used in this study was made from an MTJ with a multilayer structure: sub/buffer/PtMn(15)/CoFe(2.5)/Ru(0.86)/CoFeB(1.6)/CoFe(0.8)/MgO(1.1)/CoFe(0.5)/ FeB(7.0)/CoFe(0.5)/ MgO(1.0)/Ta/Ru (thickness in nm). The films were patterned into an STO with a diameter of 425 nm. The CoFe/Ru/CoFeB/CoFe and CoFe/FeB/CoFe structures correspond to the free and reference layers, respectively. A magnetic vortex state, as schematically shown in Fig. 1b, appears in the free layer in this type of MTJ (Tsunegi et al. 2016a, 2018b).

Figure 3a schematically shows the circuit used for evaluating the short-term memory capacity of the STO. We first prepared random binary bits as input data. The data were converted into voltage pulses by using an arbitrary wave generator (AWG). Voltage pulses with duration \(\Delta t\) and a 5 ns lead edge were applied to the STO through a low-pass filter using a bias-tee with a cutoff frequency of 300 MHz. We used filters corresponding to a Gaussian filter and applied the inverse of the circuit transfer function to the input voltage to reduce the distortion in preprocessing. The waveform of the high-frequency output voltage was measured at room temperature using a real-time oscilloscope (5–10 Gsam/s) using a high-pass filter with a cutoff frequency of 400 MHz. The STO generated an oscillating voltage through auto-oscillation of the vortex core induced by the perpendicular component (film normal) of the STT (Dussaux et al. 2010). Therefore, we applied an out-of-plane magnetic field of 725 mT to the oscillator. The voltage output from the STO was separated from the input voltage by using the high-pass filter and measured with the oscilloscope. Amplitude \(v_\mathrm{a}\) of the output voltage was estimated by using Hilbert transformation and used as the output signal X for evaluating short-term memory capacity.

Fig. 3
figure 3

a Measurement circuit used in experiments. Input data were preprocessed and injected into the STO through an arbitrary wave generator (AWG) and low-pass filter. Output voltage was measured with an oscilloscope after passing through the high-pass filter. Amplitude of output voltage was estimated using Hilbert transformation. Memory capacity was evaluated by comparing amplitude of output voltage with input data. b Example of sequential input-voltage pulses and c voltage output from STO. Intensity, offset, and pulse duration of input voltage were \(V_\mathrm{int}=100\) mV, \(V_\mathrm{offset}=250\) mV, and \(\Delta t=20\) ns, respectively (After Tsunegi et al. 2018a)

Full size image

Figure 3b, c shows examples of the input and output voltages for offset voltage \(V_\mathrm{offset}=250\) mV and \(\Delta t=20\) ns. The input voltage was 200 or 300 mV, and the corresponding oscillation frequency of the STO was 540 or 555 MHz, respectively. The output voltage exhibited a temporal change in magnitude, in accordance with the change in the input pulse voltage. The amplitude is the envelope of the oscillating voltage, as shown by the red curve in Fig. 3c. It was used to estimate the short-term memory capacity.

In our experiments, we used 3500 random bits in total, where the first 500 bits were used for the washout, the following 2000 (\(Z=2000\)) bits were used for learning, and the last 1000 (\(Z^{\prime }=1000\)) bits were used to estimate the short-term memory capacity. Hereafter, we call this sequence of 3500 bits a “single shot.”

Since the dynamics of the vortex core exhibited randomness due to thermal fluctuation, the initial conditions, as well as the amplitude noise in the output voltage, differed for every trial. Thus, the output voltage from the STO differed every run even when the same voltage pulses were used as input. Therefore, we repeated the single-shot experiment 60 times using fixed training and test data. The amplitude was averaged, with which the test data was also reconstructed. Using the average amplitude for both learning and testing should reduce the amplitude noise, leading to an increase in short-term memory capacity.

3.2 Short-Term Memory Capacity in Single STO

Figure 4a shows comparisons between the test (red solid line) and reconstructed (blue dotted line) data using 200 nodes in a single-shot experiment with delay \(D=1\), 2, or 3. For \(D=1\), the reconstructed data reproduced the test data almost perfectly, indicating that the STO remembered the input voltage applied one bit before the present pulse. In contrast, the ability to reconstruct data was low for \(D=2\) and 3. Using the averaging technique improved the reconstruction data for \(D=2\), as can be seen in Fig. 4b. These reconstructed data and Eq. (10) were used to evaluate the correlation coefficients.

Fig. 4
figure 4

Comparisons between test (red solid line) and reconstructed (blue dotted line) data for a single-shot and b averaged data. Delay D was 1, 2, and 3 from top to bottom (After Tsunegi et al. 2018a)

Full size image

Figure 5a illustrates the relationship between delay D and correlation \(\mathrm{Cor}(D)\) for the single-shot (red solid line) and averaged data (blue dotted line). The short-term memory capacities estimated from these data and Eq. (11) were nearly 1.0 for the single-shot experiment and 1.8 for the “averaged 60 times” experiment. These results indicate that reducing the amplitude noise of the output voltage is important for increasing short-term memory capacity.

Fig. 5
figure 5

a Square of correlation \(\mathrm{Cor}(D)\) between the test and reconstructed data for single-shot (red dotted) and averaged (blue solid) data as a function of delay D. b Dependence of memory capacity in circuit without (red triangles) and with (blue circles) STO on pulse duration \(\Delta t\) (After Tsunegi et al. 2018a)

Full size image

We performed the same experiment but with values of \(\Delta t\) other than 20 ns. The pulse duration dependency of the short-term memory capacity obtained from the averaged results is plotted in Fig. 5b by circles. The short-term memory capacity decreased monotonically with an increase in the pulse duration for the following reason. When a voltage pulse is applied to the STO, the vortex core starts to relax to an oscillation orbit (limit cycle) determined by the voltage. Now let us assume that a voltage pulse is applied at \(t=t_{0}\) and that the next pulse is applied at \(t=t_{0}+\Delta t\). If pulse width \(\Delta t\) is sufficiently greater than the relaxation time of the vortex core, the output voltage for \(t>t_{0}+\Delta t\) is not correlated to that for \(t<t_{0}\). Therefore, the short-term memory capacity decreases with an increase in the pulse width. The pulse width should thus be less than the relaxation time of the STO for reservoir computing. The relaxation time of the STO strongly depends on the type of oscillator. Roughly speaking, the relaxation time is of the order of \(1/(\alpha f)\), where \(\alpha \) and f are the damping constant and oscillation frequency, respectively (Taniguchi et al. 2017). The relaxation time of a vortex-type STO is of the order of \(10{-}100\) ns (Jenkins et al. 2016; Tsunegi et al. 2018b) whereas that of a macromagnetic STO is of the order of \(1{-}10\) ns (Kudo et al. 2010; Suto et al. 2011; Nagasawa et al. 2011). Evaluation of STO relaxation time will be a key issue for designing reservoir computing based on spintronics technology.

3.3 Contributions from Other Circuit Components

The definition used for short-term memory capacity in this work needs to be mentioned. The memory function of reservoir computing arises from the nonlinear response of the system to the input data. In the present system, not only the STO but also the other components in the circuit, such as the AWG and low-pass filter (Fig. 3a), exhibit nonlinear responses to input data. Therefore, the short-term memory capacity evaluated above should be, strictly speaking, regarded as that of the whole system, and includes the contributions from the other components of the circuit.

To validate the existence of the memory function in the STO, we also evaluated the short-term memory capacity of the system without the oscillator. The results are plotted in Fig. 5b by triangles. The short-term memory capacity of the circuit with the STO exceeded that of the circuit without the STO, proving that the STO has memory functionality.

3.4 Future Directions

Although the finite value of memory capacity found in this work supports the potential application of spintronics devices to artificial neural networks, the short-term memory capacity is still low compared with that of other systems such as a quantum reservoir with several qubits and virtual nodes (Fujii and Nakajima 2017). The low memory capacity of the present system is due to the trade-off between noise reduction of noise and capacity enhancement. As explained above, the memory of the past input voltage is stored in the amplitude of the output voltage. Noise in the amplitude of the output voltage reduces memory capacity. Therefore, the changes in the output voltage amplitude between neighboring nodes should be large enough to be distinguished from the noise. However, a large change in the output voltage amplitude between the neighboring nodes means fast relaxation, leading to a reduction in memory capacity. Therefore, solutions that further enhance memory capacity are needed.

A potential solution is to use an STO with delayed feedback (Khalsa et al. 2015; Tsunegi et al. 2016b), where the information of past input is naturally stored in the delayed feedback loop, resulting in an increase in short-term memory capacity (Riou et al. 2019; Yamaguchi et al. 2020). Another is to use frequency and/or phase locking of the STO by using forced or mutual synchronization (Marković et al. 2019; Tsunegi et al. 2019). This is because locking by synchronization leads to a reduction in the amplitude and/or phase noise and thus stabilizes the output voltage (Kaka et al. 2005; Mancoff et al. 2005; Zhou and Akerman 2009; Locatelli et al. 2015; Urazhdin et al. 2016; Awad et al. 2017; Tsunegi et al. 2018c). Investigating such solution is a future research direction in reservoir computing using spintronics technology.

4 Reservoir Computing with STO (Simulation)

In this section, we discuss the quantitative analysis of the figures-of-merit for reservoir computing using MTJ devices by employing macromagnetic simulation. Specifically, not only a reservoir computing system with single MTJ but also one with multiple MTJs is discussed (Furuta et al. 2018).

4.1 Simulation Methods

Figure 6a, b shows schematics of the system used for simulating reservoir computing using MTJs. As mentioned above, an MTJ contains an insulating tunneling barrier layer with two ferromagnetic layers. For ferromagnetic layer-1 (the reference layer), the magnetization direction is designed to be fixed. This can be done by the exchange bias effect using antiferromagnetic materials, such as PtMn and IrMn (Meiklejohn and Bean 1956), or magnetic anisotropy energy. Here, the magnetization direction of layer-1 was fixed perpendicular to the film plane. For ferromagnetic layer-2 (the free layer), the magnetization direction was not fixed and thus could be controlled by the current (Katine et al. 2000) or voltage (Shiota et al. 2012). The MTJ device resistance reflects the magnetization direction.

Fig. 6
figure 6

a Schematic of reservoir system using magnetization dynamics in an MTJ. b System with multiple MTJs. Magnetization direction of ferromagnetic layer-2 (\(\mathbf {s}_{2}\)) could be controlled by input bias voltage \(V_\mathrm{in}\); Magnetization direction of ferromagnetic layer-1 (\(\mathbf {p}\)) is fixed. c Input \(s_\mathrm{in}\), bias voltage \(V_\mathrm{in}\) input to MTJ device, and MTJ device resistance as function of time, which are typical characteristics during learning and evaluation processes. Virtual nodes [\(x_{k,1}\) to \(x_{k,N}\) during kth binary input] were defined as shown in figure. d MTJ device resistance as function of static input DC bias voltage. Black and red plots indicate resistance, when uniaxial anisotropy fields were 500 Oe and 1000 Oe, respectively. \(V_{0}\) and \(V_{1}\) are voltages that rendered device resistance constant (After Furuta et al. 2018)

Full size image

The magnetization dynamics in ferromagnetic layer-2 follows the LLG equation with STT given by Eq. (2), without thermal fluctuation in the ferromagnetic layers (Brown 1963). Here, \(\mathbf {p}\) and \(\mathbf {m}\) in Eq. (2) correspond to the unit magnetization vectors for ferromagnetic layers 1 and 2 in Fig. 6(a) and 6(b), respectively. The effective magnetic field in the present study is given by

$$\begin{aligned} \mathbf {H} = -H_{\mathrm{a}zz} m_{z} \mathbf {e}_{z}, \end{aligned}$$
(13)

where \(H_{\mathrm{a}zz}\) is a uniaxial perpendicular anisotropy field. The z-component of \(\mathbf {m}\) is denoted as \(m_{z}\), and \(\mathbf {e}_{z}\) is the unit vector parallel to the z-axis. In our definition, \(H_{\mathrm{a}zz} > 0\) (\(H_{\mathrm{a}zz} < 0\)) shows in-plane (perpendicular) magnetic anisotropy. The angular dependence of the STT in Eq. (2) is \(g(\theta )=1/(1+P^{2}\cos \theta )\) (Slonczewski 2005). The resistance of the MTJ varies with the relative angle between the spins in the free and pinned layers, \(R=1/G\) [see also Eq. (14)]

$$\begin{aligned} R = \frac{2R_\mathrm{AP}R_\mathrm{P}}{(R_\mathrm{AP}+R_\mathrm{P})+(R_\mathrm{AP}-R_\mathrm{P})(\mathbf {m}\cdot \mathbf {p})}. \end{aligned}$$
(14)

The time evolution of the MTJ resistance is characterized by sequential calculation using the fourth Runge–Kutta method. For evaluating the short-term memory and parity check capacities, an input pulse voltage, \(V_\mathrm{in}\), corresponding to the computational input, \(s_\mathrm{in}(=0\ \mathrm{or}\ 1)\), was applied to the MTJs, as depicted in Fig. 6c. Figure 6(a) and 6(b) shows the schematics of circuits with single and multiple MTJs, respectively. In this section, the physical parameters are \(H_{\mathrm{a}zz}=1000\) Oe, \(\alpha =0.009\), \(R_\mathrm{P}=210\) \(\Omega \), and \(R_\mathrm{AP}=390\) \(\Omega \). These values almost follow our previous experimental research (Miwa et al. 2014).

Figure 6c shows an example of MTJ device resistance under input voltage \(V_\mathrm{in}\). We used a pulse voltage with binary values of \(V_{0} (= -44\ \mathrm{mV})\) and \(V_{1} (= +44\ \mathrm{mV})\) as \(V_\mathrm{in}\). These binary values correspond to 0 and 1 in \(s_\mathrm{in}\), respectively, in the reservoir computing learning and evaluation processes. The pulse width (20 ns in Fig. 6c, for instance) corresponds to the discrete unit time step. Because the device resistance is scalar, the node dimension is simply one. However, the number of nodes can be increased by using virtual nodes (Appeltant et al. 2011; Nakajima et al. 2018). As shown in Fig. 6c, the virtual nodes \(x_{k,1}\) to \(x_{k,N}\) during the kth binary input are defined, where output signal \(x_{k,i}\) in the figure is the resistance with suffix \(i=1,2,\ldots ,N\) corresponding to the node number. These virtual nodes are further defined as a node vector \(\mathbf {x}_{k}\).

Figure 6d depicts the DC bias voltage dependence of the static MTJ device resistance. Under DC bias voltage conditions, the resistance was measured after the magnetization dynamics were damped. Under positive bias voltage conditions, the spin-polarized current flowed from the free layer to the pinned layer, and the STT induced auto-oscillation in \(\mathbf {m}\). The relative magnetization angle between \(\mathbf {p}\) and \(\mathbf {m}\) increased, and an antiparallel-like magnetization configuration was realized. This means that the device resistance increases when a positive bias voltage is applied. Under negative bias voltage conditions, a parallel-like magnetization configuration was induced, and the device resistance decreases. For the input pulse voltage depicted in Fig. 6c, the binary values \(V_{0}\) and \(V_{1}\) are defined as voltages that rendered device resistance constant. As shown in Fig. 6d, \(V_{0}\) and \(V_{1}\) depended on uniaxial magnetic anisotropy \(H_{\mathrm{a}zz}\).

Fig. 7
figure 7

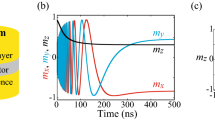
a Input \(s_\mathrm{in}^{\prime }\), test data \(y_\mathrm{STM}^{\prime }\) [Eq. (8) with \(D= 1\)], and reconstructed data \(y_\mathrm{R}^{\prime }\) used for evaluating the short-term memory task. b Input \(s_\mathrm{in}^{\prime }\), test data \(y_\mathrm{PC}^{\prime }\), (Eq. (9) with \(D=1\)), and reconstructed data \(y_\mathrm{R}^{\prime }\) used for evaluating parity check task. c Correlation using Eq. (10); integrated values are defined as short-term memory capacity (\(C_\mathrm{STM}\)). d Correlation using Eq. (10); integrated values are defined as the parity check capacity (\(C_\mathrm{PC}\)). Input-voltage pulse width was 20 ns, and number of virtual nodes was 50 (After Furuta et al. 2018)

Full size image

4.2 Short-Term Memory and Parity Check Capacities in Single STO

In this section, we present figures-of-merit for reservoir computing using a single MTJ device. The uniaxial magnetic anisotropy of the free layer \(\mathbf {m}\) was fixed: \(H_{\mathrm{a}zz} = 1000\) Oe. Recall that a positive value of \(H_{\mathrm{a}zz}\) means that the magnetic cell in the MTJ is in-plane magnetized. Figure 7 shows the simulated data used for evaluating the short-term memory and parity check capacities for a single MTJ. The input-voltage pulse width was 20 ns and the number of virtual nodes, N, was 50. Figure 7a shows typical simulation results for input \(s_\mathrm{in}^{\prime }\), test data for short-term memory task \(y_\mathrm{STM}^{\prime }\), and reconstructed data \(y_\mathrm{R}^{\prime }\) as a function of time. Similarly, Fig. 7b shows input \(s_\mathrm{in}^{\prime }\), test data for parity check task \(y_\mathrm{PC}^{\prime }\), and trained output \(y_\mathrm{R}^{\prime }\). Delay D in both figure was 1. The training and test data for the short-term memory task and parity check task are defined by Eqs. (7) and (12), respectively. The output was calculated using the simulated MTJ resistance (see Fig. 6c) and the weight. The weight was trivially calculated using the definitions given by Eq. (8). Figure 7c, d depicts the correlations [Eq. (10)] between the test and reconstructed data as a function of D. \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) are defined as the numerical integration of the correlation [see Eq. (11)] and as the capacity using training data for the short-term memory and parity check, respectively.

Fig. 8
figure 8

a, b Results of reservoir computing using single MTJ for short-term memory capacity (\(C_\mathrm{STM}\)), and parity check capacity (\(C_\mathrm{PC}\)) as a function of input-voltage pulse width; N is number of virtual nodes in MTJ. c, d Results of reservoir computing using multiple MTJs for \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) with seven MTJs (\(M=7\)) as function of input-voltage pulse width. Uniaxial magnetic anisotropy ratio (\(H_{\mathrm{a}zz, k+1} / H_{\mathrm{a}zz, k}\)) was 1.6 (After Furuta et al. 2018)

Full size image

Figure 8(a) and 8(b) shows the short-term memory \(C_\mathrm{STM}\) and parity check \(C_\mathrm{PC}\) capacities, respectively, as functions of the input-voltage pulse width with virtual nodes N. Both \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) increased with the pulse width until it reached \(\sim 20\) ns. They then remained nearly constant. When the pulse width is less than 20 ns, the change in the magnetization direction is very small, so the magnetization dynamics cannot work as a reservoir.

4.3 Short-Term Memory and Parity Check Capacities in Multiple STOs

When multiple MTJs are used for reservoir computing, higher figures-of-merit can be obtained. A schematic of a multiple-MTJ circuit for reservoir computing is depicted in Fig. 6b. MTJs are placed in parallel, and an identical pulse voltage is applied to all of them. Spatial multiplexing (Nakajima et al. 2019) is used to construct the nodes for reservoir computing. The node vector has \(M\times N\) elements, where M is the number of MTJs and N is the number of virtual nodes in an MTJ:

$$\begin{aligned} \mathbf {x}_{L,k} = \begin{pmatrix} x_{L,k,1} \\ \vdots \\ x_{L,k,N} \end{pmatrix},&\left( L = 1,2,\ldots , M \right) , \end{aligned}$$
(15)
$$\begin{aligned} \mathbf {x}_{k} \equiv \begin{pmatrix} x_{1,k,1}&\cdots&x_{1,k,N}&x_{2,k,1} \cdots&x_{2,k,N}&\cdots x_{M,k,N} \end{pmatrix}^\mathrm{t}, \end{aligned}$$
(16)

where “t” indicates a transposed vector, and \(x_{L,k,i}\) is the signal output from the Lth MTJ (\(L=1,2,\ldots ,M\)) at the ith node (\(i=1,2,\ldots ,N\)) in response to the kth binary data input (\(k=1,2,\ldots ,Z\)).

We tested various sets of uniaxial anisotropy \(H_{\mathrm{a}zz}\) of ferromagnetic layer-2 in each MTJ (see Table 1). For instance, when four MTJs were used and \(H_{\mathrm{a}zz, k}/H_{\mathrm{a}zz, k+1} = 2\), the uniaxial anisotropies of the MTJs were 1000 Oe, 500 Oe, 250 Oe, and 125 Oe. Such variations in anisotropy can be obtained by voltage-controlled magnetic anisotropy in the MTJs (Maruyama et al. 2009). In this study, thermal fluctuation in ferromagnetic layer-2 was neglected. For instance, thermal fluctuation energy at room temperature (26 meV) is negligibly small compared to magnetization energy \(M_\mathrm{s}H_{\mathrm{a}zz}\mathcal {V}/2\) (\(\sim 10\) eV) when \(H_{\mathrm{a}zz}\) = 1000 Oe. Here, \(M_\mathrm{s}\) and \(\mathcal {V}\) are the saturation magnetization and volume of the free layer and were assumed to be 1375 emu/c.c. and 23500 nm\({}^{3}\), respectively (Miwa et al. 2014). Therefore, thermal fluctuation is comparable to or less than the magnetization energy of ferromagnetic layer-2 for \(H_{\mathrm{a}zz} < 3\) Oe. In this region, simulation assuming the ground state is not very accurate, so a random magnetic field to reproduce the thermal fluctuation (Brown 1963) should be included in the simulation. Similar to the procedure for a single MTJ, the binary values \(V_{0}\) and \(V_{1}\), the voltage input to the MTJs, were determined as shown in Fig. 6d. Note that \(V_{0}\) and \(V_{1}\) vary as a function of the uniaxial anisotropy field, and the smallest absolute values of the saturation voltages are used for as \(V_{0}\) and \(V_{1}\) for reservoir computing with multiple MTJs, i.e., \(V_{0}\) and \(V_{1}\) are determined for the MTJ with the smallest uniaxial magnetic anisotropy field.

Table 1 Sets of uniaxial magnetic anisotropy used for reservoir computing with multiple MTJs
Full size table

We characterized \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) as functions of anisotropy ratio \(H_{\mathrm{a}zz, k}/H_{\mathrm{a}zz, k+1}\). In the simulation, the input-voltage pulse width was 20 ns, and the number of virtual nodes for each MTJ was 50 for all MTJs. The maximum value of \(C_\mathrm{STM}\) increased with the number of MTJs (M). Because each MTJ had a different uniaxial magnetic anisotropy field \(H_{\mathrm{a}zz}\), it had a different response speed to an external voltage/current. This variation in the response speed increased the \(C_\mathrm{STM}\) of the system. In contrast, the increase in \(C_\mathrm{PC}\) was insignificant compared to that in \(C_\mathrm{STM}\) because there was no electric and/or magnetic interaction between the free layers of the MTJs. For instance, we found that \(H_{\mathrm{a}zz, k} / H_{\mathrm{a}zz, k+1} = 1.6\) was the best condition for maximizing \(C_\mathrm{STM}\) for \(M=7\). As shown in Fig. 8c, the \(C_\mathrm{STM}\) was maximum around a pulse width of 20 ns. When the pulse width was smaller, the change in the magnetization direction due to the STT is too small for performing as a reservoir. When the pulse width was greater than 20 ns, the magnetization dynamics was almost completely damped during each unit time step, and such a condition is not preferable for reservoir computing. As shown in Fig. 8d, the best conditions are not the same for \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\). This is because a relatively long pulse is required to induce nonlinearity in the magnetization dynamics, in multiple MTJs.

4.4 Comparison with Echo-State Network

We used an echo-state network for comparison (Jaeger and Haas 2004; Jaeger 2001). An echo-state network is also a kind of RNN, in which the input-to-reservoir weight \(\mathbf {W}_\mathrm{in}\) and internal weights \(\mathsf {W}\) between nodes are random, whereas the reservoir-to-output weight is optimized. The node vector at time step k of the echo-state network is determined in terms of the node vector at the previous step and the input at time step k. The following function is used as a node vector of the echo-state network,

Fig. 9
figure 9

Plots showing \(C_\mathrm{STM}\) versus \(C_\mathrm{PC}\) in a MTJ system and b echo-state network. In MTJ system, pulse width and number of virtual nodes (N) of each MTJ were fixed to 20 ns and 50, respectively (After Furuta et al. 2018)

Full size image
$$\begin{aligned} \mathbf {x}_{\mathrm{ESN},k} = \tanh \left( \mathsf {W} \mathbf {x}_{k-1} + \mathbf {W}_\mathrm{in} s_{\mathrm{in},k} \right) . \end{aligned}$$
(17)

The hyperbolic tangent function is used for component-wise projection. Weights \(\mathsf {W}\) and \(\mathbf {W}_\mathrm{in}\) are given in a matrix and vector, respectively, in which the components are time-independent random values from \(-1\) to \(+1\). We normalized \(\mathsf {W}\) by dividing each component of \(\mathsf {W}\) by the spectral radius, which is the largest absolute value of the eigenvalues (singular value) of the weight matrix (Verstraeten et al. 2007). Weight \(\mathbf {W}_\mathrm{in}\) is also normalized by its spectral radius. The \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) obtained using a multiple MTJ system are plotted in Fig. 9a; the pulse width was 20 ns and the number of virtual node was 50 for each MTJ. The data points from top to bottom correspond to increase in \(H_{\mathrm{a}zz, k} /H_{\mathrm{a}zz, k+1}\) from 1.1 to 3.0. The \(C_\mathrm{STM}\) and \(C_\mathrm{PC}\) obtained using the echo-state network are shown in Fig. 9b. The data points from top to bottom correspond to increase the spectrum radius of the weight from 0.05 to 2.0. The results shown in Fig. 9 indicate that high-performance reservoir computing, similar to that of an echo-state network with 20–30 nodes, can be obtained for reservoir computing using 5–7 MTJs. In terms of the total number of virtual nodes in the system (\(M\times N\)), 35 nodes (\(7\times 5\)) in an MTJ system are comparable to 20–30 nodes in an echo-state network. Although \(C_\mathrm{PC}\) increased slightly with M, we can obtain a large \(C_\mathrm{PC}\) if there are magnetic and/or electrical interactions between the free layers in each MTJ.

5 Conclusion

In this chapter, we have described advances in brain-inspired computing devices based on spintronics technology. We have reviewed recent experimental and numerical work and reported our efforts in investigating the applicability of spintronics auto-oscillators (spin-torque oscillators, STOs) to recurrent neural networks. Spintronics devices have several attractive features for brain-inspired computing, such as low power consumption, applicability to high-density structures, a large output signal, and highly nonlinear and fast magnetization dynamics. Therefore, spintronics technology is promising for further development of artificial neural networks. However, the basic properties of spintronics devices, from the viewpoint of brain-inspired computing, have not been fully revealed yet. To prove the applicability of spintronics technology to computing, we need a deep understanding of magnetization dynamics in nanomagnets.

We have experimentally evaluated the short-term memory capacity of a reservoir computing with an STO. We have demonstrated the feasibility of learning and testing from output voltage by applying a time sequence of random voltage pulses to the STO. The short-term memory capacity obtained from the average output voltage was maximized to 1.8 under optimum conditions. Although this value includes the contribution not only from the STO but also from the other circuit components, the oscillator was shown to have a finite memory functionality. This indicates that it is important to reduce the amplitude noise in an STO applied to reservoir computing. The short-term memory capacity was increased by using a short pulse duration of 20 ns, which is comparable to the relaxation time (10–100 ns) of the oscillator. This indicates that it is also important to set the duration of the input pulses appropriately.

Using macromagnetic simulation, we demonstrated reservoir computing using the magnetization dynamics in MTJs. With reservoir computing using 5–7 MTJs, we can obtain performance similar to that of an echo-state network using hyperbolic tangent function with 20–30 nodes. Higher performance can be obtained by enabling magnetic and/or electrical interactions between the free layers in each MTJ.