Keywords

1 Introduction

Sewer network is an essential part of any urban infrastructure. The sewer network design consists of creating a suitable sewer layout that conforms to connect all buildings, street layouts, and local developing area. The alignment of sewer layouts is highly dependent on the location of sewage treatment plant or outlet, network size, and topography of the area. Finding the minimum length layouts among too many alternatives is the first step in designing a new urban sewer network. The capital cost of sewer network, installing, replacing, or modifying is very high. Reduction in the length of sewer line leads to a substantial saving in the capital cost. For this reason, significant researchers have attempted to the development of appropriate optimization techniques for sewer network design in recent years [1,2,3,4,5,6].

The sewer network design optimization problem is divided into two subproblems which are feasible layout selection and optimal component size determination. Due to the complex nature of the problem, most of the researchers have focused on the easier problem of component size optimization [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Only a few researchers have addressed the problem of feasible layout generation of networks by using different techniques of optimization [2,3,4,5,6, 11, 27,28,29,30].

This work describes a method for the selection of an optimal layout of a base sewer network. An algorithm generation of all spanning tree has applied to the generation of all minimum length layouts of a base sewer network. After that, all layouts are then sequenced in ascending order of total cumulative flow (Q) while the cost function of a layout based on that proposed by Walters and Smith [30] is applied to find the optimal sewer layouts. The proposed method is applied to two examples, and results are presented.

2 Feasible Sewer Layout Selection Method

The sewer network is a graph with specific properties. Therefore, it is necessary to review some basic definitions and principles of the graphs [31,32,33].

An undirected graph G = (V, E) consists of a set of objects V (V = v1, v2, …, vn) called vertices and another set E (E = e1, e2, …, e n ) called edges, such that each edge e ij is identified with an unordered pair (v i , v j ) of vertices. If in a graph G there is one path between every pair of vertices, G is a tree.

A weighted graph is a graph G in which every edge e has been allotted a real number w (e) called the weight of e. The weight of an edge in the sewerage system has been taken as its length.

A spanning tree of a graph G is a tree containing all vertices of G. A minimum spanning tree of an undirected weighted graph G is a spanning tree of which the sum of the edge weights is minimal.

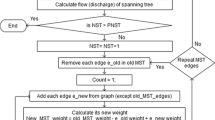
There are several algorithms for finding a minimum spanning tree (MST) of a graph. Kruskal’s algorithm is one of the optimized ways to generate a minimum length spanning tree for every connected undirected graph G. But layout optimization problem needs to generate all the spanning trees (layouts) of a base network (graph). Therefore, an algorithm generation of all spanning tree is introduced to find all sewer layouts (spanning trees) of a base network. The algorithm is based on the assumption that a base graph or sewer network, including all possible edges of the network, is available. In the base sewer network, there are n vertices (manholes or nodes) and m edges (sewers or links). A simplified representation of the algorithm is given below.

2.1 Algorithm—Generation of All Spanning Trees

Input—n, m, E, weights and nodal flow contribution;

n is the number of vertices, m is the number of edges, and E is the set of edges of graph G. Weight is the length of edges (sewers);

e_old is an edge of the current minimum spanning tree (MST), and e_new is a new edge from the remaining graph (base network);

Current_MST_weight is the total weight of current MST, and new_MST_weight is the total weight of newly generated MST;

2.2 Optimal Sewer Layout Selection

As described above, by using the generation of all spanning tree algorithm determined all sewer layouts of a base network. As a result, a large number of alternative layouts are available, and it is very difficult to identify directly the true optimal layout. Therefore, a strategy to sequence these alternatives needs to be introduced. Discharge q ij in ith link of the jth layout is calculated. After that, the sum of the cumulative discharges Q j in all links of the jth layout is calculated as shown in Eq. (1).

$$ Q_{j} = \sum\limits_{i = 1}^{i = n} {q_{ij} } $$
(1)

where n is the total number of links of the jth layout.

These layouts are then sequenced in ascending order by the sum of the cumulative discharges Q j . The layouts are then investigated for optimality in this sequence. Walters and Smith [30] proposed a cost function for the cost of network layout in terms of the length and concave function of flow rate of each link as given in Eq. (2):

$$ C_{j} = \sum\limits_{i = 1}^{n} {L_{ij} \sqrt {q_{ij} } } $$
(2)

where C j  = layout cost of the jth alternative, L ij  = link length, and q ij  = sewer discharge in the ith link of the jth layout.

The cost of each layout is calculated by using Eq. (2), and the optimal layout of a base network is selected where the cost of the layout is minimal.

3 Application

For the sewer network problem, manhole represents vertices and sewer pipes represent edges. The length of the sewer is taken as the weight of an edge.

The applicability of the procedures described in the previous section is tested in this section against two examples. The first example (network 1) that has been considered is a simple network, which is shown in Fig. 1. The network 1 consists of 6 nodes (vertices) and 10 links (edges), and the outlet is located at the node number 3. The wastewater contribution at each node of the network 1 is shown in Table 1. The second test example (sewer network of Sudarshanpura, Jaipur) is shown in Fig. 2. The Sudarshanpura base sewer network (network 2) consists of 105 nodes (vertices), 116 links (edges), and the outlet located at node number 0. Base graph data (link number, set of links, and its length) of network 2 are shown in Table 2. The wastewater contribution at each node of the network 2 is shown in Table 3.

Fig. 1
figure 1

Base layout of network 1

Full size image
Table 1 Nodal wastewater contribution for network 1
Full size table
Fig. 2
figure 2

Sudarshanpura base sewer network (network 2)

Full size image
Table 2 Base graph data for network 2
Full size table
Table 3 Nodal wastewater contribution for network 2
Full size table

The total number of nodes and links, set of links or edges, link length (weight), and nodal wastewater contributions are entered as an input detail for both the network.

Both problems network 1 and network 2 are solved by using above proposed procedure. The generation of all spanning tree algorithm is applied to find all layouts (spanning tree) of a base network; then, these layouts to be sequenced in ascending order of total cumulative flow Q (Eq. 1). After that, the cost function (Eq. 2) is applied to determine layout cost of the sequenced layouts. The top 4 optimal layouts of a network 1 are shown in Fig. 3.

Fig. 3
figure 3

Top for optimal layout of a network 1

Full size image

The results of network 2 are illustrated in Table 4. It is clearly seen that the layout cost (C) generally increases with the total cumulative flow (Q). The minimum cost of 13111.46 was obtained corresponding to the layout with cumulative flow value (Q) of 3642.78 l/s (Fig. 4). The layout with minimum cumulative flow value of 3639.13 l/s has the cost of 13170.85 (Fig. 5) which is 0.45% above the minimum cost layout. The proposed method for selection of global optimal layout is very convenient to implement on the sewer network problem. It may be concluded that minimum cumulative flow layout is near global optimal layout.

Table 4 Total cumulative flow versus layout cost comparison
Full size table
Fig. 4
figure 4

Optimal sewer layout of network 2

Full size image
Fig. 5
figure 5

Alternative sewer layout of network 2

Full size image

4 Conclusions

A method for the selection of an optimal layout of a base network is introduced, in which an algorithm is applied to generate all spanning trees of a network (graph). As large numbers of possible spanning trees are available, these spanning trees are sorted in ascending order of total cumulative flow (Q). Further, the cost function is applied to determine layout cost of the sorted layouts. The optimal layout was selected where the total cost of layout found to be minimal. It may be concluded that the total cost of alternative generally increases with the total cumulative flow. The applicability and efficiency of the proposed method for layout optimization of sewer networks were tested against two examples. The result revealed that proposed method gives an optimal solution of the sewerage network.