Abstract
In the present work, a fixed point result for generalized weakly contractive mapping in fuzzy metric space has been established. An example is cited to illustrate the obtained result.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction and Preliminaries
The concept of fuzzy metric spaces have been introduced in different ways by many authors. Among which, KM-fuzzy metric space, introduced by Kramosil and Michalek [2] and GV-fuzzy metric space, introduced by George and Veeramani [3], are two most widely used fuzzy metric spaces. KM-fuzzy metric space is similar to generalized Menger space [4]. George and Veeramani imposed a strong condition on the definition of Kramosil and Michalek for topological reasons. Several fixed point results in these fuzzy metric spaces can be found in [5, 7, 8, 10, 11].
Alber et al. extended the concept of Banach contraction to the weak contraction and established a fixed point result in Hilbert space [1]. There after B.E. Rhoades investigated this result in metric space [6]. Fixed point problem for weak contraction mapping have been investigated by many authors [12,13,14,15, 17,18,19,20,21,22,23,24]. In [9] Dutta et al. extended the results of Rhoades. Motivated by the works of [9, 16, 25], in the present work, a fixed point result in fuzzy metric space, introduced by George and Veeramani, is obtained and an example is added in the support of main result.
Definition 1.1
[4]. A continuous t-norm \(*\) is a binary operation on \(\left[ 0,1\right] \), which satisfies the following conditions:
-
(i)
\(*\) is associative and commutative,
-
(ii)
\(x*1=x,\) for all \(x\in \left[ 0,1\right] ,\)
-
(iii)
\(x*y\le u*v,\) whenever \(x\le u\) and \(y\le v\), for all \(x,y,u,v\in \left[ 0,1\right] ,\)
-
(iv)
\(*\) is continuous.
For example: (a) The minimum t-norm, \(*_{M}\), defined by \(x*_{M}y=\min \left\{ x,y\right\} \); (b) The product t-norm, \(*_{P}\), defined by \(x*_{P}y=x.y\), are two basic t-norms.
Definition 1.2
[3]. The triplet \(\left( X,M,*\right) \) is called fuzzy metric space if X is a non-empty set, \(*\) is continuous t-norm and M is a fuzzy set on \(X^{2}\times \left( 0,\infty \right) \) satisfying the following conditions:
- (i):
-
\(M\left( x,y,t\right) >0,\)
- (ii):
-
\(M\left( x,y,t\right) =1\) if and only if \(x=y,\)
- (iii):
-
\(M\left( x,y,t\right) =M\left( y,x,t\right) ,\)
- (iv):
-
\(M\left( x,z,t+s\right) \ge M(x,y,t)*M(y,z,s),\)
- (v):
-
\(M\left( x,y,.\right) :\left( 0,\infty \right) \rightarrow \left[ 0,1\right] \) is continuous,
for all \(t,s\in \left( 0,\infty \right) \) and \(x,y,z\in X.\)
In this paper, we use the notion of fuzzy metric space introduced by George and Veeramani.
Definition 1.3
[3]. Let \(\left( X,M,*\right) \) be a fuzzy metric space. Then
- (i):
-
A sequence \(\{x_{n}\}\subseteq X\) is said to converge to a point \(x\in X\) if
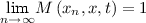 , for all \(t>0.\)
, for all \(t>0.\) - (ii):
-
A sequence \(\{x_{n}\}\subseteq X\) is called a Cauchy sequence if for each \(0<\varepsilon <1\) and \(t>0,\) there exists an \(N\in \mathbb {N}\) such that \(M\left( x_{n},x_{m},t\right) >1-\varepsilon ,\) for each \(m,n\ge N.\)
- (iii):
-
A fuzzy metric space is called complete if every Cauchy sequence in this space is convergent.
Lemma 1.1
[5]. Let \((X,M,*)\) be a fuzzy metric space. Then (X, M, .) is non-decreasing for all \(x,y \in X.\)
Lemma 1.2
[25]. If \(*\) is a continuous t-norm, and \(\{\alpha _{n}\}\), \(\{\beta _{n}\}\) and \(\{\gamma _{n}\}\) are sequences such that \(\alpha _{n} \rightarrow \alpha , \gamma _{n}\rightarrow \gamma \) as \(n\rightarrow \infty ,\) then \(\underset{k\rightarrow \infty }{\overline{\lim }}(\alpha _{k}*\beta _{k}*\gamma _{k})= \alpha *\underset{k\rightarrow \infty }{\overline{\lim }}\beta _{k} *\gamma \) and \(\underset{k\rightarrow \infty }{\underline{\lim }}(\alpha _{k}*\beta _{k}*\gamma _{k})= \alpha *\underset{k\rightarrow \infty }{\underline{\lim }}\beta _{k} *\gamma .\)
Lemma 1.3
[25]. Let \(\{f(k,.):(0,\infty )\rightarrow (0,1], k=0,1,2,........\}\) be a sequence of functions such that f(k, .) is continuous and monotone increasing for each \(k\ge 0.\) Then \(\underset{k\rightarrow \infty }{\overline{\lim }}f(k,t)\) is a left continuous function in t and \(\underset{k\rightarrow \infty }{\underline{\lim }}f(k,t)\) is a right continuous function in t.
2 Main Results
Theorem 2.1
Let \(\left( X,M,*\right) \) be a complete fuzzy metric space with an arbitrary continuous t-norm \('*'\) and let \(T:X\rightarrow X\) be a self mapping satisfying the following condition:
where \(\psi , \phi :(0,1]\rightarrow [0,\infty )\) are two functions such that:
- (i):
-
\(\psi \) is continuous and monotone decreasing function with \(\psi (t)=0\) if and only if \(t=1,\)
- (ii):
-
\(\phi \) is lower semi continuous function with \(\phi (t)=0\) if and only if \(t=1.\)
Then T has a unique fixed point.
Proof: Let \(x_{0}\in X.\) We define the sequence \(\{x_n\} \) in X such that \(x_{n+1}=Tx_{n},\) for each \(n\ge 0.\) If there exists a positive integer k such that \(x_{k}=x_{k+1},\) then \(x_{k}\) is a fixed point of T. Hence, we shall assume that \(x_{n}\ne x_{n+1},\) for all \(n\ge 0.\) Now, from (2.1)
Suppose that \(M(x_{n},x_{n+1},t) > M(x_{n+1},x_{n+2},t),\) for some positive integer n. Then from (2.2), we have
\(\psi (M(x_{n+1},x_{n+2},t))\le \psi (M(x_{n+1},x_{n+2},t))-\phi (M(x_{n+1},x_{n+2},t)),\) that is, \(\phi (M(x_{n+1},x_{n+2},t))\le 0,\) which implies that \(M(x_{n+1},x_{n+2},t)=1.\) This gives that \(x_{n+1}=x_{n+2},\) which is a contradiction.
Therefore, \(M(x_{n+1},x_{n+2},t) \le M(x_{n},x_{n+1},t)\) for all \(n\ge 0,\) and \(\{ M(x_{n},x_{n+1},t)\} \) is a monotone increasing sequence of non-negative real numbers. Hence, there exists an \(r>0\) such that  .
.
In view of the above facts, from (2.2), we have
\(\psi (M(x_{n+1},x_{n+2},t))\le \psi (M(x_{n},x_{n+1},t))-\phi (M(x_{n},x_{n+1},t)),\) for all \(n\ge 0,\)
Taking the limit as \(n\rightarrow \infty \) in the above inequality and using the continuities of \(\phi \) and \(\psi \) we have \(\psi (r)\le \psi (r)-\phi (r),\) which is a contradiction unless \(r=1.\) Hence
Next, we show that \(\{x_{n}\}\) is Cauchy sequence. If otherwise, there exist \(\lambda ,\, \epsilon >0\) with \(\lambda \in (0,1)\) such that for each integer k, there are two integers l(k) and m(k) such that \(m(k)>l(k)\ge k\) and
By choosing m(k) to be the smallest integer exceeding l(k) for which (2.4) holds, then for all \(k>0,\) we have
Now, by triangle inequality, for any s with \(0<s<\frac{\epsilon }{2},\) for all \(k>0,\) we have
For \(t>0,\) we define the function \(h_{1}(t)=\underset{n\rightarrow \infty }{\overline{\lim }}M\left( x_{l(k)+1},x_{m(k)+1},t\right) .\)
Taking \( \limsup \) on both the sides of (2.5), using (2.3) and the continuity property of \(*,\) by Lemma (1.2), we conclude that
By an application of Lemma (1.3), \(h_{1}\) is left continuous.
Letting limit as \(s\rightarrow 0\) in the above inequality, we obtain
Next, for all \(t>0,\) we define the function
\(h_{2}(t)=\underset{k\rightarrow \infty }{\underline{\lim }}M\left( x_{l(k)+1},x_{m(k)+1},t\right) .\)
In above similar process, we can prove that
Combining (2.6) and (2.7), we get
\(\underset{k\rightarrow \infty }{\overline{\lim }}M(x_{l(k)+1},x_{m(k)+1},\epsilon )\le 1-\lambda \le \underset{k\rightarrow \infty }{\underline{\lim }}M(x_{l(k)+1},x_{m(k)+1},\epsilon ).\)
This implies that
Again by (2.6),
For \(t>0,\) we define the function
Now for \(s>0,\)
\(M(x_{l(k)},x_{m(k)},\epsilon +2s) \ge M(x_{l(k)},x_{l(k)+1},s)*M(x_{l(k)+1},x_{m(k)+1},\epsilon )*M(x_{m(k)+1},x_{m(k)},s).\)
Taking \(\liminf \) both the sides, we have
\(\underset{k\rightarrow \infty }{\underline{\lim }}M(x_{l(k)},x_{m(k)},\epsilon +2s)\ge 1*\underset{k\rightarrow \infty }{\underline{\lim }}M(x_{l(k)+1},x_{m(k)+1},\epsilon ) *1\) \(=1-\lambda .\)
Thus,
Taking limit as \(s\rightarrow 0,\) we get \(h_{3}(\epsilon )\ge 1-\lambda .\) Combining (2.9) and (2.10) we obtain
Now,
Taking limit as \(k\rightarrow \infty \), we get
\(\psi (1-\lambda )\le \psi (1-\lambda )-\phi (1-\lambda ),\) which is a contradiction.
Thus, \(\{x_{n}\}\) is Cauchy sequence. Since X is complete, there exists \(p \in X\) such that \(x_{n}\rightarrow p\) as \(n\rightarrow \infty .\) Now,
Taking limit as \(n \rightarrow \infty ,\) we get
\(\psi (M(p,Tp,t))\le \psi (M(p,Tp,t))-\phi (M(p,Tp,t)),\)
which implies that \(\phi (M(p,Tp,t))=0,\) that is,
\(M(p,Tp,t)=1\) or \(p=Tp.\)
We next establish that fixed point is unique. Let p and q be two fixed points of T.
Putting \(x=p\) and \(y=q\) in (2.1),
\(\psi (M(Tp,Tq,t))\le \psi (\min {M(p,q,t),M(p,Tp,t),M(q,Tq,t)})-\phi (\min {M(p,q,t),M(q,Tq,t)})\) or, \(\psi (M(p,q,t))\le \psi (\min {M(p,q,t),M(p,p,t),M(q,q,t)})-\phi (\min {M(p,q,t),M(q,q,t)})\) or, \(\psi (M(p,q,t))\le \psi (M(p,q,t))-\phi (M(p,q,t))\) or, \(\phi (M(p,q,t))\le 0,\) or, equivalently, \(M(p,q,t)=1,\) that is, \(p=q.\)
The following example is in support of Theorem 2.1.
Example 2.1
Let \(X=[0,1].\) Let
for all \(x,y\in X\) and \(t>0,\) then \((X,M,*)\) is a complete fuzzy metric space, where \('*'\) is product t-norm. Let \(\,\,\psi ,\phi :(0,1]\rightarrow [0,\infty )\) be defined by \(\psi (s)=\frac{1}{s}-1\) and \(\phi (s)=\frac{1}{s}-\frac{1}{\sqrt{s}}.\) Then \(\psi \) and \(\phi \) satisfy all the conditions of Theorem (2.1). Let the mapping \(T:X\rightarrow X\) be defined by \(Tx=\frac{x}{2},\) for all \(x\in X.\)
Now, we will show that
where \(M(x,y)=\min \{M(x,y,t),\,M(x,Tx,t),\,M(y,Ty,t)\}\) and \(N(x,y)=\phi (\min \{M(x,y,t),\,M(y,Ty,t)\}).\) Herein;
and
Case (1): When \(0\le y\le \frac{x}{2}\) or \(2x < y\le 1,\) then
and
Obviously, in this case, (2.11) is satisfied.
Case (2): When \(\frac{x}{2}< y \le \frac{2x}{3},\) then
and
In this case, \(\frac{x}{2}\ge x-y\) and exponential function is an increasing function. Therefore, \(e^{\frac{x-y}{2t}} \le e^{\frac{x}{2t}}-e^{\frac{x-y}{t}}+e^{\frac{x-y}{2t}}\) and hence (2.11) is satisfied.
Case (3): When \(\frac{2x}{3}< y \le x,\) then
and
Since, in this case, \(\frac{x-y}{2}\le \frac{y}{4}\) and \(\frac{x}{2}\ge \frac{y}{2}\), (2.11) is satisfied.
Case (4): \(x<y\le 2x,\) then
and
Since, in this case, \(\frac{y}{2}\ge y-x,\) (2.11) is satisfied. Hence, all the conditions of Theorem (2.1) are satisfied. Thus, 0 is the unique fixed point of T.
References
Alber, Y.I., Guerre-Delabriere, S.: Principle of weak contractive mapes in Hilbert space. In: New Results in Operator Theory and its Applications, vol. 98. Birkhuser, Basel, pp. 7–22 (1997)
Kramosil, O., Michalek, J.: Fuzzy metric and statistical metric spaces. Kybernetica 11, 326–334 (1975)
George, A., Veeramani, P.: On some results in fuzzy metric space. Fuzzy Sets Syst. 64, 395–399 (1994)
Schweizer, B., Sklar, A.: Statistical metric spaces. Pac. J. Math. 10, 313–334 (1960)
Grabice, M.: Fixed points in fuzzy metric spaces. Fuzzy Sets Syst. 27, 385–389 (1988)
Rhoades, B.E.: Some theorems on weakly contractive maps. Nonlinear Anal. 47, 2683–2693 (2001)
Berinde, V.: Approximating fixed points of weak \(\phi \)-contractions. Fixed Point Theor. 4, 131–142 (2003)
Zhang, Q., Song, Y.: Fixed point theory for generalized \(\phi \)-weak contractions. Appl. Math. Lett. 22, 75–78 (2009)
Dutta, P.N., Choudhury, B.S.: A generalization of contraction principle in metric spaces. Fixed Point Theor. Appl. 1–8 (2008). Article ID 406368
Som, T., Choudhury, B.S., Das, K.P.: Two common fixed point results in fuzzy metric spaces. Internat. Rev. Fuzzy. Math. 6, 21–32 (2011)
Doric, D.: Common fixed point for generalized \((\psi \)-\(\phi )\)-weak contractions. Appl. Math. Lett. 22, 1896–1900 (2009)
Popescu, O.: Fixed point for \((\psi \)-\(\phi )\)-weak contractions. Appl. Math. Lett. 24, 1–4 (2011)
Karapinar, E.: Fixed point theory for cyclic weak \(\phi \)-contraction. Appl. Math. Lett. 24, 822–825 (2011)
Rouhani, B., Moradi, S.: Common fixed point of multivalued generalized \(\phi \)-weak contractive mappings. Fixed Point Theor. Appl. 1–13 (2010). Article ID 708984
Samet, B., Vetro, C., Vetro, P.: Fixed point theorems for \((\alpha \)-\(\psi )\)-contractive type mappings. Nonlinear Anal. 75, 2154–2165 (2012)
Choudhury, B.S., Konar, P., Rhoades, B.E., Metiya, N.: Fixed point theorems for generalized weakly contractive mappings. Nonlin. Anal. 74, 2116–2126 (2011)
Moradi, S., Farajzadeh, A.: On the fixed point of \((\psi \)-\(\phi )\)-weak and generalized \((\psi \)-\(\phi )\)-weak contraction mappings. Appl. Math. Lett. 25, 1257–1262 (2012)
Jamala, N., Sarwara, M., Imdad, M.: Fixed point results for generalized \((\psi \)-\(\phi )\)-weak contractions with an application to system of non-linear integral equations. Trans. A Razm. Math. Inst. 171, 182–194 (2017)
Aydi, H., Karapnar, E., Shatanawi, W.: Coupled fixed point results for \((\psi \)-\(\phi )\)-weakly contractive condition in ordered partial metric spaces. Comput. Math. Appl. 62, 4449–4460 (2011)
Aydi, H., Postolache, M., Shatanawi, W.: Coupled fixed point results for \((\psi \)-\(\phi )\)-weakly contractive mappings in ordered \(G\)-metric spaces. Comput. Math. Appl. 63, 298–309 (2012)
An, T.V., Chi, K.P., Karapnar, E., Thanh, T.D.: An extension of generalized \((\psi \)-\(\phi )\)-weak contractions. Int. J. Math. Math. Sci. 1–11 (2012). Article ID 431872
Latif, A., Mongkolkeha, C., Sintunavarat, W.: Fixed point theorems for generalized \(\alpha \)-\(\beta \)-weakly contraction mappings in metric spaces and applications. Sci. World J. 1–14 (2014). Article ID 784207
Jha, K., Abbas, M., Beg, I., Pant, R.P., Imdad, M.: Common fixed point theorem for \((\psi \)-\(\phi )\)-weak contraction in suzzy metric space. Bull. Math. Anal. Appl. 3, 149–158 (2011)
Luo, T.: Fuzzy \((\psi \)-\(\phi )\)-contractive mapping and fixed point theorem. Appl. Math. Sci. 8(148), 7375–7381 (2016)
Saha, P., Choudhury, B.S., Das, P.: Weak coupled coincidence point results having a partially ordering in fuzzy metric space. Fuzzy. Inf. Eng. 7, 1–18 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Tiwari, V., Som, T. (2018). Fixed Point Results for \((\phi ,\psi )\)-Weak Contraction in Fuzzy Metric Spaces. In: Ghosh, D., Giri, D., Mohapatra, R., Savas, E., Sakurai, K., Singh, L. (eds) Mathematics and Computing. ICMC 2018. Communications in Computer and Information Science, vol 834. Springer, Singapore. https://doi.org/10.1007/978-981-13-0023-3_26
Download citation
DOI: https://doi.org/10.1007/978-981-13-0023-3_26
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-0022-6
Online ISBN: 978-981-13-0023-3
eBook Packages: Computer ScienceComputer Science (R0)



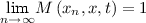 , for all
, for all