Numerical Simulation of Flows in a Channel with Impermeable and Permeable Walls Using Finite Volume Methods

Abstract

Laminar flows in a channel with permeable and impermeable walls are simulated using finite volume computational fluid dynamics (CFD). The CFD-simulated velocity profiles in the channel are compared with analytical solutions in the literature for impermeable walls (no-slip boundary condition) and with the authors’ analytical model for permeable walls (with slip boundary condition). The CFD results show very good agreement with the analytical solutions. A series of parametric studies show that when the slip coefficient α decreases from 4.0 to 0.1, the slip velocity at the channel-porous medium interface increases, but the velocity at the channel centre decreases, leading to a ‘flatter’ velocity profile, approaching that of a plug flow. This suggests a lower shear stress at the interface and a lower skin friction for a smaller slip coefficient. The lower skin friction leads to lower pressure drop per unit length along the channel. It is also found that when the wall permeability decreases, the slip velocity at the channel-porous medium interface decreases, leading to an increase in shear stress and skin friction, hence the increase in pressure drop per unit length along the channel. When the permeability k is less than a certain threshold, the slip velocity at the interface becomes very small and therefore, the shear stress and pressure drop values approach those of the no-slip boundary cases. The effect of the Reynolds number on the velocity profiles is insignificant for the range of values (0.5–7) studied in the chapter, but it has a much more pronounced effect on the pressure drops along the channel.

1 Introduction

Thermal heat from enhanced geothermal systems (EGS) has the ability to generate and dispatch baseload electricity without storage and with low carbon emissions. EGS reservoirs in hot dry rocks (HDR) are, in general, located at significant depths, commonly more than 3 km below the surface, and close to radiogenic heat sources (Mohais et al. 2011a). In their natural state, these rocks typically have temperatures at around 300 °C and usually have very low permeability. Extracting heat from an EGS requires a connected network of fractures in the rock mass through which fluid can be circulated and brought to the surface as very hot water. The fracture network is usually created by hydraulic fracturing, which creates new fractures and causes existing fractures to propagate (Mohais et al. 2011a, b). Cold working fluid, usually water, is injected into the fracture network through an injection well, flows through the fracture network, where it is heated by the surrounding rock and is then extracted through a production well. The heat in the extracted water can be used to generate electricity or can be used as a heat source for other applications.

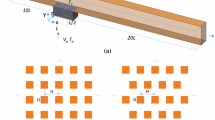
As a result of the hydro-fracturing process and the granular composition of the rocks, the walls of the fracture channels have permeable properties due to cracks and fissures of varying sizes in the channel wall (Christopher and Armstead 1978; Mohais et al. 2011b; Phillips 1991). The efficiency of the geothermal reservoir is highly dependent on the permeability of the rock fractures within the reservoir (Natarajan and Kumar 2012) and on the flows within the fracture channels, as demonstrated in Xu et al. (2015). Figure 1 shows idealised three-dimensional (3D) and two-dimensional (2D) schematic views of a flow channel with porous upper and lower walls. The walls are porous due to the cracks and fissures generated by the fracturing process. As the span-wise dimension of the fracture channels (z-direction in Fig. 1a) is always much larger than the height of the channel (y-direction in Fig. 1a, b) and variation of flow field in z-direction is assumed to be negligible, the channel flow is generally considered as a 2D flow as shown in Fig. 1b.

Fig. 1

a 3D and b 2D schematic view of channel flow with two porous medium walls

Several studies of fluid flows in channels with porous walls have been reported in the literature. In early studies of the flow at the interface between the channel and the porous medium, the velocity u in the x-direction in Fig. 1b, at the channel-porous medium interface was usually assumed to be zero (Mikelic and Jäger 2000). In fluid dynamics, this is known as the no-slip boundary condition.

Beavers and Joseph (1967) pioneered the investigation of the slip velocity at channel-porous medium interfaces. In an experiment, they compared fluid flow through a porous block with flow through a channel formed by an upper wall without flow through the wall and a lower permeable wall formed by the upper surface of the porous block. Flows were compared for various samples of two types of permeable material. This type of channel differs slightly from those in EGS in which the upper and lower walls channels (fractures) are porous (Fig. 1). Beavers and Joseph (1967) derived the boundary condition of the interface wall between the channel and the porous medium as

$$ \left. {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right|_{{y^{ + } = 0}} = \frac{\alpha }{\sqrt k }\left( {u_{\text{interface}} - u_{m} } \right), $$

(1)

where α is a dimensionless coefficient termed the slip coefficient or Beavers–Joseph coefficient. In Eq. (1), 0+ is a boundary limit point and y = 0+ means that du/dy values are calculated using the velocity u (velocity in x-direction) on the channel side but not the porous medium side. In Eq. (1), k is the absolute permeability of the porous medium (m²); u_interface is the fluid velocity u at the interface between the channel and the porous medium (m s⁻¹); u _m is the fluid velocity in the x-direction in the porous medium (m s⁻¹), given by Darcy’s law as below

$$ - \frac{{{\text{d}}p_{m} }}{{{\text{d}}x}} = \frac{\mu }{k}u_{m} , $$

(2)

where μ is the dynamic viscosity of the fluid (Pa s) and p _m is the pressure of the fluid in the porous medium (Pa).

Saffman (1971) further developed the generic velocity boundary condition for the fluid-porous medium interface based on the Beavers–Joseph boundary condition (Eq. 1). Saffman’s boundary condition (Nield 2009; Saffman 1971) is

$$ u_{\text{interface}} = \frac{\sqrt k }{\alpha } \frac{{\partial u_{\text{interface}} }}{\partial n} + O(k), $$

(3)

where O(k) is the average velocity in the porous medium (m s⁻¹), which can be neglected (Nield 2009). In Eq. (3), n denotes the direction normal to the fluid-porous medium interface. Again ∂u_interface/∂n is calculated on the channel side but not the porous medium side. The Beavers–Joseph boundary condition is a special case of Saffman’s boundary condition (Nield 2009; Saffman 1971) for channel flows. Saffman’s modification of the Beavers–Joseph condition has been further confirmed by theoretical studies such as Mikelic and Jäger (2000).

In a later study, Jones (1973) pointed out that the Beavers–Joseph boundary condition for generic cases should be

$$ \left. {\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)} \right|_{{y^{ + } = 0}} = \frac{\alpha }{\sqrt k }\left( {u_{\text{interface}} - u_{m} } \right) $$

(4)

meaning that the left-hand side of the equation should be the shear strain rate for generic cases. In Eq. (4), v is the velocity component in y-direction. It can be seen that the Beavers–Joseph condition is a special case of Jones’ condition, for a one-dimensional flow, ∂v/∂x = 0.

For the non-dimensional slip coefficient α in Eqs. (1), (3) and (4), Beavers and Joseph (1967) found that values of α depend on the structure of the porous material at the fluid-porous medium interface and materials with similar permeability may have, significantly, different slip coefficients but are independent of the fluid viscosity (Nield 2009). In the Beavers and Joseph (1967) study, for foametal with average pore sizes of 0.00406 m (0.016 in.), 0.00864 m (0.034 in.) and 0.0114 m (0.045 in.), the values of α are 0.78, 1.45 and 4.0, respectively; while, for aloxide with average pore sizes of 0.0033 m (0.013 in.) and 0.00686 m (0.027 in.), the value of α is 0.1, for both pore sizes. The influence of the fluid (water, oil and gas) on the value of α was found to be insignificant, whereas α is very sensitive to the nature of the porous interface (Beavers et al. 1974). A later numerical study by Larson and Higdon (1986) concluded that the value of α is sensitive to microscopic changes in the definition of the interface implying that it is not possible to define a consistent value of α for any media. The numerical studies of Sahraoui and Kaviany (1992) shows that α depends on porosity, Reynolds number (Re), channel height, choice of interface, bulk flow direction and interface structure. Another numerical study (Liu and Prosperetti 2011) shows that α values for pressure-driven and shear-driven flows are somewhat different and α values depend on the Reynolds number.

Several numerical studies of channel flows with porous media boundary conditions have been reported in the literature. One of the earliest, Berman (1953), used the perturbation method to solve the Navier–Stokes equations to describe the flow in a channel with a rectangular cross section and two equally porous walls. The velocity u at the channel-porous medium interface is taken as zero (no-slip condition) and the vertical velocity at the interface is assumed to be constant. Terrill and Shrestha (1965) used the perturbation method to solve the Navier–Stokes equations for laminar flows through parallel and uniformly porous walls. The boundary conditions in their study are similar to those in Berman (1953); the u velocities at the channel-porous medium interface are zero and the vertical velocities are constant but different for the two porous walls. Granger et al. (1989) obtained the analytical solutions of the Navier–Stokes equations for both a rectangular channel with one porous wall and a porous tubular channel. They found that the velocity u profile of the flow in porous channels may be considered parabolic and there is no pressure profile across the width of the channel. Recently, Herschlag et al. (2015) obtained the analytical solution for the flow in a channel with high wall permeability. The boundary conditions at the channel walls are no-slip for axial velocity and Darcy’s law for the vertical velocity.

The analytical studies reviewed above are for cases in which there are vertical flows at the channel-porous medium interfaces and the axial velocities at the channel-porous medium interface are assumed to be zero. This no-slip velocity condition is not realistic for fracture channels in EGS or similar systems. Mohais et al. (2011a, b) used the perturbation method to solve the Navier–Stokes equations to provide an analytical solution for laminar flow in a channel with porous walls and non-zero axial velocity at the fluid-porous media interface. For a channel with walls that contain small fissures, cracks and granular material, the axial velocity profile in the channel can be affected by factors such as the slip boundary coefficient, permeability and the channel width (Mohais et al. 2011a, b; Tian et al. 2012).

This chapter reports computational fluid dynamics (CFD) simulations of fluid flows in a single horizontal fracture sandwiched between two equally porous media, in the context of an EGS. Little research has been reported in modelling this problem using the finite volume approach.

The first objective is to compare the velocity profiles predicted by CFD with analytical solutions (Mohais et al. 2011a, b). To the authors’ knowledge, validations of these analytical solutions of flow velocity profiles in a channel (Mohais et al. 2011a, b) have not been investigated using numerical models. These validations will assist the development of other complex models of channel flows in future research.

The second objective is to investigate the influence of parameters such as slip coefficient α, Reynolds number, permeability and channel height on the velocity profiles and pressure drops in the channel flows. Of particular interest are the pressure drops in the channel flows under different conditions as they are not available in the analytical solutions reported in Mohais et al. (2011a, b).

2 Numerical Methods

2.1 CFD Domain and Boundary Conditions

In this study, laminar water flow is simulated in a 2D channel with a height of 2h. The channel is contained between two equally porous media, as illustrated in Fig. 1b. ANSYS/Designmodeler 17.2 was used to generate the CFD domain. Figure 2 is a schematic diagram of the domain and boundary conditions of the single fracture channel model. To reduce the computational time for the simulations, the CFD domain is half of a single channel with a symmetric boundary at the bottom, as shown in Fig. 2, and thus the height of the half-channel modelled is h. Following the work of Mohais et al. (2011b), two values of h(0.001 m and 0.0001 m) were tested in the study; these values are commonly used in modelling channel flows in EGS reservoirs. The Reynolds numbers for the flows vary from 0.5 to 7.0 as the analytical solutions of Mohais et al. (2011a, b) hold for Re < 7. The Reynolds number of the flow, Re, is defined in this case as

Fig. 2

The boundary conditions of the CFD model of a single fracture (not to scale)

$$ Rew = \frac{{2h\rho u_{\text{ave}} }}{\mu }, $$

(5)

where u_ave is the average velocity u of the flow in the channel (m s⁻¹), 2h is the full height of the channel (m) and ρ is the density of fluid (kg m⁻³) (water in this study).

In the x-direction, the periodic boundary condition is imposed with a mass flow rate of u_ave. The values of u_ave are calculated using Eq. (5) with corresponding Reynolds number Re and channel height 2h, for each case. The length of the channel L is 0.08 m for h = 0.001 m and 0.01 m for h = 0.0001 m. The fluid in the channel is water at 25 °C. The dynamic viscosity of water is 0.0008899 Pa s and the density of water is 997 kg m⁻³.

At the channel-porous medium interface, the velocity u of the fluid is imposed using the analytical equation developed by Mohais et al. (2011b). The porous walls are assumed to be saturated, i.e. there is no fluid flow across the interface boundary. The boundary conditions at the channel-porous medium interface used in the study are

$$ v_{\text{interface}} = 0 $$

(6)

$$ u_{\text{interface}} = \left. {u_{\text{ave}} f^{\prime } \left( {y^{*} } \right)} \right|_{{y^{ + } = 1}} = \left. {u_{\text{ave}} \left( {f_{0}^{\prime } \left( {y^{*} } \right) + Rew\,f_{01}^{{\prime }} \left( {y^{*} } \right)} \right)} \right|_{{y^{ + } = 1}} , $$

(7)

where v_interface is the fluid velocity in the y-direction at the channel-porous medium interface and u_interface is the fluid velocity in the x-direction at the channel-porous medium interface. In Eq. (7), y^* is the normalised distance in y-direction defined as y^* = y/h. Rew in Eq. (7) is the Reynolds number of fluid at the channel-porous medium interface and is calculated as in Mohais et al. (2011b)

$$ Rew = \frac{{2h\rho u_{\text{interface}} }}{\mu }. $$

(8)

In Eq. (7), f₀(y^*) and f₁(y^*) are determined as in Mohais et al. (2011b)

$$ f_{0} \left( {y^{*} } \right) = y^{*3} \left( {\frac{ - 1}{{2\left( {1 + 3\emptyset } \right)}} + y^{*} \frac{3 + 6\emptyset}{2 + 6\emptyset}} \right) $$

(9)

$$ \begin{aligned} f_{1} \left( {y^{*} } \right) & = - \frac{{y^{*7} }}{2520}\left( {\frac{9}{{\left( {1 + 3\phi } \right)^{2} }}} \right) + \frac{{y^{*3} }}{6}\left( {\frac{{9 \left( {7\phi + 1} \right)}}{{140\left( {1 + 3\phi } \right)^{3} }}} \right) \\ & \quad + y^{*} \left( {\frac{1}{{280\left( {1 + 3\phi } \right)^{2} }} - \frac{{3\left( {7\phi + 1} \right)}}{{280\left( {1 + 3\phi } \right)^{3} }}} \right), \\ \end{aligned} $$

(10)

where $\phi = \sqrt k /\left( {\alpha h} \right)$.

The CFD package, ANSYS/CFX 17.2, was used for all steady-state simulations based on the Navier–Stokes equations. The steady state Navier–Stokes equations for incompressible flows are

$$ {\varvec{\nabla }} \cdot {\mathbf{U}} = {\mathbf{0}} $$

(11)

$$ {\varvec{\nabla }} \cdot \left( {{\mathbf{UU}}} \right) = - \frac{{{\varvec{\nabla }}p}}{\rho } + {\varvec{\nabla}} \cdot \left\{ {\frac{\mu }{\rho }\left[ {{\varvec{\nabla }}{\mathbf{U}} + \left( {{\varvec{\nabla }}{\mathbf{U}}} \right)^{T} - \frac{2}{3} {\varvec{\nabla }} \cdot {\mathbf{IU}}} \right]} \right\} + {\mathbf{G}}, $$

(12)

where G is the source term due to gravity and I is the identity matrix. U in Eqs. (11) and (12) is velocity vector. Following the work of Mohais et al. (2011b), gravity has negligible effects on the flows and therefore is neglected in this chapter. ANSYS/CFX is a finite volume solver. The fourth-order Rhie–Chow option was used for the velocity pressure coupling. The high-resolution scheme was used for advection terms. A double precision version of the solver was employed to ensure the accuracy of the CFD results. The maximum residual target was set at 1.5 × 10⁻⁶ for all simulations.

2.2 CFD Mesh and Mesh-Independent Test

ANSYS/meshing was used to generate the CFD mesh. A grid independence test was conducted for the case for h = 0.001 m, Re = 0.5 and α = 1. An initial structured mesh of 700 (in the streamwise direction, x) × 50 (height, y) was generated and then refined to a mesh of 1000 × 80, and further refined to a mesh of 1500 × 120. Mesh independence was checked by comparing the fluid velocity profile along periodic boundary 1 (indicated as the red line in Fig. 3).

Fig. 3

Mesh at periodic boundary 1 for h = 0.001 m

Figure 4 shows the comparison of normalised velocity u profiles for h = 0.001 m, α = 1, Re = 0.5 and k = 10⁻⁸ m², for three mesh systems. The velocity u is normalised by the average velocity u_ave.

Fig. 4

Mesh independence test based on h = 0.001 m, α = 1, Re = 0.5 and k = 10⁻⁸ m²

All three meshes give almost identical results. The maximum difference in the results obtained from the 1000 × 80 mesh and the 1500 × 120 mesh is less than 1%. For h = 0.001 m, the 1000 × 80 structured mesh was used for all other simulations. Figure 3 shows the mesh nodes at periodic boundary condition 1 for this case. For h = 0.0001 m, a similar mesh independence test was conducted and the 1200 × 80 structured mesh was used for the simulations.

3 Results and Discussion

The CFD flow profiles for the channel with impermeable walls are reported in Sect. 3.1. The no-slip boundary (u_interface = 0) condition was imposed on the channel-porous medium interface. The purpose of reporting results for this boundary condition is twofold. The first is to verify the CFD results by comparing the predicted velocity profiles with the analytical solutions of Potter et al. (2016), and the second is to examine the differences between the pressure drop values of the slip boundary cases with those of the no-slip boundary conditions.

In Sects. 3.2–3.6, a series of parametric studies are reported for the flows in the channels with permeable walls. The slip boundary conditions calculated using Eq. (7) in Mohais et al. (2011b) were used to calculate the slip velocity (u_interface) at the channel-porous medium interface. The key parameters influencing the velocity profiles and pressure drop in the channel, including Re number, slip coefficient α, permeability k and channel height h are investigated using the CFD model.

In Sect. 3.7, we compare the slip velocities predicted by Eq. (7) and by Saffman’s boundary condition (Eq. 3) using the ∂u/∂n values predicted by CFD.

3.1 Flow and Pressure Drop in Channels with No-Slip Walls

Flows in channels with impermeable walls are simulated by imposing the no-slip boundary condition at the channel-porous medium interface. Table 1 lists the pressure drop per unit length, −∆p/L (Pa m⁻¹), predicted by CFD for the no-slip boundary condition, which is defined as

Table 1 CFD predicted −∆p/L values for different cases

$$ \frac{ - \Delta p}{L} = \frac{{ - \left( {p_{2} - p_{1} } \right)}}{L}, $$

(13)

where p₂ and p₁ are the area-averaged static pressures at periodic boundary 2 and 1 (Fig. 2), respectively. In Eq. (13), L denotes the length of the channel (m). Note, in our model, p₁ is always higher than p₂ in this pressure-driven flow.

The velocity profiles predicted by CFD in the channel with the no-slip boundary condition are verified by comparing them with the analytical solutions for laminar channel flows (Potter et al. 2016)

$$ u(y) = \frac{1}{2\mu }\frac{{{\text{d}}y}}{{{\text{d}}x}}\left( {y^{2} - 2hy} \right). $$

(14)

Figure 5 shows a comparison of the CFD-predicted velocity profile with the analytical solution of Eq. (14) for the case Re = 0.5 and h = 0.0001 m. The CFD model performs very well; the velocity profiles obtained from the two methods are almost identical with the maximum difference between them of about 0.7%. The same conclusion can be drawn for the other three cases: Re = 5 and h = 0.0001 m, Re = 0.5 and h = 0.001 m and Re = 5 and h = 0.001 m.

Fig. 5

Verification of CFD-predicted velocity profile against the analytical solution of Eq. (14) (Potter et al. 2016), no-slip boundary, h = 0.0001 m and Re = 0.5

3.2 Effect of Slip Coefficient on the Velocity Profiles

Figure 6 shows the CFD-predicted velocity u profiles normalised by the average velocity u_ave with varying values of α and Re = 0.5, h = 0.001 m and k = 10⁻⁸ m². In this case, the CFD results are compared with the solution of the analytical model given in Mohais et al. (2011b). The analytical model of Mohais et al. (2011b) is

Fig. 6

Comparison of CFD and analytical results (Eq. 3) for flows with walls with varying α values and Re = 0.5, h = 0.001 m, k = 10⁻⁸ m²

$$ f\left( {y^{*} } \right) = f_{0} \left( {y^{*} } \right) + Rew\,f_{1} \left( {y^{*} } \right), $$

(15)

where f₀(y^*) and f₁(y^*) are given in Eqs. (9) and (10), respectively.

The CFD predictions and the analytical solutions are almost identical for all cases shown in Fig. 6. The maximum difference between the CFD results and the analytical solutions for the cases shown in Fig. 6 is less than 1%. This very good agreement confirms the analytical solutions of velocity profiles in the channel derived by Mohais et al. (2011b).

As shown in Fig. 6, all the velocity curves are parabolic as expected for the channel flow (Mohais et al. 2011b). As the values of α increases from 0.1 to 4, the normalised velocity u at the channel-porous medium interface decreases from 0.75 (α = 0.1) to 0.0706 (α = 4). The normalised velocity at the channel centre line decreases as the value of α increases.

Figure 7 compares the CFD prediction with the analytical solutions of the profiles of normalised fluid velocity u with varying values of α and Re = 5, h = 0.001 m and k = 10⁻⁸ m⁻². The variations in u_interface for different α values and Re = 5 are very similar to those for Re = 0.5, with the normalised velocity u at the wall decreasing from 0.756 when α = 0.1 to 0.0786 when α = 4. The velocity at the channel-porous medium interface for α = 0.1 and Re = 5 in Fig. 7 is 0.757, compared with 0.751 for the Re = 0.5. The slightly higher interface velocity for Re = 5 is due to its higher corresponding Rew (Eq. 15), which is 3.78 compared with 0.375 for Re = 0.5 (shown in Fig. 6). The normalised velocity u at the channel centre line decreases as the value of α increases. This is not surprising as the mass flow rates of all the cases in Fig. 6 are the same. For these incompressible flows, the increase in velocity u at the region near the channel-porous medium interface needs to be balanced by the decrease of velocity u at the centre.

Fig. 7

Comparison of CFD and analytical results for flows with walls of varying α values and Re = 5, h = 0.001 m, k = 10⁻⁸ m²

Figure 8 compares the CFD and analytical results for flows in a narrower channel with h = 0.0001 m at Re = 0.5 and varying α values. When α = 0.1, the velocity profile is close to a vertical line, i.e. the fluid velocity at the channel-porous medium interface is close to the flow velocity at the channel centre line, similar to the profile of a plug flow. When α increases to 1 and then to 4, the fluid velocity at the interface decreases and the flow at the channel centre line increases. Compared with the results shown in Fig. 6, for h = 0.001 m and the same Re number, k value and α value, the fluid velocities at the channel-porous medium interface for h = 0.0001 m are higher. Again, this is caused by the higher Rew values for the cases shown in Fig. 8 than those shown in Fig. 6. The profiles of normalised velocity for h = 0.0001 m at Re = 5 with varying α values are given in Fig. 9. These profiles are very similar to those of the Re = 0.5 cases shown in Fig. 8, suggesting that the velocity profiles become insensitive to the Reynolds number.

Fig. 8

Comparison of CFD and analytical results for flows with walls of varying α values and Re = 0.5, h = 0.0001 m, k = 10⁻⁸ m²

Fig. 9

Comparison of CFD and analytical results for flows with walls of varying α and Re = 5, h = 0.0001 m, k = 10⁻⁸ m²

3.3 Effect of α Values on the Pressure Drops

The effect of the slip coefficient, α, on the pressure drop per unit length, −∆p/L, in the channel is investigated for channel heights of h = 0.001 m and h = 0.0001 m. As shown in Fig. 10, for both Re = 5 and Re = 0.5 with h = 0.001 m, the −∆p/L value is higher for a higher value of α. In other words, the higher the α value, the higher is the head loss in the channel flow. Please note that the pressure drops in the porous walls are not calculated in the current chapter. To calculate the total energy required to push the water through the channel, the porous walls should be included in the CFD domain.

Fig. 10

Effect of α values on the pressure drop per unit length −∆p/L when h = 0.001 m, k = 10⁻⁸ m²

For Re = 0.5 and h = 0.001 m, the −∆p/L value predicted by CFD for the no-slip boundary case is 0.594 Pa m⁻¹ (in Table 1). As shown in Fig. 10, the −∆p/L value of 0.15 Pa m⁻¹ for α = 0.1 is 25% of that for the corresponding no-slip boundary case. The −∆p/L value of 0.46 Pa m⁻¹ for α = 1 is 77.4% of that for the no-slip boundary case. The −∆p/L value of 0.55 for α = 4 is about 93% of that for the no-slip boundary case.

For the Re = 5 cases in Fig. 10, the −∆p/L value predicted by CFD for the no-slip boundary, when h = 0.001 m, is 5.94 Pa m⁻¹. With the slip boundary condition, the −∆p/L value is 1.45 Pa m⁻¹ for α = 0.1, which is 24.4% of that of the no-slip boundary case. The −∆p/L value approaches 5.94 Pa m⁻¹ as α increases and when α = 4, the value is 5.47 Pa m⁻¹, which is 92% of that of the no-slip boundary case.

The effect of α values on the pressure drop per unit length in the channel is much more pronounced when h = 0.0001 m (Fig. 11). For Re = 5 and h = 0.0001 m, the −∆p/L value of the no-slip boundary is 5940 Pa m⁻¹ (Table 1). With the slip boundary condition, for α = 0.1, the value is 191 Pa m⁻¹, which is 3.2% of that of no-slip boundary case, and for α = 4, the −∆p/L value is 3277 Pa m⁻¹, about 55% of that of no-slip boundary case. Similar trends can be observed for Re = 0.5 and h = 0.0001 m. The −∆p/L value of the no-slip boundary is 594 Pa m⁻¹, while the value of −∆p/L for α = 0.1 is 19 Pa m⁻¹ and for α = 4 is 338 Pa m⁻¹, which are 3.2 and 57%, respectively, of the no-slip boundary case.

Fig. 11

Effect of α values on the pressure drop per unit length −∆p/L when h = 0.0001 m, k = 10⁻⁸ m²

For both Re = 5 and Re = 0.5 cases, when h = 0.001 m (Fig. 10), the pressure drop per unit length under the slip boundary condition can result in up to a 75.6% (α = 0.1) reduction compared with the pressure drop per unit length for the non-slip boundary cases. When h = 0.0001 m, however, the slip boundary condition can result in up to a 96.8% (α = 0.1) reduction in pressure drop per unit length compared with the non-slip boundary condition results. The reduction in pressure drop per unit length for the slip boundary condition can be attributed to the reduction in shear stress at the channel-porous medium interface. For this channel flow, the shear stress at the channel-porous medium interface can be calculated as

$$ \tau_{\text{interface}} = \mu \left. {\frac{\partial y}{\partial x}} \right|_{\text{interface}} . $$

(16)

It is obvious from Figs. 6, 7, 8 and 9 that lower values of α lead to higher slip velocities at the channel-porous medium interface and lower velocity at the centre. This leads to ‘flatter’ velocity profiles and lower velocity gradients ∂u/∂y at the channel-porous medium interface and hence, based on Eq. (16), lower shear stress at the interface. This reduction in shear stress contributes to the reduction of skin friction and, in turn, reduction in the pressure drop per unit length along the channel.

3.4 Effect of Permeability k on the Velocity Profiles

Figure 12 shows the velocity profiles of flows in the channel for different permeability k values of the porous medium and for Re = 0.5, h = 0.001 m and α = 1. For lower permeability values (k = 10⁻¹⁰ m² and k = 10⁻¹² m²), the normalised u velocities at the channel-porous medium interface are as small as 0.033 and 0.003, respectively, leading to very small Rew values of 0.0149 and 0.00163, respectively. As the permeability k increases from k = 10⁻⁸ m² to k = 10⁻⁶ m², the normalised velocity u at the channel-porous medium interface increases from 0.2327 to 0.7506, while the normalised velocity u at the channel centre line decreases from 1.38 to 1.12 due to the conservation of mass flow rate.

Fig. 12

Effect of permeability on the velocity profiles for Re = 0.5, h = 0.001 m, α = 1

When the Re number increases from 0.5 to 5, the effect of permeability values on the velocity profiles is similar to the Re = 0.5 cases, i.e. higher permeability causes higher slip velocity at the channel-porous medium interface (Fig. 13). It is noticeable that for cases with the same permeability, the normalised slip velocity for Re = 5 (Fig. 13) is higher than that for Re = 0.5 (Fig. 12).

Fig. 13

Effect of permeability k on the velocity profiles for Re = 5, h = 0.001 m, α = 0.1; units of k (m²)

The effects of permeability k on the velocity profiles were also investigated for cases when h = 0.0001 m. Figure 14 shows the velocity profiles of low Re (i.e. Re = 0.5) and different permeability values. The profiles in Fig. 14 are comparable with those in Fig. 13 even though the latter are for a high Reynolds number of Re = 5 in a wider channel with h = 0.001 m. The reason for these similar profiles is that the same $\phi$ value $\left( {\phi = \sqrt k /(\alpha h)} \right)$ is obtained for all cases shown in these two figures even they have different Re and h values, which theoretically would lead to the same profile (see Eq. 7). On the other hand, the effect on the velocity profiles of Re ranging from 0.5 to 5 is not significant. This can be confirmed by comparing the velocity profiles for a higher Re(Re = 5), shown in Fig. 15, to those of a lower Re(Re = 0.5), shown in Fig. 14, with all other parameters unchanged. Nevertheless, more discussion about the effect of Re on the velocity profiles can be found in Sect. 3.6.

Fig. 14

Effects of permeability k on the velocity profiles for Re = 0.5, h = 0.0001 m, α = 1; units of k (m²)

Fig. 15

Effects of permeability k on the velocity profiles for cases of Re = 5, h = 0.0001 m, α = 1; units of k (m²)

3.5 Effect of Permeability k on the Pressure Drop Per Unit Length

Figures 16 and 17 show the variation of pressure drop per unit length −∆p/L for the channel with permeable walls and varying permeability, k. As the permeability k decreases, there is an increase in pressure drop per unit length, −∆p/L, for all the cases shown. This again can be explained by the fact that lower permeability results in lower slip velocity at the interface and hence a higher wall shear stress and skin friction, and the increase in skin friction consequently leads to an increase in the pressure drop, as discussed above.

Fig. 16

Effect of permeability k on the pressure drop per unit, −∆p/L, in the channel h = 0.001 m, α = 1

Fig. 17

Effect of permeability k on the pressure drop per unit, −∆p/L, in the channel h = 0.0001 m, α = 1

It is also noticeable in Figs. 16 and 17 that, when the permeability is less than a certain threshold (and any further decrease in k will not significantly increase the pressure drop per unit length along the channel), the pressure drop per unit length, −∆p/L, tends to approach that of the corresponding no-slip boundary case shown in Table 1. For example, in Fig. 16, −∆p/L reaches 0.59 Pa m⁻¹ when k is 10⁻¹² m² (Re = 0.5 and h = 0.001 m), which is approximately the same as the value of −∆p/L for k = 10⁻¹⁴ m² for the corresponding no-slip boundary case in Table 1. This observation is consistent with the predicted velocity profiles shown in Fig. 12, where the slip velocity is very small when k = 10⁻¹² m² and the shear stress at the interface is very close to that of the no-slip boundary case.

Figures 16 and 17 show the variation of pressure drop per unit length −∆p/L for the channel with permeable walls and varying permeability k. As the permeability k decreases, there is an increase in pressure drop per unit length −∆p/L, for all the cases shown. This again can be explained by the fact that lower permeability results in lower slip velocity at the interface and hence, a higher wall shear stress and skin friction, and the increase in skin friction consequently leads to an increase in the pressure drop, as discussed above.

It is also noticeable in Figs. 16 and 17 that, when the permeability is less than a certain threshold (and any further decrease in k will not significantly increase the pressure drop per unit length along the channel), the pressure drop per unit length −∆p/L tends to approach that of the corresponding no-slip boundary case shown in Table 1. For example, in Fig. 16, −∆p/L reaches 0.59 Pa m⁻¹ when k is 10⁻¹² m² (Re = 0.5 and h = 0.001 m), which is approximately the same as the value of −∆p/L for k = 10⁻¹⁴ m² for the corresponding no-slip boundary case in Table 1. This observation is consistent with the predicted velocity profiles shown in Fig. 12, where the slip velocity is very small when k = 10⁻¹² m² and the shear stress at the interface is very close to that of the no-slip boundary case.

3.6 Effect of Re Number on the Velocity Profiles and Pressure Drop Per Unit Length

As discussed in Sect. 3.4, the effect of Re on the velocity profiles is insignificant. This is confirmed by a further parametric study shown in Fig. 18, which shows the normalised velocity profiles of the flows with different Re ranging from 0.5 to 7, with other parameters constant at α = 1, h = 0.001 and k = 10⁻⁸ m² as shown in Fig. 12. It can be seen that the velocity profiles of flows with different Re are very similar, although there are small differences at the interface surface and in the centre line zone. As shown in the figure, the Rew numbers are different in these cases; for example, the Rew number for the Re = 0.5 case is 0.116, whereas for the Re = 5 case it is 1.25. The difference in the Rew values can be attributed to the different u_interface values as calculated by Eq. (7). Nevertheless, these differences in the normalised u_interface values are very small for the Re range studied. The same conclusion can be drawn for the other cases, suggesting that the effect of Re on the normalised velocity profiles is negligible for cases that have the same slip coefficient, channel height and wall permeability.

Fig. 18

The normalised velocity u at the interface surface with different Re numbers

The effect of Re on the pressure drops per unit length is much more pronounced as demonstrated in Figs. 10, 11, 16 and 17. The pressure drop per unit length for high Re cases (Re = 5) are an order of magnitude higher than those for the low Re(Re = 0.5) cases.

3.7 Comparison with Saffman’s Boundary Condition

At this point, it is interesting to compare the slip velocity predicted by the model (Eq. 7) and by Saffman’s boundary condition (Eq. 3). The values of ∂u/∂n derived by CFD at the fluid-porous medium interface are used in Eq. (3) to calculate u_interface, which is then compared with the analytical values of u_interface calculated by Eq. (7). Table 2 lists the normalised velocity on the interface surface calculated by both methods for different cases. Note that O(k) is neglected in Eq. (3) following Nield (2009) and Mohais et al. (2011b). The absolute values of the differences in the normalised u velocity values predicted by the two methods are less than 2% when Re = 0.5, but increase as Re increases. When Re = 7, the absolute value of the difference is as high as 5.83% for h = 0.001 m, α = 0.1 and k = 10⁻⁸ m⁻².

Table 2 Comparison of normalised velocity u at interface surface by using different equations

4 Conclusions

The flows in a 2D channel with permeable and impermeable walls were studied using CFD techniques.

The velocity profiles based on CFD were compared with analytical solutions in the literature (Potter et al. 2016) for impermeable wall conditions (no-slip boundary condition) and analytical solutions developed by Mohais et al. (2011a, b) for permeable wall conditions (slip boundary conditions). There is good agreement between the CFD results and the analytical solutions with an observed maximum difference of less than 1% for all cases investigated.

The effects of key parameters—Re, slip coefficient α, permeability k and channel height h—for the case of permeable walls were investigated using a CFD model. The results show that, in general, when the slip coefficient α decreases from 4 to 0.1, the slip velocity at the channel-porous medium interface increases, but the velocity at the channel centre decreases, leading to a ‘flatter’ velocity profile, similar to that of a plug flow. This ‘flatter’ velocity profiles are a result of lower shear stress at the interface and lower skin friction. The lower skin friction leads to lower pressure drops per unit length along the channel.

When the wall permeability k decreases, the slip velocity at the channel-porous medium interface also decreases which leads to an increase in shear stress, and hence the increase in pressure drop along the channel. As demonstrated in the results, when the permeability is less than a certain threshold, the slip velocity at the interface becomes very small and approaches to zero, and therefore the shear stress and pressure drop values approach those of the no-slip boundary cases.

The effect of Re on the velocity profiles is small for the range of Re values (0.5–7) investigated in this chapter. However, the effect of Re on the pressure drops per unit length in the channel is much more pronounced. The pressure drops per unit length for high Re cases (Re = 5) are an order of magnitude higher than those for low Re(Re = 0.5) cases.

We are developing a CFD model that includes both the channel and the porous walls to further validate the velocity solutions of Mohais et al. (2011a, b) at the channel-porous medium interfaces. The CFD model will be used to predict the pressure drops per unit length in the porous walls that is not included in the current chapter.