Keywords

1 Introduction

The fluid flow induced by periodic contraction and relaxation of the wall of the conduit carrying a fluid is termed as peristaltic transport. Naturally, peristaltic transport occurs in the flow of urine from the kidney to the bladder, chyme in the gastrointestinal tract, food bolus through the esophagus, ovum in the female fallopian tube, and blood through small blood vessels. This principle is used in industry to develop roller and finger pumps to make the flow of the fluids like foods, slurries, corrosive fluids, and blood without being contaminated due to contact with pumping machinery. First, Chakraborty [1] investigated electroosmotic augmented peristaltic transport considering thin electric double layer (EDL) where the effects of charged surface, i.e., EDL phenomenon, are assumed negligible. Later on, several researchers [2,3,4,5] made improvements in this study considering EDL effects, MHD effects, power-law fluids, and couple stress fluids. In these studies, it is concluded that peristaltic pumping can be enhanced with applied external electric field. The literature lacks with the study of electroosmotic modulated peristaltic pumping of a micropolar fluid. Micropolar fluid represents the randomly oriented particles suspended in a viscous medium. It is applicable in physiological fluids transport where the suspension of particles plays an important role like in blood (suspension of RBC, WBC, and platelets). The concept of a micropolar fluid was first presented by Eringen [6]. After that, some researchers investigated peristaltic transport of a micropolar fluid [7,8,9,10,11]. In these studies, the effects of coupling parameter and micropolar parameter on peristaltic flow characteristics are discussed.

In this paper, electroosmotic augmented peristaltic transport of a micropolar fluid via a channel with sinusoidal wave trains traveling down has been discussed. Debye-Hückel linearization is employed to simplify the problem, and electrical double layer (EDL) is considered very thin so that the effect of applied electric field is represented in terms of the electroosmotic slip velocity (i.e., Helmholtz–Smoluchowski velocity) at the channel wails. Axial velocity is achieved in the form of closed expression through low Reynolds number and long wavelength approximations.

2 Mathematical Statement of Problem

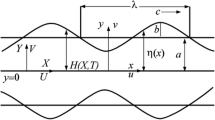
We have taken the electroosmotic augmented peristaltic transport of an incompressible micropolar fluid via a microfluidic channel of width \( 2a \). Let \( Y = {\pm} H \) be the outer and inner boundaries of the channel. The movement is thought to be incited by sinusoidal wave trains spreading through the channel dividers with a steady speed \( c \). The schematic diagram of the problem under consideration is depicted in Fig. 1 and mathematically considered as:

$$ H = a + b\sin \frac{2\pi }{\lambda }\left( {X^{\prime } - ct^{\prime } } \right), $$
(1)

where \( b \) is a wave amplitude, \( \lambda \) is a wave length, and \( t^{\prime } \) is the time. The stream is precarious in the laboratory outline \( \left( {X^{\prime } ,Y^{\prime } } \right) \), while it is consistent if seen in the coordinate system \( \left( {x^{\prime } ,y^{\prime } } \right) \), named as wave frame, moving through the wave speed \( c \). The changes between aforesaid two coordinate systems have been expressed as:

$$ x^{\prime } = X^{\prime } - ct^{\prime } ,\quad y^{\prime } = Y^{\prime } ,\quad u^{\prime } = U^{\prime } - c,\quad v^{\prime } = V^{\prime } , $$
(2)

where \( \left( {u^{\prime } ,v^{\prime } } \right) \) and \( \left( {U^{\prime } ,V^{\prime } } \right) \) are the speed segments that are considered as part of wave and laboratory frames.

Fig. 1
figure 1

Schematic diagram of physical problem

Full size image

Without body forces and the body couple, the representing conditions for the steady flow of an incompressible micropolar fluid driven by combined effects of peristaltic pumping and electroosmosis are expressed by

$$ \frac{{\partial u^{\prime } }}{{\partial x^{\prime } }} + \frac{{\partial v^{\prime } }}{{\partial y^{\prime } }} = 0, $$
(3)
$$ \rho \left( {u^{\prime } \frac{{\partial u^{\prime } }}{{\partial x^{\prime } }} + v^{\prime } \frac{{\partial u^{\prime } }}{{\partial y^{\prime } }}} \right) = - \frac{{\partial p^{\prime } }}{{\partial x^{\prime } }} + \left( {\mu + \kappa } \right)\left( {\frac{{\partial^{2} u^{\prime } }}{{\partial x^{\prime 2} }} + \frac{{\partial^{2} u^{\prime } }}{{\partial y^{\prime 2} }}} \right) + \kappa \frac{{\partial w^{\prime } }}{{\partial y^{\prime } }} + \rho_{e} E_{x} , $$
(4)
$$ \rho \left( {u^{\prime } \frac{{\partial v^{\prime } }}{{\partial x^{\prime } }} + v^{\prime } \frac{{\partial v^{\prime } }}{{\partial y^{\prime } }}} \right) = - \frac{{\partial p^{\prime } }}{{\partial y^{\prime } }} + \left( {\mu + \kappa } \right)\left( {\frac{{\partial^{2} v^{\prime } }}{{\partial x^{\prime 2} }} + \frac{{\partial^{2} v^{\prime } }}{{\partial y^{\prime 2} }}} \right) - \kappa \frac{{\partial w^{\prime } }}{{\partial x^{\prime } }}, $$
(5)
$$ \rho J^{\prime } \left( {u^{\prime } \frac{{\partial w^{\prime } }}{{\partial x^{\prime } }} + v^{\prime } \frac{{\partial w^{\prime } }}{{\partial y^{\prime } }}} \right) = - 2\kappa w^{\prime } + \gamma \left( {\frac{{\partial^{2} w^{\prime } }}{{\partial x^{\prime 2} }} + \frac{{\partial^{2} w^{\prime } }}{{\partial y^{\prime 2} }}} \right) + \kappa \left( {\frac{{\partial v^{\prime } }}{{\partial x^{\prime } }} - \frac{{\partial u^{\prime } }}{{\partial y^{\prime } }}} \right), $$
(6)

where \( u^{\prime } \) and \( v^{\prime } \) are the velocity segments in the corresponding \( x^{\prime } \) and \( y^{\prime } \) directions, \( \rho \) is the thickness of the liquid, \( p^{\prime } \) is the pressure, \( w^{\prime } \) is the microrotation speed component in the direction normal to both the \( x^{\prime } \) and \( y^{\prime } \) axes, \( J^{\prime } \) is the micro-inertia constant, \( \mu \) is the viscosity constant of the classical fluid dynamics, \( \kappa ,\gamma \) are the viscosity constants for micropolar fluid, \( E_{x} \) is the outer electric field.

For further examination, we utilize the accompanying non-dimensional factors and parameters:

$$ \begin{aligned} x & = \frac{{x^{\prime } }}{\lambda },\;\;y = \frac{{y^{\prime } }}{a},\;\;u = \frac{{u^{\prime } }}{c},\;\;v = \frac{{v^{\prime } }}{\delta c},\;\;\delta = \frac{a}{\lambda }, \\ w & = \frac{{aw^{\prime } }}{c},\;\;t = \frac{{ct^{\prime } }}{\lambda },\;\;J = \frac{{J^{\prime } }}{{a^{2} }},\;\;p = \frac{{a^{2} p^{\prime } }}{c\lambda \mu },\;\;\phi = \frac{b}{a}, \\ h & = \frac{H}{a} \\ \text{Re} & = \frac{\rho ca}{\mu } \\ \end{aligned} $$
(7)

where \( {Re} \), \( \delta \) and \( c \) represent the Reynolds number, wave number, and wave velocity, respectively. For thin EDL and weal electric field, the electrokinetic body force term may be dropped from momentum equation and it can be realized in terms of the electroosmotic slip velocity at the wall. Employing the non-dimensional variables in Eqs. (3–6) and using the low Reynolds number and long wavelength approximations, we get:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$
(8)
$$ \frac{{\partial^{2} u}}{{\partial y^{2} }} + N\frac{\partial w}{\partial y} = \left( {1 - N} \right)\frac{\partial p}{\partial x}, $$
(9)
$$ \frac{\partial p}{\partial y} = 0, $$
(10)
$$ - 2w - \frac{\partial u}{\partial y} + \left( {\frac{2 - N}{{M^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial y^{2} }} = 0, $$
(11)

where \( N = \kappa /\left( {\mu + \kappa } \right) \) is the coupling number \( \left( {0 \le N \le 1} \right) \), \( M^{2} = a^{2} \kappa \left( {2\mu + \kappa } \right)/\left( {\gamma \left( {\mu + \kappa } \right)} \right) \) is the micropolar parameter. The boundary conditions are imposed as:

$$ u\left( {x,y} \right) = U_{HS} - 1,w\left( {x,y} \right) = 0\quad {\text{at}}\,y = \pm h\left( x \right), $$
(12)
\( U_{HS} \) :

is electroosmotic slip velocity.

Solving simultaneous partial differential Eqs. (9) and (11), with boundary conditions (12), the axial velocity is obtained as:

$$ u = \left( {\frac{1 - N}{2 - N}} \right)(y^{2} - h^{2} )\frac{{{\text{d}}p}}{{{\text{d}}x}} + \frac{N}{M}\left( {\frac{1 - N}{2 - N}} \right)h\frac{{{\text{d}}p}}{{{\text{d}}x}}\frac{{\left( {\cosh Mh - \cosh My} \right)}}{\sinh Mh} + U_{HS} - 1 $$
(13)

3 Result and Discussion

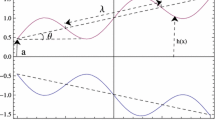
In this section, graphs are drawn showing effects of electroosmotic slip velocity and coupling number on axial velocity based on numerical results. Figure 2 shows the effect of electroosmotic slip velocity on axial velocity at \( \phi = 0.6,\,x = 1,\,{\text{d}}p/{\text{d}}x = - 5,\,M = 2,\,N = 0.1 \). From Fig. 2, it is observed that the fluid velocity enhances with the electric field applied in the flow direction but diminishes with the electric field applied against the flow direction. Figure 3 shows the variation in axial velocity with coupling number at \( \phi = 0.6,\,x = 1,\,{\text{d}}p/{\text{d}}x = - 5,\,M = 2,\,U_{HS} = 1 \). From Fig. 3, it is observed that the fluid velocity decreases with increase in coupling number.

Fig. 2
figure 2

Velocity profile at \( \phi = 0.6,\,x = 1,\,{\text{d}}p/{\text{d}}x = - 5,\,M = 2,\,N = 0.1 \) for different values of \( U_{HS} \)

Full size image
Fig. 3
figure 3

Velocity profile at \( \phi = 0.6,\,x = 1,\,{\text{d}}p/{\text{d}}x = - 5,\,M = 2,\,U_{HS} = 1 \) for different values of \( N \)

Full size image

4 Conclusion

  • The fluid velocity can be controlled by applying external electric field.

  • The fluid velocity enhances with the electric field applied in the flow direction.

  • The fluid velocity diminishes with the electric field applied against the flow direction.

The fluid velocity decreases with the increase in the coupling number.