Keywords

1 Introduction

The economic load dispatch has grown to be an essential function in process and controlling action of power system. Here, we schedule the generators that provide power by satisfying or meeting the total load demand of the system and at the same instance minimizing the cost function that is considered to be the main object function. Improvement in the economic load dispatch analysis is done in two parts.

In economic load dispatch, the cost function of various generators is in a quadratic equation form and it ignores the transmission network limitations [1]. There are basically two constraints in economic load dispatch problem. First one is equality constraint, and second is inequality constraint. The real and reactive power of generator limits is also varied in the specified limits to minimize the fuel cost. Equality constraint is basically used for load generation balance [2]. Inequality constraint consists of voltage constraint and generator constraint. Voltage constraint describes about the voltage limits within which we need to transfer the power, and generator constraint describes the KVA loading of generator should not exceed the prescribed limits. In power system, all the various power plants including the generating units are located at a very large distance from the load demand centres, and huge amount of economy gets varied due to the losses, generation cost, fuel cost, maintenance cost, transmission cost, etc., and therefore, to maintain the stability of the system, proper scheduling of the generating units is very essential part of power system.

The various nature-inspired optimization techniques are real-coded genetic algorithm [3], genetic algorithm [4] particle swarm optimization [5], new particle swarm optimization [6], differential evolution [7], recent advances in economic dispatch [8], quantum-inspired particle swarm optimization [9], simulated annealing [10], biogeography-based optimization [11], artificial immune system [12], evolutionary programming optimization for solving economic load dispatch problems of power system [13], artificial bee colony algorithm [14] and improved differential evolution [15].

The modern optimization technique used in this paper is the moth flame optimization algorithm. This algorithm is used to minimize the objective function by satisfying various constraints of the system so as to provide the effective results. It is a novel nature-inspired optimization paradigm. The most effective technique or the methodology of this optimization is the tendency of the navigation of the fanciest insects called moths in nature. This navigation tendency is referred as the transverse orientation. By keeping this methodology, various results have been calculated to make the system more efficient.

2 Problem Formulation

The primary objective of economic load dispatch problem is to meet the load demand of power system by minimizing the objective function which is the cost function equation of various generating units. This cost function is represented mathematically in quadratic form having various cost coefficients and variables. The amount of power generated from these generating units is shown by \( P_{i} \) MW.

Where:

  • \( i = \) number of generating units of the power system network whose values are ranging from 1 to n.

  • \( F_{i} = \) fuel cost of ith generating unit.

  • \( P_{i} = \) power generated from the ith generating unit.

  • \( F_{i} \left( {P_{i} } \right) = \) cost function of ith generating unit in power system.

  • \( a_{i} , \, b_{i} \, \text{and} \, c_{i} \) are the fuel cost coefficients of the ith generating unit.

  • \( P_{D} = \) total power demand of the system.

  • \( P_{L} = \) total power loss occurred in the system.

  • \( V_{\min} = \) minimum value of the voltage.

  • \( V_{\max} = \) maximum value of the voltage.

  • \( P_{i}^{\min} = \) minimum value of the power generated by the ith generating unit.

  • \( P_{i}^{\max} = \) maximum value of the power generated by the ith generating unit.

The objective function which is a cost function equation is represented as follows:

$$ \text{Min}\,F_{i} \left( {P_{i} } \right) = \hbox{min} \mathop \sum \limits_{i = 1}^{n} \left[ {\left( {a_{i} \times P_{i}^{2} + b_{i} \times P_{i} + c_{i} } \right)} \right] $$

This equation is a convex type economic load dispatch problem formulation. The economic dispatch for a certain load demand should also satisfy the following constraints.

  1. (A)

    Equality Constraint:

  1. (1)

    Power Balance Constraint:

If the losses are considered, the equation is:

$$ \mathop \sum\limits_{i = 1}^{n} P_{i} = P_{D} + P_{L} $$

In this system, the losses are zero; therefore, the power balance constraint equation becomes as follows:

$$ \mathop \sum\limits_{i = 1}^{n} P_{i} = P_{D} $$
  1. (B)

    Inequality constraints:

  1. (1)

    Voltage Constraint: It describes about the voltage limits within which we need to transfer our power to the load.

    $$ V_{\min} \le V \le V_{\max} $$
  2. 2.

    Generator Constraint: It describes the KVA loading of the generator should not exceed the limits.

    $$ P_{i}^{\min} \le P \le P_{i}^{\max} $$

3 Moth Flame Optimization Algorithm

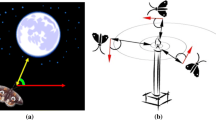
This algorithm has completely adopted a special way of navigational technique adopted by the insects called as moths, and hence, this enhances its feature in this modern research system.

The moths have a tendency of flying in night by maintaining a constant angle with respect to moon. This makes them to travel in a straight line. If there is any artificial light, then they move spirally. Hence, this special movement technique is used in the optimization process.

Steps for the proposed algorithm are as follows:

  1. 1.

    Initially, we assume the total population of moths. We randomly generate the initial positions of moths in the space. The moths have a tendency of moving around the flame in a specific manner.

    $$ A\left( {k,l} \right) = \left( {\text{popmax} \left( k \right)-\text{popmin} \left( k \right)} \right)* \text{rand} \left( \, \right) + \text{popmin} \left( k \right); $$

    Here, \( \text{popmax} \) is the maximum limit of the power generated by the generator, and \( \text{popmin} \) is the minimum limit of the power generated by the generator.

  2. 2.

    After the generation of initial positions of moths, this function runs till this condition is satisfied.

  3. 3.

    After every iteration, the sorting of flames is done. Therefore, we update the number of flames by using formula as:

    $$ \text{flame number} = \text{round}\left( {S{-}R * \frac{S - 1}{V}} \right) $$

    where \( S \) is the maximum number of flames, \( R \) is the number of iterations, and \( V \) is the maximum number of iterations. After each execution of the iterations, the sequence of the flames changes and moths update their position with respect to the flame.

  4. 4.

    The condition is checked whether the moths are within the searching area or not. If the moths are within the searching area, it is called as exploitation, and if the moths are outside the range of searching area, it is called as exploration. If moths are not within the area, then they are needed to bring back.

  5. 5.

    Now, the iteration condition is satisfied. If the condition gets satisfied, the sorting of the population of moths is done. It updates the new position of moths in the searching area.

  6. 6.

    For every iteration, the condition is checked that whether the moths are lesser than or equal to the flame number, and if the condition is satisfied, then the flames are sorted according to their fitness values. Then, we update the new positions of moths with respect to the corresponding flame.

  7. 7.

    Now, the process of updating a new positions of moths with respect to the flames after every iteration is done by following a special function called as spiral function. In this algorithm, this spiral movement is considered as very essential function which also gives about the assurance of the exploitation concept which means that moth always lies within the searching area of the region. The equation for spiral function is defined as

    $$ P\left( {A_{k} ,B_{l} } \right) = H_{k} \cdot \text{e}^{gt} \cos \left( {2\varPi \cdot t} \right) + B_{l} $$

    where \( H_{k} \) represents the distance of kth moth from the lth flame, \( g \) is defined as the constant for the shape of the spiral function, and \( t \) is the random number in \( \left[ {1, - 1} \right]. \)

  8. 8.

    After assigning moths to new position, we need to calculate the distance of moth from the flame using the following equation:

    $$ H_{k} = \left| {B_{l} - A_{k} } \right| $$

    where \( H_{k} \) is the distance of kth moth, \( B_{l} \) indicates the lth flame, and \( A_{k} \) is the kth moth.

  9. 9.

    Now to calculate \( t \), we are considering a constant \( q \) called as the convergence constant whose value decreases from \( - 1 \) to \( - 2 \) over the entire process of iteration. Here, the convergence curve defines the best flame score. This factor results a fast convergence of moths around the flame during the entire iteration process.

The proposed nature-inspired moth flame optimization technique has been worked in the MATLAB software. The accuracy and the efficiency of the algorithm have been tested in two systems to resolve the economic load dispatch dilemma by optimizing the object function. The optimization is made without bearing in mind the power losses.

4 Results Discussion

This case studies an 18 unit thermal generating system for optimization process. The input information for standard 18 unit system is occupied from the reference [3]. The system data includes the values of the constant coefficients in the total fuel cost equation of the generating units without any power losses. The maximum power demand for this system is \( 365\,\text{MW} \), and the various percentages factor considered are 80 and 70% of the maximum power demand. The obtained results are shown in the Table 1 which validates and proofs the effective performance and accuracy of the MFO algorithm, and its results are compared with those obtained from the biogeography-based optimization (BBO) [11], real genetic algorithm (RGA) and lambda iteration. Figs. 1 and 2 shows the power generated by all the 18 generating units whose summation of the values becomes equal to the power demanded.

Table 1 Comparison results for 18 unit system (maximum power P = 365 MW)
Full size table
Fig. 1
figure 1

Cost convergence characteristics curve for power demand \( P_{D} = 255.5 \,\text{MW} \)

Full size image
Fig. 2
figure 2

Cost convergence characteristics for power demand \( P_{D} = 292\,\text{MW} \)

Full size image

Table 1 gives us a brief description about the comparison results obtained from the proposed moth flame optimization technique with those of earlier results obtained from the biogeography-based optimization algorithm, real genetic algorithm, genetic algorithm and λ iterations. The new results gained have much more accuracy and effectiveness in solving the problems of economic load dispatch concept.

5 Conclusion

This paper effectively validates the proposed MFO algorithm to solve ELD problems of power system by obtaining the better results as compared to other implemented techniques in previous analysis. The main purpose of optimizing the ELD problems has been done to minimize the cost function of the generating units, and hence, lesser value of cost is obtained with the proposed technique as nowadays the cost reduction has become a vast area of interest in solving the ELD problems. Therefore, this concept extremely requires a very effective strategy in proper planning and controlling of the generating units in the power plant. Comparing and considering the various previous obtained results, various convergence characteristics, demands and with the new obtained results, it can be inferred that the proposed methodology performs very effectively, having great potential in solving the problems, having faster solution obtaining capability and has feasibility in nature, and hence, it can be concluded that the proposed methodology can be applied for optimizing the ELD problems in the power system.