Abstract
In this paper, we consider an eco-epidemiological model with Holling type III functional response and a time delay representing the gestation period of the predator. In the model, it is assumed that the predator population suffers a transmissible disease. By means of Lyapunov functionals and Laselle’s invariance principle, sufficient conditions are obtained for the global stability of the endemic coexistence of the system.
This work was supported by the National Natural Science Foundation of China (No. 11371368) and the Natural Science Foundation of Hebei Province (No. A2014506015).
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Epidemiological models have received considerate attention in the literature to explain the spread and control of infectious disease [1,2,3,4]. Most of these models descend from the pioneering work of Kermack and Mckendrick [5], who proposed the classical SIR model . Seeing that species do not exist alone in the nature world, so it is very important to study the system of two or more interacting species subjected to disease [6].
Recently, great attention has been paid to study the relationships between demographic processes among different populations and diseases (see, e.g., [7,8,9,10,11]). Such as, Zhang et al. [7] studied the following eco-epidemiological model with Holling type I response function
where x(t), S(t), I(t) denote the densities of the prey, the susceptible predator, and the infected predator population, respectively.
In system (1.1), it assumes that the per capita rate of predation depends on the prey numbers only. But Holling found that each predator increased its consumption rate when exposed to a higher prey density, and also predator density increased with increasing prey density [12, 13]. So he suggested the following three kinds of functional responses referring to the number of prey eaten per predator per unit time.
where x denotes the density of prey, \(a>0\) is the search rate of the predator, \(m>0\) is half-saturation constant, \(p_1(x)\), \(p_2(x)\), and \(p_3(x)\) represent Holling type I, II, and III functional responses, respectively.
Holling type III functional response reveals that the risk of being preyed upon is small at low prey density but increases up to a certain point as prey density increases, which is in accordance with some phenomena of natural world. Also, we know that many factors contribute to a type III functional response such as prey refuge, predator learning, and the presence of alternative prey [14].
Motivated by the works of Holling [14] and Zhang et al. [7], in this paper, we consider a delayed eco-epidemiological model with Holling type III functional response, which suffers a transmissible disease. Thus, we study the following eco-epidemiological model:
where x(t), S(t), and I(t) represent the densities of the prey, the susceptible predator, and the infected predator population, respectively. r is the intrinsic growth rate of prey population without disease, \(r/a_{11}\) is the environmental carrying capacity, \(a_{12}\) is the capturing rate of the susceptible predators. The infected predator also can catch the prey; here, \(a_{13}\) denotes the capturing rate of the infected predator. k is the conversion rate of nutrients into the reproduction of predators by consuming prey, \(\beta \) is the disease transmission coefficient, \(r_1\) is the natural death rate of the susceptible predators, \(r_2\) is the natural and disease-related mortality rate of the infected predator. Here, \(r_1<r_2\). \(\tau \) is a time delay representing a duration of \(\tau \) time units elapses when an individual prey is killed and the moment when the corresponding addition is made to the predator population. All the parameters are positive.
The initial conditions for system (1.2) are
where \(R_+^3={(x_1,x_2,x_3):x_1\ge 0 ,x_2\ge 0,x_3\ge 0}.\)
The organization of this paper is as follows. In Sect. 2, the positivity and the equilibria of system (1.2) are presented. In Sect. 3, we consider about the permanence of system (1.2) by using the persistence theory on infinite dimensional systems developed by Hale and Waltman [15]. In Sect. 4, we establish sufficient conditions for the global asymptotic stability of the endemic-coexistence equilibrium of system (1.2) by constructing suitable Lyapunov functionals and adopting Lasalle’s invariance principle. Finally, we discuss the biological meaning of the result obtained in this paper.
2 Preliminaries
In this section, we consider the positivity of solutions and the equilibria of system (1.2).
2.1 Positivity of Solutions
Theorem 2.1
Suppose that (x(t), S(t), I(t)) is a solution of system (1.2) with initial conditions (1.3). Then, \(x(t)\ge 0\), \(S(t)\ge 0\), and \(I(t)\ge 0\) for all \(t\ge 0\).
Proof
From the first equation of system (1.2), we have
Hence, x(t) is positive.
In order to prove that S(t) is positive on \([0,\infty ]\), suppose that there exists \(t_1>0\) such that \(S(t_1)=0\), and \(S(t)>0\) for \(t\in [0,t_1]\). Then, \(\dot{S}(t_1)\le 0\). From the second equation of (1.2), we have
which is a contradiction.
In order to show that I(t) is positive on \([0,\infty ]\), suppose that there exists \(t_2>0\) such that \(I(t_2)=0\), and \(I(t)>0\) for \(t\in [0,t_2]\). Then, \(\dot{I}(t_2)\le 0\). From the third equation of (1.2), we have
which is a contradiction. \(\square \)
2.2 Equilibria
System (1.2) possesses the following equilibria in general.
-
(i)
The trivial equilibrium \(E_{0}=(0,0,0)\).
-
(ii)
The predator-extinction equilibrium \(E_{1}=(r/a_{11},0,0)\).
-
(iii)
The disease-free equilibrium \(E_{2}=(x_{2},S_{2},0)\), where
$$\begin{aligned} \begin{aligned} x_{2}&=\sqrt{\dfrac{r_1}{ka_{12}-r_1m}},\\ S_2&=\dfrac{k}{\sqrt{r_1(ka_{12}-r_1m)}} \left( r-a_{11}\sqrt{\dfrac{r_1}{ka_{12}-r_1m}}\right) .\\ \end{aligned} \end{aligned}$$(2.1)We denote an ecological threshold parameter by \(\mathfrak {R}_1=\dfrac{k}{r_1}\dfrac{r^2a_{12}}{a_{11}^2+mr^2}\). It is easy to show that if \(\mathfrak {R}_1>1\), then \(x_2>0,\) \(I_2>0.\)
-
(iv)
The planar equilibrium \(E_{3}=(x_{3},0,I_{3})\), where
$$\begin{aligned} \begin{aligned} x_{3}&=\sqrt{\dfrac{r_2}{ka_{13}-r_2m}},\\ I_3&=\dfrac{k}{\sqrt{r_2(ka_{13}-r_2m)}} \left( r-a_{11}\sqrt{\dfrac{r_2}{ka_{13}-r_2m}}\right) .\\ \end{aligned} \end{aligned}$$(2.2)Similar, we denote \(\mathfrak {R}_2=\dfrac{k}{r_2}\dfrac{r^2a_{13}}{a_{11}^2+mr^2}\). It is easy to show that if \(\mathfrak {R}_2>1\), then \(x_3>0,\) \(I_3>0.\)
-
(v)
The endemic-coexistence equilibrium \(E^{*}=(x^{*},S^{*},I^{*})\), where
$$\begin{aligned} \begin{aligned} I^{*}=&\dfrac{ka_{12}x^{*2}}{\beta (1+mx^{*2})}-\dfrac{r_1}{\beta },\\ S^{*}=&\dfrac{r_2}{\beta }-\dfrac{ka_{13}x^{*2}}{\beta (1+mx^{*2})}, \end{aligned} \end{aligned}$$(2.3)in which \(x^*\) is a positive real root of the following cubic equation:
$$\begin{aligned} m\beta a_{11}x^3-mr\beta x^2+(a_{11}\beta +r_2a_{12}-a_{13}r_1)x-r\beta =0. \end{aligned}$$(2.4)
It can be seen that if
-
(H1)
\(r_2(ka_{12}-r_1m)>r_1(ka_{13}-r_2m),\)
then system (1.2) has a endemic-coexistence equilibrium \(E^{*}\).
3 Permanence
In this section, we study the permanence of system (1.2). Before starting our theorem, we give some basic concepts and corresponding theory.
Definition 3.1
System (1.2) is said to be permanent (uniformly persistent) if there are positive \(m_{i}\) and \(M_{i}(i=1,2,3)\) such that each positive solution (x(t), S(t), I(t)) of system (1.2) satisfies
Definition 3.2
System (1.2) is said to be permanent if there exists a compact region \(\Omega _0\in \texttt {int}\Omega \) such that every solution of Eqs. (1.2) with initial condition (1.3) will eventually enter and remain in region \(\Omega _0\).
It is easy to see that for a dissipative system, uniform persistence is equivalent to permanence. For the sake of convenience, we present the uniform persistence theory for infinite dimensional systems.
Let X be a complete metric space with metric \(\mathrm {d}\). Suppose that T is a continuous semiflow on X, that is, a continuous mapping \(T:[0,+\infty ]\times X\rightarrow X\) with the following properties
where \(T_t\) denotes the mapping from X to X given by \(T_t(x)=T(t,x)\).
The distance \(\mathrm {d}(x,Y)\) of a point \(x\in X\) from a subset Y of X is defined by
Recall that the positive orbit \(\gamma ^+(x)\) through x is defined as \(\gamma ^+(x)=\cup _{t\ge 0}\{T(t)x\},\) and its \(\omega -\) limit set is \(\omega (x)=\cap _{s\ge 0}\overline{\cup _{t\ge s}\{T(t)x\}}\). Define \(W^s(A)\) the strong stable set of a compact invariant set A as
Suppose that \(X^0\) is open and dense in X and \(X^0\cup X_0=X\), \(X^0\cap X_0=\emptyset \). Moreover, the \(C^0\)-semigroup T(t) on X satisfies
Let \(T_b(t)=T(t)\mid _{X_0}\) and \(A_b\) be the global attractor for \(T_b(t)\).
Lemma 3.1
(Hale and Waltman [15]) Suppose that T(t) satisfies (3.1). If the following hold
-
(i)
there is a \(t_0\ge 0\) such that T(t) is compact for \(t>t_0\);
-
(ii)
T(t) is point dissipative in X; and
-
(iii)
\(\bar{A}_b=\cup _{x\in A_b}\omega (x)\) is isolated and has an acyclic covering \(\hat{M}_t\), where
$$\begin{aligned} \hat{M}_t=\{\tilde{M}_1,\tilde{M}_2,\ldots ,\tilde{M}_n\}; \end{aligned}$$ -
(iv)
\(W^s(\tilde{M}_i)\cap X^0=\emptyset \) for \(i=1,2,\ldots ,n.\)
Then, \(X_0\) is a uniform repeller with respect to \(X^0\); that is, there is an \(\varepsilon >0\) such that for any \(x\in X^0\), \(\liminf _{t\rightarrow +\infty }\mathrm {d}(T(t)x,X_0)\ge \varepsilon \).
We also need the following result to study the permanence of system (1.2).
Lemma 3.2
There are positive constants \(M_1\) and \(M_2\) such that for any positive solution (x(t), S(t), I(t)) of system (1.2) with initial conditions (1.3),
Proof
Let (x(t), S(t), I(t)) be any solution of system (1.2) with initial conditions (1.3). Consider the function
\(V(t)=kx(t)+S(t+\tau )+I(t+\tau ).\)
From system (1.2), we get
where \(M_1=\dfrac{k(r+r_1)^2}{4a_{11}}\). Which yields \(\limsup _{t\rightarrow +\infty } V(t)\le M_1\). If we choose \(M_2=M_1/k,\) then (3.2) follows. This complete the proof. \(\square \)
In the following, we investigate the permanence of system (1.2).
Theorem 3.1
If \(\beta S_2>r_2\) holds, then system (1.2) is permanent.
Proof
Let \(C^+([-\tau ,0],\mathbb {R}_+^3)\) denote the space of continuous functions mapping \([-\tau ,0]\) into \(\mathbb {R}_+^3\). Define
Denote \(C_0=C_1\cup C_2\), \(X=C^+([-\tau ,0],\mathbb {R}_+^3)\), and \(C^0=\text {int}C^+([-\tau ,0],\mathbb {R}_+^3)\).
We verify below that the conditions in Lemma 3.1 are satisfied. By the definition of \(C^0\) and \(C_0\), it is easy to know that \(C^0\) and \(C_0\) are positively invariant. Moreover, the conditions (i) and (ii) in Lemma 3.1 are clearly satisfied. Thus, we need only to verify that the conditions (iii) and (iv) hold. System (1.2) has two constant solutions in \(C_0\) : \(\bar{E}_1\in C_1\), \(\bar{E}_2\in C_2\) corresponding, respectively, to \(x(t)=r/a_{11}\), \(S(t)=0,\) \(I(t)=0\) and \(x(t)=x_2\), \(S(t)=S_2\), \(I(t)=0\).
Firstly, we verify the condition (iii) of Lemma 3.1. If (x(t), S(t), I(t)) is a solution of system (1.2) initiating from \(C_1\), then \(\dot{x}(t)=rx(t)-a_{11}x^2(t)\), which yields \(x(t)\rightarrow r/a_{11}\) as \(t\rightarrow +\infty \). If (x(t), S(t), I(t)) is a solution of system (1.2) initiating from \(C_2\) with \(\phi _1(\theta )>0\) and \(\phi _2(\theta )>0\), then we have
It is obvious that if \(\beta S_2/r_2>1\), then \(\mathfrak {R}_1>1\). Using Lemmas 3.1 and 3.2, it is easy to prove that if \(\mathfrak {R}_1>1\) holds, then system (3.3) is uniformly persistent. Noting that \(C_1\cap C_2=\emptyset \), this shows that the invariant sets \(\bar{E}_1\) and \(\bar{E}_2\) are isolated. Hence, \(\left\{ \bar{E}_1,\bar{E}_2\right\} \) is isolated and is an acyclic covering.
Secondly, we show that \(W^s(\tilde{E}_i)\bigcap C^0=\emptyset (i=1,2)\). Here, we restrict out attention to show \(W^s(\tilde{E}_2)\bigcap C^0=\emptyset \) holds because the proof of \(W^s(\tilde{E}_1)\bigcap C^0=\emptyset \) is simple. Assuming the contrary, namely \(W^s(\tilde{E}_2)\bigcap C^0\ne \emptyset \). Then, there exists a positive solution (x(t), S(t), I(t)) satisfying \(\lim _{t\rightarrow +\infty }(x(t),S(t),I(t))=(x_2,S_2,0)\).
Since \(\beta S_2>r_2\), we can choose \(\varepsilon >0\) small enough such that
Noting that \(\lim _{t\rightarrow +\infty }S(t)=S_2\), for \(\varepsilon >0\) sufficiently small satisfying (3.3), there is a \(t_0>0\) such that if \(t>t_0\), \(S_2-\varepsilon<S(t)<S_2+\varepsilon \). For \(\varepsilon >0\) sufficiently small satisfying (3.4), it follows from the third equation of system (1.2) that for \(t>t_0+\tau \), \(\dot{I}(t)>\beta (S_2-\varepsilon )I(t)-r_2I(t)\), which, follows from (3.4), yields \(\lim _{t\rightarrow +\infty }I(t)=+\infty .\) This is contradicts Lemma 3.2. Thus, we have \(W^s(\tilde{E}_2)\bigcap C^0=\emptyset \). By Lemma 3.1, we conclude that \(C_0\) repels positive solutions of system (1.2) uniformly, and therefore, system (1.2) is permanent. The proof is complete. \(\square \)
4 Global Stability
Theorem 4.1
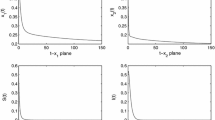
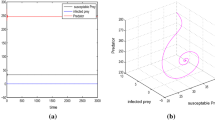
If the endemic-coexistence equilibrium \(E^*\) of system (1.2) exists, then \(E^*\) is globally asymptotically stable provided that
(H2): \(\underline{x}\ge r/(2a_{11})\).
Here, \(\underline{x}\) is the persistency constant for x satisfying \(\liminf _{t\rightarrow +\infty }x\ge \underline{x}\).
Proof
Assume that (x(t), S(t), I(t)) is any positive solution of system (1.2) with initial conditions (1.3). Denote \(\phi (x(t))=\dfrac{x^2(t)}{1+mx^2(t)}\). Define
Calculating the derivative of \(V_{11}(t)\) along positive solutions of system (1.2), it follows that
On substituting \(rx^*-a_{11}x^{*2}-a_{12}\phi (x^*)S^*-a_{13}\phi (x^*)I^{*}=0\), \(ka_{12}\phi (x^*)S^* -r_1S^*-\beta S^*I^{*}=0\), and \(\beta S^*I^{*}+ka_{13}\phi (x^*)I^{*}-r_2 I^{*}=0\) into Eq. (4.2), we derive that
Define
Then,
Set \(V_1(t)=V_{11}(t)+V_{12}(t)+V_{13}(t)\). It follows from (4.1) (4.4), and (4.5) that
Noting that
we derive from (4.7) that
On substituting \(ka_{12}\phi (x^*) =r_1+\beta I^{*}\) and \(ka_{13}\phi (x^*)=r_2-\beta S^*\) into Eq. (4.8), we derive that
Noting that \(\phi (x^*)=\dfrac{x^{*2}(t)}{1+mx^{*2}(t)}\) and \(\phi (x)=\dfrac{x^{2}(t)}{1+mx^{2}(t)}\), we derive from (4.9) that
Since (H2) holds, there exists a constant \(T>0\) such that if \(t\ge T\), \(x(t)>r/(2a_{11}).\) In this case, we have that, for \(t\ge T\),
with equality if and only if \(x=x^*\). Seeing that the function \(f(x)=x-1-\ln x\) is always nonnegative for any \(x>0\), and \(f(x)=0\) if and only if \(x=1\), therefor, if \(t\ge T\), \(\dot{V}_1(t)\le 0,\) which equality if and only if \(x=x^*\), \(S(t)=S(t-\tau ),\) \(I(t)=I(t-\tau ).\) We now look for the invariant subset M within the set
Since \(x=x^*,\) \(S(t)=S(t-\tau )\), \(I(t)=I(t-\tau )\) on M, it follows from the system (1.2) that
which yields \(S=S^*\) and \(I=I^{*}\). Hence, the only invariant set in M is \(\mathbb {M}={(x^*,S^*,I^{*})}\). Therefore, the global asymptotic stability of \(E^*\) follows from Lasalle’s invariance principle for delay differential systems [16]. This completes the proof. \(\square \)
5 Discussion
In this paper, we have proposed and analyzed an eco-epidemiological system with time delay due to the gestation of the predator. We assumed that a transmissible disease spreading among the predator population, meanwhile, both the susceptible predator and the infected predator can catch the prey. Specially, system (1.2) has no intraspecific competition terms in the second and the third equations. In this case, under what conditions will the global stability of a feasible equilibrium of system (1.2) persists independent of the time delay? We established global asymptotic stability of the endemic-coexistence equilibrium of the system by means of Lyapunov functionals and Laselle’s invariance principle. According to Theorem 4.1, we can see that the endemic-coexistence equilibrium of system (1.2) is globally asymptotically stable when the prey population is abundant enough.
References
Beretta, E., Hara, T., Ma, W., Takeuchi, Y.: Global asymptotic stability of an SIR epidemic model with distributed time delay. Nonlinear Anal. 47, 4017–4115 (2001)
Gakkhar, S., Negi, K.: Pulse vaccination in SIRS epidemic model with non-monotonic incidence rate. Chaos Solitions Fractals 35, 626–638 (2008)
Xu, R., Ma, Z.E., Wang, Z.P.: Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity. Comput. Math. Appl. 59, 3211–3221 (2010)
Xu, R.: Global dynamics of an SEIRI epidemioligical model with time delay. Appl. Math. Comput. 232, 436–444 (2014)
Kermack, W.Q., Mckendrick, A.G.: Contributions to the mathematical theory of epidemics (Part I). Proc. R. Soc. A 115, 700–721 (1927)
Anderson, R.M., May, R.M.: Regulation stability of host-parasite population interactions: I. Regulatory processes. J. Anim. Ecol. 47, 219–267 (1978)
Zhang, J., Li, W., Yan, X.: Hopf bifurcation and stability of periodic solutions in a delayed eco-epidemiological system. Appl. Math. Comput. 198, 865–876 (2008)
Debasis, M.: Hopf bifurcation in an eco-epidemic model. Appl. Math. Comput. 217, 2118–2124 (2010)
Bairagi, N.: Direction and stability of bifurcating periodic solution in a delay-induced eco-epidemiological system. Int. J. Differ. Equ. 1–25 (2011)
Xu, R., Tian, X.H.: Global dynamics of a delayed eco-epidemiological model with Holling type-III functional response. Math. Method Appl. Sci. 37, 2120–2134 (2014)
Sahoo, B.: Role of additional food in eco-epidemiological system with disease in the prey. Appl. Math. Comput. 259, 61–79 (2015)
Holling, C.S.: The components of predation as revealed by a study of small mammal predation of the European pine sawfly. Can. Entomol. 91, 293–320 (1959)
Holling, C.S.: Some characteristics of simple types of predation and parasitism. Can. Entomol. 91, 385–398 (1959)
Holling, C.S.: The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 45, 3–60 (1965)
Hale, J., Waltman, P.: Persistence in infinite-dimensional systems. SIAM J. Math. Anal. 20, 383–395 (1989)
Haddock, J.R., Terjéki, J.: Liapunov-Razumikhin functions and an invariance principle for functional-differential equations. J. Differ. equ. 48, 95–122 (1983)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Bai, H., Xu, R. (2018). Global Stability of a Delayed Eco-Epidemiological Model with Holling Type III Functional Response. In: Kar, S., Maulik, U., Li, X. (eds) Operations Research and Optimization. FOTA 2016. Springer Proceedings in Mathematics & Statistics, vol 225. Springer, Singapore. https://doi.org/10.1007/978-981-10-7814-9_9
Download citation
DOI: https://doi.org/10.1007/978-981-10-7814-9_9
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-7813-2
Online ISBN: 978-981-10-7814-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)