Synthesis of Linear Antenna Array Using Cuckoo Search and Accelerated Particle Swarm Algorithms

Abstract

Array pattern synthesis has a lot of importance in most of the communication and radar systems. It increases in defining the appropriate configuration of the array, which produces desired radiation pattern. Low sidelobe narrow beams are very useful for point-to-point communication and high-resolution radars. In this chapter, two evolutionary computing techniques like cuckoo search algorithm and accelerated particle swarm optimization are used. The desired amplitude levels are achieved by the algorithm with element spacing d = 0.40 and 0.45. The main objective is to generate patterns with fixed beam width with acceptable sidelobe level. The results are compared with conventional Taylor method. The array patterns are numerically computed for 100 number of elements.

1 Introduction

Array antennas have a great importance because its radiators have the ability to exhibit beam scanning with enhanced gain and directivity [1]. For a desired pattern, appropriate weighting vector is used. The major advantages of the use of array are that the mainlobe direction and sidelobe level of radiation pattern are controllable and function of the magnitude and the phase of the excitation current and the position of each array element [2].

Various analytical and numerical techniques have been developed to meet this challenge [3]. Analytical techniques converge to local values rather than global optimum values, which optimize further when compared to mathematical techniques [4]. Hence, there is need of evolutionary techniques so we can achieve the desired patterns with minimum sidelobe level [5].

The most used optimization techniques in array pattern synthesis are steepest descent algorithms. In this chapter, an effective method based on Cuckoo Search Optimization [6] (CSA) and Accelerated Particle Swarm Optimization [7] (APSO) is proposed for synthesizing of linear antenna array. As an excellent search and optimization algorithm, CSA has gained more and more attention and has very wide applications.

In this chapter, a CSA and APSO are applied for array synthesis, to control the desired pattern, for linear geometrical configuration with various spacing ranging between 0.40 λ and 0.45 λ relative displacement between the elements, the excitation amplitudes of individual elements and with no additional phase are computed.

2 Array Formulation and Fitness Calculation

2.1 Linear Array

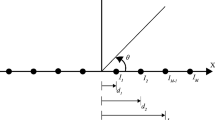
Because of its simple design, most commonly a linear array is synthesized for many communication problems [8]. The representation of such geometry is as shown in Fig. 1. Considering a linear array of N isotropic antennas, where all the antenna elements are identically spaced at a distance d from one another along the x-axis [9].

Fig. 1

Linear array antenna

The free space far-field pattern E (u) is given by

$$ {\text{E}}\left( {\text{U}} \right) = 2\sum\limits_{{{\text{n}} = 0}}^{\text{N}} {{\text{A}}_{\text{n }} { \cos }\left[ {{\text{k}}\left( {{\text{n}} - 0.5) {\text{d}}({\text{u}} - {\text{u}}_{\text{o}} } \right)} \right]} $$

(1)

where

${\text{A}}_{\text{n }}$ :

excitation of the nth element on either side of the array

K:

wave number = 2π/λ

λ:

wavelength

θ:

angle between the line of observer and broadside

$\uptheta_{0}$ :

Scan angle

d:

spacing between the radiating elements

u:

sin θ

u₀ :

sin θ₀

Normalized far field in dB is given as

$$ {\text{E}}\left( {\text{U}} \right) = 20{ \log }_{10 } \frac{{\left| {{\text{E}}\left( {\text{U}} \right)} \right|}}{{\left| {{\text{E}}\left( {\text{U}} \right)_{ \hbox{max} } } \right|}} $$

(2)

The excitation amplitudes are taken as parameters to be optimized with the objective of achieving reduced sidelobe level. Equation (1) is used to find the far-field pattern information of current amplitude excitation ${\text{A}}_{\text{n }}$ for all the elements, with element spacing as d = (0.40 and 0.45) with zero additional phase.

In this optimization process, a design is made to minimize the sidelobe level of the radiation pattern without disturbing the gain of the main beam. The problem of minimizing the maximum SLL in the pattern with prescribed beamwidth by varying wavelength spaced array is solved using the fitness function. An appropriate set of element amplitudes are achieved by reduced sidelobe levels.

Thus, the fitness function is formulated as

$$ \begin{aligned} {\text{Fitness}} = {\text{Obtained}}\,{\text{Peak}}\,{\text{SLL}} & \, - \,{\text{Desired}}\,{\text{Peak}}\,{\text{Side}}\,{\text{SLL}} \\ & - 1 \le {\text{u}} \le 1 \;{\text{u}} \ne {\text{u}}_{0} \\ \end{aligned} $$

$$ \begin{array}{*{20}l} {{\text{Here}}\,{\text{Obtained}}\,{\text{Peak}}\,{\text{SLL}} = { \hbox{max} }[20\log_{10 } \frac{{\left| {{\text{E}}\left( {\text{U}} \right)} \right|}}{{\left| {{\text{E}}\left( {u_{0} } \right)_{max} } \right|}}]} \hfill \\ {{\text{Desired}}\,{\text{Peak}}\,{\text{SLL}} = - 35\,\,{\text{dB}}} \hfill \\ \end{array} $$

3 Optimization Techniques

3.1 Cuckoo Search Algorithm (CSA)

The CSA mimics the natural behavior of cuckoo birds [10]. The principle depends on reproduction strategy of cuckoos. The algorithm has 3 idealized assumptions:

• 1. Egg laid by a cuckoo in a specific time is reserved for hatching.

• 2. Depending on the nest, the quality of the egg is defined.

• 3. Host nests are finite and the probability of identifying eggs lies between (0 and 1).

Random-walk style search is implemented by by Lévy flights [11]. Single parameter in Cuckoo Search Algorithm makes it simpler when comparing the other agent-based metaheuristic algorithms. The new generation of excitation current amplitude are determined by the best nest. The updating procedure is mentioned in the following Eq. (3)

$$ {\text{X}}_{\text{i}}^{{\left( {{\text{t}} + 1} \right)}} = {\text{X}}_{\text{i}}^{{\left( {\text{t}} \right)}} +\upalpha \,\oplus \,{\text{L}}{\acute{\text{e}}}{\text{vy}}(\uplambda), $$

(3)

The Levi flight equation represents the stochastic equation for random-walk as it depends on the current position and the transition probability (second term in the equation). Where α is the step size, generally α = 1. Element wise multiplications is given as:

$$ {\text{L}}{\acute{\text{e}}} {\text{vy}}\sim{\text{u}} = {\text{t}}^{{ -\uplambda}} ,\quad \left( {1 <\uplambda \le \text{3}} \right) . $$

(4)

Here, the term t^−λ refers to the fractal dimension of the step size and the probability Pa in this paper is taken as 0.25 [12].

3.2 Accelerated Particle Swarm Optimization

The standard PSO uses both the individual personal best and the current global best but APSO uses global best only [13]. This technique interestingly accelerates the search efficiency and iteration time.

It decreases the randomness as the iterations proceed. The APSO starts by initializing a swarm of particles with random positions and velocities. The fitness function of each particle is evaluated and the best g value is calculated [14].

Later, actual position is updated for each and every particle. This process is repeated until the optimum best g value is obtained. Some of the advantages of APSO over other traditional optimization techniques, it has the reliability to modify and find a balance between the global and local exploration of the search space, and it has implicit parallelism.

$$ Vel_{n} \left( {t + 1} \right) = w \cdot Vel_{n} \left( t \right) + c_{1 } \cdot r_{1 } \left( {pbest_{n} - X_{n} \left( t \right)} \right) + c_{2 } \cdot r_{2 } \left( {gbest - X_{n} \left( t \right) } \right) $$

(5)

$$ X_{n} \left( {t + 1} \right) = X_{n} \left( t \right) + Vel_{n } \left( {t + 1} \right) $$

(6)

Here, w is the inertia coefficient of the particle which play a vital role in PSO. $Vel_{n } \left( {t + 1} \right)$ is present particle’s velocity, $Vel_{n } \left( t \right)$ is the earlier particle’s velocity, $X_{n} \left( t \right)$ is the present particle’s position, $X_{n} \left( t \right)$ is the earlier particle’s position. r₁ and r₂ are random in nature and lies in the range [0 and 1] and uniformly distributed [15].

c₁ and c₂ are the acceleration constants which manage the relative effect of the pbest and gbest particles. pbest_n is the present pbest value, gbest is the present gbest value.

The PSO algorithm is defined in 4 steps which will terminate when the exit criteria are met. The velocity vector is produced by using the below expression.

$$ Vel_{n} \left( {t + 1} \right) = w\, \cdot \,Vel_{n} \left( t \right) + \alpha \, \cdot \,c_{n } + \beta \left( {gbest - X_{n} \left( t \right)} \right) $$

(7)

Here $c_{n }$ value lies in between (0, 1) and in random nature.

The position vector is modified using the following expression

$$ X_{n} \left( {t + 1} \right) = X_{n} \left( t \right) + Vel_{n} \left( {t + 1} \right) $$

(8)

Combining the above two equations yield the following expressions.

$$ X_{n} \left( {t + 1} \right) = \left( {1 - \beta } \right)X_{n} \left( t \right) + \alpha \cdot c_{n } + \beta \left( {gbest} \right) $$

(9)

The distinctive values of APSO are $\alpha$ = 0.1–0.4 and = $\beta$ 0.1–0.7. Here $\alpha$ is 0.2 and $\beta$ is 0.5.

$$ \begin{array}{*{20}c} {{\text{while}}\,\alpha = \gamma^{t} } & {(0 < \gamma < 1)} \\ \end{array} $$

(10)

$\gamma$ is referred to a control parameter with magnitude 0.9 coherent in the iteration number.

4 Results

Cuckoo search algorithm and Accelerated Particle Swarm Optimization are applied to evaluate amplitude distribution required to maintain sum patterns with Sidelobe level at –35 dB. The patterns are numerically computed for N = 100 arrays of elements by varying the spacing between elements as d = 0.40 and 0.45. As the number of elements are increased in the array, the Null to Null beamwidth is found to decrease (Figs. 2, 3, 4 and 5).

Fig. 2

Amplitude distribution for N = 100 element array with d = 0.40 using Taylor, CSA, and APSO

Fig. 3

Sum pattern optimized for N = 100 array with d = 0.40 and nbar = 6 using Taylor, CSA, and APSO

Fig. 4

Amplitude distribution for N = 100 element array with d = 0.45 using Taylor, CSA, and APSO

Fig. 5

Sum pattern optimized for N = 100 array with d = 0.45 and nbar = 6 using Taylor, CSA, and APSO

5 Conclusion

The synthesis of uniform linear arrays for sidelobe level reduction is considered in the present work. The Algorithms is found to be useful to generate desired radiation pattern. The method is useful to solve multi-objective array problems involving with specified number of constraints. The sidelobe level is decreased to –35 dB. The results are extremely useful in communication and radar systems where the mitigation of EMI is a major concern. The beamwidth remains unaltered even after reducing the sidelobe level. The rise of far away sidelobes is not a problem in the system of present interest.