Keywords

1 Introduction

Open source software (OSS) have become very popular nowadays. OSS are the software whose source code is freely available to user for use, distribution, reproduction and modification as per the user needs under the licensing policies of OSS [1]. Open source software are developed by a single developer or a group of software developers initially but as the attractiveness of the software increases its users and volunteers also increases throughout the whole world. In recent years, people have become more reliant on OSS for their need. The reliability of the software is defined as the probability of the failure free software for a given interval of time in a specific environment [2, 3]. Software reliability is a very important attribute of the software quality, together with functionality, usability, performance, maintainability, capability, installation and documentation [4]. The proponent of the closed source software believe that hackers can easily incorporate the malicious files in the OSS as the source code is freely and easily available [5] but it is for the same fact that the OSS are more reliable than closed source software as thousands of volunteer are involved in the testing process of the OSS.

In software development process, due to availability of limited time and resources, it is not possible to detect all the faults of the software or to develop complete and reliable software in single development cycle [6]. Then, there is a need of up-gradation of the software and develop successive release by adding new functionalities which also helps in competing with other projects and capturing market. But up-gradation of the software is a very difficult task because up-gradation leads to additional faults in the software therefore there is an increase in failure rate after the up-gradation which then decreases gradually due to fault debugging process [6]. To estimate the mean number of faults detected for closed source software, multi up-gradation SRGM was proposed earlier by Kapur et al. [7, 8]. Recently, a number of multi release SRGM’s have been proposed in the litrature for OSS. In 2011, Li et al. [9] proposed a multi attribute utility theory based optimization problem to determine optimal time for releasing next version of OSS. Yang et al. [10] discussed a multi release SRGM for OSS by incorporating fault detection process and fault correction process. Aggarwal et al. [11] proposed a discrete model for OSS which has been released into the market a number of times.

In this paper, we proposed an imperfect debugging based SRGM for OSS model with multiple releases. In the proposed model, bugs introduced during the addition of new add-ons to the current release and some undetected bugs of previous release are considered. This paper is divided into four sections. In Sect. 2, we discuss a multi release SRGM for OSS under the effect of imperfect debugging. In Sect. 3, we present parameter estimation results corresponding to three release fault data sets of Apache project. Finally the conclusions have been drawn in Sect. 4.

2 Modeling Software Reliability

For last few decades, several mathematical models have been proposed that describe the reliability growth of the software during testing process such as Goel and Okumoto [12], Yamada et al. [13]. In most of the models the software failure occurrence has been represented by Non-Homogenous Poisson Process (NHPP). The main focus of NHPP models is to determine the mean value function or the expected number of failure occurrences during a time interval.

Most of the NHPP models are based on the following assumption

  • Failure occurs independently and randomly over time.

  • Initially fault content in the software is finite.

  • The efforts to remove underlying faults once a failure has occurred starts immediately.

  • During testing and debugging process no new faults are introduced (i.e. perfect debugging).

But in case of imperfect debugging, the last assumption does not hold good. There is a possibility that some new faults may be added when detected faults are removed\corrected.

2.1 Model Development

In this section, an NHPP based SRGM is proposed to model reliability growth phenomena for an OSS incorporating imperfect debugging.

  1. a.

    A general NHPP model

Letus assume that the counting process {N(t), t ≥ 0} is a Non-Homogenous Poisson Process, under, these assumption, m(t), the mean value function for the fault removal process may be represented by the following differential equation.

$$\lambda \left( t \right) = \frac{{{\text{d}}m\left( t \right)}}{{{\text{d}}t}} = b\left( t \right)\left[ {a\left( t \right) - m\left( t \right)} \right]$$
(1)

The mean value function for cumulative number of failure, m(t) can be represented as

$$m\left( t \right) = {\text{e}}^{ - B\left( t \right)} \left[ {\int_{0}^{t} {a\left( x \right)b\left( x \right){\text{e}}^{B\left( x \right)} {\text{d}}x} } \right]$$
(2)

where \(B\left( t \right) = \int_{0}^{t} {b\left( x \right){\text{d}}x}\).

  1. b.

    Weibull model

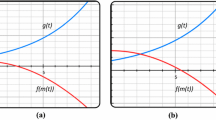
In the case of open source software, when new software is released over the market, the fault removal rate of the OSS is quite distinct from that of the closed source software. In contrast to the closed source software system, OSS are released over the internet with little testing. Once it is released large number of volunteers and enthusiastic testers report bugs through bug tracking system which affect the reliability and attraction of the OSS [14]. Therefore, the fault removal rate (FRR) for OSS initially increases due to growth in the users population but later on decreases as newer versions come into the market and the attractiveness of the present release decreases. Its users shift their loyalty to the other versions/OSS. In order to incorporate such type of increasing and decreasing FRR in the model building [15], we use Weibull distribution function to describe fault removal process (FRP). Weibull distrubution is flexible distribution which may change its shape depending upon different values of its shape parameter (here k) see in Fig. 1. For example,

Fig. 1
figure 1

CDF for weibull distribution

Full size image

  • When k > 0, the rate corresponding to weibull distribution is increasing. In the context of OSS it may represent the phenomenon when more and more users are getting attached to OSS system and as result increasing numbers of faults are being reported through its bug tracking system.

  • When k = 1, this indicates constant rate of failure and it represent the case when an OSS has reached it maturity level with respect to its number of users.

  • When k < 1, here failure rate is decreasing, this may occur when users are shifting due the availability of newer version on the internet.

The following differential equation using Weibull model may be formulated to measure the expected number of faults removed,

$$\frac{{{\text{d}}m\left( t \right)}}{{{\text{d}}t}} = bt^{k} \left( {a - m\left( t \right)} \right)$$
(3)

Under the initial condition that, \(m\left( t \right) = 0\,{\text{at}}\,t = 0\), the above differential equation gives the following result

$$m\left( t \right) = a\left[ {1 - {\text{e}}^{{ - b\frac{{t^{k + 1} }}{k + 1}}} } \right] = aF\left( t \right)$$
(4)

where \(m\left( t \right)\) represents expected mean number of faults removed and \(F\left( t \right) = \left[ {1 - {\text{e}}^{{ - b\frac{{t^{k + 1} }}{k + 1}}} } \right]\) is CDF of weibull distribution with shape parameter \(k( > 0)\), also known as weibull slope. Let us assume that the debugging process is not perfect over t, some new faults are introduced in the code during correction efforts [5]. Therefore the fault content of the software at time t is given as…

$$a\left( t \right) = a + \alpha m\left( t \right)$$
(5)

Here \(\alpha\) is the constant rate at which new faults are introduced. Then, the Weibull model for open source software under the effect of imperfect debugging will be

$$m\left( t \right) = \frac{a}{1 - \alpha }\left[ {1 - {\text{e}}^{{ - b\left( {1 - \alpha } \right)\frac{{t^{k + 1} }}{k + 1}}} } \right].$$
(6)

2.2 Multi Release Model with Imperfect Debugging

$${\text{Let}}\;{\text{us}}\;{\text{assume}}\;a_{i}^{*} = \frac{{a_{i} }}{{1 - \alpha_{i} }}\;{\text{and}}\;F_{i} \left( t \right) = 1 - {\text{e}}^{{ - b_{i} \left( {1 - \alpha_{i} } \right)\frac{{\left( {t - \tau_{i - 1} } \right)^{{k_{i} + 1}} }}{{k_{i} + 1}}}}$$
(7)

where \(F_{i} \left( t \right)\) is the CDF of weibul model for ith release. The mathematical expression for fault removal under imperfect debugging for the ith release can be shown as.

$$m_{i} \left( t \right) = \left[ {a_{i}^{*} + \left[ {a_{i - 1}^{*} - m_{i - 1} \left( {\tau_{i - 1} } \right)} \right]} \right]F_{i} \left( t \right)\quad {\text{for}}\;\;\tau_{i - 1} \le t < \tau_{i}$$
(8)

The mathematical expressions for the number of faults removed during different releases are given as follows:

For release 1

When first release of the software comes in the market at time \(\tau_{1}\), it is tested before being introduced into the market. In the testing process, testing team tries to detect and correct maximum number of the bugs of the software. But practically it is not possible to detect all the faults of software, so testing team can detect only a finite number of bugs in the software which are less than the total fault content of the software [7]. The following equation represents the number of faults removed during testing of release 1.

$$m_{1} \left( t \right) = a_{1}^{*} F_{1} \left( t \right)\tau_{0} \le t < \tau_{1}$$

For release 2

Improved technology, rising competition and dynamic nature of market makes rise to the need of software up-gradation. Addition of new features and functions to the existing version of software can increase the probability of survival and adoption in the market. When new code is added some new faults are introduced into the code. These additional faults along with the fault content of previous release are corrected during the testing of second release with a new FDR [7]. Considering \(\left[ {\tau_{1} ,\tau_{2} } \right)\) is the time interval for testing and at time \(\tau_{2}\) testing of release 2 is stopped and launched into the market. Then, the number of faults removed can be represent as

$$m_{2} \left( t \right) = \left[ {a_{2}^{*} + \left[ {a_{1}^{*} - m_{1} \left( {\tau_{1} } \right)} \right]} \right]F_{2} \left( t \right)\tau_{1} \le t < \tau_{2}$$

For release 3

In this release, the faults due to add-ons and left over fault content of release 2 are considered for removal process. Here we assume that during the testing of release 3 the faults of current version and just previous version are removed, do not take into consideration the undetected faults of version 1, which may be present in the code of version 3. It help us to keep the model simple and easy for parameter estimation. Let \(\tau_{3}\) be launched time for release 3. Then FRP for release 3 is given by

$$m_{3} \left( t \right) = \left[ {a_{3}^{*} + \left[ {a_{2}^{*} - m_{2} \left( {\tau_{2} } \right)} \right]} \right]F_{3} \left( t \right)\tau_{2} \le t < \tau_{3}$$

In the same manner, we can model FRP for the subsequent releases of the OSS. In the next section we discuss how to validate model to the real life application.

3 Data Set and Analysis

Data sets for three versions of Apache are considered for the validation of the proposed model. The data sets of Apache 2.0.35 (first release), Apache 2.0.36 (second release) and Apache 2.0.39 (third release) are used for the estimation of model parameters [9]. During 43 days of testing for first release (Apache 2.0.35) 74 faults were detected. For the second releases (Apache 2.0.36) testing was carried out for 103 days and 50 faults were detected. For release third (Apache 2.0.39) during 164 days 58 faults were detected.

For estimation of the parameters of the proposed model, the Least Square Estimation Method is used. In the field of Software Reliability Least Square Estimation Method is one of the commonly used methods [3]. SPSS, ‘The Statistical Package for Social Sciences’ software is applied for estimation of parameters \(a_{i} , \,b_{i} ,\,\alpha_{i } \,{\text{and}}\,k_{i}\) of ith release from the data sets. The estimated parameters of each release are demonstrated in Table 1. The proposed model is then compared with the Amir Garmabaki et al. reliability model [6]. For comparison purpose we have selected Amir et al. reliability model [6] because it proposes a multi release open source software reliability model under perfect debugging conditions. In our model we have incorporated error generation in the modeling framework. By comparing these two models, we can analyze the benefit of imperfect debugging based models. For comparison we have used important criteria (Coefficient of Multiple Determination \(\left( {R^{2} } \right)\) and Mean Square Error (MSE)), the goodness of fit analysis results are given in Table 2. From the result it may be observed that the proposed model provides better fit to the data in comparison to Amir et al. reliability model. The values of MSE and Ad-R2 corresponding to the proposed models are better than Amir et al. reliability model [6]. The goodness of fit of our model may be further judge by looking Figs. 2, 3 and 4. It may be observed that estimated value is quite near to actual value for all the three releases. From the Table 1 we may observed the value of parameter \(\alpha\) is highest for release 1 of Apache software as compared to other two versions. It indicates higher rate of error generation for the initial release as compared to subsequent releases. It may occur due to the fact that when the project is new then chances of introducing additional faults during debugging efforts are higher.

Table 1 Parameter estimation results
Full size table
Table 2 Comparison criteria results
Full size table
Fig. 2
figure 2

Goodness of fit for first release

Full size image
Fig. 3
figure 3

Goodness of fit for release 2

Full size image
Fig. 4
figure 4

Goodness of fit for release 3

Full size image

  • Coefficient of Multiple Determination \(\left( {R^{2} } \right)\)

It shows how much proportion of the variation of the data get explained by the regression model and it measure of the goodness of fit of the model, higher the value of R-squared, More the model fits to data.

$$R^{2} = 1 - \frac{{{\text{residual}}\,SS}}{{{\text{corrected}}\,SS}}$$

  • Mean Square Error

It is the mean of the square of the difference between the expected values and the observed value,

$${\text{MSE}} = \mathop \sum \limits_{i = 1}^{k} \frac{{\left( {m^{\prime } \left( {t_{i} } \right) - y_{i} } \right)}}{k}$$

Here, k represents the number of observation. Better the goodness of fit to data if the MSE is lower. Figures 2, 3 and 4 shows the Goodness of fit for the three release of Apache respectively.

4 Conclusion

In this era of Information technology OSS represents a paradigm shift in the software development life cycle. Unlike in closed source software where testing is performed by a group of testers, OSS is tested by millions of spontaneous volunteers during its operational phase. In this paper, we use Weibull probability distribution function to model FRP of OSS so as to represents the initial increase and finally decrease in the bug reporting of OSS. As the entire bug reporting are not valid. Therefore the concept of imperfect debugging has been incorporated in model building. Proposed model has been validated on a 3 releases fault data sets of well-known OSS namely, Apache. The results on compared with other well-known model [6] to illustrate the accuracy of model and goodness of fit. In future we may extend the model to relate growth in the user population to the faults removed during debugging process.