Abstract
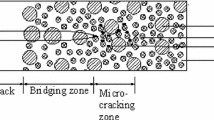
Concrete is considered as a homogeneous material from a design perspective. However, on a close examination, it is observed that concrete is heterogeneous, which consist of coarse aggregate and fine aggregate embedded in cement paste. Further, there exists an interfacial region, which bonds the aggregate with the cement paste. The strength of this interfacial transition zone (ITZ) depends on its microstructural characteristics. This interfacial region neither possesses the properties of aggregate nor of the cement paste. Interface being the weakest zone, the microcracks are likely to initiate here when the local major principal stress exceeds the initial tensile strength of the interface. When these microcracks reach certain critical length, it propagates and coalesces with the existing macrocrack to form a major crack resulting in the failure of the bond. The microstructural character of the interfacial zone governs the mode I crack propagation in conventional concrete . The material behavior of concrete is influenced by the geometry, the spatial distribution, and the material property of the individual constituents and their interactions. This study aims at estimating the critical microcrack length using the principles of linear elastic fracture mechanics (LEFM) by analyzing the crack opening displacement at different scales. Also, a procedure to determine the material properties such as the elastic modulus and fracture toughness at the interface by knowing the concrete mix proportion is explained.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
During mixing of concrete , the shearing stress exerted on the cement paste by the aggregates tends to separate water from cement particles and results in a small region around the aggregate particles with fewer cement particles termed as the ITZ [1]. The composition of this zone was found to be different from that of cement paste as the density of cement particles was lesser than that of its surroundings. Although several techniques such as X-ray diffraction, X-ray photoelectron spectroscopy, secondary ion mass spectroscopy, mercury intrusion porosimetry, optical microscope, and electron microscope have been employed to study the ITZ, the complete characterization of the distinctive features of this zone has still not been achieved. The interface acts as a bridge between aggregate and the cement paste, which neither possesses the properties of aggregate nor the cement paste.
Upon loading, microcracking initiates in the ITZ when the local major principal stress exceeds the initial tensile strength of the interface [2]. Ansari [3] reported that the macrocrack would occur only when the microcrack reaches a critical length. This critical microcrack propagates and coalesces with existing macrocrack thereby resulting in the failure of the bond. The stiffness of the interface decreases although the individual components on either side of the interface possess high stiffness. This is due to the presence of voids and microcracks in this region, which do not allow the transfer of stress.
The packing and density of the cement particle around the aggregates define the strength of the interfacial zone. The strength of an interface decides whether a crack should grow around an aggregate particle or through the aggregate. Also, the fracture energy of the interface is found to be less than that of the cement paste and aggregate. The microstructural character of the interfacial zone governs the mode I crack propagation in concrete [4]. Thus, the material behavior of concrete is influenced by the geometry, the spatial distribution, and the material property of the individual material constituents and their mutual interaction. Hence, the failure of concrete structure can be viewed as a multiscale phenomenon, wherein the information of the material properties at a microlevel can be used to determine the system behavior at the macrolevel.
In this paper, the critical length of the microcrack present in the ITZ is estimated using the principles of linear elastic fracture mechanics. This is achieved by relating the crack opening displacements at two different scales, namely micro and macro. A procedure to determine the material properties at the ITZ including the elastic modulus and the fracture toughness by knowing the mix proportions of the ingredients in concrete is explained. The critical microcrack length thus determined can be treated as a material property and can be used further in predicting the macroscopic behavior of concrete .
2 Critical Microcrack Length
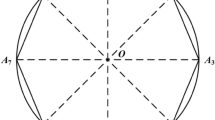
The initiation and propagation of microcrack at the interface between the cement paste and the aggregates are attributed to the toughness of the interface. In this study, the critical microcrack length is a parameter, which is used to characterize the interface. As the critical microcrack length increases, the toughness of the interface increases. Thus, it influences the overall strength of concrete . The existence of microcrack and restraining stress at the macrocrack tip is a well-known fact. Upon loading, the microcrack will initiate at the interface and later coalesce with the existing macrocrack resulting in the crack increment. In this study, the critical length of the microcrack is determined by analyzing a small element near the macrocrack tip and along the interface between the cement paste and aggregate, as depicted in Fig. 1.
The following assumptions are made in the derivation of the critical microcrack length: (1) The microcrack grows in a direction perpendicular to the maximum principal stress. (2) The initial microcrack length is assumed to be much smaller than the size of the element considered. (3) The microcrack tip is sharp for linear elastic fracture mechanics to be applied.
The stresses and displacement along the crack tip for this two-dimensional crack problem are determined through an inverse method by making use of an Airy stress function (Ф), which satisfies the biharmonic equation (∇2∇2 Ф = 0). The stresses and strains in the polar coordinate system are further determined. Using these strains, the displacements in the polar coordinate system are obtained as
In the above equations, μ micro and ν micro are the shear modulus and the Poisson’s ratio of the interface, respectively, where the microcrack is likely to occur. The microcrack present in the interface is assumed to be sharp in order to initiate the crack propagation. The crack surface of the microcrack is considered as stress free, and the corresponding boundary conditions along the upper surface denoted by (+) and lower surface denoted by (−) are given by
Assuming the microcrack to be very sharp, the microcrack angle attains a value of π, and the characteristic equation reduces to sin(2λ n π) = 0. The roots of this characteristic equation give the eigenvalues (λ n = n/2; n = 0, ±1, ±2, …). The crack-tip singularity is observed when the eigenvalue becomes 0.5. The displacement field near the microcrack tip reduces to the following form
A relationship between B 1 and D 1 is obtained by substituting the eigenvalue into the boundary condition (B 1 = D 1/3). This reduces the displacement field in terms of one unknown parameter D 1. Further, by defining D 1 = K 1/√(2π), the displacement field becomes a function of stress intensity factor (K). The crack opening displacement corresponding to the microcrack is determined by transforming the displacement component perpendicular to the loading direction (V) into rectangular coordinates by making use of the following transformation
By substituting θ = +β * and θ = −β *, the displacement field along the upper (V +) and the lower (V −) surface of the crack is obtained. The corresponding displacement fields are given by
The following equation provides the corresponding microcrack opening displacement (δ micro):
As the microcrack initiates in the interfacial region, the stress intensity factor (K), elasticity modulus (E), and r are replaced with K Interface, E Interface, and l/2 (as the total length of microcrack is assumed to be l as in Fig. 2). When the microcrack reaches a critical length (i.e., l = l c ), the corresponding fracture toughness and crack opening displacement reach their critical value (K Interface IC , δ c ) and are given by,
Microcracks are nucleated in concrete structure when the applied load reaches 80% of peak load. When the applied load reaches the peak load, the microcrack becomes critical, and it coalesces with the macrocrack. Figure 2 represents the existence of the microcrack at the macrocrack tip considered in this study.
The macrocrack length and the stress corresponding to the peak load (P peak) are represented as the critical macrocrack length (a c ) and peak stress (σ p ). The crack length corresponding to the peak load is determined by knowing the crack mouth opening displacement (δ p ) at the peak load. The following equation provides the crack opening displacement at any point (x) along the macrocrack:
where E is the elastic modulus of concrete , D is the depth of the specimen, and the geometric factors g 2(a c /D) and g 3(x/a c , a c /D) for beam specimen are taken from standard reference [5]. From Fig. 2, it is clear that the crack opening displacement due to the macrocrack at (x = a c − l c /2) will be equal to the crack opening displacement due to the microcrack at r = l c /2. The critical microcrack length is determined by equating both the crack opening displacements that are given by Eqs. (11) and (12). The solution of the following equation gives the critical microcrack length.
As seen from the above equation, the critical microcrack length can be obtained by knowing the fracture toughness and elastic modulus of the interfacial zone. The procedure for estimating the interfacial properties is explained in the following section.
3 Estimation of Interfacial Properties
3.1 Interfacial Fracture Toughness
The lower density of cement particles around the aggregates makes the interface weaker. The initiation and propagation of a microcrack depend on the toughness of the interface. Hillemier and Hilsdorf [6] conducted experiments and analytical investigations to determine the fracture properties of hardened cement paste, aggregate, and cement-paste interface. Huang and Li [7] considered the nucleation of a crack along the interface of aggregate and mortar and derived a relation between the effective toughness of the material and the mortar in terms of volume fractions by considering the crack deflection and interfacial cracking effects, which is
where K IC is the fracture toughness of concrete , K m IC is the fracture toughness of mortar, V f (ca) is the volume fraction of coarse aggregate, and ν eff is the Poisson’s ratio of concrete . In this work, a relation between the toughness of matrix and cement paste is derived by suitably modifying and replacing the fracture toughness of concrete and mortar with those of mortar and cement paste. Also, the volume fraction of coarse aggregate and Poisson’s ratio of concrete is replaced with that of fine aggregate and Poisson’s ratio of mortar, which takes the form
The fracture toughness of cement paste–aggregate interface is much lower than that of cement paste. Hillemier and Hilsdorf [6] conducted experiments to determine the fracture toughness of the interface and the cement paste and observed the toughness of the interface to be 0.4 times of the cement paste (i.e., K Interface IC = 0.4 K cp IC ), which is used in the present study.
3.2 Interfacial Elastic Modulus
The elastic modulus of the interface is another major parameter used to define the critical microcrack length (l c ) and is reported to be 0.7 times the elastic modulus of cement paste (E cp ) [8] and is used in this study. Hashin [9] obtained a relation between the elastic modulus of homogeneous material with and without inclusion, based on volume fraction and modulus of the inclusion by considering the change in the strain energy of a loaded homogeneous body due to the insertion of inhomogeneities using the variational theorems in the theory of elasticity. Accordingly, the relation between the elastic modulus of concrete and mortar is expressed as,
where V f (m) and V f (ca) are the volume fraction of mortar and coarse aggregate, and E, E m , and E ca are the elastic modulus of concrete , mortar, and coarse aggregate, respectively. The above equation can be simplified to the form,
The elastic modulus of the mortar is obtained by solving the above quadratic equation. The relationship between the modulus of elasticity of mortar and cement paste is obtained in a similar manner by replacing the material properties of concrete and mortar with the properties of mortar and cement paste. Also, the volume fraction of coarse aggregate and mortar is replaced with those of fine aggregate and cement paste. The modulus of elasticity of cement paste is determined by solving the following quadratic equation.
where V f (cp) and V f (fa) are the volume fraction of cement paste and fine aggregate, and E m , E cp , and E fa are the elastic modulus of mortar, cement paste, and fine aggregate, respectively.
4 Analysis of Experimental Data
The interfacial properties, such as the modulus of elasticity and fracture toughness and the critical microcrack length as discussed in the previous section, are evaluated for normal strength concrete used by researchers in their experimental program. The following experimental data are considered in this analysis: Bazant and Xu [10] and Shah and Chandra Kishen [11]. In both research works mentioned above, tests have been carried out on beams of three different sizes (designated as small, medium, and large), which are geometrically similar under three-point bending. Table 1 shows the dimensions of the beams, the peak stress, and the crack mouth opening displacement (CMOD) at peak load. The material properties, including the fracture toughness and elastic modulus as reported in these experimental works, are given in Table 2. The mix proportion used in the experiments conducted by Bazant and Xu [10] and Shah and Chandra Kishen [11] are 1:1.86:2.61:0.54 and 1:2:2:0.6, respectively.
As discussed in the previous sections, the interfacial properties of concrete depend on the volume fraction of each of its constituents. The interfacial fracture toughness, the interfacial elastic modulus, and the critical microcrack length, calculated using the above-mentioned procedure, are tabulated in Tables 2 and 3. It is seen that the interface is the weaker region and is therefore more prone to cracking and that justifies the analysis of the interfacial region. Furthermore, as reported in the literature [5], if the interface is weaker than the coarse aggregates, the crack propagates around the aggregate. In Table 2, it is also observed that for a particular concrete mix, the computed interfacial properties remain constant.
As reported in Table 3, the critical microcrack length is found to be dependent on the properties of the interface as well as the geometry of the specimen. Also, it is found to be increasing with the size of the specimen, even though the interfacial properties remain the same. Also, Mobasher et al. [12] have reported that 80% of microcracks are smaller than 1.5 mm in length. The critical length of microcrack is found to be comparable with the size of the fine aggregate and cement particles. Further, the critical microcrack length is normalized with the depth of beam as shown in Table 3. It is seen that this normalized value remains almost constant for a given mix of concrete and could be treated as a material property.
5 Conclusions
In this study, a critical microcrack length parameter is defined, and an expression is derived by analyzing the crack opening displacement at micro- and macroscales. The critical microcrack length is found to be dependent on the specimen size. Also, it is observed that, for a particular mix of concrete , the ratio of critical microcrack length to the specimen depth is found to be constant and can be used as a material property. The critical microcrack thus determined can be further used in predicting the macroscopic behavior of concrete .
References
J.C. Maso, Interfacial transition zone in concrete, RILEM report, vol. 11 (CRC Press, UK, 2004)
Iulia Carmen Mihai and Anthony Duncan Jefferson, A material model for cementitious composite materials with an exterior point eshelby microcrack initiation criterion. Int. J. Solids Struct. 48, 3312–3325 (2011)
Farhad Ansari, Mechanism of microcrack formation in concrete. ACI Mat. J. 86, 459–464 (1989)
J.G.M. Van Mier, A. Vervuurt, Numerical analysis of interface fracture in concrete using a lattice-type fracture model. Int. J. Damage Mech 6, 408–432 (1997)
S.P. Shah, S.E. Swartz, C. Ouyang, Fracture mechanics of concrete: applications of fracture mechanics to concrete, rock and other quasibrittle materials. (Wiley, NY, 1995)
B. Hillemeier, H.K. Hilsdorf, Fracture mechanics studies on concrete compounds. Cem. Concr. Res. 7, 523–535 (1977)
J. Huang, V.C. Li, A meso-mechanical model of the tensile behavior of concrete. Part II: modelling of post-peak tension softening behavior. Composites 20, 370–378 (1989)
C.C. Yang, Effect of the transition zone on the elastic moduli of mortar. Cem. Concr. Res. 28, 727–736 (1998)
Zvi Hashin, The elastic moduli of heterogeneous materials. J. Appl. Mech. 29, 143–150 (1962)
Z.P. Bazant, K. Xu, Size effect in fatigue fracture of concrete. ACI Mat. J. 88, 390–399 (1991)
S.G. Shah, J.M. Chandra Kishen, Fracture properties of concrete–concrete interfaces using digital image correlation. Exp. Mech. 51, 303–313 (2011)
B. Mobasher, H. Stang, S.P. Shah, Microcracking in fiber reinforced concrete. Cem. Concr. Res. 20, 665–676 (1990)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Simon, K.M., Chandra Kishen, J.M. (2018). Estimation of Critical Microcrack Length in Concrete by Considering Interfacial Properties. In: Prakash, R., Jayaram, V., Saxena, A. (eds) Advances in Structural Integrity. Springer, Singapore. https://doi.org/10.1007/978-981-10-7197-3_13
Download citation
DOI: https://doi.org/10.1007/978-981-10-7197-3_13
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-7196-6
Online ISBN: 978-981-10-7197-3
eBook Packages: EngineeringEngineering (R0)