An Elitist Non-dominated Sorting Hybrid Evolutionary Algorithm for Multi-objective Constrained Ship Arrangements Optimization Problem

Abstract

As the complexity of ship arrangements increases, general arrangements optimization technology based on evolutionary algorithms has emerged, giving enormous potential to assist designers in enhancing the range of alternative arrangements and in expediting the design process. This paper presents a hybrid evolutionary algorithm to handle the multi-objective constrained arrangements optimization problem based on elitist non-dominated sorting strategy. To enhance the efficiency of optimization, a hybrid evolutionary algorithm that couples an NSGA-II with a stochastic local search technique is used to find feasible solutions rapidly and facilitate local optimization. However, the algorithm that can rapidly find feasible solutions is also expected to contribute to better optimization. It has also been observed that lack of diversity of potential solutions leads to a local optimal solution which means the coherent arrangements could not be discovered. Hence, a modified replacement strategy is proposed to overcome this drawback. The final experimental results illustrate that the algorithm is capable of generating coherent arrangements.

1 Introduction

The arrangements optimization problem consists of determining the best size and position for shipboard elements on several ship decks. The optimal goals and constraints can be divided into two aspects, those of topology and geometry. The arrangements optimization problem is one of the classical Non-deterministic Polynomial Complete problems [1]. Moreover, the large number of variables and constraints are the most significant features of arrangements optimization. The large number of variables results in very high-dimensional and vast search spaces. On the other hand, the large number of constraints makes the feasible solution spaces become discrete and tiny relative to the search space. The ability to find quick solutions is a challenging task in the arrangements optimization problem.

Generating general arrangements is a crucial part of ship design. The traditional general arrangements design method is a repetitive trial-and-error procedure, where different dimensions and positions of elements are adjusted until a feasible arrangement, satisfying design requirements, emerges. During the past 30 years, the attention to ship arrangements optimization has been steadily increasing. Cort and Hills [2] developed a manual iterative process for ship arrangements optimization. The opportunities and challenges within the optimization depend on the experience and inspiration of designers. Andrews [3,4,5] proposed a function building block approach that is still a manual optimization. As the complexity of ship arrangements increases, the design process may become tedious and time consuming for humans.

The use of computers and evolutionary techniques that are capable of generating and contrasting enormous layout schemes have become an effective and practical way for handling complicated arrangements design. Lee [6,7,8] used a GA to derive solutions for ship compartment layout problems. Inner walls and passages were considered during the optimization. Kim [9] proposed an expert system and a multistage optimization for submarine arrangement design. Ölçer [10, 11] used an integrated multi-objective algorithm and decision-making techniques to determine the subdivisions arrangement of a ro-ro passenger ship. Parsons [12], Nick [13] and Daniels [14, 15] proposed a semi-automated approach—Intelligent Ship Arrangements (ISA) that generates arrangements in an agent-genetic process driven by constraints and a single objective. The shipboard elements are firstly allocated to pre-defined zone-decks; subsequently, the assigned elements are arranged in each zone-deck. Gillespie [16, 17] used a network partitioning method to identify the interaction among ship elements that have a fixed area and developed a non-spatial, network theory-based approach to assign shipboard items to structural zones. Oers [18,19,20,21,22] developed a packing approach combined with NSGA-II to generate three-dimensional ship configurations. Each shipboard element was assumed as a cubic unit. It is noted that a packing density objective and a constant objective were used by NSGA-II to enable the search process to proceed successfully. The NSGA-II is not necessary to generate a set of Pareto-optimal solutions in this study, but generates a large and diverse set of feasible arrangements where designers could subsequently choose an optimal solution based on their own judgment.

However, the problem of arrangements optimization was studied beyond the field of ship design. Pan [23] proposed a region division based diversity maintaining approach for crashworthiness design of vehicles. Within the field of architecture, Rodrigues et al. [24,25,26] used an evolutionary approach to multi-level space allocation problems. In this case, seven different evaluators were mentioned and aggregated in a single objective function subject to minimization. In other applications, such as the Facility Layout Problem, a new adaptive algorithm was proposed for a facility layout [27]. In this case, the departments’ sizes are not predetermined.

The reviewed literature related to ship arrangements optimization indicates that most previous studies considered arrangements optimization as deterministic optimization, in which the size of shipboard elements is assumed to be constant. In addition, the majority of researchers formulated the arrangements optimization as a single objective optimization problem.

This paper presents an elitist non-dominated sorting hybrid evolutionary technique to the ship arrangements optimization problem, in which size and position of shipboard elements are considered as optimal variables. Three objectives representing the separation relationships, circulation efficiency and compactness are introduced to search a set of competitive design solutions.

The rest of this paper is organized as follows: Sect. 2 presents the problem formulation and how objectives and constraints are computed within the mathematical model. Section 3 describes the enhancement that couples an NSGA-II with a stochastic local search technique and the modified replacement strategy in detail. The simulation results are presented in Sect. 4. The stochastic local search technique and modified replacement strategy are discussed in Sect. 5. And, finally, the paper is concluded in Sect. 6.

Table 1. Basic nomenclature

2 Mathematical Model

In this section, the formulation of the arrangements optimization problem is described, and the basic nomenclature and definitions used are listed in Table 1.

2.1 Problem Formulation

The ship arrangements optimization problem can be defined as an allocation of a set of predetermined shipboard elements ${\varvec{E}}=\{\textit{E}_1,\textit{E}_2\dots \textit{E}_N\}$ on multi two-dimensional deck spaces ${\varvec{S}}\,=\,\{\textit{S}_1,\textit{S}_2\dots \textit{S}_N\}$, which satisfy the topological relations and geometric requirements.

The shipboard elements are assumed to be rectangular. Each element ${E}_i({x}^i,{y}^i,{z}^i,{s}^i,{r}^i,{h}^i,{o}^i)$ is determined by seven variables. The ${x}^i,{y}^i,{z}^i$ are the left bottom vertex point coordinate. It is noted that the area s $^i$ and aspect ratio r $^i$ may be intuitive to define the boundary conditions of optimization for the user, but increase the computational complexity. Hence, the length l $^i$ and width w $^i$ calculated by Eqs. (1) and (2) would be used during the search process.

(1)

(2)

Each deck space ${S}_i({x}^i,{y}^i,{z}^i,{l}^i,{w}^i)$ is a rectangle controlled by five variables, and all elements must be inside the deck space. The main deck space S $_1$ is dependent on the ship’s hull and is predetermined before optimization. The upper deck spaces S $_i$ such as bridge deck space, would be decided upon during optimization according to the arrangements on the lower decks.

Different topological attributes would be assigned to each element according to their category and function before optimization. The separation attributes matrix R, material flow cost matrix Mc and material flow frequency matrix Mf would be involved in this study.

2.2 Objective Functions and Constraints

The optimization is an evolving process of a population consisting of individuals. Each individual considered in the optimization contains the size and position of all shipboard elements. And the evolving process is the transformation of those individuals with the purpose of improving their performances and satisfying their requirements. In this paper, three objective functions named Separation, Adjacency and Compactness are introduced to evaluate the topological and geometrical performance of each individual.

The Separation Function expressed by Eq. (3) is used to assess the area utilization efficiency of main deck space and the separation relationship satisfaction among shipboard elements.

$$\begin{aligned} minf_1 =\root 3 \of {|\sum _{i=1}^{N}(s^i \cdot \varphi ^i )/(l^1 \cdot w^1 )-\theta |\cdot min (U )\cdot \sum _{i=1}^{N-1}\sum _{j=i+1}^{N}{} U_{ij} /(N !/2)} . \end{aligned}$$

(3)

where l $^1$ and w $^1$ are the length and width of the main deck space, and $\theta$ is the most efficient use of deck area. In this study, $\theta$ = 0.65. $\varphi ^i$ is used to determine whether element E $_i$ is on the main deck. If element E $_i$ is on the main deck, $\varphi ^i$ would be equal to 1. Otherwise, $\varphi ^i$ would be equal to 0. U is the separation relationship satisfaction matrix and U $_{ij}$ determined by Eqs. (4)–(9) represents the separation relationship satisfaction between element E $_i$ and element E $_j$.

$$\begin{aligned} U_{ij} = \left\{ \begin{array}{ll} R_{ij} ,&{} D_{ij} \le t_{low} \\ R_{ij} \cdot [1+(D_{ij} -t_{low} )/(t_{low} -t_{up} )],&{} t_{low}<D_{ij} \le t_{up} \\ 0,&{} t_{up} <D_{ij} . \end{array} \right. \end{aligned}$$

(4)

$$\begin{aligned} D_{ij} =max (DX_{ij} ,DY_{ij} ) . \end{aligned}$$

(5)

$$\begin{aligned} DX_{ij} = \left\{ \begin{array}{ll} fl_{ij} ,&{} fl_{ij} >0\\ 0,&{} fl_{ij} \le 0 . \end{array} \right. \end{aligned}$$

(6)

$$\begin{aligned} DY_{ij} = \left\{ \begin{array}{ll} fw_{ij} ,&{} fw_{ij} >0\\ 0,&{} fw_{ij} \le 0 . \end{array} \right. \end{aligned}$$

(7)

$$\begin{aligned} fl_{ij} =max (x^i +l^i ,x^j +l^j )-min (x^i ,x^j )-(l^i +l^j ) . \end{aligned}$$

(8)

$$\begin{aligned} fw_{ij} =max (y^i +w^i ,y^j +w^j )-min (y^i ,y^j )-(w^i +w^j ) . \end{aligned}$$

(9)

The Adjacency Function expressed by Eq. (10) is used to assess adjacency relationship satisfaction based on the total cost of material flow. If there is logistical flow between two elements E $_i$ and E $_j$, the path distance dp $_{ij}$ of E $_i$ and E $_j$ would be calculated as rectilinear distance by Eq. (11). $\delta$ is a coefficient which is used to calculated the distance increment due to both elements in different ship decks.

$$\begin{aligned} minf_2 =\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}(dp_{ij} \cdot Mc_{ij} \cdot Mf_{ij} ) . \end{aligned}$$

(10)

$$\begin{aligned} dp_{ij} = \left\{ \begin{array}{ll} fl_{ij} +fw_{ij} +|z^i -z^j |\cdot \delta ,&{} {} fl_{ij}>0\quad and\quad fw_{ij}>0\\ fl_{ij} +|z^i -z^j |\cdot \delta ,&{} fl_{ij}>0\quad and\quad fw_{ij} \le 0\\ fw_{ij} +|z^i -z^j |\cdot \delta ,&{} fl_{ij} \le 0\quad and\quad fw_{ij} >0\\ |z^i -z^j |\cdot \delta ,&{} fl_{ij} \le 0\quad and\quad fw_{ij} \le 0 . \end{array} \right. \end{aligned}$$

(11)

The Compactness Function expressed by Eqs. (12)–(14) is used to assess the compactness of the arrangements. When the arrangement is neat and compact, partial boundaries of the elements would be the common boundaries. This means that the total elements’ perimeters of the compact arrangement plan would be smaller.

$$\begin{aligned} minf_3 =\sum _{i=1}^{N}[2\times (l^i +w^i )]-\sum _{i=1}^{N-1}\sum _{j=i+1}^{N}(pl_{ij} +pw_{ij} ) . \end{aligned}$$

(12)

$$\begin{aligned} pl_{ij} = \left\{ \begin{array}{ll} -fl_{ij} ,&{} fl_{ij} <0\quad and \quad fw_{ij} =0\\ 0,&{} otherwise . \end{array} \right. \end{aligned}$$

(13)

$$\begin{aligned} pw_{ij} = \left\{ \begin{array}{ll} -fw_{ij} ,&{} {} fw_{ij} <0\quad and \quad fl_{ij} =0\\ 0,&{} otherwise . \end{array} \right. \end{aligned}$$

(14)

The Constraint Functions expressed by Eqs. (15)–(17) are used to guarantee that there is no overlap among elements. The overlap is decomposed into a sub-overlap in x-coordinate and a sub-overlap in y-coordinate. Only if both sub-overlaps are merged, would there be overlaps in the deck spaces.

$$\begin{aligned} (xol_{ij} -|xol_{ij} |)\cdot (yol_{ij} -|yol_{ij} |)=0 . \end{aligned}$$

(15)

$$\begin{aligned} xol_{ij} = (x^i +l^i -x^j )\cdot (x^i -x^j -l^j ) . \end{aligned}$$

(16)

$$\begin{aligned} yol_{ij} = (y^i +w^i -y^j )\cdot (y^i -y^j -w^j ) . \end{aligned}$$

(17)

3 A Hybrid Evolutionary Algorithm

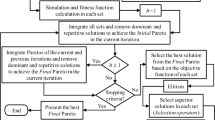
Determining arrangements optimization can be difficult due to the large size of the search space and the complexity of constraints. The Elitist Non-Dominated Sorting Genetic Algorithm (NSGA-II) has proven to be an effective method to determine multi-objective constrained optimization. However, such heuristic methods only handle a reduced set of design variables and constraints. In order to better address large-scale design variables and constraints, a hybrid evolutionary algorithm based on the NSGA-II method is used to achieve a faster convergence of search towards Pareto-optimal front and obtain a diversified solution set. In this section, the details of the elitist non-dominated sorting hybrid evolutionary algorithm are described.

3.1 Chromosome Encoding

Chromosome encoding is an important component of evolutionary algorithms. In the arrangements optimization problem, each chromosome represents a general arrangement scheme. For an arrangements optimization problem that involves N shipboard elements, each chromosome is composed of 7N genes. The first 3N genes of the chromosome represent the bottom vertices x-, y-, z-coordinates of N elements, respectively. The next 3N genes represent the length l $^i$, width w $^i$ and height h $^i$ of each element. The last N gene represents the orientation. It is noted that the length l $^i$ and width w $^i$ of elements are used for convenience in the chromosome encoding rather than area s $^i$ and aspect ratio r $^i$. The z-coordinates z $^i$ and height h $^i$ of elements are assumed as constant in this study. The real coding is adopted, and a solution and its corresponding chromosome v can be formulated as follow:

$$\begin{aligned} v =[x^1 \dots x^N ,y^1 \dots y^N ,z^1 \dots z^N ,l^1 \dots l^N ,w^1 \dots w^N ,h^1 \dots h^N ,o^1 \dots o^N ] \end{aligned}$$

(18)

3.2 Genetic and Stochastic Local Search Operators

As mentioned earlier, the proposed algorithm couples the NSGA-II with a stochastic local search technique to facilitate local optimization. During both search processes, the individuals are subject to a series of adaptive stochastic operators that perform positional and dimensional transformation of elements. The genetic operators that include both crossover and mutation operators are used to generate new offspring P $_i^{'}$ from the parent P $_i$. And the stochastic local search operators containing both geometric and topological operators are applied to the individuals in offspring P $_i^{'}$ for generating the new population P $_i^{''}$. After genetic and stochastic local search operations have been carried out, the individual’s objective function values and constraint violation are calculated. Then a combined population ${Q}_i={P}_i^{''}\cup {P}_i$ is formed and sorted. Finally, the modified replacement strategy is used to generate the next population P $_{i+1}$.

There are two kinds of genetic operators. One kind of genetic operator will be invoked to generate new individuals at a time. In this study, if the generated random number is bigger than the crossover probability p $_c$, the crossover operation will be carried out; otherwise, the mutation operation will be carried out. When the crossover operator is invoked, two different individuals who have never been selected are chosen as parents. Each gene of both parents v $_i$ and v $_j$ is randomly crossed to produce two new individuals c $_i$ and c $_j$. The crossover operation is expressed by Eqs. (19) and (20).

$$\begin{aligned} c_i (k )=0.5\times \{[1+2\times (r_k -0.5)]\cdot v_i (k )+[1-2\times (r_k -0.5)]\cdot v_j (k )\} . \end{aligned}$$

(19)

$$\begin{aligned} c_j (k )=0.5\times \{[1-2\times (r_k -0.5)]\cdot v_i (k )+[1+2\times (r_k -0.5)]\cdot v_j (k )\} . \end{aligned}$$

(20)

where the random number r $_k$ is randomly generated for each gene v(k) of parents. If the mutation operator is applied, just one individual, having never been selected, is chosen as a parent. And each gene of parent v $_i$ plus a random value $\varDelta _k$ is required to generate the new individual c $_i$. The random value $\varDelta _k$ and the mutation operation are expressed by Eqs. (21) and (22) respectively.

$$\begin{aligned} \varDelta _k = 2\cdot (r_k -0.5)\cdot (ub_k -lb_k ) . \end{aligned}$$

(21)

$$\begin{aligned} c_i (k ) = v_i (k )+\varDelta _k . \end{aligned}$$

(22)

where the ub $_k$ is the upper boundary of the gene k and the lb $_k$ is the lower boundary of the gene k.

The stochastic local search operators are applied after the offspring P $_i^{'}$ has been generated by genetic operation. In this search process, both kind of stochastic local search operators work by repositioning the shipboard elements to better satisfy the topological and geometric requirements. Except for the x- and y-coordinates of elements, the remaining five variables are constant during this search process. The stochastic local search operation would not be applied to the individuals with the lowest rank in the population P $_i^{'}$. Since all individuals on the first front of the parent population P $_i$ and offspring population P $_i^{'}$ are included in population Q $_i$, elitism is ensured. The topological operator is used to improve the fitness of individuals. When there is a separation relationship between the two elements E $_i$ and E $_j$, and their spacing D $_{ij}$ is less than the threshold t $_{low}$, the topological operator is invoked. The geometric operator is used to search for arrangements without any overlaps. Hence, the geometric operator would just be invoked if there are overlaps, and in contrast, the topological operator would be used only when there are no overlaps. If either stochastic local search operator is carried out, the elements would be translated to one of eight position, $({x}+\mu ,{y}+\mu ),({x}+\mu ,{y}),({x}+\mu ,{y}-\mu ),({x},{y}+\mu ),({x},{y}-\mu ),({x}-\mu ,{y}+\mu ),({x}-\mu ,{y}),({x}-\mu ,{y}-\mu )$. The magnitude $\mu$ of the translation on x-coordinate direction is randomly calculated between 0 and the length of element, likewise, the magnitude $\mu$ of the translation on y–coordinate direction is randomly calculated between 0 and the width of element. The geometric operator is aimed to reduce the area a $_i$ of overlap and the perimeter p $_i$ reduced the overlap side, expressed by Eqs. (23)–(26). fl $_{ij}$ and fw $_{ij}$ are calculated by Eqs. (8) and (9). pl $_{ij}$ and pw $_{ij}$ are calculated by Eqs. (13) and (14). The topological operator is used to reduce the value of the Separation Function and Adjacency Function. The element will continue to translate until fitness cannot be further reduced.

$$\begin{aligned} a_i = \sum _{j=1}^{N,i\ne j} a_{ij} . \end{aligned}$$

(23)

$$\begin{aligned} a_{ij} = \left\{ \begin{array}{ll} fl_{ij} \cdot fw_{ij} ,&{} fl_{ij}>0\quad and \quad fw_{ij} >0\\ 0,&{} otherwise . \end{array} \right. \end{aligned}$$

(24)

$$\begin{aligned} p_i = \sum _{j=1}^{N,i\ne j} p_{ij} . \end{aligned}$$

(25)

$$\begin{aligned} p_{ij} = 2\times (l_i +w_i )-\sum _{j=1}^{N,i\ne j}(pl_{ij} +pw_{ij} ) . \end{aligned}$$

(26)

The pseudocode for stochastic local search operators is outlined as follows. In this procedure, in order to generate better individuals, the main body (Calculate $\mu$) of this procedure is executed at most 50 times for each individual. When the process is continue to calculate all individuals of population, the total complexity is O(50N).

The pseudocode for stochastic local search operators

3.3 Modified Replacement Strategy

Non-domination rank and crowding distance are two significant attributes of each individual in the NSGA-II. The solution with the lower rank would be retained. If both solutions have the same rank, the solution that is located in a less crowded region would be retained [28]. The crowding distance computation for objectives is used to measure the extent of proximity with other solutions. This guarantees diversity of the population and a uniformly spread out Pareto-optimal front, but the crowding distance computation for objectives is not suitable to maintain the diversity of population for arrangements optimization. In the arrangements optimization problem, two completely different arrangement schemes may have similar values of the objective functions. This means the discrepancy in solution space does not guarantee the differentiability in objective space. The failure to keep diversity of population indicates that the original replacement strategy in the NSGA-II is not sufficient to deal with such problems.

In this paper, a modified replacement strategy is used for the arrangements optimization problem. The position differences of elements are calculated to estimate the diversity of the solution. The quantity d $_{ij}$ serves as a computation of the position difference of all elements between solution i and solution j, determined by Eq. (27).

$$\begin{aligned} d_{ij} = \sum _{k=1}^{N}(|x_k^i -x_k^j |+|y_k^i -y_k^j |) . \end{aligned}$$

(27)

The crowding distance cd $_i$ of the solution i is expressed by Eq. (28), which minimizes the position difference of all elements with other solutions. Hence, the solution with larger crowding distance will be retained in the population if the two solution are on the same non-dominate front. Since each solution must be compared with all other solution in the population, the overall complexity of the crowding distance calculation is O(N $^2$).

$$\begin{aligned} cd_i = min (d_{i1} ,d_{i1} \dots d_{iN} ),\quad i\ne j . \end{aligned}$$

(28)

The pseudocode of the hybrid evolutionary algorithm is outlined as follows. The fast non-dominated sorting approach with O(MN $^2$) computational complexity is presented in [28]. The complexity of this modified replacement strategy is governed by the sorting algorithm. Since K independent sortings of at most N solutions (when all individuals are in one front F) are involved, the modified replacement strategy has O(KNlogN) computational complexity.

The pseudocode of the hybrid evolutionary algorithm

4 A Case Study of a Survey Ship

In this section, a survey ship arrangement optimization was carried out to test whether the proposed algorithm is capable of generating several coherent general arrangements. The shipboard elements involved in the optimization are listed in Fig. 1. Three ship deck spaces considered in the optimization are main deck space S $_1$, accommodation deck space S $_2$ and bridge deck space S $_3$. The z-coordinate z $^i$ and height h $^i$ of elements are constants during the optimization. It is noted that each stair is arranged in the same position on both decks to which it is connected. Also, the submersible decompression chamber is a fixed element during the optimization. The bridge must be arranged in the forefront of bridge deck space. The sizes of the initial population and the offspring are both set as 100. The crossover probability is set as 0.8, and the stopping criterion is set to 500 generations. Finally, four coherent arrangements with some differences were generated as shown in Figs. 2, 3, 4 and 5.

To account for the effectiveness of the stochastic local search operators, the proposed algorithm is run 10 times with and without the stochastic local search operators on each instance. The speed of the two algorithms to find the individuals without any overlaps is shown in Fig. 6. The comparison of the Pareto-optimal fronts with two different replacement strategies is shown in Fig. 7.

The proposed algorithm is run 10 times with original replacement strategy and modified replacement strategy respectively. The number and similarity of solutions in two Pareto-optimal fronts using different replacement strategies is illustrated in Table 2.

Fig. 1.

The color-map of shipboard elements arranged on multi-decks.

Fig. 2.

The arrangement of survey ship (a).

Fig. 3.

The arrangement of survey ship (b).

Fig. 4.

The arrangement of survey ship (c).

Fig. 5.

The arrangement of survey ship (d).

Fig. 6.

The speed of the two algorithms to find the individuals without any overlaps.

Fig. 7.

The comparison of Pareto-optimal fronts with different replacement strategies.

Table 2. The number and similarity of solutions in two Pareto-optimal fronts using different replacement strategies.

5 Discussion

The stochastic local search operators and modified replacement strategy are dis-cussed in this section.

5.1 Stochastic Local Search Operators

The experimental results of stochastic local search operators indicate that these kind of operators are able to facilitate finding the individuals without any overlaps, and improving the performance of the proposed algorithm. The algorithm with the stochastic local search operators is faster to find feasible solutions than the algorithm without the stochastic local search operators. When the stochastic local search operation is carried out, the solutions without any overlaps emerge between 180 and 220 generations. If the stochastic local search operators are not invoked, the solutions without any overlaps would not be able to be discovered, and the number of constraint violations is finally stable at 2–3. However, an algorithm that can rapidly find feasible solutions is expected to result in better optimization.

The Pareto-optimal fronts are also compared. The Adjacency Function and Separation Function are selected as the objective of comparison as shown in Fig. 7. The dashed line zone is composed of black dots that represents the Pareto-optimal solutions generated using the stochastic local search operators. The solid line zone is composed of red dots that represents the Pareto-optimal solutions that does not use the stochastic local search. It can be observed that the dashed line zone is at the bottom left of the solid line zone which means the solution in the dashed line zone is better than in the solid line zone. Thus, it can be concluded that the proposed coupling of the NSGA-II with a stochastic local search technique is able to improve the fitness of solutions, and enhance the performance of searching for a feasible solution.

5.2 Modified Replacement Strategy

The proposed modified replacement strategy is compared with the original replacement strategy in the NSGA-II. The comparison focuses on the number and the similarity of solutions in different Pareto-optimal fronts using the two replacement strategies. As shown in Table 2, the number of solutions in Pareto-optimal fronts using the original replacement strategy is much greater than using the modified replacement strategy. The similarity of solutions using original replacement strategy is 91.3%, and the similarity of solutions using modified replacement strategy is 32.1%. The results indicate that the diversity of population is rapidly lost when the original replacement strategy is used. The original replacement strategy would result in dozens of solutions, but all solutions represent similar arrangements. Furthermore, these solutions are just local optimal solutions. The modified replacement strategy may result in fewer solutions within the Pareto-optimal front, but the Pareto-optimal front contains several different arrangement plans. For instance, there are four different arrangements in the Pareto-optimal front as shown in Sect. 4.

6 Conclusion

This paper investigates the arrangements optimization problems where the size and position of elements are simultaneously considered as optimization variables. The main purpose of this study is to assist ship designers in enhancing the range of alternative arrangements and expediting the design process.

A multi-objective constrained optimization mathematical model of arrangements problem has been established according to the topological and geometrical requirements. The objective functions consist of three evaluators. A series of nonlinear equality constraints is used to determine whether there is overlap between two elements resulting from the constraints of optimization. A survey ship arrangements optimization is applied, and four different general arrangements of the survey ship have been generated.

In order to quickly solve arrangements optimization problems, this paper describes an elitist non-dominated sorting hybrid evolutionary algorithm, in which the NSGA-II is enriched with a stochastic local search technique to tackle the topological and geometrical requirements. It combines the advantages of using an evolutionary algorithm to search a large solution space with a stochastic local search technique to deal with geometrical constraints and locally improve each individual. The modification of the replacement is used to maintain the diversity of population. The effectiveness of both enhancements has been tested. The simulation results indicate that the proposed approach is able to generate a set of coherent arrangements.