Keywords

1 Introduction

Functionally graded materials (FGMs) obtained significant consideration due to outstanding properties, such as high stiffness and strength-to-weight ratios, lightweight, heat-resisting material. On the other hand, FGMs shells have been widely used in aerospace, defense, electronics and nuclear reactors. Therefore, the static and free vibration analysis of FG shells has been receiving considerable concern by researchers. Loy et al. [1] and Pradhan et al. [2] studied the vibration of FG cylindrical shells using the Love’s shell theory. The eigenvalue governing equations are solved by using Rayleigh-Ritz method. However, as the Love’s shell theory neglects the effects of transverse shear, this theory only provides good results for an analysis of the thin shells case. To overcome the drawbacks, the first-order shear deformation theory (FSDT), which accounts for the transverse shear effects, was used to analyze FG shells. Aghdam et al. [3] proposed the extended Kantorovich method (EKM) to solve bending of moderately thick doubly curved FG shells. In this study, they used FSDT and five highly coupled partial differential equation to obtain in term of five displacement components. Su et al. [4] investigated the free vibration of FG cylindrical, conical shells with general boundary conditions using Rayleigh-Ritz method. Using the element-free kp-Ritz method, Zhao et al. [5] investigated the static and vibration of FG shells subjected to mechanical and thermomechanical load based on Sander’s FSDT. Recently, in order to improve the quality of the numerical results, various theories have been developed to analyze FG shell such as the higher-order shear deformation theory (HSDT) [6], layer-wise theory [7]. However, these theories have a high computationally cost which causes the limit of their practical applications. Therefore, from the engineering point of view, the FSDT is still the most attractive and widely used approach due to its simplicity and computational efficiency.

For the purpose of improving the quality of numerical results, Liu and Nguyen [8] proposed a smoothed finite element method (S-FEM), which is based on the stabilized conforming nodal integration (SCNI) of mesh-free method, including the cell-based smoothed finite element (CS-FEM) [9,10,11,12,13], the node-based smoothed finite element [14,15,16], the edge-based smooth finite element method [17, 18] and the face-based smoothed finite element [19]. Each of these S-FEM has different properties and has been successfully introduced for the analysis of practical mechanics problems, especially for various problems plates and shells [20,21,22].

Among these S-FEM models, the CS-FEM shows some interesting properties in the solid mechanics problems. Extending the idea of the CS-FEM to plate structures, Nguyen-Thoi et al. [23] have recently formulated a cell-based smoothed stabilized discrete shear gap element (CS-DSG3) for static and free vibration analyses of isotropic shell structures by combining the CS-FEM with the original DSG3 [24]. In the CS-DSG3, each triangular element will be divided into three sub-triangles, and in each sub-triangle, the stabilized DSG3 is used to compute the strains. Then the strain smoothing technique on whole triangular element is used to smooth the strains on three sub-triangles. The numerical results showed that the CS-DSG3 is free of shear locking and achieves a high accuracy compared with the exact solutions. Recently, the CS-DSG3 has been extended to analyze various plate and shell problems such as flat shells [23], stiffened plates [25], FGM plates [26], piezoelectricity plates [27] and composite plates [28]. However, as far as authors are aware, static and free vibration analysis of FG shells using a CS-DSG3 has not been found yet. Therefore, this paper aims to extend further the CS-DSG3 to static and free vibration analyses of FG shells based on FSDT. The accuracy and reliability of the proposed method are verified by comparing its numerical solutions with those of others available numerical results.

2 Theoretical Formulation

2.1 Functionally Graded (FG) Shells

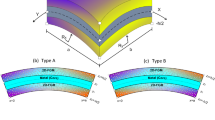
A FG shell made from a mixture of ceramic and metal is shown in Fig. 1. In this study, the material properties are assumed to be graded through the thickness by the power distribution given by

Fig. 1
figure 1

a Geometry of FG doubly curved shell. b Volume fraction of Ceramic (Vc) through the thickness

Full size image
$$ P(z) = (P_{c} - P_{m} )V_{c} + P_{m} ;V_{c} = \left( {\frac{1}{2} + \frac{z}{t}} \right)^{n} \,(n \ge 0) $$
(1)

where P is the effective material properties, including the modulus of elasticity E, density ρ, Poisson’s ratio \( \nu \). P c and P m are the properties of the ceramic and metal, respectively; V c is the volume fraction of the ceramic; t is the thickness of shell and z is the distance from its middle surface; n is the volume fraction exponent which controls the variation of volume fraction through the thickness shown in Fig. 1b.

2.2 Weak Form of FG Shell

According to the first-order shear deformation theory, the displacement field at any point in the shell can be expressed as follows

$$ \left\{ {\begin{array}{*{20}l} {u(x,y,z) = u_{0} (x,y) + z\theta_{x} (x,y),} \hfill \\ {v(x,y,z) = v_{0} (x,y) + z\theta_{y} (x,y)} \hfill \\ {w(x,y,z) = w_{0} (x,y),} \hfill \\ \end{array} } \right., $$
(2)

where \( u_{0} ,v_{0} \) and \( w_{0} \) are the displacements of the mid-plane of shell in x, y and z directions, θ x and θ y donate the rotations around the y- and x-axes, respectively, as shown in Fig. 1a. The generalized strains can be written in terms of the mid-plane deformations, which give

$$ {\varvec{\upvarepsilon}} = \left\{ {\varepsilon_{xx} ,\varepsilon_{yy} ,\gamma_{xy} ,\gamma_{xz} ,\gamma_{yz} } \right\}^{T} = \left\{ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}^{m} } \\ 0 \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\varvec{\upkappa}} \\ 0 \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} 0 \\ {\varvec{\upgamma}} \\ \end{array} } \right\}, $$
(3)

where the membrane strain \( {\varvec{\upvarepsilon}}^{m} , \) bending strain \( {\varvec{\upkappa}} \) and shear strain \( {\varvec{\upgamma}} \) are, respectively, given by

$$ {\varvec{\upvarepsilon}}^{m} = \left\{ {\frac{{\partial u_{0} }}{\partial x},\frac{{\partial v_{0} }}{\partial y},\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}} \right\}^{T} ;{\varvec{\upkappa}} = \left\{ {\frac{{\partial \theta_{x} }}{\partial x},\frac{{\partial \theta_{y} }}{\partial y},\frac{{\partial \theta_{x} }}{\partial y} + \frac{{\partial \theta_{y} }}{\partial x}} \right\}^{T} ;{\varvec{\upgamma}} = \left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\frac{\partial w}{\partial x} + \theta_{x} ,\frac{\partial w}{\partial y} + \theta_{y} } \right\}^{T} . $$
(4)

The linear stress–strain relations are expressed as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{21} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{xx} } \\ {\gamma_{xy} } \\ \end{array} } \right\}; \, \left\{ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{55} } & 0 \\ 0 & {Q_{44} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\}, $$
(5)

where

$$ Q_{11} (z) = Q_{22} (z) = \frac{E(z)}{{1 - \nu (z)^{2} }};\,\, \, Q_{12} (z) = \nu (z)Q_{11} (z); \, Q_{44} (z) = Q_{55} (z) = Q_{66} (z) = \frac{E(z)}{2(1 + \nu (z))}. $$
(6)

The standard Galerkin weak form of the static equilibrium equations for the Reissner-Mindlin shell can be written follow as

$$ \int_{\varOmega } {\delta \left\{ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}^{m} } \\ {\varvec{\upkappa}} \\ {\varvec{\upgamma}} \\ \end{array} } \right\}^{T} \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} & {\mathbf{0}} \\ {\mathbf{B}} & {\mathbf{D}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}^{s} } \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}_{0} } \\ {\varvec{\upkappa}} \\ {\varvec{\upgamma}} \\ \end{array} } \right\}\,d\varOmega = \int_{\varOmega } {\delta {\mathbf{u}}^{T} {\mathbf{b}}} d\varOmega , $$
(7)

where the matrices \( {\mathbf{A}},{\mathbf{B}},{\mathbf{D}} \) and \( {\mathbf{D}}^{s} \) are the extensional, coupling, bending and the transverse shear stiffness, respectively, which are given by

$$ \left( {A_{ij} ,B_{ij} ,D_{ij} } \right) = \int_{ - h/2}^{h/2} {(1,z,z^{2} } )Q_{ij} dz,\,\,\,\,(i,j = 1,2,6); \, D^{s} = \int_{ - h/2}^{h/2} {Q_{ij}^{*} } dz,\,\,\,\,(i,j = 4,5), $$
(8)

And \( {\mathbf{b}} = \left\{ {0,0,p\left( {x,y,z} \right),0,0,0} \right\}^{T} \) is the distributed load applied on the shell.

For the free vibration problems, the standard Galerkin weak form can be expressed by

$$ \int_{\varOmega } {\delta \left\{ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}^{m} } \\ {\varvec{\upkappa}} \\ {\varvec{\upgamma}} \\ \end{array} } \right\}^{T} \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} & {\mathbf{0}} \\ {\mathbf{B}} & {\mathbf{D}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}^{s} } \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}_{0} } \\ {\varvec{\upkappa}} \\ {\varvec{\upgamma}} \\ \end{array} } \right\}\,d\varOmega = \int_{\varOmega } {\delta {\mathbf{u}}^{T} {\mathbf{m}}} {\ddot{\mathbf{u}}} d\varOmega , $$
(9)

where m is the mass matrix containing the mass density of the material \( \rho \).

2.3 The General FEM Formulation of FG Shells

In FEM, the problem domain is discretized using a mesh of n e three-node finite elements such that \( \varOmega = \bigcup\nolimits_{e = 1}^{{n^{e} }} {\varOmega_{{}}^{e} } \) and \( \varOmega^{i} \cap \varOmega^{j} = \emptyset \) for \( i \ne j. \)

The finite element approximation \( {\mathbf{u}}^{h} = \left\{ {u,v,w,\beta_{x} ,\beta_{y} ,\beta_{z} } \right\}^{T} \) of a displacement model for FG shell elements can be expressed as

$$ {\mathbf{u}}^{h} = \sum\limits_{I = 1}^{{N_{n} }} {N_{I} \left( {\mathbf{x}} \right)} {\mathbf{I}}_{6} {\mathbf{d}}_{I} = \sum\limits_{I = 1}^{{N_{n} }} {{\mathbf{N}}_{I} } {\mathbf{d}}_{I} , $$
(10)

where \( {\mathbf{I}}_{6} \) is the unit matrix of sixth rank; \( N_{n} \) is the total number of nodes of problem domain discretized; \( {\mathbf{d}}_{I} = \left\{ {u_{I} ,v_{I} ,w_{I} ,\beta_{xI} ,\beta_{yI} ,\beta_{zI} } \right\}^{T} \) denotes the displacement vector of the nodal degrees of freedom of \( {\mathbf{u}}^{h} \) associated with the Ith node; \( N_{I} \left( {\mathbf{x}} \right) \) is the shape function at the Ith node. According to Eq. (4), the approximation of the membrane, bending and shear strains can be expressed in matrix forms as

$$ {\varvec{\upvarepsilon}}_{0}^{{}} {\mathbf{ = }}\sum\limits_{I} {{\mathbf{R}}_{I}^{{}} {\mathbf{d}}_{I} } ;{\varvec{\upkappa}}{\mathbf{ = }}\sum\limits_{I} {{\mathbf{B}}_{I}^{{}} {\mathbf{d}}_{I} } ;{\varvec{\upgamma}} = \sum\limits_{I} {{\mathbf{S}}_{I}^{{}} {\mathbf{d}}_{I} } , $$
(11)

where

$$ \begin{aligned} {\mathbf{R}}_{I}^{{}} & = \left[ {\begin{array}{*{20}c} {N_{I,x} } & 0 & {0\,\,\,0\,\,\,0\,\,\,0} \\ 0 & {N_{I,y} } & {0\,\,\,0\,\,\,0\,\,\,0} \\ {N_{I,y} } & {N_{I,x} } & {0\,\,\,0\,\,\,0\,\,\,0} \\ \end{array} } \right]{\mathbf{;B}}_{I}^{{}} = \left[ {\begin{array}{*{20}c} {0\,\,\,0\,\,\,0} & {N_{I,x} } & 0 & 0 \\ {0\,\,\,0\,\,\,0} & 0 & {N_{I,y} } & 0 \\ {0\,\,\,0\,\,\,0} & {N_{I,y} } & {N_{I,x} } & 0 \\ \end{array} } \right]; \\ {\mathbf{S}}_{I}^{{}} & = \left[ {\begin{array}{*{20}c} {0\,\,\,0} & {N_{I,x} } & {N_{I} } & 0 & 0 \\ {0\,\,\,0} & {N_{I,y} } & 0 & {N_{I} } & 0 \\ \end{array} } \right]. \\ \end{aligned} $$
(12)

The discretized system of equations of the FG shell for static analysis can be given by

$$ {\mathbf{Kd}} = {\mathbf{F}}, $$
(13)

In which K is the global stiffness matrix which can be computed as

$$ {\mathbf{K}} = \int_{\varOmega } {\left\{ {\begin{array}{*{20}c} {\mathbf{R}} \\ {\mathbf{B}} \\ {\mathbf{S}} \\ \end{array} } \right\}}^{T} \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} & {\mathbf{0}} \\ {\mathbf{B}} & {\mathbf{D}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathbf{R}} \\ {\mathbf{B}} \\ {\mathbf{S}} \\ \end{array} } \right\}d\varOmega , $$
(14)

and F is the global load vector expressed by:

$$ {\mathbf{F}} = \int_{\varOmega } {p{\mathbf{N}}{\text{d}}\varOmega } + {\mathbf{f}}^{b} , $$
(14)

In which \( {\mathbf{f}}^{b} \) is the remaining term of \( {\mathbf{F}} \) subjected to prescribed boundary loads.

For the free vibration analysis problem, we obtained

$$ \left( {{\mathbf{K}} - \omega^{2} {\mathbf{M}}} \right){\mathbf{d}} = {\mathbf{0}}, $$
(15)

where ω is the natural frequency and M is the global mass matrix

$$ {\mathbf{M}} = \int_{\varOmega } {{\mathbf{N}}^{T} {\mathbf{mN}}{\text{d}}\varOmega . \, } $$
(16)

2.4 Brief on the CS-DSG3 Formulation

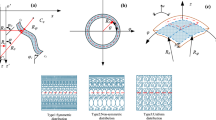
In the DSG3 [24], the shear strain is linear interpolated based on the concept “shear gap” of displacement along the sides of the elements by using the standard element shape functions. Accordingly, the approximation \( {\mathbf{u}}_{e}^{h} \) of a three-node triangular shell element can be written as

$$ {\mathbf{u}}_{e}^{h} = \sum\limits_{I = 1}^{3} {N_{I} \left( {\mathbf{x}} \right)} {\mathbf{I}}_{6} {\mathbf{d}}_{eI} = \sum\limits_{I = 1}^{3} {{\mathbf{N}}_{I} } {\mathbf{d}}_{eI} , $$
(17)

where \( {\mathbf{d}}_{eI}^{h} = \left\{ {u_{I} ,v_{I} ,w_{I} ,\beta_{xI} ,\beta_{yI} ,\beta_{zI} } \right\}^{T} \) is the nodal degrees of freedom of \( {\mathbf{u}}_{e}^{h} \) associated with the Ith node and \( N_{I} \left( {\mathbf{x}} \right) \) is linear shape functions in a natural coordinate defined by

$$ N_{1} = 1 - \xi - \eta ;N_{2} = \xi ;N_{3} = \eta . $$
(18)

Then, the membrane, bending and shear strains in the element are then obtained by

$$ {\varvec{\upvarepsilon}}_{0}^{h} = \left[ {{\mathbf{R}}_{1} ,{\mathbf{R}}_{2} ,{\mathbf{R}}_{3} } \right]{\mathbf{d}}_{e} = {\mathbf{Rd}}_{e} ;{\varvec{\upkappa}}^{h} = \left[ {{\mathbf{B}}_{1} ,{\mathbf{B}}_{2} ,{\mathbf{B}}_{3} } \right]{\mathbf{d}}_{e} = {\mathbf{Rd}}_{e} ;{\varvec{\upgamma}}^{h} = \left[ {{\mathbf{S}}_{1} ,{\mathbf{S}}_{2} ,{\mathbf{S}}_{3} } \right]{\mathbf{d}}_{e} = {\mathbf{Sd}}_{e} , $$
(19)

where

$$ \begin{aligned} {\mathbf{R}}_{1}^{{}} & = \left[ {\begin{array}{*{20}c} {b - c} & 0 & {0000} \\ 0 & {d - a} & {0000} \\ {d - a} & {b - c} & {0000} \\ \end{array} } \right]{\mathbf{;R}}_{2}^{{}} = \left[ {\begin{array}{*{20}c} c & 0 & {0000} \\ 0 & { - d} & {0000} \\ { - d} & c & {0000} \\ \end{array} } \right]; \\ {\mathbf{R}}_{3}^{{}} & = \left[ {\begin{array}{*{20}c} { - b} & 0 & {0000} \\ 0 & a & {0000} \\ a & { - b} & {0000} \\ \end{array} } \right], \\ \end{aligned} $$
(20)
$$ \begin{aligned} {\mathbf{B}}_{1}^{{}} & = \left[ {\begin{array}{*{20}c} {000} & {b - c} & 0 & 0 \\ {000} & 0 & {d - a} & 0 \\ {000} & {d - a} & {b - c} & 0 \\ \end{array} } \right]{\mathbf{;}}\,{\mathbf{B}}_{2}^{{}} = \left[ {\begin{array}{*{20}c} {000} & c & 0 & 0 \\ {000} & 0 & { - d} & 0 \\ {000} & { - d} & c & 0 \\ \end{array} } \right]; \\ {\mathbf{B}}_{3}^{{}} & = \left[ {\begin{array}{*{20}c} {000} & { - b} & 0 & 0 \\ {000} & 0 & a & 0 \\ {000} & a & { - b} & 0 \\ \end{array} } \right], \\ \end{aligned} $$
(21)
$$ \begin{array}{*{20}l} {{\mathbf{S}}_{1}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} {00} & {b - c} & {A_{e} } & 0 & 0 \\ {00} & {d - a} & 0 & {A_{e} } & 0 \\ \end{array} } \right]{\mathbf{;}}\,{\mathbf{S}}_{2}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} {00} & c & {ac/2} & {bc/2} & 0 \\ {00} & { - d} & { - ad/2} & { - bd/2} & 0 \\ \end{array} } \right];} \hfill \\ {{\mathbf{S}}_{3}^{{}} = \frac{1}{{2A_{e} }}\left[ {\begin{array}{*{20}c} {00} & { - b} & { - bd/2} & { - bc/2} & 0 \\ {00} & a & {ad/2} & {ac/2} & 0 \\ \end{array} } \right],} \hfill \\ \end{array} $$
(22)

In which \( a = x_{2} - x_{1} ,b = y_{2} - y_{1} ,c = y_{3} - y_{1} ,d = x_{3} - x_{1} \) with \( {\mathbf{x}}_{i} = \left\{ {x_{i} ,y_{i} } \right\},i = 1,2,3 \) are coordinates of three nodes in the local coordinate system, respectively, as shown in Fig. 2a and \( A_{e} \) denote the area of the triangular element. The global stiffness matrix in Eq. (14) now can be written by:

Fig. 2
figure 2

a Three-node triangular element and local coordinates in the DSG3. b Coordinate transformation in the triangular shell elements. c Three sub-triangles created from the triangle 1-2-3 in CS-DSG3

Full size image
$$ {\mathbf{K}}^{DSG3} = \sum\limits_{e = 1}^{{N_{n} }} {{\mathbf{K}}_{e}^{DSG3} } $$
(23)

where \( {\mathbf{K}}_{e}^{DSG3} \) is the element stiffness matrix of the DSG3 element and is given by:

$$ {\mathbf{K}}_{e}^{DSG3} = {\mathbf{T}}^{T} \left( {\int_{{\varOmega_{e} }} {\left\{ {\begin{array}{*{20}c} {\mathbf{R}} \\ {\mathbf{B}} \\ {\mathbf{S}} \\ \end{array} } \right\}}^{T} \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} & {\mathbf{0}} \\ {\mathbf{B}} & {\mathbf{D}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathbf{R}} \\ {\mathbf{B}} \\ {\mathbf{S}} \\ \end{array} } \right\}d\varOmega } \right){\mathbf{T}}, $$
(24)

with T is the transformation matrix of coordinate from global coordinate xyz to the local coordinate system \( \hat{x}\hat{y}\hat{z} \) [29], as shown in Fig. 2b.

In the formulation of the CS-DSG3 [23, 30], each triangular element is further divided into three sub-triangles by connecting the central point of the element to three field nodes, as shown in Fig. 2c. Then, the displacement vector at central point is assumed to be the simple average of three displacement vectors of three field nodes. In each sub-triangles, the stabilized DSG3 has computed the strains and to avoid the transverse shear locking. Accordingly, the smoothed element membrane strain \( {\tilde{\varvec{\upvarepsilon}}}_{e}^{m} , \) the smoothed element bending strain \( {\tilde{\varvec{\upkappa}}} \) and the smoothed element shear strain \( {\tilde{\varvec{\upgamma}}} \) are written follow as

$$ {\tilde{\varvec{\upvarepsilon}}}_{e}^{m} = {\tilde{\mathbf{R}}}_{e} {\mathbf{d}}_{e} ;\,\,\,\,{\tilde{\varvec{\upkappa}}}_{e}^{{}} = {\tilde{\mathbf{B}}}_{e} {\mathbf{d}}_{e} ;\,\,\,{\tilde{\varvec{\upgamma}}}_{e} = {\tilde{\mathbf{S}}}_{e} {\mathbf{d}}_{e} $$
(26)

where \( {\tilde{\mathbf{R}}}_{e} \), \( {\tilde{\mathbf{B}}}_{e} \) and \( {\tilde{\mathbf{S}}}_{e} \) are the smoothed membrane gradient matrix, smoothed bending gradient matrix and smoothed shear gradient matrix, respectively, given by

$$ {\tilde{\mathbf{R}}}_{e} = \frac{1}{{A_{e} }}\sum\limits_{i = 1}^{3} {A_{{\Delta_{i} }} {\mathbf{R}}_{e}^{{\Delta_{i} }} } ;\,\,\,\,{\tilde{\mathbf{B}}}_{e} = \frac{1}{{A_{e} }}\sum\limits_{i = 1}^{3} {A_{{\Delta_{i} }} {\mathbf{B}}_{e}^{{\Delta_{i} }} } ;\,\,{\tilde{\mathbf{S}}}_{e} = \frac{1}{{A_{e} }}\sum\limits_{i = 1}^{3} {A_{{\Delta_{i} }} {\mathbf{S}}_{e}^{{\Delta_{i} }} } , $$
(25)

where \( A_{\Delta i} \) is the area of sub-triangle \( \Delta_{i} \); \( {\mathbf{R}}_{e}^{{\Delta_{i} }} ,{\mathbf{B}}_{e}^{{\Delta_{i} }} \) and \( {\mathbf{S}}_{e}^{{\Delta_{i} }} \) are, respectively, the membrane, bending and shear strain gradient matrices of sub-triangle \( \Delta_{i} \). Substituting matrix \( {\tilde{\mathbf{R}}}_{e} ,\,\,{\tilde{\mathbf{B}}}_{e} \,{\text{and}}\,\,{\tilde{\mathbf{S}}}_{e} \) in Eq. (26) into Eq. (14), the global stiffness matrix of CS-DSG3 element is obtained by

$$ {\mathbf{K}}_{e}^{CS - DSG3} = {\mathbf{T}}^{T} \left( {\int_{{\varOmega_{e} }} {\left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{R}}}_{e} } \\ {{\tilde{\mathbf{B}}}_{e} } \\ {{\tilde{\mathbf{S}}}_{e} } \\ \end{array} } \right\}}^{T} \left[ {\begin{array}{*{20}c} {\mathbf{A}} & {\mathbf{B}} & {\mathbf{0}} \\ {\mathbf{B}} & {\mathbf{D}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} & {{\mathbf{D}}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{R}}}_{e} } \\ {{\tilde{\mathbf{B}}}_{e} } \\ {{\tilde{\mathbf{S}}}_{e} } \\ \end{array} } \right\}d\varOmega } \right){\mathbf{T}}, $$
(27)

From Eqs. (26) and (27), we can see that the values of element stiffness matrix at the drilling degree of freedom \( \beta_{z} \) equal zero which can cause the singularity in the global stiffness matrix when all the element meeting at node are coplanar. To solve this problem, the null values of the stiffness corresponding to the drilling degree of freedom are replaced by approximate values. This approximate value is taken to be equal to \( 10^{ - 3} \) times the maximum diagonal value in the element stiffness matrix [23].

3 Numerical Results

In this section, various numerical examples are presented to show the accuracy and stability of the CS-DSG3 for static and free vibration responses of FG shells. The results are compared to the other existing numerical solutions. The central normalized deflection and non-dimensional fundamental frequencies is given by

$$ \bar{w} = \frac{{E_{c} h^{3} }}{{qa^{4} }}w;\bar{\Omega } = \omega h\sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-0pt} {E_{c} }}} . $$
(26)

The first example, consider a fully clamped spherical FG shell under uniformly distributed load. Geometrical parameters for spherical shell are: \( a/b = 1,R_{x} = R_{y} = R, \) length-to-thickness ratio \( a/h = 10 \) and radius-to-length ratios \( R/a = 5,10. \) Mechanical properties of metal (SUS-304): \( E_{m} = 207.79\,\text{GPa},\) \( \nu_{m} = 0.32 \) and ceramic (Si3N4): \( E_{c} = 322.27\,\text{GPa},\) \( \nu_{c} = 0.24 \). The volume fraction exponent (n) is variable. The results of the central normalized deflection are presented and compared with Aghdam et al. [3]. It is found that the results presented in Table 1 are in excellent agreement with above-published results.

Table 1 Comparison of the central normalized deflection of FG spherical shell
Full size table

This example is further extended for static analysis of FG spherical shell when the change in volume fraction exponent and the radius-to-length ratios are shown in Table  2.

Table 2 Central normalized deflections of FG spherical shell with various radius-to-length ratio (R/a) and the volume fraction exponent (n)
Full size table

The next example, consider a fully clamped cylindrical FG shell subjected to uniformly distributed load. Geometrical parameters for cylindrical shell are: a/b = 1, R x  = R, \( R_{y} = \infty \), radius-to-length ratio \( R/a = 2 \) and length-to-thickness ratio \( a/h = 10 \) Mechanical properties are metal (Aluminum): \( E_{m} = 70\,\text{GPa},\nu_{m} = 0.3 \) and Ceramic (SiC): \( E_{c} = 427\,\text{GPa},\nu_{c} = 0.17. \) The volume fraction exponent n is equal to 2. The results for the central normalized deflection along the x-axis are shown in Table 3 and compared with Aghdam et al. [3] and ABAQUS. The present results are in close agreement with EKM and ABAQUS.

Table 3 Comparison of the central normalized deflection (27) of cylindrical FG shell along x-axis
Full size table

Table 4 presents the responses of FG cylindrical shell with different volume fraction exponent and radius-to-length ratios. From Tables 3 and 4, it is found that the behavior of FG shallow shells become softening when the volume fraction exponent (n) increase from ceramic to metal. Furthermore, the increase of curvature ratio leads to increasing displacement of FG shallow shells.

Table 4 Non-dimensional center deflections 10 of FG cylindrical shell with various radius-to-length ratio (R/a) and the volume fraction exponent (n)
Full size table

Finally, the vibration of simply supported FG plate and three types of shallow shell include spherical, cylindrical and hyperbolic paraboloid is investigated. Geometrical parameters for plate are \( a/b = 1 \), length-to-thickness ratio \( a/h = 10 \) and shallow shell are \( a/b = 1 \), radius-to-length ratio \( R/a = 2 \), length-to-thickness ratio \( a/h = 10 \). The volume fraction exponents n = 0, 0.5, 1, 4 and 10 are considered. Mechanical properties are metal (Aluminum): \( E_{m} = 70\,\text{GPa}, \) \( \nu_{m} = 0.3, \) \( \rho = 2700\,\text{kg/m}^{3} \) and Ceramic (Alumina): \( E_{c} = 380\,\text{GPa},\,\,\,\,\nu_{c} = 0.3,\,\,\rho = 3800\,\text{kg/m}^{3} . \) Table  5 shows results with coarse mesh size 8 × 8. It is found that numerical results are in excellent agreement with results available of Alijani et al. [31], Matsunaga [32] and Chorfi and Houmat [33].

Table 5 Non-dimensional fundamental frequencies of FG plate and three types FG shallow shells
Full size table

4 Conclusions

In the present study, a combination of the cell based on smoothed discrete shear gap method with three-node triangular elements is proposed to investigate the static responses and free vibration of FG shells include spherical, cylindrical and hyperboloid paraboloid shells. The first-order shear deformation theory is used in the formulation due to the simplicity and computational efficiency. The effects of several parameters such as the radius-to-length ratios and the volume fraction exponent are examined. Present results are in good agreement in most of the cases which are compared with reference solutions.