Non-cooperative Monomino Games

Abstract

In this paper we study monomino games. These are two player games played on a rectangular board with R rows and C columns. The game pieces are monominoes, which cover exactly one cell of the board. One by one each player selects a column of the board, and places a monomino in the lowest uncovered cell. This generates a payoff for the player. The game ends if all cells are covered by monominoes. The goal of each player is to place his monominoes in such a way that his total payoff is maximized. We derive the equilibrium play and corresponding payoffs for the players.

We thank the Editor and two anonymous reviewers for their helpful comments.

1 Introduction

In this paper we introduce the two-player game of monomino. This is a parlor game like dice games, card games and so on. Instead of determining the player that makes the last move (like in chess, checkers, or the game of Nim), the players are interested in optimizing their payoffs (like in dice games and card games). This game is played on a rectangular board or grid, say it has size $3\times 3$. The cells on the bottom (first) row have a value of 1 unit each, on the middle (second) row the values are 2, and on the top (third) row the cells have a value of 3 units each. The players alternately play a monomino, which is a piece that covers a single cell of the board.

This game has the following rules. The players select one by one a column of the board, and place a monomino in the lowest uncovered cell. A monomino in row i on the board generates a payoff of i units to the player. The game ends if all cells are covered by monominoes. In contrast to games like chess and checkers, the goal of each player is to place his monominoes in such a way that it maximizes his total payoff.

In this paper we analyze non-cooperative monomino games for general rectangular boards. Notice that the game looks a bit like the game of Tetris but it is played with monominoes. More general, it resembles a combinatorial game; both have two players, complete information, and no chance involved. The main difference is that we are interested in optimizing the payoffs of the players, instead of determining who makes the last move. The latter question is not interesting in this game since the winner may be determined beforehand. For instance, if the player who plays the last monomino wins, then the winner is determined as follows. If the number of cells is odd, then the player who makes the first move wins, and if the number of cells is even, then the player who makes the second move wins.

In the literature on combinatorial games the focus is on how to win games with dominoes or other pieces like pentominoes. [8] studies winning moves for the game of pentominoes. [6] describes a two-player game played on a square board. One by one the players mark a cell on the board. The first player to form a domino loses; hence the game is named dominono. The author provides winning strategies. Tilings with polyominoes are studied in [10]. Excellent surveys on combinatorial games are [1, 5]. In cooperative game theory, attention is also paid to combinatorial games; see [2] for a survey.

The literature on non-cooperative game theory pays among others attention to parlor games like dice games [3], matching pennies, rock-paper-scissors, and two-finger Morra (see e.g. [9]). These are zero-sum games, that is, the gain of one player is the loss of the other player. Also, nearly always these games have no equilibrium in pure strategies.

In this paper we introduce monomino games and study them using non-cooperative game theory. Our results describe the equilibrium play and payoffs for the players. The monomino game is a constant sum game and thus has a Nash equilibrium in pure strategies. An initial study on monomino games is reported in the thesis [4].

The outline of this paper is as follows. In Sect. 2 we introduce monomino games. In Sect. 3 the equilibrium play and payoffs are considered. Section 4 concludes.

2 Monomino Games

A monomino game is played by two players on a rectangular board with R rows and C columns. We denote such a monomino game by M(R, C). Each of the RC cells is square. The game is played with pieces of $1\times 1$ cell; these pieces are named monominoes.

The players are named player 1 and player 2. Player 1 starts. One by one the players put a monomino on the board according to the following rules. A monomino is placed in a cell of the board. If the piece is placed in column i of the board, then this monomino covers the lowest uncovered cell. The game ends if all cells are covered by monominoes; this happens after RC moves.

Each played monomino generates a value for its player. If a player places a monomino in row j then this increases the payoff of this player by j units. Each player wants to maximize his payoff. Hence, this game is a non-cooperative game. The Nash equilibrium [7] is a solution concept for non-cooperative games that describes optimal play of the game. Namely, a pair of strategies $(s_1,s_2)$ for the players is a Nash equilibrium if $s_1$ optimizes player 1’s payoff in case player 2 plays strategy $s_2$, and conversely, $s_2$ optimizes player 2’s payoff in case player 1 plays strategy $s_1$. For a game in extensive form we consider subgame perfect equilibria, a refinement of Nash equilibria. A subgame perfect equilibrium is a pair of strategies that induces a Nash equilibrium in every subgame. These notions are illustrated in the example below.

Example 1

Consider the game M(3, 2). This game is played on a board with three rows and two columns. After six moves all six cells on the board are covered and the game is over.

This game already has very many possible plays. To be able to represent the game graphically, assume just for the remainder of this example that if a player can choose among both cells in the same row, then the player selects the cell in column 1.

Figure 1 shows a graphical representation of this game as a game in extensive form, or tree game. At each node of this tree we mention the player that makes a move as well as the game situation $[x_1,x_2]$ with $x_i$ the number of covered cells in column i. The actions are mentioned besides the edges, with $V_i$ the action that column i is selected. At the bottom nodes the payoffs $(\pi _1,\pi _2)$, with payoff $\pi _j$ to player j, are mentioned.

Fig. 1.

The game M(2, 3) in extensive form with the extra restriction that if a player can choose among both cells in the same row, then the player selects the cell in column 1. (Color figure online)

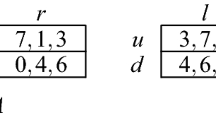
At the first node, player 1 makes the move. According to the extra assumption in this example she has only one action, namely $V_1$ (select column 1). In the new game situation [1, 0] player 2 can choose between $V_1$ and $V_2$. And so on. We find the optimal payoffs and actions by using backward induction. The optimal actions are indicated by thick colored lines; red corresponds to player 1 and blue to player 2. There is a unique subgame perfect equilibrium, that is presented in Table 1. Notice that any subgame corresponds to a game situation. The equilibrium payoff is $(\pi _1,\pi _2)=(5,7)$. The equilibrium play is as follows.

Table 1. The subgame perfect equilibrium in Fig. 1.

Player 1 starts in game situation [0, 0] with action $V_1$, then the new game situation is [1, 0] and player 2 plays $V_2$. Subsequently, player 1 plays $V_1$, and so on. See Table 1 or the thick lines in Fig. 1.

The bimatrix game that corresponds to this game in extensive form is presented below. The actions of player 1, represented by the rows of the bimatrix, correspond to the nontrivial choices in the game situation [2, 0]. The actions of player 2, mentioned in the columns of the bimatrix, are denoted by a|bc with a the choice in situation [1, 0], b the choice in situation [2, 1] if the previous situation was [2, 0], and c the choice in situation [2, 1] if the previous situation was [1, 1].

The two Nash equilibria are $(V_1,V_2|V_1V_1)$ and $(V_1,V_2|V_2V_1)$; they are indicated by stars in the bimatrix. The first one is the subgame perfect equilibrium.  $\Box$

In the example above we temporarily added the restriction that a player should select a cell in column 1 when both cells are available in the same row. Even with this assumption, the game tree is not small. In this paper we consider games without this assumption, leading to even larger game trees.

Given a monomino game M(R, C), the total payoff to the players is fixed, namely $C(1+2+\ldots +R)=CR(R+1)/2$. Any payoff $(\pi _1,\pi _2)$ satisfies $\pi _1+\pi _2=CR(R+1)/2$. Thus, monomino games are constant sum games. This implies in particular that there exists a Nash equilibrium in pure strategies [9]. Further, if there are multiple Nash equilibria, then the payoff to a player is the same in all equilibria. This was illustrated in Example 1.

3 Game Play and Payoffs in Equilibrium

In this section we analyse the monomino games. We derive the optimal game play and the payoffs in equilibrium.

The following notation is used. The cells of the grid are indicated by pairs (i, j), where $1 \le i \le R$ is the row number and $1 \le j \le C$ the column number. Let $\mathcal{R} = \{0,1,2, \ldots , R\}$ be the set of the number of possible unoccupied cells per column. We consider vectors $\mathrm{\mathbf{p}}= (p_1,p_2, \ldots , p_C) \in \mathcal{R}^C$ and denote $P=\sum _{j=1}^C p_j$. The vector $\mathrm{\mathbf{p}}$ describes for any column j, $1 \le j \le C$, that the cells 1 up to $R - p_j$ are occupied with monominoes and the top $p_j$ cells are free. In other words, the vector $\mathrm{\mathbf{p}}$ represents a position on the playing board when $RC - P$ monominoes have been played.

The following Theorem states the equilibrium, or optimal, actions for the players. The equilibrium payoffs are mentioned in Corollary 3.

Theorem 2

In the monomino game M(R, C), the game play in equilibrium is as follows.

• (a) If R is even:

  In each move, player 2 plays the same column as player 1.

• (b) If R is odd and C is even:

  Player 2 plays row 1 if player 1 does so, otherwise he plays the same column as player 1.

• (c) If both R and C are odd:

  Player 1 plays row 1 in his first move. Thereafter he plays row 1 if player 2 does so, otherwise he plays the same column as player 2.

Proof

The theorem is proved by induction to the number of remaining moves if started from a certain position $\mathrm{\mathbf{p}}$. That is, we focus on the payoffs for the players for occupying the remaining free cells if started at position $\mathrm{\mathbf{p}}$ (independent of who placed the monominoes where in the starting position $\mathrm{\mathbf{p}}$).

First, consider case (a). We prove that this play is optimal with respect to the remaining payoffs for each starting position $\mathrm{\mathbf{p}}\in \mathcal{R}^C$, where $p_j$ is even for all $1 \le j \le C$. Hence it is also optimal for an empty grid in case R is even.

We use induction to $n = P/2$, the number of moves remaining for player 2 until all cells of the grid are occupied. The induction basis for $n = 1$ is trivial: in the starting position only the two top cells of one column are free and so both players must play this column.

Now let $n \ge 1$ and suppose that the play is optimal for all starting positions $\mathrm{\mathbf{p}}$ satisfying $p_j$ even for all $1 \le j \le C$ and $P/2 = n$. Consider a starting position $\mathrm{\mathbf{q}}\in \mathcal{R}^C$ with $q_j$ even for all $1 \le j \le C$ and $Q/2 = n + 1$. Since an even number of cells is occupied, it is player 1’s turn. Suppose player 1 plays column k, i.e., cell $(R-q_k+1,k)$ and player 2 plays column $\ell \ne k$; i.e. cell $(R-q_{\ell }+1,\ell )$. Now player 1 can play cell $(R-q_{\ell }+2, \ell )$ in his next move (because $q_{\ell }$ is even). This results in a position that is equivalent to the situation where player 1 plays column k in starting position $\mathrm{\mathbf{p}}= (q_1, \ldots , q_{\ell } - 2, \ldots , q_C)$.

Note that $\mathrm{\mathbf{p}}$ satisfies the conditions of the induction hypothesis, so player 2 will now play the same column as player 1 until the end of the game in order to maximize his remaining payoff (and will therefore play column k in his next move).

Now we compare this with the situation where player 2 had played column k after player 1 played this column in position $\mathrm{\mathbf{q}}$. In this case the position $(q_1, \ldots , q_k - 2, \ldots , q_C)$ arises, which also satisfies the conditions in the induction hypothesis. So player 2 would then continue with the optimal play, i.e., playing the same column as player 1 until the end of the game.

Consequently, the final position of the pieces on the board at the end of the game only differs in the cells $( R-q_{\ell }+1,\ell )$, which is now occupied by a monomino of player 2 and $(R-q_{\ell }+2,\ell )$, occupied by a monomino of player 1. Therefore the remaining payoff for player 2’s moves from position $\mathrm{\mathbf{q}}$ until the end of the game, will be one unit less than the payoff he would have gotten if he had played the same column as player 1 in position $\mathrm{\mathbf{q}}$, as the play prescribes. Hence, the play is optimal for starting position $\mathrm{\mathbf{q}}$ for player 2 regardless of what player 1 does. Now the proof follows by induction.

Second, consider case (b). Let $\mathrm{\mathbf{p}}\in \mathcal{R}^C$ be a starting position on the grid for which the number of nonempty columns is even and each of these columns has an even number of free cells (also fully occupied columns are considered to have an even number of free cells). Obviously, the position on an empty grid satisfies this property: for an empty grid the number of nonempty columns equals zero.

Clearly, P is even for these positions. Again we use induction to $n = P/2$. The induction basis for $n = 1$ is easily verified because in that case there are essentially two possible starting positions: the two top cells of one column are free and so both players must play this column, or $R = 1$, which is also trivial.

Now let $n \ge 1$ and suppose that the play is optimal for all starting positions $\mathrm{\mathbf{p}}$ satisfying $P/2 = n$ and the number of nonempty columns is even and each of these columns has an even number of free cells. Consider a starting position $\mathrm{\mathbf{q}}\in \mathcal{R}^C$ with $Q/2 = n + 1$ satisfying this property. Note that the number of occupied cells in $\mathrm{\mathbf{q}}$, $RC - Q$, is even. Hence, it is player 1’s turn. We will distinguish three cases.

Case b1: Player 1 plays row 1, say cell (1, k), and player 2 does not, say he plays the nonempty column j, i.e., cell $(R-q_j+1,j)$. Then, in his next move, player 1 can play cell $(R-q_j+2,j)$ (because $q_j$ is even). This yields a position that also arises from position $\mathrm{\mathbf{p}}= (q_1, \ldots , q_j-2 , \ldots ,q_C)$ if player 1 plays cell (1, k). Note that $\mathrm{\mathbf{p}}$ satisfies the conditions in the induction hypothesis, so player 2 can optimize his remaining payoff in position $\mathrm{\mathbf{p}}$ by using the play described above (starting by playing row 1). Now we compare this with the situation where player 2 had played row 1 after player 1 played this row in position $\mathrm{\mathbf{q}}$. Then the position that arises again satisfies the conditions in the induction hypothesis. So player 2 would continue by playing the optimal play until the end of the game.

We find that the remaining payoff for player 2 in position $\mathrm{\mathbf{q}}$ will be one unit less than the payoff he would have gotten if he had played row 1, as the play prescribes (the ownership of the cells $(R-q_j+1,j)$ and $(R-q_j+2,j)$ is interchanged).

Case b2: Player 1 plays nonempty column j (cell $(R-q_j+1,j)$) and player 2 plays nonempty column $k \ne j$ (cell $(R-q_k+1,k)$). Now player 1 can play cell $(R-q_k+2,k)$ in his next move and we arrive in a position that is equivalent to the situation where player 1 plays column j in starting position $\mathrm{\mathbf{p}}= (q_1, \ldots , q_k-2, \ldots ,q_C)$. By the induction hypothesis, player 2 can optimize his remaining payoff in this position by using the play described above (starting by playing column j). Again we derive that player 2’s remaining payoff in position $\mathrm{\mathbf{q}}$ will be one unit less than if he had started by playing column j, as the play prescribes.

Case b3: Player 1 plays nonempty column j (cell $(R-q_j+1,j)$) and player 2 plays row 1, say cell (1, k). Then, in his next move, player 1 can play column j again (cell $(R-q_j+2,j)$). If we now interchange the ownership of the monominoes in cells $(R-q_j+2,j)$ and (1, k), we arrive in a position that is equivalent to the situation where player 1 plays cell (1, k) in starting position $\mathrm{\mathbf{p}}= (q_1, \ldots , q_j-2 , \ldots ,q_C)$ (here we use the fact that the remaining payoffs in a starting position are independent of how this position has arisen). By the induction hypothesis, player 2 can optimize his remaining payoff in position $\mathrm{\mathbf{p}}$ by using the play described above (starting by playing row 1). If we compare this with the situation where player 2 had played column j in position $\mathrm{\mathbf{q}}$ and thereafter followed the (by the induction hypothesis optimal) play in position $(q_1, \ldots , q_j-2 , \ldots ,q_C)$, we find that the remaining payoff for player 2 in position $\mathrm{\mathbf{q}}$ will be $R-q_j+1$ units less than if he had started by playing column j, as the play prescribes.

In all three cases the play turns out to be optimal for position $\mathrm{\mathbf{q}}$ no matter what player 1 does. Also here, the proof follows by induction.

Finally, consider case (c). Let $\mathrm{\mathbf{p}}\in \mathcal{R}^C$ be a starting position on the grid for which the number of nonempty columns is odd and each of these columns has an even number of free cells (also fully occupied columns are considered to have an even number of free cells). Clearly, such a position arises as soon as player 1 played his first move. The proof now follows the same lines as the proof of part (b) with reversed roles for players 1 and 2, and an induction hypothesis for positions with an odd number of nonempty columns, all containing an even number of free cells. Finally, since player 1 must play row 1 in his first move, we conclude that the play described in part (c) of the theorem is the equilibrium play for grids with an odd number of rows and columns. $\Box$

Figure 2 shows the optimal game play and payoffs of the monomino games M(6, 4), M(5, 4) and M(5, 5), which correspond to the cases (a), (b) and (c) respectively in Theorem 2. Row 1 is the bottom row, and row R the top row. The number in a cell indicates which player puts a monomino there. The optimal payoffs $(\pi _1,\pi _2)$ are (36, 48), (26, 34) and (43, 32) from left to right.

Fig. 2.

Optimal game play in monomino games M(6, 4), M(5, 4) and M(5, 5) from left to right with optimal payoffs (36, 48), (26, 34) and (43, 32), respectively. The number in a cell indicates which player puts a monomino there.

The equilibrium payoffs to the players are easy to derive following the game play described in Theorem 2, and illustrated in Fig. 2. In case (a), player 2 forces his monominoes to occupy all cells in the even rows of the grid and player 1’s monominoes occupy the odd rows. In case (b) the monominoes of player 2 will occupy half of the cells in row 1 and all cells in the other odd rows, whereas player 1’s monominoes will occupy the other cells in the first row and all cells in the even rows. In case (c), player 1 forces his monominoes to occupy $\frac{C+1}{2}$ cells in row 1 and all cells in the other odd rows, and player 2’s monominoes will occupy the other cells in the first row and all cells in the even rows. From this, the derivation of the payoffs to the players is straightforward, using $\sum _{k=1}^R k = \frac{1}{2} R(R+1)$.

Corollary 3

The optimal payoffs in the monomino game M(R, C) are as follows.

$$ (\pi _1,\pi _2) = \left\{ \begin{array}{ll} \left( \frac{CR^2}{4},\frac{CR(R + 2)}{4}\right) , &{} if ~R~ is~ even,\\ \left( \frac{C(R^2 + 1)}{4},\frac{C(R^2 + 2R - 1)}{4}\right) , &{} if~R~is~odd~and~C~even, \\ \left( \frac{CR(R + 2) - C + 2}{4},\frac{C(R^2 + 1) - 2}{4}\right) , &{} if~ R ~and~ C~ odd. \end{array} \right. $$

4 Conclusions

In this paper we introduced a new class of non-cooperative games: the monomino games M(R, C). These are parlor games like dice games, card games and so on. Instead of determining the player that makes the last move (like in chess, checkers, or the game of Nim), the players are interested in optimizing their individual payoffs (like in dice games and card games). These are constant sum games, so Nash equilibria in pure strategies exist. We derived the equilibrium game play and the corresponding payoffs for any size of the board of the game.

Note that the results for game play and corresponding payoffs in Theorem 2 and Corollary 3 can easily be generalized to games with pieces or playing blocks of size $k \times 1$, for any positive integer k, and playing boards of size $kR \times C$ where the blocks must be played vertically. That is, any block is placed in a single column.

For future research, we intend to study non-cooperative ‘domino’ games. These games are also played on a rectangular board where players one by one put pieces of size $1\times d$ on the board either in horizontal or vertical direction. (For $d=2$ the pieces are the well-known domino pieces.) Some initial analysis of these games is done in [4]. There it turned out that these games are much more complex than monomino games. One of the reasons is that in these domino games some cells of the board may remain uncovered.

Finally, in this paper we consider monomino games with two players. It might also be interesting to examine equilibrium game play in case more than two players are involved.