An Improved Particle Filter Algorithm Based on Swarm Intelligence Optimization

Abstract

Due to the problem of particle degeneracy and loss of particle diversity in particle filter algorithm, this paper proposes an improved particle filter algorithm referring to some ideas of optimized algorithm like particle swarm and firefly group. The proposed algorithm utilizes the firefly algorithm to optimize particle filter and avoid re-sampling process; makes the particles move towards the location of better weight particles and prevents the small weight particles from disappearing after several iterations. Meanwhile, this algorithm sets a transition threshold and iteration times in order to improve the real-time property of the algorithm. Experimental results show that the improved algorithm possesses higher estimation accuracy and keeps good diversity of particle.

1 Introduction

Particle filter is a recursive Bayesian estimation method based on Monte-Carlo simulation. As it possesses the advantages of applying to nonlinear and non-Gaussian noise, particle filter is widely used in various fields including visual tracking, robot localization, aerial navigation and process fault diagnosis. Its main idea is to get a set of random sample spreading in the state space to make approximation of probability density function and replace integral operation with sample means, in order to get the minimum variance distribution of state.

In the process of practical application, the major problem of particle filter is that after several iterations, the importance weight may focus on minority particles. But these particles could not express the posterior probability density function accurately, namely particle degeneracy. To the problem of particle degeneracy, re-sampling method could be adopted. However, re-sampling algorithm duplicate large weight samples and abandon small ones, which could leads to the impoverishment of particles. And to the problem of particle impoverishment, scholars form in and abroad have made a great deal of researches. The method of local re-sampling was proposed in [1]. Its basic idea is separating the particles into three particle assemblies—high, mid, low according to weight degrees, abandoning the lower weights, maintain the middle weights and duplicate the higher ones. The particle filters chosen based on weights was also mentioned in [2]. This method selects a certain number of particles with higher weight form a whole collection of particles to be used in state estimation at net time. Also, deterministic re-sampling particle filter algorithm was proposed in [3] which could avoid abandoning those lower weight ones directly and maintain particle diversity to a degree. However, all these methods mentioned above are still based on traditional frame of re-sampling. The problem of particle impoverishment is still not solved thoroughly.

At present, particle filter based on swarm intelligence optimization [4] is an important developing orientation in the area of particle filter theory. It could regard the particles as individuals of biotic community and simulate their acting regulations [5] to make particle distribution more reasonable. These kinds of method improve the re-sampling steps and do not abandon low weights particles, thus being able to solve impoverishment problems. Particle filter based on swarm optimization [6] is a representative of intelligence optimized particle filters. Particle filter algorithm based on self-adapted particle swarm optimization was proposed in [7]. It could control the quantity of particles from neighborhood self-adaptively, thus improving the reasonability of sample distribution and accuracy of filter. The method of optimizing particle filters based on ant group algorithm was put forward in [8]. It could make the lower weight particles move toward higher likelihood areas and make the particles have better posterior probability distribution. Particle filter algorithm based on artificial firefly swarm optimization was proposed in [9], which only uses its particle transfer formula to recombine the sample instead of iterations.

Considering the problems mentioned above, this research makes improvements on the location of firefly algorithm [10] and brightness update formula. With reference to particle swarm algorithm [11], the study utilizes global optimum to guide the integral movements of particle swarms, comes up with a simplified brightness formula to find best particle, pre-treats the particle groups, successfully combines firefly group optimization method with particle filer. This method avoids more operation complexity brought by particle interaction and meanwhile, improves the precision of particle filter greatly.

2 Basic Particle Filter

Particle filter is a kind of estimation method of Monte-Carlo simulation based on Bayesian estimation. It focuses on solving state estimation problems of dynamic random system. Assume that the dynamic process of nonlinear system is as follows:

$$ x_{t} = f\left( {x_{t - 1} ,u_{t - 1} } \right) $$

(1)

$$ y_{t} = h\left( {x_{t} ,n_{t} } \right) $$

(2)

$x_{t}$ is status value, $y_{t}$ is observed value, $f\left( * \right)$ is state transition function, $h\left( * \right)$ is observation function, $u_{t - 1}$ is system noise, $n_{t}$ is observational noise.

State prediction equation is

$$ p\left( {\left. {x_{t} } \right|y_{1:t - 1} } \right) = \int {p\left( {\left. {x_{t} } \right|x_{t - 1} } \right)} \left. {p\left( {\left. {x_{t - 1} } \right|y_{1:t - 1} } \right)} \right|dx_{t - 1} $$

(3)

Update equation is

$$ p\left( {\left. {x_{t} } \right|y_{1:t} } \right) = \frac{{p\left( {\left. {y_{t} } \right|x_{t} } \right)p\left( {\left. {x_{t} } \right|y_{1:t - 1} } \right)}}{{p\left( {\left. {y_{t} } \right|y_{1:t - 1} } \right)}} $$

(4)

$p\left( {\left. {y_{t} } \right|y_{1:t - 1} } \right) = \int {p\left( {\left. {y_{t} } \right|x_{t} } \right)p\left( {\left. {x_{t} } \right|y_{1:t - 1} } \right)dx_{t} }$ is normalization constant.

General steps are as follows:

• Step 1: Initialization of Particles. Particle assembly $\left\{ {x_{0}^{i} ,i = 1,2, \ldots ,N} \right\}$ is generated by prior probability $p\left( {\left. {x_{0} } \right|y_{0} } \right) = p\left( {x_{0} } \right)$, weight of all particles is 1/N.

• Step 2: Importance function known and easy to be sampled is

  $$ q\left( {\left. {x_{0:t} } \right|y_{1:t} } \right) = q\left( {x_{0} } \right)\prod\nolimits_{j = 1}^{t} {q\left( {\left. {x_{j} } \right|x_{0:j - 1} ,y_{1:j} } \right)} $$

  (5)

  At this time, particle assembly is $\left\{ {\tilde{x}_{t}^{i} } \right\}_{i = 1}^{N}$

• Step 3: Calculating Particle Weight

  $$ w_{t}^{i} = \frac{{p\left( {\left. {y_{1:t} } \right|x_{0:t} } \right)p\left( {x_{0:t} } \right)}}{{q\left( {\left. {\widetilde{{x_{t} }}} \right|x_{0:t - 1} ,y_{1:t} } \right)q\left( {x_{0:t - 1} ,y_{1:t} } \right)}} = w_{t - 1}^{i} \frac{{p\left( {\left. {y_{t} } \right|\tilde{x}_{t} } \right)p\left( {\left. {\tilde{x}_{t} } \right|x_{t - 1} } \right)}}{{q\left( {\left. {\tilde{x}_{t} } \right|x_{t - 1} ,y_{t} } \right)}} $$

  (6)

• Step 4: Normalization of Weight

  $$ w_{t}^{i} = w_{t}^{i} /\sum\nolimits_{i = 1}^{N} {w_{t}^{i} } $$

  (7)

• Step 5: Re-sampling

  Do re-sampling of particle assembly $\left\{ {\tilde{x}_{t}^{i} ,w_{t}^{i} } \right\}$ at this moment, then the particle assembly turns into $\left\{ {x_{t}^{i} ,1/N} \right\}$; The weight of each particle is 1/N, preparing for the next cycling calculation.

• Step 6. Output. The state value of time t is

  $$ \widetilde{{x_{t} }} = \sum\nolimits_{i = 1}^{N} {\widetilde{x}_{t}^{i} w_{t}^{i} } $$

  (8)

Then the algorithm turns back to Step 2 and does cycling operation in order to realize cycling tracking of systematic state.

3 Particle Swarm Optimization Firefly Algorithm -PF Algorithm (PSOFA-PF)

In order to overcome the defects of common particle filter, this paper introduces the idea of particle swarm and firefly algorithm into particle filter to improve the optimization process. As there exist similarities between these two algorithms and particle filter, they could be combined to get more effective particle filter algorithm.

3.1 Particle Swarm Optimization and Firefly Algorithm

The basic principle of PSO: Initialize a particle swarm randomly which contains particles with the quantity of m, dimension of n. The location of particle I is $X_{i} = \left( {x_{i1} ,x_{i2} , \ldots ,x_{in} } \right)$, speed $V_{i} = \left( {v_{i1} ,v_{i2} , \ldots ,v_{in} } \right)$. In the process of iteration, particles unswervingly update their own speed and location through individual pole value $p_{i}$ and global value $G$ in order to realize particle optimization. The update formula is as follows:

$$ V_{i} = \omega \, * \,V_{i} + c_{1} \, * \,Rand\, * \,\left( {p_{i} - X_{i} } \right) + c_{2} \, * \,Rand\, * \,\left( {G - X_{i} } \right) $$

(9)

$$ X_{i + 1} = X_{i} + V_{i} $$

(10)

Rand is a random number in $\left( {0,1} \right)$; $\omega$ is inertia coefficient. The bigger $\omega$ is, the stronger the global searching ability of the algorithm is; the smaller $\omega$ is, the stronger the local searching ability is; $c_{1}$ and $c_{2}$ are learning parameters.

Firefly algorithm [12] simulates the actions of firefly groups. It has better rate and precision of convergence, and is easier for projects to realize. The rules of firefly algorithm are as follows: (1) The firefly will be attracted to move towards those brighter ones regardless of gender factors. (2) The attractive force of fireflies is in direct proportion to their brightness. Taking two fireflies in random, one will fly toward the other which is brighter than itself, and the brightness will turn down steadily as the distance increases. (3) If there are no other brighter fireflies, the firefly will move randomly. Major parameters of firefly algorithm are as follows:

Major steps of FA are as follows:

• (1) Calculate the relative fluorescence brightness of fireflies:

$$ I = I_{0} \, * \,e^{{ - \gamma r_{ij} }} $$

(11)

$I_{0}$ represents the maximum fluorescence brightness of fireflies $i$ and $j$ is relevant to objective function value; the higher the objectivity function value is, the brighter the firefly is $\gamma$ represents the light absorption coefficient, Fluorescence will be weakened steadily with the increase of distance and absorption of spread medium; $r_{ij}$ represents the spacial distance between firefly $i$ and $j$.

• (2) Firefly attractiveness is:

$$ \beta = \beta_{0} \, * \,e^{{ - \gamma r_{ij}^{2} }} $$

(12)

$\beta_{0}$ represents the maximum attractiveness.

• (3) The update formula of location is:

$$ x_{i} = x_{i} + \beta \, * \,\left( {x_{j} - x_{i} } \right) + \alpha \, * \,\left( {Rand - \frac{1}{2}} \right) $$

(13)

$x_{i} ,x_{j}$ are the spacial location of firefly $i$ and $j$; $\alpha$ represents step size, value in $\left[ {0,1} \right]$; Rand means the random figures complying with uniform distribution within $\left[ {0,1} \right]$.

3.2 Particle Swarm Optimization Firefly Algorithm-PF Algorithm

Standard particle filter adopts method of re-sampling to prevent particle weight degeneracy, which eliminates particles with lower weights and duplicates those with higher weights. The advantage of this method lies in its easy operation. However, after several iterations, the diversity of particles will be reduced. The characteristics of firefly algorithm should be utilized at this time. Firstly, the weight of particles is compared as the fluorescent brightness of fireflies. By imagining the method of firefly optimization, low weight particles will move towards the location of high weights instead of abandoning low weight particles. Theoretically, after several times of movement, all particles will gather at the location of the particle of the highest weight, thus realizing final optimization. This process can not only maintain the location of high weight particles, make the particle groups distribute better, but also keep particle diversity.

In order to realize this process, firstly we should refer to the particle swam algorithm and guide the particle swarm by utilizing optimal value. Then location update formula and brightness formula of firefly algorithm should be improved to avoid interactive operation of particles and reduce complexity. Take the best weight as the comparison object of all the particles, then find the individual with the highest lightness. So we come up with a simplified formula $I = abs\left( {y_{t} - \widetilde{x}_{t} } \right)$, the best value is

$$ G = \left\{ {\left. {x_{t}^{n} } \right|\hbox{min} \left[ {I\left( {x_{t}^{1} } \right),I\left( {x_{t}^{2} } \right), \ldots ,I\left( {x_{t}^{N} } \right)} \right]} \right\} $$

(14)

Detailed realization and steps of the algorithm are as follows:

• Step 1. Initializing particles. Take N particles and generate particle assembly $\left\{ {x_{0}^{i} ,i = 1,2, \ldots ,N} \right\}$, Importance function is

  $$ q\left( {\left. {\tilde{x}_{t} } \right|x_{t - 1} ,y_{1:t} } \right) = p\left( {\left. {\tilde{x}_{t} } \right|x_{t - 1} } \right) $$

  (15)

• Step 2. Eliminate particles of false weight in order to cooperate with firefly algorithm to track the objectives faster and more accurate.

  When $x_{t}^{i} \, * \,\tilde{x}_{t}^{i} \, < \,0$, weight should be zero, $w_{t}^{i} = 0$ on the contrary, weight maintains the same and then normalize particle weight.

  $$ w_{t}^{i} = w_{t}^{i} /\sum\nolimits_{i = 1}^{N} {w_{t}^{i} } $$

  (16)

• Step 3. Calculate the attractiveness degree between particle i and global optimum $\beta = \beta_{0} \, * \,e^{{ - \gamma r_{i}^{2} }}$, $r_{i}$ is the distance between i and G.

• Step 4. Update the location of particles

  $$ x_{i} = x_{i} + \beta \, * \,\left( {x_{j} - x_{i} } \right) + \alpha \, * \,\left( {Rand - \frac{1}{2}} \right) $$

  (17)

• Step 5. Update global optimum $G = \left\{ {\left. {x_{t}^{n} } \right|\hbox{min} \left[ {I\left( {x_{t}^{1} } \right),I\left( {x_{t}^{2} } \right), \ldots ,I\left( {x_{t}^{N} } \right)} \right]} \right\}$

• Step 6. Set iteration termination threshold

  When $I\, > \,0.01$, do not calculate Step 4.

  When $I\, < \,0.01$, calculate Step 4 until the iteration times reach the highest.

• Step 7. Update weight. As firefly algorithm changes the spacial locations of each particle after an iteration. Therefore, while updating the location of particles, particle weights should also be updated. Detailed methods are as follows:

  $$ w_{t}^{i} = \frac{{p\left( {\left. {y_{t}^{i} } \right|\tilde{x}_{t}^{i} } \right)p\left( {\left. {\tilde{x}_{t}^{i} } \right|y_{1:t - 1} } \right)}}{{q\left( {\tilde{x}_{t}^{i} } \right)}} $$

  (18)

• Step 8. Normalization.

  $$ w_{t}^{i} = w_{t}^{i} /\sum\nolimits_{i = 1}^{N} {w_{t}^{i} } $$

  (19)

• Step 9. Output.

  $$ \tilde{x}_{t} = \sum\nolimits_{i = 1}^{N} {\tilde{x}_{t}^{i} w_{t}^{i} } $$

  (20)

From the above, we could see that through Step 2, the quality of the whole particle swarm could be improved; resources can be avoided from wasting; real-time aspects can be better promoted. As the firefly algorithm has strong convergence ability, it could make the particle swarms move toward the true range; high weight particles will further move to optimal value. This could greatly promotes the estimation accuracy of particle swarms and meanwhile, increase efficiency by setting number of iterations and avoid wasting calculating resources on those already optimized particles. Avoiding low weight particles getting into the process of iteration by setting termination threshold can help maintain particle diversity and promote algorithm real-time qualities. The algorithm fully utilizes the optimized information in the entire particle swarm, avoids interactive operation among each individuals, greatly increases the speed of operation and is conducive for particles to get rid of local extremum.

4 Simulation Experiment

This paper adopts a basic and common model (UNGM model) to check the effectiveness of the algorithm and compare it with standard particle filter algorithm and particle swarm optimized particle filter algorithm. The experimental environment is inter core2 processor with 4G internal storage and matlab2014a softwares.

The systematic state transfer model is:

$$ x_{t} = \frac{1}{2}x_{t - 1} + \frac{{25x_{t - 1} }}{{1 + x_{t - 1}^{2} }} + 8 \cos \frac{{6\left( {t - 1} \right)}}{5} + u_{t} $$

(21)

The observation model is:

$$ y_{t} = \frac{{x_{t}^{2} }}{20} + n_{t} $$

(22)

Root-mean-square error formula is:

$$ RMSE = \mathop {\left[ {\frac{1}{T}\sum\nolimits_{t = 1}^{T} {\left( {x_{t} - \tilde{x}_{t} } \right)^{2} } } \right]}\nolimits^{{\frac{1}{2}}} $$

(23)

t stands for time, $x_{t}$ stands for quantity of state, $y_{t}$ stands for quantity of observation, $u_{t}$, $n_{t}$ stands for zero-mean Guassian noise. Particle filter step is set as 50. Quantity of particles is 100. According to the universal parameters set by present references [13], maximum attractiveness degree in firefly algorithm is set as 0.9, step index 0.4, light intensity absorption coefficient 1. Generally speaking, the bigger the step index is, the stronger the global optimization ability is, but it will affect convergence precision. Otherwise, the smaller the step index is, the stronger the local optimization ability is, but it will affect convergence speed. This should be adjusted according to specific circumstances and applications (Chart 1).

Chart 1 Experimental result

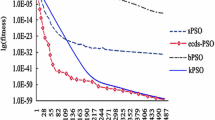
As shown in Figs. 1 and 2, PSOFA-PF algorithm is better than the other two algorithms in accuracy while tracking particle. The estimated value based on Firefly algorithm has smaller error fluctuation than the other two, which means the improved algorithm possesses not only higher accuracy, but also better stability. Compared in terms of time, it uses less than PSO-PF and keeps nearly the same as basic particle filter.

Fig. 1

Filter state estimation

Fig. 2

Absolute error

To test the diversity of samples, filter step is set to 100 in order to compare particle distribution circumstances while the time of the filter is 45 and 90. From Figs. 3 and 4, at the later period of filtering by basic particle filter, particles are mainly concentrated on minority state value and lack diversity, which is not beneficial for state estimation. While in PSOFA-PF, not only state estimation can be processed precisely, but particle diversity can also be greatly maintained.

Fig. 3

Particle distribution when t = 45

Fig. 4

Particle distribution when t = 90

5 Conclusion

To the problem of particle degeneration and loss of particle diversity in particle filter algorithm, this paper proposes an improved particle filter algorithm based on PSOFA Optimizing particle states by utilizing location update formula in firefly algorithm can avoid the process of re-sampling, make the particles possess better posterior probability distribution, promote the estimation accuracy of particle filter and guarantee particle diversity greatly. Experimental results have shown that improved algorithm distinctly enhances the overall performance of particle filter.